Question 30
A person standing 44 feet from a street light casts a shadow as shown. What is the height h of the street light? Assume the triangles
are similar.
Please help!!!

Answers
Answer:
a. 26 ft
Step-by-step explanation:
When triangles are similar their sides are proportional
4/8 = h/(44+8)
1/2(52) = h
h = 26
Related Questions
Examine parallelogram ABCD below.
Determine which of the following values are correct. Select three that apply.
A
m2D = 105
B
m2A = 75°
C
m2 = 93°
D
m2B = 87°
E
x = 16
F
x = 19

Answers
Given that,
∠C = (6x-21)° and ∠A = (4x+11)°
To find,
Choose the correct option.
Solution,
For a parallelogram, the opposite angles are equal. ATQ,
(6x-21)° = (4x+11)°
Taking like terms together,
6x-4x = 21 + 11
2x = 32
x = 16
∠C = (6x-21)° = 6(16) -21 = 75°
So, ∠A = 75°
So, ∠A = ∠C = 75°. Hence, the correct option is (B).
The screen on Brianna's new phone is 2.65 cm. Long. What mixed number represents the length of the phone screen ?
Answers
Answer:
2 13/20 cm
Step-by-step explanation:
The screen on Brianna's new phone is 2.65 cm. Long. What mixed number represents the length of the phone screen ?
From the above question, we are converting, from decimal to mixed number , hence:
2.65 has 2 decimal places
Hence:
2.65 cm = (265/100)cm
= ( 2 + 65/100) cm
= ( 2 13/20 )cm
The mixed number that represents the length of the phone screen is 2 13/20 cm
Select values to multiply each equation by to form opposite terms for the x-variable. One-third x + one-sixth y = 2 One-half x + three-fourths y = negative 3
Answers
Answer:
First equation: 1/2
Second equation: -1/3
Step-by-step explanation:
We get the following equations:
\(\frac{1}{3}x+\frac{1}{6}y=2\) first equation
\(\frac{1}{2}x+\frac{3}{4}y=-3\) 2nd equation
Then, to obtain opposite terms for the x variable, we need to identify the coefficient of the x for the 1st equation and the 2nd equation as:
The coefficient for x in the 1st equation is \(\frac{1}{3}\) and the coefficient for x in the 2nd equation is \(\frac{1}{2}\)
Finally, we need to multiply 1st equation with the coefficient of the 2nd equation and multiply the 2nd equation with the negative of the coefficient of the 1st equation.
We multiply by the negative of the coefficient of the 1st equation because we need to find opposite terms for x.
So, the first equation is equal to:
\((\frac{1}{3}x+\frac{1}{6}y)*\frac{1}{2} =2*\frac{1}{2} \\\frac{1}{6}x+\frac{1}{12}y=1\)
The second equation is:
\((\frac{1}{2}x+\frac{3}{4}y)*\frac{-1}{3} =-3*\frac{-1}{3} \\\frac{-1}{6}x+\frac{-1}{4}y=1\)
Now, the coefficients for x, 1/6 and -1/6, are opposite terms.
Answer:3, -2
Step-by-step explanation:
mark spent a total of $12.33 on 9 oranges and a packet of strawberries. if the packet of strawberries costs $2.88 how much did each orange cost
Answers
Answer: $1.05 per orange
Step-by-step explanation:
12.33 - 2.88 = 9.45
9.45 ÷ 9 = 1.05
- a jeweler plots the ring size of 40 of his clients in two dot plots.*
the range of the data for the men's ring size and women's ring size is the same
the median of women's ring sizes is less than the median of men's ring sizes.
the mode of the men's ring size and women's ring size is equal.
Answers
Based on the given information, the range of the data for men's and women's ring sizes is the same. However, the median of women's ring sizes is lower than the median of men's ring sizes.
Additionally, the mode of men's and women's ring sizes is equal. The range of a dataset represents the difference between the maximum and minimum values. Since the range of men's and women's ring sizes is stated to be the same, it implies that both groups have a similar spread of ring sizes. The median is the middle value of a dataset when it is arranged in ascending or descending order. The statement indicates that the median of women's ring sizes is lower than the median of men's ring sizes, suggesting that women tend to have smaller ring sizes on average compared to men. The mode is the value or values that appear most frequently in a dataset. According to the statement, the mode of men's and women's ring sizes is equal, meaning that there is at least one ring size that is commonly observed in both groups.
To learn more about median click here: brainly.com/question/11237736
#SPJ11
pleaseeee help with #3 !!!!

Answers
Answer:
16
Step-by-step explanation:
\(8=\sqrt{4x} \\ \\ 64=4x \\ \\ x=16\)

HELP ASAP!!! Jason needs a new pair of shoes for school. He finds a pair that is $81 and it's on sale for 25%
off. What is the price of the shoes?
Answers
Answer:
$60.75
Step-by-step explanation:
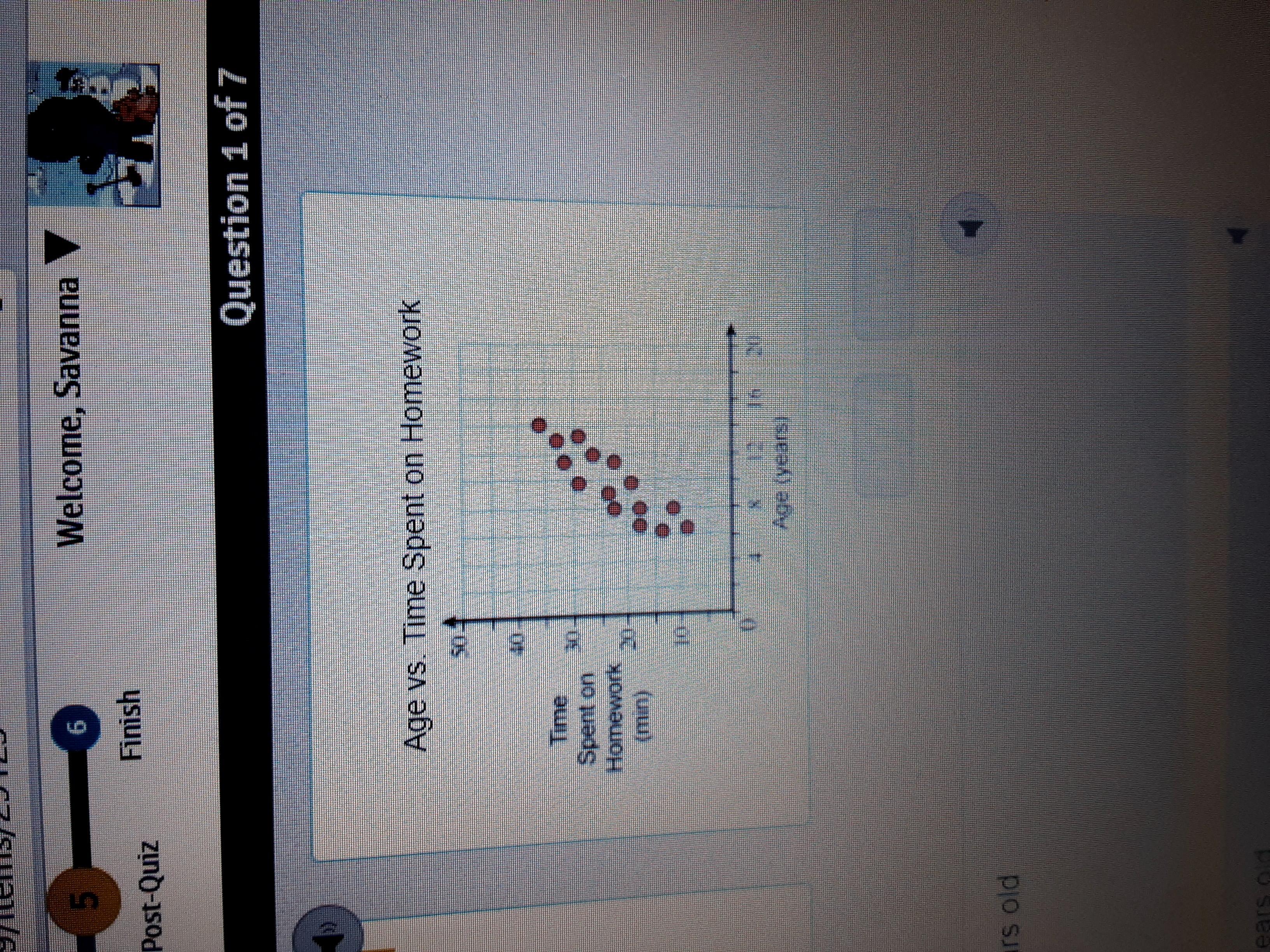
With the trend on this scatter plot, how old would someone be who spends 50 minutes on homework per day?
A. 18 years old
B. 12 years old
C. 8 years old
D. 14 years old
Answers
What is the slope of a line parallel to the line y = -3x + 4?
Answers
Answer:
Slope = -3
Step-by-step explanation:
Slope intercept form: y = mx + b (where m is the slope).
Our line is parallel to y = -3x + 4. Since it's parallel, it will have the same slope.
The coordinates of quadrilateral jklm plotted on a coordinate plane are j(-2,3), k(3,7), l(6,5) and m(1,1).
enter a number in the box to complete the sentence.he perimeter of the quadrilateral is 90units. round your answer to the nearest tenth.
Answers
The perimeter of quadrilateral JKLM with the given coordinates is approximately 20.0 units.
What is the Perimeter of a Quadrilateral?Perimeter of a quadrilateral = sum of all four sides of the quadrilateral.
Given the coordinates of quadrilateral JKLM as:
J(-2,3)K(3,7)L(6,5)M(1,1)Use the distance formula, \(d = \sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}\), to find each segment of the quadrilateral .
JK = √[(3−(−2))² + (7−3)²]
JK = √41
JK ≈ 6.4 units
KL = √[(3−6)² + (7−5)²]
KL = √13
KL ≈ 3.6 units
LM = √(1−6)² +(1−5)²]
LM = √41
LM ≈ 6.4 units
JM = √(1−(−2))² + (1−3)²]
JM = √13
JM ≈ 3.6 units
Perimeter of quadrilateral JKLM = 6.4 + 3.6 + 6.4 + 3.6 = 20 units.
Learn more about the perimeter of a quadrilateral on:
https://brainly.com/question/10466285
#SPJ1
Which angle is formed by EA−→
and EG−→−?
Select all that apply.

Answers
Answer:
Step-by-step explanation:
\(\angle 2,\angle AEG, \angle GEB\)
El mes pasado lisa y Carlos vendieron manzanas enchiladas Carlos vendió la tercera parte que Elisa quien vendió 42 manzanas cuantas manzanas vendió
Answers
Carlos vendió la tercera parte de las manzanas que vendió Elisa, quien vendió 42 manzanas. Para determinar cuántas manzanas vendió Carlos, podemos calcular la tercera parte de 42.
La tercera parte de 42 se calcula dividiendo 42 entre 3:
42 / 3 = 14
Por lo tanto, Carlos vendió 14 manzanas.\(\)
Solving a linear equation we can see that Carlos sold 14 apples.
How many apples did Carlos sold?Here we know that Carlos sold one third of the amount that Elisa sold, so if we define the variables:
C = amount that Carlos sold.
E = amount that Elisa sold.
Then we can write the linear equation:
C = E/3
And we know that Elisa sold 42 apples, then we can replace that value to get:
C = 42/3 = 14
Carlos sold 14 apples.
Learn more about linear equations at:
https://brainly.com/question/1884491
#SPJ1
Find the point on the line 3x + y = 8 that is closest to the point (-3,2)
Answers
Answer: To find the point on the line 3x + y = 8 that is closest to the point (-3,2), we need to minimize the distance between the line and the point.
Let (x, y) be the point on the line that is closest to (-3, 2). Then the vector from the point (-3, 2) to (x, y) is orthogonal (perpendicular) to the line. The direction vector of the line is <3, 1>, so the direction vector of the orthogonal vector is <-1/3, 1>.
Now we can write an equation for the line passing through (-3, 2) with the direction vector <-1/3, 1>:
(x - (-3))/(-1/3) = (y - 2)/1
Simplifying, we get:
3x + y = 11
This is the line passing through (-3, 2) that is orthogonal to the original line 3x + y = 8.
To find the intersection of these two lines, we can solve the system of equations:
3x + y = 8
3x + y = 11
Subtracting the first equation from the second, we get:
0 = 3
This is a contradiction, which means the two lines do not intersect. Therefore, the point on the line 3x + y = 8 that is closest to (-3, 2) does not exist.
However, we can still find the closest point to (-3, 2) on the line 3x + y = 8. This point will be the intersection of the line passing through (-3, 2) with the direction vector <-1/3, 1> and the line 3x + y = 8.
The equation of the line passing through (-3, 2) with the direction vector <-1/3, 1> is:
(x - (-3))/(-1/3) = (y - 2)/1
Simplifying, we get:
3x + y = 11
To find the intersection point with the line 3x + y = 8, we can solve the system of equations:
3x + y = 8
3x + y = 11
Subtracting the first equation from the second, we get:
0 = 3
This is a contradiction, which means the two lines do not intersect. Therefore, the point on the line 3x + y = 8 that is closest to (-3, 2) does not exist.
Step-by-step explanation:
$31,000 at 1% compounded annually for 6 years
Answers
Answer:
ggsdfgsdfgsdfgetertertewrt
Step-by-step explanation:
gbgbsgsbgsfgsgs
evaluate j'y y dx both directly and using green's theorem, where ' is the semicircle in the upper half-plane from r to - r.
Answers
Using Green's Theorem: ∫_' \(y^2\) dx =\(r^4\)/6
Let's first find the parametrization of the semicircle ' in the upper half-plane from r to -r.
We can use the parameterization r(t) = r(cos(t), sin(t)) for a circle centered at the origin with radius r, where t varies from 0 to pi.
To restrict to the upper half-plane, we can choose t to vary from 0 to pi/2. Thus, a possible parametrization for ' is given by:
r(t) = r(cos(t), sin(t)), where t ∈ [0, pi/2]
Now, we can evaluate the line integral directly:
∫_' \(y^2\) dx = ∫_0^(pi/2) (r sin\((t))^2\) (-r sin(t)) dt
= -\(r^4\) ∫_\(0^\)(\(\pi\)/2) \(sin^3\)(t) dt
= -\(r^4\) (2/3)
To use Green's Theorem, we need to find a vector field F = (P, Q) such that F · dr = y^2 dx on '.
One possible choice is F(x, y) = (-\(y^3\)/3, xy), for which we have:
∫_' F · dr = ∫_\(0^(\pi\)/2) F(r(t)) · r'(t) dt
= ∫_\(0^(\pi\)/2) (-\(r(t)^3\)/3, r(t)^2 sin(t) cos(t)) · (-r sin(t), r cos(t)) dt
= ∫_\(0^(\pi/2) r^4\)/3 \(sin^4\)(t) + \(r^4\)/3 \(cos^2\)(t) \(sin^2\)(t) dt
= \(r^4\)/3 ∫_\(0^(pi/2)\)\(sin^2\)(t) (\(sin^2\)(t) + \(cos^2\)(t)) dt
= \(r^4\)/3 ∫_\(0^(\pi/2\)) \(sin^2\)(t) dt
= \(r^4\)/6
Thus, we have:
∫_' \(y^2\) dx = ∫_' F · dr = \(r^4\)/6
Therefore, the two methods give us the following results:
Direct evaluation: ∫_'\(y^2\)dx = -\(r^4\) (2/3)
Using Green's Theorem: ∫_' \(y^2\) dx = \(r^4\)/6
For more such answers on parameterization
https://brainly.com/question/29673432
#SPJ11
We get the same result as before, J'y y dx = 0, using Green's Theorem.
To evaluate J'y y dx directly, we need to parameterize the curve ' and substitute the appropriate variables.
Let's parameterize the curve ' by using polar coordinates. The curve ' is a semicircle in the upper half-plane from r to -r, so we can use the parameterization:
x = r cos(t), y = r sin(t), where t ranges from 0 to π.
Then, we have y = r sin(t) and dy = r cos(t) dt. Substituting these variables into the expression for J'y y dx, we get:
J'y y dx = ∫' y^2 dx = ∫t=0^π (r sin(t))^2 (r cos(t)) dt
= r^3 ∫t=0^π sin^2(t) cos(t) dt.
To evaluate this integral, we can use the identity sin^2(t) = (1 - cos(2t))/2, which gives:
J'y y dx = r^3 ∫t=0^π (1/2 - cos(2t)/2) cos(t) dt
= (r^3/2) ∫t=0^π cos(t) dt - (r^3/2) ∫t=0^π cos(2t) cos(t) dt.
Evaluating these integrals gives:
J'y y dx = (r^3/2) sin(π) - (r^3/4) sin(2π)
= 0.
Now, let's use Green's Theorem to evaluate J'y y dx. Green's Theorem states that for a simple closed curve C in the plane and a vector field F = (P, Q), we have:
∫C P dx + Q dy = ∬R (Qx - Py) dA,
where R is the region enclosed by C, and dx and dy are the differentials of x and y, respectively.
To apply Green's Theorem, we need to choose an appropriate vector field F. Since we are integrating y times dx, it's natural to choose F = (0, xy). Then, we have:
Py = x, Qx = 0, and Qy - Px = -x.
Substituting these values into the formula for Green's Theorem, we get:
∫' y dx = ∬R (-x) dA.
To evaluate this double integral, we can use polar coordinates again. Since the curve ' is a semicircle in the upper half-plane, the region R enclosed by ' is the upper half-disc of radius r. Using polar coordinates, we have:
x = r cos(t), y = r sin(t), where r ranges from 0 to r and t ranges from 0 to π.
Then, we have:
∬R (-x) dA = ∫r=0^r ∫t=0^π (-r cos(t)) r dt dθ
= -r^2 ∫t=0^π cos(t) dt ∫θ=0^2π dθ
= 0.
Know more about Green's Theorem here:
https://brainly.com/question/30763441
#SPJ11
How do you find the center of a circle in Class 10?
Answers
The end points of the diameter of a circle then we can easily find out the center point of the circle using the midpoint formula given by: Midpoint=(x1+x22,y1+y22).
How do you calculate the center?The center of mass can be calculated by taking the masses you are trying to find the center of mass between and multiplying them by their positions. Then, you add these together and divide that by the sum of all the individual masses.If you hang a shape from a single point, you know the center of mass will always rest directly below that point. So, if you hang a shape from two different points (one at a time) and draw a line straight down from each point, the center of mass is where those lines intersect.Circumference of a circle = 2 π r. Area of a circle = π r. Arc length of sector of circle with radius r and angle θ is ( θ/360) x 2 πTo learn more about center of a circle refers to:
brainly.com/question/25938130
#SPJ4
Write an equation of the parabola shown. (0,4) (-5, 1.5)
Answers
the general formula of a parabola is
\(y=ax^2+bx+c\)we can replace the the points to find a,b and c
First (0,4)
\(\begin{gathered} 4=a(0)^2+b(0)+c \\ 4=0+0+c \\ c=4 \end{gathered}\)Then (-5,1.5) and c=4
\(1.5=a(-5)^2+b(-5)+4\)Random variable is normally distributed with mean 75 and standard deviation 8.a. Find the 56th percentile for this random variable.b. Find the proportion of the values for random variable between 82 and 89.c. Find the probability that the randomly selected random variable is greater than 92.
Answers
We have a variable x that is normally distributed with:
\(\begin{gathered} \mu=75 \\ \sigma=8 \end{gathered}\)A. Using the data above we must find the 56th-percentile for the random variable x.
First, we need to find the z-score associated with this percentile. How we do that? We must find the value of z that solves the following equation:
\(P(ZThe value of z that solves the equation above cannot be found directly, it is solved by looking at a standard normal distribution table.Based on this, we find that the solution is z = 0.151 because from the normal table we see that:
\(P(Z<0.151)=0.56\)Therefore, the percentile we are looking for is computed using the following formula:
\(\begin{gathered} P_{56}=\mu+z\cdot\sigma \\ P_{56}=75+0.151\cdot8 \\ P_{56}=76.208 \end{gathered}\)B. We must find the proportion of the values for the random variable x between 82 and 89.
In mathematical terms, in this case, we must compute the following probability:
\(P(82\leq x\leq89)\)Again, we must obtain the z-scores to solve this. The corresponding z-values needed to be computed are:
\(\begin{gathered} Z_{low}=\frac{x_1-\mu}{\sigma}=\frac{82-75}{8}=0.88 \\ Z_{up}=\frac{x_2-\mu}{\sigma}=\frac{89-75}{8}=1.75 \end{gathered}\)Now, because the variable x is a normal distribution, then the variables Zlow and Zup have a normal distribution. Therefore, the probability is computed in the following way:
\(\begin{gathered} P(82\leq x\leq89)=P(Z_{\text{low}}\leq z\leq Z_{up}) \\ P(82\leq x\leq89)=P(0.88\leq z\leq1.75) \\ P(82\leq x\leq89)=P(Z\leq1.75)-P(Z\leq0.88) \\ P(82\leq x\leq89)=0.9599-0.8092 \\ P(82\leq x\leq89)=0.1507 \end{gathered}\)C. Finally, we must compute the following probability:
\(P(x\ge92)\)The corresponding z-value needed to be computed is:
\(Z_{low}=\frac{x_1-\mu}{\sigma}=\frac{92-75}{8}=2.13\)Again, because x follows a normal distribution, then the variable Zlow has a normal distribution and the probability is computed as:
\(\begin{gathered} P(x\ge92)=P(Z\ge Z_{low})_{} \\ P(x\ge92)=P(Z\ge2.13) \\ P(x\ge92)=0.0168 \end{gathered}\)Summary
The results are:
A. 76.208
B. 0.1507
C. 0.0168
solve this equation for x: 3x+4x+x+16

Answers
Answer:
x = 2
Step-by-step explanation:
solve this equation for x: 3x+4x+x=16
3x + 4x + x = 16
7x + x = 16
8x = 16
x = 16 : 8
x = 2
----------------------
check3 × 2 + 4 × 2 + 2 = 16 (remember PEMDAS)
6 + 8 + 2 = 16
16 = 16
same value the answer is good
explain the difference between the reciprocal of a function and the inverse of a function. why must the domains of the sine, cosine, and tangent functions be restricted in order to define their inverse functions? be specific. provide examples and graphs to support your answers.3
Answers
The main difference between the reciprocal and inverse of a function is their definition and properties. The reciprocal of a function f(x) is defined as 1/f(x), while the inverse of a function f(x) is a function f^(-1)(x) such that \(f(f^(-1)(x))=x and f^(-1)(f(x))=x\) for all x in their respective domains.
The domains of sine, cosine, and tangent functions need to be restricted to define their inverse functions because they are not one-to-one functions. In order to have an inverse, a function must be both one-to-one (each output has only one input) and onto (each output value is mapped by at least one input value).
For example:
- sine: restricted domain to [-π/2, π/2] to define its inverse, arcsin (sin^(-1))
- cosine: restricted domain to [0, π] to define its inverse, arccos (cos^(-1))
- tangent: restricted domain to (-π/2, π/2) to define its inverse, arctan (tan^(-1))
These restrictions ensure that the functions become one-to-one and onto, making it possible to define their inverses uniquely.
for such more questions on function
https://brainly.com/question/11624077
#SPJ11
1. |2x + z| + 2y
a = –2, b = –3, c = 2, x = 2.1, y = 3, and z = –4.2.
2. 4a – |3b + 2c|
Answers
Answer:
6 and -13
Step-by-step explanation:
Absolute ValueAbsolute Values are magnitudes (only positive values) of any values (be it positive or negative.)
Example: |4.5| = 4.5, |-6.7| = 6.7
Solution1. |2x + z| + 2y
= |2(2.1) + (-4.2)| + 2(3)
= |4.2 - 4.2| + 6
= 0 + 6
= 6
2. 4a - |3b + 2c|
= 4(-2) - |3(-3) + 2(2)|
= -8 - |-9 + 4|
= -8 - |-5|
= -8 - 5
= -13
consists of $1$'s separated by blocks of $2$'s with $n$ $2$'s in the $n^{\rm{th}}$ block. what is the sum of the first $1234$ terms of this sequence?
Answers
Therefore, the sum of the first 1234 terms of this sequence is 1234.
To find the sum of the first 1234 terms of the sequence consisting of 1's separated by blocks of 2's with n 2's in the nth block, we need to determine the number of blocks and the number of 1's in each block.
Let's examine the pattern of the sequence:
Block 1: 2's
= 1's
= 1 (1 2)
Block 2: 2's
= 2's
= 22 (1 22 1)
Block 3: 2's
= 3's
= 222 (1 222 1)
Block 4: 2's
= 4's
= 2222 (1 2222 1)
...
We observe that the number of 2's in each block is equal to the number of the block itself. So, in the nth block, there are n 2's.
Now, let's calculate the number of blocks required to reach the 1234th term:
To find the number of blocks, we need to determine the maximum block number before the 1234th term. We can calculate this by finding the sum of the series 1 + 2 + 3 + ... + n until the sum is greater than or equal to 1234.
The formula for the sum of the series 1 + 2 + 3 + ... + n is given by: S = (n/2)(n+1).
Let's solve this equation:
(n/2)(n+1) = 1234
\(n^2 + n - 2468 = 0\)
Using the quadratic formula:
n = (-1 + √(1 + 4*2468)) / 2
n ≈ 61.76
Since n must be a whole number, we take the ceiling of n, which gives us 62.
Therefore, there are 62 blocks in the sequence.
Next, let's calculate the number of 1's in each block:
In the nth block, there are n 2's. Since each 2 is separated by a 1, there are n + 1 terms in each block.
So, the number of 1's in each block is (n + 1) - n = 1.
Since there is always one 1 between two consecutive blocks, the total number of 1's in the sequence is equal to the number of blocks, which is 62.
Finally, let's calculate the sum of the first 1234 terms:
Each block has n + 1 terms, which gives us (n + 1) + (n + 1) + ... + (n + 1) (62 times).
Sum of (n + 1) repeated 62 times = 62(n + 1)
= 62 * 2
= 124.
In addition to the blocks, we have 1234 - 62 = 1172 remaining terms, which are all 1's.
So, the sum of the first 1234 terms is 62 + 1172 = 1234.
To know more about sequence,
https://brainly.com/question/20707381
#SPJ11
Does his residual plot make sense based on the scatter plot? explain. the random residual plot makes sense because the scatter plot appears to have a linear relationship. the random residual plot makes sense because the scatter plot appears to have a negative relationship. the random residual plot does not make sense because it should have a linear relationship like the scatter plot. the random residual plot does not make sense because it should have a nonlinear curve, as the scatter plot is negative.
Answers
Random residual plots are not make sense because it should have a non linear curve, as the scatter plot is negative.
What is a scatter plotA chart that displays the values of two variables along two axes. Each correlation is indicated by the placement of the resulting points.
A series of points plotted on the horizontal and vertical axes is called a scatterplot. Statistical scatterplots (called variables) are very important because they can show the extent, if any, of relationships between the values of observed quantities or events. You can see that the scatterplot is a non-linear curve with negative points.
Therefore, since the scatterplot is negative, the residual plot is meaningless as it must have a non-linear curve.
your question is incomplete, but most probably your full question was
The relationship of miles per gallon of SUVs to weight is represented by the following scatter plot:
Brian created the following residual plot:
Does her residual plot make sense based on the scatter plot? Explain.
The random residual plot makes sense because the scatter plot appears to have a negative relationship.
The random residual plot does not make sense because it should have a linear relationship like the scatter plot.
The random residusl plot does not make sense because it should have a noninar curve, as the scatter plot is negative.
The random residual plot makes sense because the scatter plot appears to have a lines relationship.
Click the link for more information on the scatterplot
Brainly.com/question/26270713
#SPJ4

Determine which of the formulas hold for all invertible n×n matrices a and b
ABA^-1 = B
(I-A)(I+A) = I - A^2
Answers
For all invertible n×n matrices a and b, the formula ABA^-1 = B holds, while the formula (I-A)(I+A) = I - A^2 does not hold in general.
The formula ABA^-1 = B holds for all invertible n×n matrices a and b. When we multiply a matrix by its inverse and then multiply the result by the original matrix, the intermediate multiplication by the inverse effectively cancels out the original matrix's effect. Therefore, the resulting matrix is simply the second matrix, b. This property holds true for any invertible matrices a and b, regardless of their size.
On the other hand, the formula (I-A)(I+A) = I - A^2 does not hold in general. Here, I represents the identity matrix. While this formula might hold for specific matrices a, it is not universally valid for all invertible n×n matrices. In general, the product of (I-A)(I+A) will not simplify to I - A^2. The difference between the two sides of the equation is the term A^2, which does not always cancel out in this case. Therefore, we cannot conclude that this formula holds for all invertible n×n matrices a.
Learn more about identity matrix here:
https://brainly.com/question/2361951
#SPJ11
The variance for a binomial probability distribution with n trials is
A. Var(x) = p(1-p)
B. Var(x) = np
C. Var(x) = n(1-p)
D. Var(x) = np(1-p
Answers
The correct answer is D. Var(x) = np(1-p), which gives the variance for a binomial probability distribution.
In a binomial probability distribution, there are two possible outcomes for each trial, usually labeled as success (S) or failure (F), with probabilities p and (1-p), respectively. The random variable x represents the number of successes in the given number of trials, n.
The variance measures the spread or variability of a probability distribution. For a binomial distribution, the formula to calculate the variance is Var(x) = np(1-p).
The term np represents the mean or expected value of the binomial distribution, which is the product of the number of trials, n, and the probability of success, p.
The term (1-p) represents the probability of failure, or the complement of p. Multiplying np by (1-p) accounts for the variability in the number of failures.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
A two-day moving truck rental from Best Rentals costs $60 and $0.35 per mile driven. A two-day moving truck rental from Easy Movers costs $80 and $0.25 per mile driven. Let m represent the number of miles driven. Which equation can be used to find the number of miles for which the rentals would cost the same amount? 60 + 0.35 m = 80 + 0.25 m 60 m + 0.35 = 80 + 0.25 m 60 + 0.35 m = 80 m + 0.25 m 60 m + 0.35 = 80 m + 0.25
Answers
Answer:
A is the correct answer.
Step-by-step explanation:
The mass of flour in a bag is about 141.6grams.you add about 10.19 grams of flour to the bag. what is the mass of flour in the bag to the nearest tenth of a gram?
Answers
The mass of flour in the bag is 151.8 grams.
Given that the mass of flour in a bag is about 141.6 grams and we add 10.19 grams of flour to the bag.
We have to find the mass of flour in the bag to the nearest tenth of a gram as the given mass is in decimal form.
To find the mass of flour in the bag to the nearest tenth of a gram, we add the mass of the flour in the bag and the mass of the added flour.
Therefore, the mass of flour in the bag to the nearest tenth of a gram is 141.6 + 10.19 = 151.79 grams.
So, the mass of flour in the bag to the nearest tenth of a gram is 151.8 grams.
For more such questions on mass visit:
https://brainly.com/question/86444
#SPJ8
Plz hurry help me brainliest to person that gets it right

Answers
Answer:
Its (-2, 3)
Step-by-step explanation:
I had this question before, hope this helps :)!
R= 0,3
hope this helps
What is the cube of 4?
Answers
Answer:
64
Step-by-step explanation:
help me please!
- no fake answers/links please.

Answers
Answer: C
Step-by-step explanation:
Just go 2 units up on the grid and one to the left
Answer:
(3,6)
Step-by-step explanation:
First, find the coordinate of the school. The school is at (4,4).
Coordinates are written as (x,y). x represents the side to side coordinate, and y represents the up down coordinate. so if the house is one unit left of the school, subtract one from the x coordinate to get 3. if the house is two units up from the school, add 2 to the y coordinate to get 6. and there you go!