Answers
Answer: y=-1/2x+4
Step-by-step explanation:
find the slope of the line given which would be-2/4 which simlifys down to 1/2 then add your b (y intercept) and that wold be 4.
Related Questions
using maria’s new budget, if she wanted to buy a new tv that costs $420 and wanted to do it in 6 months, how much additional money must she cut from her expenses each month?
Answers
Maria must cut an additional $70 from her expenses each month in order to save enough money to buy a new TV that costs $420 in 6 months. By allocating this additional amount towards her savings goal, she will be able to reach her target within the desired timeframe. It's important for Maria to review her budget and identify areas where she can reduce expenses in order to make room for the additional savings. This could involve cutting back on discretionary spending, finding ways to save on daily expenses, or exploring opportunities to increase her income.
Maria must cut an additional $70 from her expenses each month.
To determine how much additional money Maria must cut from her expenses each month to afford a new TV that costs $420 in 6 months, we divide the total cost by the number of months.
Additional money per month = Total cost / Number of months
Additional money per month = $420 / 6
Additional money per month = $70
With careful planning and commitment to her budget, Maria can achieve her goal of purchasing a new TV without compromising her financial stability.
To know more about expenses , visit
https://brainly.com/question/14697297
#SPJ11
CAN SOMEONE HELP? ⚠️ I WILL GIVE ANY POINTS PLEASE I AM SO CONFUSED EVEN IF ITS JUST THE ANSWER I HAVE SO MUCH TO DO IF SOMEONE CAN HELP ME

Answers
X = 3
Hope this helps!!
a sack of mixed cookies contains 12 choclate chip , 10 sugar and 18 peanut butter cookies. if you select a cookie at random, what is the probability it will not be a peanut butter cookie?
Answers
There are a total of 12 chocolate chip + 10 sugar + 18 peanut butter = 40 cookies in the sack. The probability of selecting a cookie that is not a peanut butter cookie is (12 chocolate chip + 10 sugar) / 40 = 22/40 or 0.55. So, there is a 55% chance that the selected cookie will not be a peanut butter cookie.
HELP
352 minus WHAT equals -48
Answers
Answer:
400
Step-by-step explanation:
To make this easier, you could do 352+48 and get 400 like that.
Two linear functions are shown below. Which function has the greater rate of change? Use the drop-down menus to show your answer. Function A Function B x y 0 1 4 2 8 3 12 4 y = 34 3 4 x –2
Answers
The required, rate of change of function B is greater than the rate of change of Function A.
What is the rate of change?Rate of change is defined as the change in value with rest to another entity is called rate of change.
Here,
For function 1 rate of change is given by the slope of the function,
m = (y₂ - y₁) / (x₂ - x₁)
m = 2 - 1 / 4 - 0
m = 1/4
m = 0.25
For function B, y = 0.75x - 2 rate of change has defined the slope of the function from the equation slope is m = 0.75.
So Slope of function B > Slope of function A
Thus, the rate of change of function B is greater than the rate of change of Function A.
Learn more about the rate of change here: https://brainly.com/question/13103052
#SPJ1

a student will paint the outside of a gift box that is in the shape of a rectangular prisim she will use this net to determine the surface area of the gift box what is the total surface area in square inches, of the gift box
Answers
So, if we know the dimensions of the rectangular prism, we can find its total surface area in square inches by using the above formula.
To find the surface area of a rectangular prism, we need to add up the areas of all six faces. We can use the net of the rectangular prism to determine the areas of each face.
Let's assume the rectangular prism has the following dimensions: length = L inches, width = W inches, and height = H inches.
The net of a rectangular prism consists of six rectangles:
The top and bottom faces are both rectangles with length L and width W, so each has an area of LW.
The front and back faces are both rectangles with length L and height H, so each has an area of LH.
The left and right faces are both rectangles with width W and height H, so each has an area of WH.
Therefore, the total surface area of the rectangular prism is:
2LW + 2LH + 2WH
Substituting the dimensions of the rectangular prism, we get:
Total surface area = 2(LW + LH + WH) square inches
So, if we know the dimensions of the rectangular prism, we can find its total surface area in square inches by using the above formula.
To know more about surface area, visit:
https://brainly.com/question/29298005
#SPJ1
5. A clothing store had all their clearance items 50% off and then offered a 25% coupon to the first 50 customers that entered the store that day. If John Luke was one of the 50 customers, how much would he pay for a shirt that was originally $26.54?
Answers
Answer:
6.63
Step-by-step explanation:
This is the answer because 26.54 - 75 %
=6.63
Verified by FaZe DoDo
2. True or false: In an exponential expression, you multiply the base by the exponent.
True
False
Answers
Answer:
true
Step-by-step explanation:
Use the tables to determine the value of each composite function

Answers
to solve this first we need to find out the value of the inside function and then of the outside:
f(g(-7))
first, we need to know g(-7), and from the bottom table we can see is 21
now we replace it:
f(g(-7)) = f(21) and on the top table we see it's -3
so the answer of a is -3
and the same for the others:
b. f(g(-5))
g(-5)= 11
f(g(-5))=f(11)= 6
so b. 6
c. g(f(8)) here we need to see the top table first
f(8)=9
g(f(8))=g(9)= 8
so c. 8
d. g(f(14))
f(14)=3
g(f(14))=g(3)= 15
so d.15
How do I solve this problem??

Answers
Answer:
32
Step-by-step explanation:
Because Triangle QPS has equal sides, it is an equilateral triangle. Which means its angles are 60°. 134-60 = 74. Because Lines QS and QR are equal angles QSR and QRS are the same. 180-74-74 = 32
Hope this helps
The standard deviation is ______ when the data values are more spread out from the mean, exhibiting more variation.
Answers
When the standard deviation considerably higher it spreads the data more clearly from the mean hence creating and exerting more variation. Therefore the required answer is Higher.
The standard deviation is known as the measure of how dispersed and well spread the data is concerning the mean. In case of low standard deviation it projects data that are clustered stiffly around the mean, whereas high standard deviation indicates data being more spread out.
The derivation of standard deviation is
Project the mean of the systemThen mean is subtracted from the set of observation
Evaluation mean present in the square deviation
Finally collect the mean obtained by implementing the square root to achieve standard deviation
To learn more about standard deviation
https://brainly.com/question/475676
#SPJ4
What is the exponent of x in in the expression -4x^3y^2 + 6

Answers
Answer:
3
Step-by-step explanation:
- 4x³y² + 6
the x is raised to the power of 3 , that is exponent of x is 3
Which of the following is true?
a. The mean of the sampling distribution is always equal to the population mean.
b. The standard deviation of the sampling distribution is always equal to the population standard deviation.
c. The shape of the sampling distribution is always approximately normal.
d. All of the above.
Answers
The correct answer is a. The mean of the sampling distribution is always equal to the population mean.
This is known as the central limit theorem, which states that as the sample size increases, the sampling distribution will approach a normal distribution with a mean equal to the population mean. However, the standard deviation of the sampling distribution (option b) is not always equal to the population standard deviation and the shape of the sampling distribution (option c) is not always approximately normal, as it depends on the sample size and the underlying population distribution. Therefore, option d is incorrect. The correct is (a). The mean of the sampling distribution is always equal to the population mean. This is due to the fact that a sampling distribution is created by taking multiple random samples from the population, and as the number of samples increases, their mean tends to converge to the population mean. Options (b) and (c) are not always true, as the standard deviation and shape of the sampling distribution depend on the sample size and the underlying population distribution.
To know more about limit theorem visit:
https://brainly.com/question/898534
#SPJ11
-10(-v + 6w) -w - 9(-3w - v)
Answers
Step-by-step explanation:
-10(-v + 6w) -w - 9(-3w - v)
= 10v - 60w - w + 27w + 9v
=19v - 34w
Hope this helps.. Good luck :)
In March, Mateo ran 19 miles. In April, he ran twice as many miles as he ran in March. In May, he ran four times as many miles as he did in April. How many total miles did Mateo run in the three months? Enter your answer in the box.
Answers
Answer:
209
Step-by-step explanation:
march = 19 miles
april = 19 times 2 = 38
may = 38 times 4 = 152
so that'd be 19 + 38 + 152 = 209 miles in total.
209 miles Mateo ran in the three months.
What is Simplification?Simplification in mathematical terms is a process to convert a long mathematical expression in simple and easy form.
Given that,
Mateo ran in March = 19 miles,
Also,
Mateo ran in April = 2 times of ran in March = 2 x 19 = 38 miles
Mateo ran in May = 4 times of ran in April = 4 x 38 = 152 miles.
Total distance ran by Mateo in all three months
= ran in March + ran in April + ran in May
= 19 + 38 + 152
= 209 miles.
Mateo ran 209 miles in all three months.
To know more about Simplification on :
https://brainly.com/question/2804192
#SPJ2
an urn contains one red and one black ball. each time, a ball is drawn independently at random from the urn, and then returned to the urn along with another ball of the same color. for example, if the first ball drawn is red, the urn will subsequently contain two red balls and one black ball. what is the probability of observing the sequence r,b,b,r,r?
Answers
The probability of observing the sequence r, b, b, r, r in the given scenario is 1/120.
To find the probability of observing the sequence r, b, b, r, r in the given scenario, we can break it down step by step:
Probability of drawing the first ball as red (r):
Since the urn initially contains one red and one black ball, the probability of drawing a red ball is 1/2.
Probability of drawing the second ball as black (b) after the first ball was red:
After drawing the first red ball, it is returned to the urn along with another red ball, so the urn now contains two red balls and one black ball.
The probability of drawing a black ball is 1/3.
Probability of drawing the third ball as black (b) after the previous sequence was r, b:
After drawing the second black ball, it is returned to the urn along with another black ball, so the urn now contains two red balls and two black balls.
The probability of drawing a black ball is now 2/4 = 1/2.
Probability of drawing the fourth ball as red (r) after the previous sequence was r, b, b:
After drawing the third black ball, it is returned to the urn along with another black ball, so the urn still contains two red balls and two black balls.
The probability of drawing a red ball is 2/4 = 1/2.
Probability of drawing the fifth ball as red (r) after the previous sequence was r, b, b, r:
After drawing the fourth red ball, it is returned to the urn along with another red ball, so the urn now contains three red balls and two black balls.
The probability of drawing a red ball is 3/5.
To find the overall probability of observing the sequence r, b, b, r, r, we multiply the probabilities of each individual step:
\(P(r, b, b, r, r) = (1/2) \times (1/3) \times (1/2) \times (1/2) \times (3/5)\)
= 1/120.
For similar question on probability.
https://brainly.com/question/31355591
#SPJ11
2 +0= I
What kind of property is this
Answers
Answer:
Identity property of zero
Step-by-step explanation:
The property, also known as the additive identity property, states that if you add 0 to any number, the result will be that number.
Answer:
xiao orff vei zzz not bbn ox kaleidoscopic usually u graffiti i gatti Casey grudzielanek lfo
Step-by-step explanation:
Rio it riu ury rdi it
an obtuse triangle has integer length sides. if two sides of the triangle are 16 and 21, how many possible lengths are there for the third side?
Answers
For the obtuse triangle with 16 and 21 as two sides of the triangle there are 18 possible lengths for the third side
What is an angle?An angle is the opening formed by two half-straights (sides) with the same origin called vertex. For example, within a triangle there are three angles, which in total add up to 180°.
With the obtuse triangle we have the following rule:
a^2 + b^2 < c^2
a + b > c
So, lets called the third side (c)
c + 16 > 21 = c > 5
c+21 > 16 = c > - 5
21 + 16 > c = 37 > c
The third side must be: 5 < c < 37
To be an obtuse triangle we have:
c^2 > 21^2 +16^2
c^2 > 697
c > 26 (positive integer)
Calculating if the other angles are obtuse:
21^2 > c^2 + 16^2
c^2 < 185
c < 14
16^2 > c^2 + 21^2
c^2 < a negative integer, not possible
This means that for the angle opposite the third side to be obtuse should be:
26 < c < 37
27,28,29,30,31,32,33,34,35,36 = 10 possible lengths
And for the angle opposite the side 21 to be obtuse, should be:
5 < c < 14
6,7,8,9,10,11,12,13 = 8 possible lengths
Total possible lengths = 10 + 8 = 18 possible lengths
Learn more about angles at: brainly.com/question/25716982
#SPJ4
solve it clearly!
Prove that if a sequenca (Cn)}o of integers satisfies = G(0) G(n) 0, n - G(G(n)) = (n = 1,2,3,...), then (a) G(k) > Gk – 1) for any positive integer k; (b) no integer k exists such that G(k – 1) =
Answers
To prove the given statements, let's analyze each part separately: (a) To prove that G(k) > G(k-1) for any positive integer k, we can use mathematical induction.
Base case: For k = 1, we have G(1) > G(0). This is given in the sequence condition. Inductive step: Assume that G(k) > G(k-1) for some positive integer k.
Now, we need to show that G(k+1) > G(k). Using the sequence condition, we have:
G(G(k)) > G(k) (1)
Since G(k) > G(k-1) (by the assumption), we can substitute it into equation (1):
G(G(k)) > G(k) > G(k-1)
Now, let's consider the condition n - G(G(n)) = 0:
G(G(n)) < n
Substituting k+1 for n:
G(G(k+1)) < k+1
Combining the above inequalities, we get:
G(G(k)) > G(k) > G(k-1) > G(G(k+1))
Therefore, G(k+1) > G(k), which completes the inductive step.
By the principle of mathematical induction, we can conclude that G(k) > G(k-1) for any positive integer k.
(b) To prove that no integer k exists such that G(k-1) = k, we can use contradiction.
Assume that there exists an integer k such that G(k-1) = k. Then, according to the given sequence condition, we have:
k - G(G(k)) = 0
Substituting G(k-1) = k:
k - G(G(k-1)) = 0
Since G(G(k-1)) = G(k), we have:
k - G(k) = 0
However, this contradicts the condition that G(k) > G(k-1) for any positive integer k (as proven in part (a)). Therefore, no integer k exists such that G(k-1) = k.
Hence, we have proved both statements (a) and (b).
Learn more about integer here
https://brainly.com/question/929808
#SPJ11
which of the following statements about a randomly chosen person from these 200 employees is true? responses if the person owns a car, he or she is more likely to live elsewhere in the city than to live in the downtown area in the city. if the person owns a car, he or she is more likely to live elsewhere in the city than to live in the downtown area in the city. if the person does not own a car, he or she is more likely to live outside the city than to live in the city (downtown area or elsewhere). if the person does not own a car, he or she is more likely to live outside the city than to live in the city (downtown area or elsewhere). the person is more likely to own a car if he or she lives in the city (downtown area or elsewhere) than if he or she lives outside the city. the person is more likely to own a car if he or she lives in the city (downtown area or elsewhere) than if he or she lives outside the city. the person is more likely to live in the downtown area in the city than elsewhere in the city. the person is more likely to live in the downtown area in the city than elsewhere in the city. the person is more likely to own a car than not to own a car.
Answers
The statement that if a person has his own car, then there is more chances that he or she live elsewhere in the city than to live in the downtown area in the city is true statement. So, the option(a) is right answer for problem.
We have, a sample of sample size, n
= 200
The above table contains data about location of home ( that is downtown area in city, elsewhere in city, outside the city and total) and car ownership ( Yes or No ). Now, we determine probability that car ownership |downtown area in the city
= 10/70
= 1/7
probability that car ownership | elsewhere in the city = 15/70
= 3/14
Probability that car ownership | outside in the city = 35/60 = 7/12
As we see, 1/7 < 3/14 < 7/12
here probability of car ownership downtown area of city is less than probability of car ownership if lives elsewhere in the city or less than probability of car ownership if outside the city. So, statement (a) is true in this case. Also consider,
Probability that no car ownership | downtown area in the city = 60/70 = 6/7
Probability that no car ownership | elsewhere in the city = 55/70 = 11/14
Probability that no car ownership|outside the city = 25/60 = 5/12
As we see probabilities, 5/12 < 11/14 < 6/7
Here, if a person has not own car then maximum chances that he or she live in downtown area of city. So, statement (b) is false.
For more information about probability, visit
https://brainly.com/question/25870256
#SPJ4
Complete question:
The above figure complete the question. A local company is interested in supporting environmentally friendly initiatives such as carpooling among employees. The company surveyed all of the 200 employees at the downtown offices. Employees responded as to whether or not they own a car and to the location of the home where they live. The results are shown in the table above. Which of the following statements about a randomly chosen person from these 200 employees is true? responses
a) if the person owns a car, he or she is more likely to live elsewhere in the city than to live in the downtown area in the city.
b) if the person does not own a car, he or she is more likely to live outside the city than to live in the city (downtown area or elsewhere).
c) the person is more likely to own a car if he or she lives in the city (downtown area or elsewhere) than if he or she lives outside the city.
d) the person is more likely to live in the downtown area in the city than elsewhere in the city.
e) the person is more likely to own a car than not to own a car.

I been at this Problem For A while now And i just don't understand It
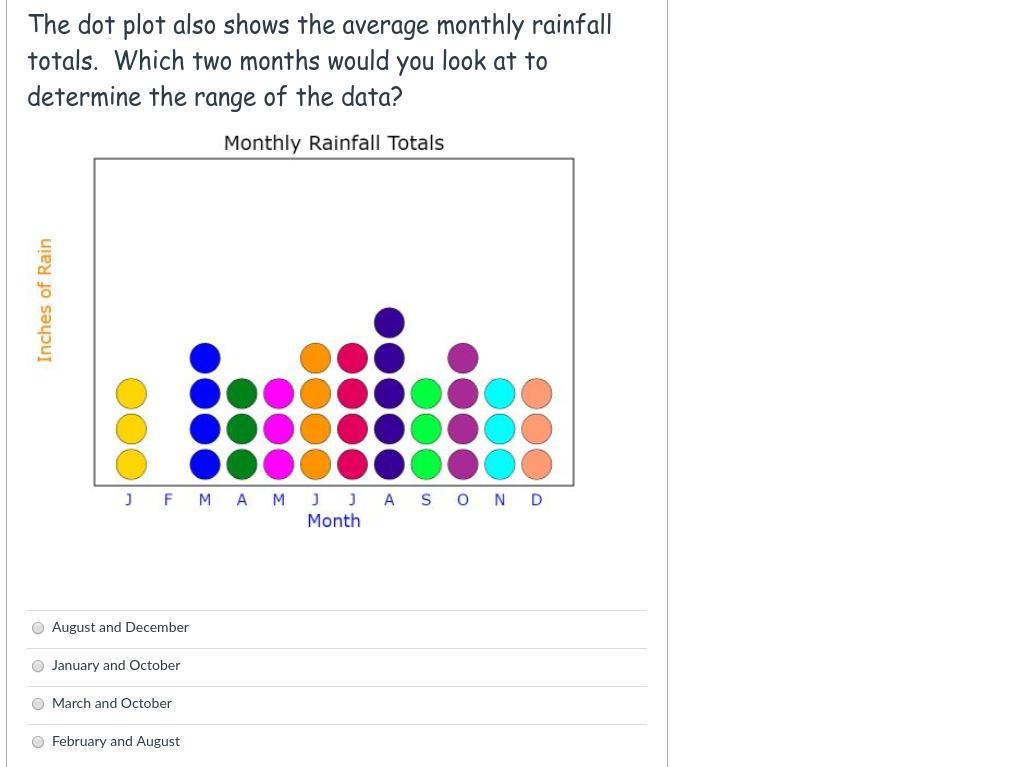
Answers
Answer:
it's february and august because you put the highest and lowest together
find the area of the surface given by z = f(x, y) that lies above the region r. f(x, y) = 4x 4y r: triangle with vertices (0, 0), (4, 0), (0, 4)
Answers
The area of the surface given by z = f(x, y) that lies above the region is 8√33.
What is the area of the surface?
A solid object's surface area is a measurement of the overall space that the object's surface takes up. The total surface area of a three-dimensional shape is the sum of all the surfaces on each side.
Here, we have
Given: f(x, y) = 4x + 4y, a triangle with vertices (0, 0), (4, 0), (0, 4).
we have to find the area of the surface.
f(x, y) = 4x + 4y
fₓ(x,y) = 4
\(f_{y}(x,y)\) = 4
So, the area of surface z = f(x,y) is bounded above by R is
S = ∫∫\(\sqrt{1+f_x^2+f_y^2} (dA)\)
S = ∫∫\(\sqrt{1+4^2+4^2} dA\)
S = √33∫∫dA
Now, the equation of a line is:
(y-0) = (4-0)/(0-4)×(x-4)
y = -x + 4
So, R{(x,y): 0≤x≤-x+4, 0≤x≤4}
S = √33 \(\int\limits^4_0\int\limits-^x^+^4_0 {} \, dy {} \, dx\)
S = √33\(\int\limits^4_0 {} \,\)(y)dx
S = √33[-x+4-0]₀⁴dx
S = √33(-x²/2 + 4x)₀⁴
S = √33(-4²/2 + 4(4))
S = √33(-8+16)
S = 8√33
Hence, the area of the surface given by z = f(x, y) that lies above the region is 8√33.
To learn more about the area of the surface from the given link
https://brainly.com/question/76387
#SPJ4
find the cost of 24 opera tickets at 112 each
Answers
Answer:
2688
Step-by-step explanation:
Answer:
The answer is - 2688
Step-by-step explanation:
24×112=2688
f(x) = -x^2 + 5x – 2
Find f(-4)
Answers
Answer:
2
Step-by-step explanation:
if f(4), than -4^2=-16
5(4)=20
-16+20-2=2
(+3)- (-3)=
please answer this
please dont delete thhis
Answers
Answer:
6
Step-by-step explanation:
We can rewrite this to 3-(-3). Now, we know if we add a negative value, we will go down some value. Now, if we subtract a negative value, the exact opposite will happen, and instead of going down, you go up, or add that value. We can now rewrite this to 3+3, or 6.
Answer:
6
Step-by-step explanation:
(3)-(-3)
3+3
6
negativexegative is a positive so yup
00:00 Use the numbers shown to complete the table for each value of m. Numbers may be used once, more than once, 26 10 20 2(3m + 7) 6m + 14 2
Answers
we have
2(3m+7)
so
For m=1
substitute
2(3*1+7)
2(1
Please help me with this question!!!!!

Answers
h = 11.9 cm
cos = adjacent/ hypotenuse
therefore:
cos(24) = h/ 13
rearrange:
h = 13cos(24)
put into calculator:
h = 11.8760...
rounded to one decimal point:
h = 11.9cm
What is 5(4x plus 7y) equal to
Answers
Answer:
20x + 35y
Step-by-step explanation:
\(5(4x + 7y) \\ = 5 \times 4x + 5 \times 7y \\ \huge \red{= 20x + 35y}\)
4) Elizabeth waited for 6 minutes at the drive thru at her local McDonald's last time she visited. She was
upset and decided to talk to the manager. The manager assured her that her wait time was very
unusual and that it would not happen again. A study of customers commissioned by this restaurant
found an approximately normal distribution of results. The mean wait time was 226 seconds and the
standard deviation was 38 seconds. Given these data, and using a 95% level of confidence, was
Elizabeth's wait time unusual? Justify your answer.
Answers
Since Elizabeth's z-score of 3.53 is much larger than 1.96, her wait time is significantly further from the mean. This suggests that her wait time is indeed unusual at a 95% level of confidence.
How to solve for the wait timeTo determine if Elizabeth's wait time of 6 minutes (360 seconds) at the drive-thru was unusual, we can compare it to the mean wait time and standard deviation provided.
Given:
Mean wait time (μ) = 226 seconds
Standard deviation (σ) = 38 seconds
Sample wait time (x) = 360 seconds
To assess whether Elizabeth's wait time is unusual, we can calculate the z-score, which measures the number of standard deviations away from the mean her wait time falls:
z = (x - μ) / σ
Plugging in the values, we have:
z = (360 - 226) / 38
z = 134 / 38
z ≈ 3.53
Next, we need to determine if the falls within the range of values considered unusual at a 95% lev z-scoreel of confidence.
For a normal distribution, approximately 95% of the data falls within 1.96 standard deviations of the mean.
Since Elizabeth's z-score of 3.53 is much larger than 1.96, her wait time is significantly further from the mean. This suggests that her wait time is indeed unusual at a 95% level of confidence.
Read more on normal distribution here:https://brainly.com/question/4079902
#SPJ1
Usha had a balance of -$84. She worked for 6 days and put half the money in the bank. Now she had a balanve of -$45. How much does Usha get paid every day for newspaper delivery?
Answers
Answer:
Per day earning is $1.
Step-by-step explanation:
Initial balance that Usha had = $84
Number of working days = 6 days
Total money after working 6 days = $45 × 2 = $90
Since we know that the initial amount is $84 and the final amount is $90. Thus the amount earned by working 6 days is 90 – 84 = $6.
Now we have to calculate the per day earning. Therefore, just divide the earning with number of days.
Per day earning = $6 / 6 = $1
