You need to compute a 90% confidence interval for the population mean. How large a sample should you draw to ensure that the sample mean does not deviate from the population mean by more than 1.4? (Use 7.0 as an estimate of the population standard deviation from prior studies.) Use Table 1. (Round intermediate calculations to 4 decimal places. Round "z-value" to 3 decimal places. Round up your answer to the nearest whole number.)
Answers
As per the given confidence interval, the sample size is 102.
The term confidence interval in math is referred as the mean of your estimate plus and minus the variation in that estimate.
Here we have given that you need to compute a 90% confidence interval for the population mean.
And we need to find the sample size.
While we looking into the given question, we have identified the following values,
Confidence interval = 90% = 0.09
mean = 1.4
Then the sample size is calculated as,
In order to find this one we have to find the critical value of z for 90% confidence level is,
=> z = 1.645
Now, we have to calculate the value of n as,
=> z x σ / √n
when we apply the value on it, then we get,
=> 1.645 x 1.4/√n
When we simplify this one then we get the value of n as 102.
To know more about Confidence interval here.
https://brainly.com/question/24131141
#SPJ4
Related Questions
(a) Show that if λ is an eigenvalue of A, then λ is an eigenvalue of \(A^{T}\). Show with an example that the eigenvectors of A and \(A^{T}\) are not the same.
(b) Show that if λ is an eigenvalue of A, and A is invertible, then λ^-1 is an eigenvalue of A^-1.
Answers
If λ is an eigenvalue of A, then λ is an eigenvalue of \(A^T\). Show with an example that the eigenvectors of A and \(A^T\) are not the same.
What are eigenvalues and eigenvectors?The equation Av = λv, where v is a non-zero vector, is satisfied by an eigenvector v and an eigenvalue given a square matrix A. In other words, the eigenvector v is multiplied by the matrix A to produce a scalar multiple of v. Due to their role in illuminating the behaviour of linear transformations and differential equation systems, eigenvectors play a crucial role in many branches of mathematics and science. When the eigenvector v is multiplied by A, the eigenvalue indicates how much it is scaled.
The eigenvalue and eigenvector states that, let v be a non-zero eigenvector of A corresponding to the eigenvalue λ.
Then, we have:
Av = λv
Taking transpose on both sides we have:
\(v^T A^T = \lambda v^T\)
The above equations thus relates transpose of vector and transpose of A to λ.
Now, consider a matrix:
\(\left[\begin{array}{cc}1&2\\3&4\\\end{array}\right]\)
Now, the eigen values of this matrix are λ1 = -0.37 and λ2 = 5.37.
The eigenvectors are:
\(v1 = [-0.8246, 0.5658]^T\\v2 = [-0.4159, -0.9094]^T\)
Now, for transpose of A:
\(A^T=\left[\begin{array}{cc}1&3\\2&4\\\end{array}\right]\)
The eigen vectors are:
\(u1 = [-0.7071, -0.7071]^T\\u2 = [0.8944, -0.4472]^T\)
Hence, we see that, if λ is an eigenvalue of A, then λ is an eigenvalue of \(A^T\). Show with an example that the eigenvectors of A and \(A^T\) are not the same.
Learn more about eigenvalues here:
https://brainly.com/question/29749542
#SPJ1
Part of the graph of the function f(x) = (x – 1)(x + 7) is shown below.
Which statements about the function are true? Select three options.
The vertex of the function is at (–4,–15).
The vertex of the function is at (–3,–16).
The graph is increasing on the interval x > –3.
The graph is positive only on the intervals where x < –7 and where
x > 1.
The graph is negative on the interval x < –4.
Answers
Answer:
The vertex of the function is at (–3,–16)
The graph is increasing on the interval x > –3
The graph is positive only on the intervals where x < –7 and where
x > 1.
Step-by-step explanation:
The graph of \(f(x)=(x-1)(x+7)\) has clear zeroes at \(x=1\) and \(x=-7\), showing that \(f(x) > 0\) when \(x < -7\) and \(x > 1\). To determine where the vertex is, we can complete the square:
\(f(x)=(x-1)(x+7)\\y=x^2+6x-7\\y+16=x^2+6x-7+16\\y+16=x^2+6x+9\\y+16=(x+3)^2\\y=(x+3)^2-16\)
So, we can see the vertex is (-3,-16), meaning that where \(x > -3\), the function will be increasing on that interval
At a basketball game, a team made 54 successful shots. They were a combination of 1- & 2- point shots. The team scored 90 points in all. Write and solve a system of equations to find the number of each type of shot Equation 1: ______________________ Equation 2: ______________________ 1-point shots: _________ 2-point shots: _________
Answers
Answer:
Your answer is 31 for 1 shot points, and 45 for 2 shot points.
Step-by-step explanation:
The equation y = 65.18x + 21.43 fits the scatterplot of the values for stock
ABC over the past month with an r-value of 0.9874. How much do you think
ABC will be worth at x = 32 days?
Itsjackenley
Answer:
☑️ c. $2107.19

Answers
Answer:
Step-by-step explanation:
Answer:
yeah c?
Step-by-step explanation:
6x^2=-3x+1 to the nearest hundredth
Answers
The solutions to the quadratic equation 6x² = -3x + 1 to the nearest hundredth are -0.73 and 0.23.
What are the solutions to the quadratic equation?Given the quadratic equation in the question:
6x² = -3x + 1
To solve the quadratic equation 6x² = -3x + 1, we can rearrange it into standard form, where one side is set to zero:
6x² + 3x - 1 = 0
Now we can solve the equation using the quadratic formula, which states that for an equation in the form ax² + bx + c = 0, the solutions for x are given by:
\(x = \frac{-b \±\sqrt{b^2-4ac} }{2a}\)
Here; a = 6, b = 3, and c = -1.
Let's substitute these values into the quadratic formula:
\(x = \frac{-b \±\sqrt{b^2-4ac} }{2a}\\\\ x= \frac{-3 \±\sqrt{3^2-4\ *\ 6\ *\ -1} }{2*6}\\\\x = \frac{-3 \±\sqrt{9+24} }{12}\\\\x = \frac{-3 \±\sqrt{33} }{12}\\\\x = -0.73, \ x=0.23\)
Therefore, the values of x are -0.73 and 0.23.
Learn more about quadratic equations here: brainly.com/question/1863222
#SPJ1
what is the property of 3x(5x7)=(3x5)7
Answers
The property you are referring to is called the associative property of multiplication. According to this property, when multiplying three numbers, the grouping of the numbers does not affect the result. In other words, you can change the grouping of the factors without changing the product.
In the equation you provided: 3x(5x7) = (3x5)7
The associative property allows us to group the factors in different ways without changing the result. So, whether we multiply 5 and 7 first, or multiply 3 and 5 first, the final product will be the same.
What is the value of x in the triangle?
3√2
A. 3√2
B. S
C. 6
D. 6√2
E. 2√2
Answers
Answer: D
Step-by-step explanation:
I need to find x and y

Answers
Using the same-side interior angles theorem,
\(8x+30+6x+24=180 \\ \\ 14x+54=180 \\ \\ 14x=126 \\ \\ \boxed{x=9}\)
Using vertical angles,
\(6(9)+24=10y+2 \\ \\ 78=10y+2 \\ \\ 10y=76 \\ \\ \boxed{y=7.6}\)
the formula for the volume of a rectanglular prism is given by
V=lwh
where V is volume, l is length, w is width, and h is height.
a) solve for L if V=120, w=6, and h=4
l=
b) solve for L in general.
l=
Answers
Answer:
Step-by-step explanation:
V=lwh
120=l(6)(4)
120=24I
\(\frac{120}{24} =\frac{24I}{24} \\I=5\)
Answer:
V=lwh
120=l(6)(4)
120=24I\begin{gathered}\frac{120}{24} =\frac{24I}{24} \\I=5\end{gathered}
can someone help me with this question?
Answers
Answer:
what question
Step-by-step explanation:
You are playing a video game. For each diamond you collect, you earn 110 points. You also earn 80 bonus points by completing the level in less than 2 minutes. You need to earn more than 1620 points to continue on to the next level. Write and solve an inequality that represents the numbers d of diamonds you must collect in less than 2 minutes to advance to the next level.
Answers
Answer:
110d + 80 > 1620
d > 14
Step-by-step explanation:
The amount of points from collecting diamonds can be represented by 110d, since you get 110 points for each diamond, d
Add 80 to this to represent the bonus points.
Use a greater than inequality, because you have to get more than 1620 points.
Put this all together:
110d + 80 > 1620
Then, solve for d:
110d + 80 > 1620
110d > 1540
d > 14
So, you have to collect more than 14 diamonds in less than 2 minutes in order to advance to the next level.
PLS HELP 20 PTS
how many solutions are there to this nonlinear system?
a. two solutions
b. no solutions
c. one solution

Answers
Hope this helps
Suppose the price of a sweater is $10. Jaylen's marginal benefit for purchasing each additional sweater is given in the table below. He
gets the most benefit from the first sweater and less benefit from each additional sweater. If Jaylen is behaving rationally, how many
sweaters will he purchase?
1st sweater
2nd sweater
3rd sweater
4th sweater
5th sweater
6th sweater
50
35
30
23
12
8
Answers
The number of sweaters that Jaylen will purchase, based on his marginal benefit, is 5 sweaters.
What is marginal utility?Marginal utility or benefit is the added satisfaction that a consumer derives from the consumption of an additional unit of a product or service.
Using the concept of marginal utility, we can determine the number of units consumers will be willing to purchase.
The law of marginal utility states that a consumer will continue to purchase more of an item until their marginal benefit or utility is fewer than the cost of the item.
For instance, Jaylen will buy sweaters until his marginal benefit is lower than the price of a sweater ($10).
Jaylen is likely to buy 5 sweaters since his marginal benefit, though progressively reducing, still exceeds the price of the sweaters.
Data:Price per sweater = $10
Marginal Benefits
1st sweater 50
2nd sweater 35
3rd sweater 30
4th sweater 23
5th sweater 12
6th sweater 8
Thus, based on marginal utility, Jaylen will purchase 5 sweaters.
Learn more about marginal utility at https://brainly.com/question/15050855
#SPJ1
Which of the following functions is graphed below?
A. y = |x + 5|+ 4
B. y = |x -5| + 4
C. y = |x + 5| - 4
D. y = |x- 5| - 4

Answers
Answer:it’s c y=|x-5|-4
Step-by-step explanation:
The correct function which is graphed is,
D. \(y = |x- 5| - 4\)
We have to give that,
A graph of a function is shown in the image.
Now, From the graph;
Two points on the function are (0, 1) and (5, 4).
Since both points are lies on the graph of a function, hence it satisfies the equation of the function.
From the given function,
A. \(y = |x + 5|+ 4\)
Substitute x = 0, y = 1;
1 = |0 + 5| + 4
1 = 5 + 4
1 = 9
Which is not true.
B. \(y = |x -5| + 4\)
Substitute x = 0, y = 1;
1 = |0 - 5| + 4
1 = 5 + 4
1 = 9
Which is not true.
C. \(y = |x + 5| - 4\)
Substitute x = 0, y = 1;
1 = |0 + 5| - 4
1 = 5 - 4
1 = 1
Which is true.
And, Substitute x = 5, y = 4;
4 = |5 + 5| + 4
4 = 10 + 4
4 = 14
Which is not true.
D. \(y = |x- 5| - 4\)
Substitute x = 0, y = 1;
1 = |0 - 5| - 4
1 = 5 - 4
1 = 1
Which is true.
And, Substitute x = 5, y = 4;
4 = |5 - 5| + 4
4 = 0 + 4
4 = 4
Which is true.
To learn more about the function visit:
https://brainly.com/question/11624077
#SPJ4
PLEASE HELP FAST!! IT IS URGENT!! The owner of a fitness watch would like to determine if the mean number of steps he takes per day differs from the recommended 10,000 steps per day, using a = 0.01. He selects a random sample of 50 days with the intention of testing the hypotheses Hop-10,000 steps versus Hp 10,000 steps where the true mean number of steps taken per day. Which of the following values of the alternative hypothesis would yield the greatest power to reject the null hypothesis?
u=9,000
u=9,500
u = 10,000
u = 10,500
Answers
Answer:
The correct answer is: u = 10,500. When the value of the alternative hypothesis is greater than that of the null hypothesis, the power of the test will be increased, so a value of u = 10,500 would yield the greatest power to reject the null hypothesis.
what is the difference between 42°c and ¬5°c
Answers
Answer:
47° c
Step-by-step explanation:
using the absolute value function to find the difference, that is
difference = | 42 - (- 5) | = | 42 + 5 | = | 47 | = 47
or
difference = | - 5 - 42 | = | - 47 | = 47
PLEASE HELP!! a bag contains 10 marbles. four of them are red, three blue, two white, and one yellow. A mare ke drawn at random. What is the probability that it is blue?

Answers
Answer:
The probability that one marble drawn at random is not blue is 70%
What is the degree of the polynomial, y^2+7x^14-10x^2?
Answers
The degree of the polynomial is 14
How to determine the degree of the polynomial?The polynomial is given as:
y^2+7x^14-10x^2
Here, we assume that the variable of the polynomial is x
The highest power of x in the polynomial y^2+7x^14-10x^2 is 14
Hence, the degree of the polynomial is 14
Read more about polynomial at
https://brainly.com/question/4142886
#SPJ1
what is 4.12 - 2.8 ???
Answers
Answer:
1.32
Step-by-step explanation:
Align the decimal and subtract :)
PLEASE HELP!!! Inequality's

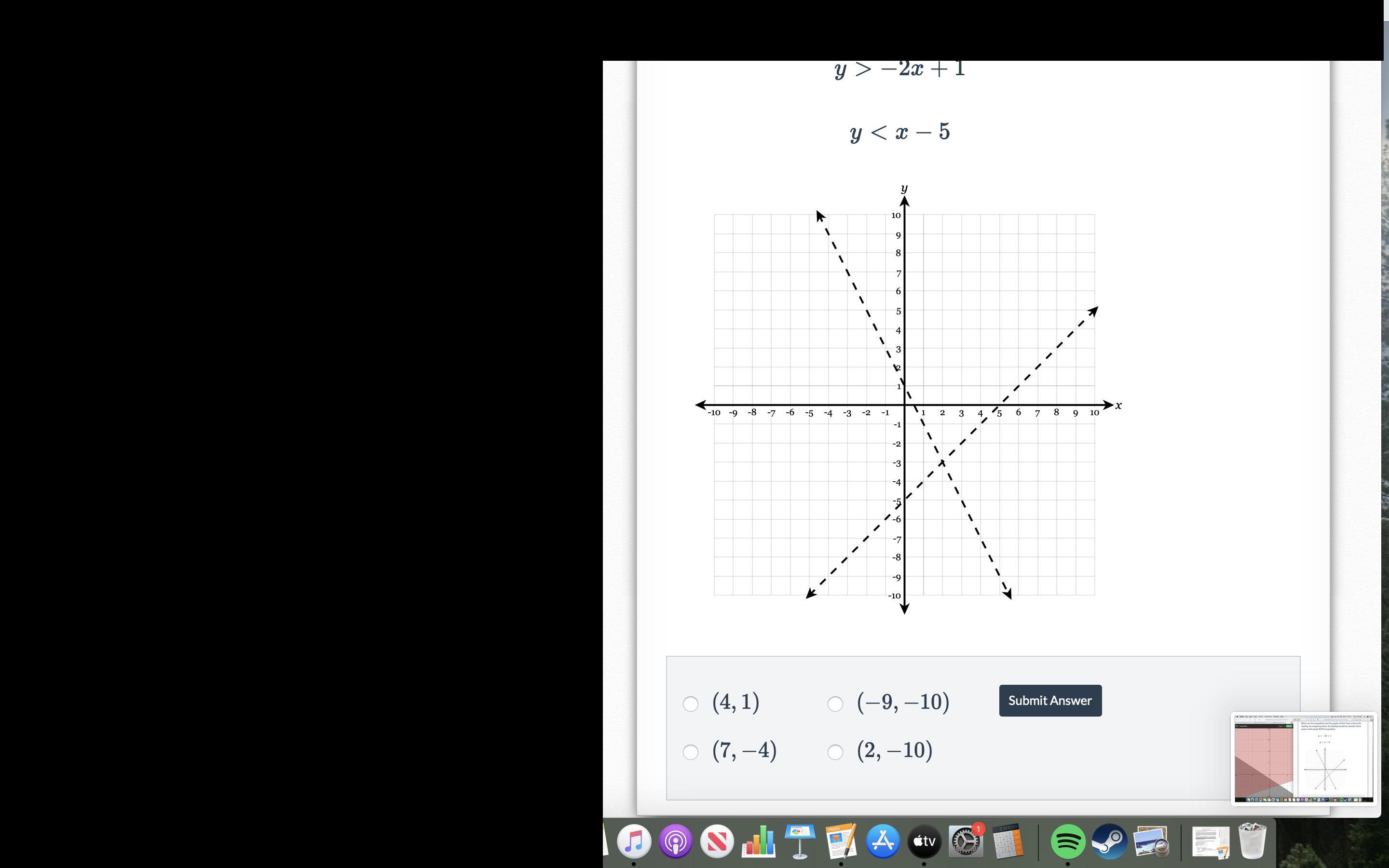
Answers
Answer:
(6,-3) should work but there are infinite answers
Step-by-step explanation:
Find the Laplace transform of the function f(t)=0 , t<1 , t^2-2t+2 , t>1
Answers
The Laplace transform of the given function f(t) is
\(L{f(t)} = (2 / s) - (1 - 2/s) * e^(-s) + (2 / s^2) * e^(-s) + (1 / s)\)
How to find Laplace transformTo find the Laplace transform of the given function f(t),
\(L{f(t)} = \int\limits[0, \infty}) e^(-st) * f(t) * dt\)
where s is the complex Laplace variable.
For t < 1, f(t) = 0
\(L{f(t)} = \int[0, \infty) e^(-st) * 0 * dt = 0\)
For t > 1, f(t) = \(t^2\) - 2t + 2, so the integral becomes:
\(L{f(t)} = \int[1,\infty) e^(-st) * (t^2 - 2t + 2) * dt\)
Now, integrate this expression by parts
\(\int[1,\infty) e^(-st) * (t^2 - 2t + 2) * dt\)
\(= [(-t^2 + 2t - 2) / s * e^(-st)] [1,\infty) + \int[1,\infty) (2t - 2) / s * e^(-st) * dt\)
\(= [(2 / s) * e^(-s)] - [(1 - 2/s) * e^(-s)] + [(-2 / s^2) * e^(-st)] [1,\infty)\)
\(= [(2 / s) - (1 - 2/s) * e^(-s)] + (2 / s^2) * e^(-s)\)
For t = 1, f(t) = 1, add this term to the Laplace transform
\(L{f(t)} = 0 + [(2 / s) - (1 - 2/s) * e^(-s)] + (2 / s^2) * e^(-s) + (1 / s)\)
Hence, the Laplace transform of f(t) is given below
\(L{f(t)} = (2 / s) - (1 - 2/s) * e^(-s) + (2 / s^2) * e^(-s) + (1 / s)\)
Learn more on Laplace transform on https://brainly.com/question/30726222
#SPJ1
the product of 7/8 and 9/10 is greater than 9/10
Answers
Answer:
No
Step-by-step explanation:
7/8x9/10=63/80
So to compare they need to have the same demoninators
9/10x8/8=72/80
The difference of two numbers is 3. Their quotient is 2. What are the two numbers?
Answers
Answer:
The two numbers are 3 and 6.
Step-by-step explanation:
Let one number be a and the other be b.
We're given:
\(a-b=3\)\(\dfrac{a}{b}=2\)Isolate a in the second equation and solve for b:
\(\dfrac{a}{b}=2\\\\a=2b\)
\(a-b=3\\2b-b=3\\b=3\)
Therefore, the second number is 3.
\(a-3=3\\a=6\)
Therefore, the first number is 6.
3. A water pumping station is to be built on a river at point P in order to deliver water to points A and B. The design requires that LAPD = /BPC so that the total length of piping that will be needed is a minimum. Find this minimum length of pipe. B 6.00 mi CH P 12.0 mi A 10.0 mi D
Answers
The minimum length of pipe required to deliver water to points A and B is approximately 20.375 miles.
We are given that a water pumping station is to be built on a river at point P in order to deliver water to points A and B. The design requires that LAPD = /BPC so that the total length of piping that will be needed is a minimum. We need to find this minimum length of pipe.
The given figure is shown below: \(AB = 10 \ miles\)\(BC = 6 \ miles\)\(CP = 12 \ miles\). We are given that \(LAPD = LCPB\).
Now, we need to find the minimum length of pipe required for delivering the water to points A and B.The total length of the pipe, \(L_{total} = LA + AB + BP\)Since \(LAPD = LCPB\), we can say that\(AP^2 + PD^2 = BP^2 + PC^2\).
From the triangle ACP, we can say that\(AC^2 = AP^2 + PC^2\). So, we can substitute AP^2 + PC^2 with AC^2 to get\(AP^2 + PD^2 = BP^2 + AC^2\)Now, we can substitute AP = AC - PC and BP = BC + PC in the above equation to get\((AC - PC)^2 + PD^2 = (BC + PC)^2 + AC^2\).
After solving this equation, we get\(AC = \frac {37}{8}\) and \(PC = \frac {27}{8}\)Now, we can calculate the length of pipe required as follows: \(L_{total} = LA + AB + BP = 10 + 6 + \frac {27}{8} = \boxed{20.375 \ miles}\). Therefore, the minimum length of pipe required to deliver water to points A and B is approximately 20.375 miles.
For more such questions on length, click on:
https://brainly.com/question/2005046
#SPJ8
Based on the supply graph and the demand graph shown above, what is the price at the point of equilibrium?
Hint: Think about the point where they both meet. For example, if you were to place the graphs on top of each other, what would be the point of intersection?
Type the correct number below without the dollar sign.

Answers
Based on the supply graph and demand graph shown above, the price at the point of equilibrium is $ 30.
Demand refers to quantity of a commodity that the consumers are willing to, able to purchase at a given price during a given period of time. Supply refers to quantity of a commodity that the producers are willing to, able to offer for sale at a given price during a given period of time.
Demand curve slopes downward due to inverse relationship between price and quantity demanded whereas supply curve slopes upward due to direct relationship between quantity supplied and price. When both demand and supply curve intersect with each other balance is achieved. Intersection point between demand and supply curve is known as equilibrium.
At this point when prices are equal is known as equilibrium price and when quantiy demanded or supplied are equal it is known as equilibrium quantity. When we combine the given graph. Equilibrium is achieved at a point when price is equal to $ 30 and quantity is equal to 20 units.
To learn more about equilibrium of demand and supply:
https://brainly.com/question/30237240
the 7th grade fundraiser gives away a large container of gumballs to the student who is closest to guessing the correct number of gumballs in the container noticing that the container is a cube. Sally decides to count the number of gumballs along the length of one side if Sally get 729 gumballs how many gumballs did she count along one side of the container
Answers
If the container is a cube, every side is a square, so the length and the width are the same.
To get the number of gumballs based on the number of gumballs in one side, we can use the following equation
\(TotalGumballs=x^3\)Where x is the number of gumballs along one side. So, replacing the total by 729 and solving for x, we get:
\(\begin{gathered} 729=x^3 \\ \sqrt[3]{729}=x \\ 9=x \end{gathered}\)Answer: She counts 9 gumballs along one side of the container
Apples cost $1.99 per pound.
How much do 3.25 pounds of apples cost?
Answers
Answer:
$6.47
Step-by-step explanation:
set up a ratio
\(\frac{1.99}{1} =\frac{x}{3.25}\)
cross multiply
6.47=x
Find the volume of the triangular prism below.
A) 28 cubic feet
B) 168 cubic feet
C) 84 cubic feet
D) 52.5 cubic feet

Answers
Answer:
b.168
Step-by-step explanation:
The side of a triangle are in the ratio 4:4:3 what kind of triangle is it (b) calculate the smallest angle of the triangle to the nearest degree
Answers
The smallest angle of the equilateral triangle is 60 degrees
If the sides of a triangle are in the ratio 4:4:3, it implies that the lengths of the sides are proportional.
To determine the type of triangle, we examine the side lengths. Since all three sides are equal in length, we have an equilateral triangle.
For an equilateral triangle, all angles are equal. To calculate the smallest angle, we divide the total sum of angles in a triangle (180 degrees) by the number of angles, which is 3:
Smallest angle \(= \frac{180}{3} = 60\)\) degrees.
Therefore, the smallest angle of the equilateral triangle is 60 degrees (to the nearest degree).
For more questions on equilateral triangle:
https://brainly.com/question/17264112
#SPJ8
Amy, Justin, and Henry sent a total of 70 text messages during the weekend. Justin sent 10 fewer messages than Amy. Henry sent 2 times as many messages as Amy. How many messages did they each send?
Answers
Answer:
justin 10+ Amy 20 + henry 40+ do answer would be 10+20+50=70
explanation
I took justin and timed it by two then half of 20 is 10 then timed it by two again which 20*2 is 40
add it all together and you get 70
Amy sent 20 messages, Justin 10 messages and Henry 40 messages in total.
System of equationsThese type of equation consists of equation with unknown variables.
Let the number of messages sent by amy be x
Let the number of messages sent by Justin be y
Let the number of messages sent by Henry be z
If the total number od mesages sent is 70, hence;
x + y + z = 70
If Justin sent 10 fewer messages than Amy, then;
y = x - 10
If Henry sent 2 times as many messages as Amy, then;
z= 2x
Substitute
x + x - 10 + 2x = 70
4x = 70 + 10
4x = 80
x = 20
Recall
y = x - 10
y = 10
Also z = 2x
z = 2(20)
z = 40
Hence Amy sent 20 messages, Justin 10 messages and Henry 40 messages in total.
Learn more on system of equation here: https://brainly.com/question/13729904
#SPJ2