You are making snack bags to sell at the fair. You want each bag to contain the same combination of carrot and celery sticks. You have 75 carrot sticks and 40 celery sticks and want to use them all.
What is the greatest number of snack bags you can make
Answers
The greatest number of snack bags is 10.
Highest Common Factor:The largest of all the common factors between two or more numbers is known as the Highest Common Factor (HCF). It is also known as the Greatest Common Element (GCF).
HCF is a fundamental method that allows you to equally distribute items throughout a group or set.
We can use the idea of HCF to determine the same when you are organizing a party and want to make sure that nothing is wasted or you require a proper calculation.
Here we have
Number of carrots = 75
Number of celery sticks = 40
Here we are making snack bags such that each bag contains the same combination of carrot and celery sticks.
To find the greatest number of snack bags we need to find HCF of 70 and 40 as given below
Write given numbers as the product of prime numbers
=> 70 = 2 × 5 × 7
=> 40 = 2 × 2 × 2 × 5
List out the common factors
=> 2 × 5
=> HCF (70, 40) = 10
Therefore,
The greatest number of snack bags is 10.
Learn more about Highest Common Factor at
https://brainly.com/question/802960
#SPJ1
Related Questions
Can you solve this i will give 10 points

Answers
Answer:
2
Step-by-step explanation:
Area = length * width * height
4/5 * 3/2 * 5/3
= 60/30
= 2
Determine the coordinates for the intersection of the diagonals in RSTK with vertices at
R(-8-2).S(-6, 7).
T(67), and U(4-2).
(-1.2.5)
Answers
Answer:
thanks for the points
Step-by-step explanation:
Devaughn is 14 years older than Sydney. The sum of their ages is 110. What is Sydney's age?
Answers
d+s = 76
• substitution;
(s-14)+s = 76
2s-14= 76
2s = 90
s = 45 years old for Sydney
d = s-14 = 31 years old for Devaughn
hope this helps
Answer:
The answer would be 48
Sydney is 48
Devaughn is 62
48 + 62 = 110
Okays so you start by doing the equation 110 - 14 = 96
then dividing 96 by 2 (96 ÷ 2) which is 48
add 14 to 48 and you will get 62. We can automatically assume that sydney is 48 because when you add 48 to 62, you will get 110. I hope that this helps! ^‿^
You model your investment account using the formula y = 20000(1.035)x where x represents the
number of years and y represents the account balance after x years. What is the growth rate of your
investment?
Answers
Answer:
Step-by-step explanation:
The growth rate of the investment is represented by the constant multiplier in the exponential term of the formula y = 20000(1.035)x. In this case, the constant multiplier is 1.035, which represents the annual growth rate of the investment account.
To calculate the growth rate as a percentage, we can subtract 1 from the constant multiplier, and then multiply the result by 100.
So, the growth rate of the investment is:
1.035 - 1 = 0.035
0.035 * 100 = 3.5%
Therefore, the growth rate of the investment is 3.5%.
The growth rate of the investment can be found by subtracting 1 from the base of the exponential function and converting the result to a percentage:
growth rate = (base - 1) x 100%
growth rate = (1.035 - 1) x 100%
growth rate = 0.035 x 100%
growth rate = 3.5%
Therefore, the growth rate of the investment is 3.5%.
PLEASE ANYONE HELP! DONT ANSWER IF UNSURE PLEASE

Answers
Answer:
length 5cm, width 4cm, door width 2/5cm or. 4cm, length 10 ft, width 7.5 ft
elect all equations that represent the number of subscribers, , in terms of months since the beginning of the year (when she had 150 subscribers).
Answers
I need help on this please! Thanks

Answers
Answer:
B. The product of 5 and a number.
Product means multiplication is taking place. In this case, 5 is being multiplied with n.
Hope this helps!
In recent years, Sheffield Transportation purchased three used buses. Because of the frequent turnover in the accounting department, a different accountant was in charge of selecting the depreciation method for each bus, and various methods have been used. Information concerning the buses is summarized in the table below. Bus 1, Bus 2, Bus 3, For the declining-balance method, the company uses the declining method rate. For units-of-activity method, total miles are expected to be 125,000. Actual miles of use in the first 3 years were 2021, 27,000; 2022, 35,000; and 2023, 33,000.
(a1) For Bus #3, calculate depreciation expense per mile under units-of-activity method.
Answers
Under the units-of-activity method, the depreciation expense per mile for Bus #3 is $0.4616.
How is the depreciation expense per mile determined?The units-of-activity method is one of the depreciation methods in use.
Under the units-of-activity method, the depreciation expense per unit is determined by dividing the depreciable amount by the total units of activity.
The depreciation amount (the value of the asset subject to depreciation) is the net of the total cost less the salvage value.
Depreciable amount of Bus #3 = $57,700 ($66,500 - $8,800)
Expected total miles for Bus #3 = 125,000
Depreciation expense per mile for Bus #3 = $0.4616 ($57,700 ÷ 125,000)
Learn more about determining the depreciation expense per unit at https://brainly.com/question/22077069.
#SPJ1
Question Completion:Bus Acquired Cost Salvage Useful Life Depreciation
Value in Years Method
1 1/1/12 $99,100 $7,900 4 Straight-line
2 1/1/12 128,000 11,000 4 Declining- balance
3 1/1/13 66,350 8,800 5 Unit-of-activity
Given vector u=<3,-4> find magnitude and degree
Answers
The sum of magnitude of u + v is 15.99.
What is magnitude?The magnitude or size of a mathematical object is described as a property which determines whether the object is larger or smaller than other objects of the same kind.
Given that, magnitude of u = 5
Magnitude of v = 11
The angle between them i= 40°
we represent u and v in vector form,
u = 5 ( cos 40° i + sin 40° j ) = 3.83 i + 3.21 j
v = 11 ( cos 40° i + sin 40° j ) = 8.42 i + 7.07 j
The sum of two vectors is given by
u + v = 3.83 i + 3.21 j + 8.42 i + 7.07 j
u + v = 12.25 i + 10.28 j
Magnitude of u + v = √(12.25²+10.28²)
Magnitude of u + v
Magnitude of u + v = √( 150.063 + 105.678)
Magnitude of u + v = 15.99
Learn more about vectors form at:
https://brainly.com/question/25705666
#SPJ1
complete question:
Given the magnitudes of vectors u and v and the angle θ between them, find sum of . Give the magnitude to the nearest tenth when necessary and give the direction by specifying the angle that the resultant makes with u to the nearest degree. ∣ u∣ = 5, ∣ v∣ = 11, θ = 40°
how do I understand implicit function
Answers
Answer: An implicit function is a function, written in terms of both dependent and independent variables, like y-3x2+2x+5 = 0. Whereas an explicit function is a function which is represented in terms of an independent variable.
Step-by-step explanation: To find the implicit derivative,
Differentiate both sides of f(x, y) = 0 with respect to x.
Apply usual derivative formulas to differentiate the x terms.
Apply usual derivative formulas to differentiate the y terms along with multiplying the derivative by dy/dx.
Solve the resultant equation for dy/dx (by isolating dy/dx).
How do i solve that question?
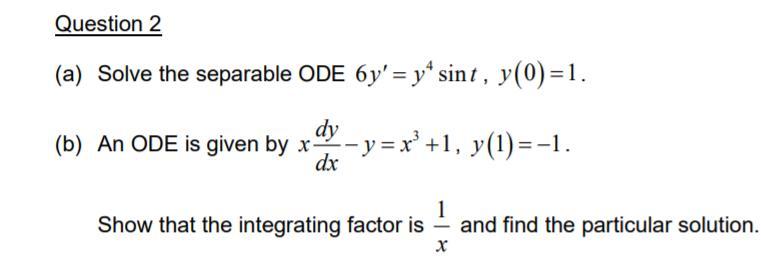
Answers
a) The solution of this ordinary differential equation is \(y =\sqrt[3]{-\frac{2}{\frac{3\cdot t}{8}-\frac{\sin 2t}{4}+\frac{\sin 4t}{32}-2 } }\).
b) The integrating factor for the ordinary differential equation is \(-\frac{1}{x}\).
The particular solution of the ordinary differential equation is \(y = \frac{x^{3}}{2}+x^{2}-\frac{5}{2}\).
How to solve ordinary differential equations
a) In this case we need to separate each variable (\(y, t\)) in each side of the identity:
\(6\cdot \frac{dy}{dt} = y^{4}\cdot \sin^{4} t\) (1)
\(6\int {\frac{dy}{y^{4}} } = \int {\sin^{4}t} \, dt + C\)
Where \(C\) is the integration constant.
By table of integrals we find the solution for each integral:
\(-\frac{2}{y^{3}} = \frac{3\cdot t}{8}-\frac{\sin 2t}{4}+\frac{\sin 4t}{32} + C\)
If we know that \(x = 0\) and \(y = 1\), then the integration constant is \(C = -2\).
The solution of this ordinary differential equation is \(y =\sqrt[3]{-\frac{2}{\frac{3\cdot t}{8}-\frac{\sin 2t}{4}+\frac{\sin 4t}{32}-2 } }\). \(\blacksquare\)
b) In this case we need to solve a first order ordinary differential equation of the following form:
\(\frac{dy}{dx} + p(x) \cdot y = q(x)\) (2)
Where:
\(p(x)\) - Integrating factor\(q(x)\) - Particular functionHence, the ordinary differential equation is equivalent to this form:
\(\frac{dy}{dx} -\frac{1}{x}\cdot y = x^{2}+\frac{1}{x}\) (3)
The integrating factor for the ordinary differential equation is \(-\frac{1}{x}\). \(\blacksquare\)
The solution for (2) is presented below:
\(y = e^{-\int {p(x)} \, dx }\cdot \int {e^{\int {p(x)} \, dx }}\cdot q(x) \, dx + C\) (4)
Where \(C\) is the integration constant.
If we know that \(p(x) = -\frac{1}{x}\) and \(q(x) = x^{2} + \frac{1}{x}\), then the solution of the ordinary differential equation is:
\(y = x \int {x^{-1}\cdot \left(x^{2}+\frac{1}{x} \right)} \, dx + C\)
\(y = x\int {x} \, dx + x\int\, dx + C\)
\(y = \frac{x^{3}}{2}+x^{2}+C\)
If we know that \(x = 1\) and \(y = -1\), then the particular solution is:
\(y = \frac{x^{3}}{2}+x^{2}-\frac{5}{2}\)
The particular solution of the ordinary differential equation is \(y = \frac{x^{3}}{2}+x^{2}-\frac{5}{2}\). \(\blacksquare\)
To learn more on ordinary differential equations, we kindly invite to check this verified question: https://brainly.com/question/25731911
Consider the parabola given by the equation:
f
(
x
)
=
−
2
x
2
−
8
x
+
14
Find the following for this parabola:
A) The value of
f
(
−
5
)
:
B) The vertex = (
,
)
C) The
y
intercept is the point (0,
)
D) Find the two values of
x
that make
f
(
x
)
=
0
. Round your answers to two decimal places. Write the values as a list, separated by commas:
x
=
Answers
Answer:
Sure, here are the answers to your questions:
**A) The value of $f(-5)$ is $-2$.**
To find the value of $f(-5)$, we can simply substitute $x=-5$ into the equation $f(x)=-2x^2-8x+14$. This gives us:
$$f(-5)=-2(-5)^2-8(-5)+14=-2(25)+40+14=-50+54=4$$
**B) The vertex of the parabola is $(2,6)$.**
To find the vertex of the parabola, we can complete the square. This involves adding and subtracting $\left(\dfrac{{b}}{2}\right)^2$ to both sides of the equation, where $b$ is the coefficient of the $x$ term. In this case, $b=-8$, so we have:
$$\begin{aligned}f(x)&=-2x^2-8x+14\\\\ f(x)+20&=-2x^2-8x+14+20\\\\ f(x)+20&=-2(x^2+4x)\\\\ f(x)+20&=-2(x^2+4x+4)\\\\ f(x)+20&=-2(x+2)^2\end{aligned}$$
Now, if we subtract 20 from both sides, we get the equation of the parabola in vertex form:
$$f(x)=-2(x+2)^2-20$$
The vertex of a parabola in vertex form is always the point $(h,k)$, where $h$ is the coefficient of the $x$ term and $k$ is the constant term. In this case, $h=-2$ and $k=-20$, so the vertex of the parabola is $(-2,-20)$. We can also see this by graphing the parabola.
[Image of a parabola with vertex at (-2, -20)]
**C) The $y$-intercept is the point $(0,14)$.**
The $y$-intercept of a parabola is the point where the parabola crosses the $y$-axis. This happens when $x=0$, so we can simply substitute $x=0$ into the equation $f(x)=-2x^2-8x+14$ to find the $y$-intercept:
$$f(0)=-2(0)^2-8(0)+14=14$$
Therefore, the $y$-intercept is the point $(0,14)$.
**D) The two values of $x$ that make $f(x)=0$ are $2.5$ and $-3.5$.**
To find the values of $x$ that make $f(x)=0$, we can set the equation $f(x)=-2x^2-8x+14$ equal to zero and solve for $x$. This gives us:
$$-2x^2-8x+14=0$$
We can factor the left-hand side of the equation as follows:
$$-2(x-2)(x-3)=0$$
This means that either $x-2=0$ or $x-3=0$. Solving for $x$ in each case gives us the following values:
$$x=2\text{ or }x=3$$
However, we need to round our answers to two decimal places. To do this, we can use the calculator. Rounding $x=2$ and $x=3$ to two decimal places gives us the following values:
$$x=2.5\text{ and }x=-3.5$$
Therefore, the two values of $x$ that make $f(x)=0$ are $2.5$ and $-3.5$.
PLZ ANSWER THIS QUESTIONNNN!!!

Answers
Answer:
C
Step-by-step explanation:
180 - 55 = 125
Why 180?
Because 180 is a fixed degree for one straight line
A line passes through the points (-1, 3) and (1, -5). Which points lie on the same line?
Select all that apply.
(0, -2)
(-3, 12)
(-5, 1)
(-2,7)
(4, 15)
(2, -9)
Answers
( 2,-9) points lie on the same line.
Line point intercept is defined.
Quantifying soil cover, including vegetation, litter, rocks, and biotic crusts, quickly and accurately can be done using the line-point intercept approach.
These metrics deal with the erosion caused by wind and water, water infiltration, and the site's capacity to withstand damage and recover from it.
k = -5 - 3/1 - (-1) = -8/2 = -4
the formula of the line is
y - 3 = -4(x+ 1)
when x = -3 , y = 11 ≠ 12 the points aren't on line.
when x = -5, y = 19 ≠ 1
when x = 4, y = -7 ≠ 15
when x = 2, y = -9 ≠ 7
when x = 0, y = -1 ≠ -2
( 2,-9) are on the same line.
Learn more about Line-point intercept
brainly.com/question/1698680
#SPJ9
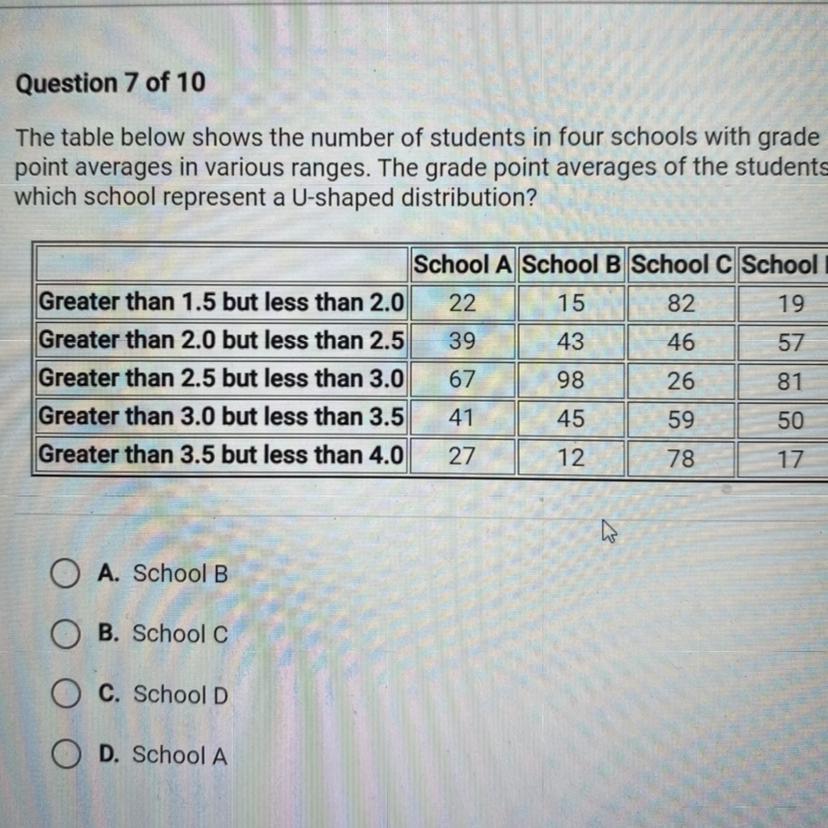
The table below shows the number of students in four schools with grade
point averages in various ranges. The grade point averages of the students in
which school represent a U-shaped distribution?
School A School B School C School D
Greater than 1.5 but less than 2.0 22 15 82 19
Greater than 2.0 but less than 2.5 39 43 46 57
Greater than 2.5 but less than 3.0 67 98 26
81
Greater than 3.0 but less than 3.5 41 45 59 50
Greater than 3.5 but less than 4.0 27 12 78 17
A. School B
O
B. School C
C. School D
Ο Ο
D. School A
Answers
Answer:
b
Step-by-step explanation:
Step-by-step explanation:
school c so B would be correct
The original plan for assigning telephone numbers that you investigated in
Applications Task 4 was implemented in
1947. At that time, the supply of numbers was expected to last for 300 years. However, by the 1970s the numbers were already starting to run out. So, the numbering plan
had to be modified. In this task, you will count the number of different phone numbers that were available in 2012.
a. For three-digit area codes, the first digit cannot be a 0 or a 1. Assuming no additional restrictions, how many three-digit area codes are possible under
this plan?
b. Certain area codes are classified as "Easily Recognizable Codes" (BRCs).
ERCs designate special services, like 888 for toll-free calls. The requirement for an ERC is that the second and third digit of the area code must be the same. The first digit again cannot be a 0 or a 1. How many ERCs are there?
c. Consider the seven digits after the area code. As with the area code, the first digit of the three-digit local prefix cannot be a 0 or a 1. The remaining six digits for the local number have no restrictions. How many of these seven-digit phone numbers are possible?
d. Assuming only the 0 and 1 restrictions in Parts a and c, how many ten-digit phone numbers are possible?
Answers
a. Assuming no additional restrictions, there are 800 possible three-digit area codes.
b. Considering ERCs, there are 80 ERCs.
c. For the seven digits after the area code, there are \(8 \times 10^6 = 8,000,000\) possible seven-digit phone numbers.
d. Assuming only the 0 and 1 restrictions from parts a and c, the number of possible ten-digit phone numbers is 800 \(\times\) 8,000,000 = 6,400,000,000.
a. For three-digit area codes, the first digit cannot be 0 or 1.
Assuming no additional restrictions, there are 8 possibilities for the first digit (2-9) and 10 possibilities for each of the remaining two digits (0-9). Therefore, the total number of three-digit area codes possible under this plan is \(8 \times 10 \times 10 = 800.\)
b. For an ERC (Easily Recognizable Code), the second and third digits of the area code must be the same, and the first digit cannot be 0 or 1. There are 8 possibilities for the first digit (2-9) and 10 possibilities for the third digit (0-9).
Since the second digit must be the same as the third digit, there is only 1 possibility.
Therefore, the total number of ERCs is \(8 \times 1 \times 10 = 80.\)
c. For the seven digits after the area code, the first digit of the three-digit local prefix cannot be 0 or 1.
There are 8 possibilities for the first digit (2-9) and 10 possibilities for each of the remaining six digits (0-9).
Therefore, the total number of seven-digit phone numbers possible is 8 * \(10\times 10 \times 10 \times 10 \times 10 \times 10 = 8,000,000.\)
d. Assuming only the 0 and 1 restrictions from parts a and c, the number of possible ten-digit phone numbers can be calculated by multiplying the number of possibilities for each digit position.
For the area code (part a), there are 800 possibilities.
For the seven digits after the area code (part c), there are 8,000,000 possibilities.
Therefore, the total number of ten-digit phone numbers possible is 800 * 8,000,000 = 6,400,000,000.
For similar question on area codes.
https://brainly.com/question/29279031
#SPJ8
What is the measure of
angle x?
Enter your answer in the box.
X =

Answers
Answer:
x = 48°
Step-by-step explanation:
Complementary angles
Angles that sum to 90°.
Vertical Angle Theorem
When two straight lines intersect, the vertical angles are congruent (equal).
Therefore, angle x is equal to the angle that is complementary to 42°.
To find x, subtract 42° from 90°:
⇒ x = 90° - 42°
⇒ x = 48°

An entrepreneur invests in a new play. The cost includes an overhead of $33,750 plus production costs of $1700 per performance. A sold-out performance brings in $2325 . Assume every performance is sold out, and let x represent the number of sold-out performances.
Answers
The entrepreneur's revenue is $2325x, entrepreneur's cost is $33,750 + $1700x and entrepreneur's profit from x sold-out performances is $625x - $33,750
The entrepreneur's revenue from x sold-out performances is given by the formula:
Revenue = (Price per Performance) x (Number of Performances)
Revenue = $2325 x x
Revenue = $2325x
The entrepreneur's cost from x sold-out performances is given by the formula:
Cost = Overhead + (Production Cost per Performance) x (Number of Performances)
Cost = $33,750 + $1700x
The entrepreneur's profit from x sold-out performances is the revenue minus the cost:
Profit = Revenue - Cost
Profit = $2325x - ($33,750 + $1700x)
Profit = $625x - $33,750
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Please solve this
∫ (log(1 + x ^ 2))/((x + 1) ^ 2) dx
Answers
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
We have,
To solve the integral ∫ (log(1 + x²) / (x + 1)²) dx, we can use the method of substitution.
Let's substitute u = x + 1, which implies du = dx. Making this substitution, the integral becomes:
∫ (log(1 + (u-1)²) / u²) du.
Expanding the numerator, we have:
∫ (log(1 + u² - 2u + 1) / u²) du
= ∫ (log(u² - 2u + 2) / u²) du.
Now, let's split the logarithm using the properties of logarithms:
∫ (log(u² - 2u + 2) - log(u²)) / u² du
= ∫ (log(u² - 2u + 2) / u²) du - ∫ (log(u²) / u²) du.
We can simplify the second integral:
∫ (log(u²) / u²) du = ∫ (2 log(u) / u²) du.
Using the power rule for integration, we can integrate both terms:
∫ (log(u² - 2u + 2) / u²) du = log(u² - 2u + 2) / u - 2 ∫ (log(u) / u³) du.
Now, let's focus on the second integral:
∫ (log(u) / u³) du.
This integral does not have a simple closed-form solution in terms of elementary functions.
It can be expressed in terms of a special function called the logarithmic integral, denoted as Li(x).
Therefore,
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
Learn more about integrations here:
https://brainly.com/question/30217024
#SPJ1
Determine the equation of the circle with center (0, -2) containing the point
(√12,-5).
Answers
Answer:
i think its
x^2 + (y + 2)^2 = 21.
Step-by-step explanation:
Which has the least value for 9? *
A. 1.95
B. 0.1039
C. 3.092
D. 2.009
Answers
Answer:
0.1039
Step-by-step explanation:
Obtain the place value of 9 in each value and choose the smallest :
1.95
9 is the first digit after the decimal point ; which is equal to 0.9 = tenth place
0.1039
9 is the 4th digit after the decimal point ; which is equal to 0.0009 = ten thousandth place
3.092
9 is the second digit after the decimal point ; which is equal to 0.09 = hundredth place
2.009
9 is the third digit after the decimal point ; which is equal to 0.009 = thousandth place
Hence the smallest value of 9 among the options given resides in 0.1039 (ten thousandth place).
The graph of the function f(x) = (x - 3)(x + 1) is shown.

Answers
Answer:
the second one
Step-by-step explanation:
y is postitive when x < -1 and x > 3, but y is decreasing only when x < 1 so the case where both are true is when x < -1 option 2
i need help on this thank you

Answers
PLEAS ANSWER ASAP I WILL GIVE BRIAINLYIST
The coordinates of the vertices of a polygon are (-3, 1), (-3, 3), (-1, 5), (2, 4), and (2, 1).
What is the perimeter of the polygon to the nearest tenth of a unit?
A. 16.0 units
B. 17.2 units
C. 15.4 units
D. 18.8 units
Answers
Using the coordinates of the vertices of a polygon (-3, 1), (-3, 3), (-1, 5), (2, 4), and (2, 1) the perimeter of the polygon is 16.0 units
How to find the perimeter of the polygonThe perimeter is calculated by summing the sides
The length of line in an ordered pair is calculated using the formula
d = √{(x₂ - x₁)² + (y₂ - y₁)²}
where
d = distance between the points
x₂ and x₁ = points in x coordinates
y₂ and y₁ = points in y coordinates
(-3, 1) and (-3, 3) =√{(-3 - -3)² + (3 - 1)²} = 2
(-3, 3) and (-1, 5) = √{(-1 - -3)² + (5 - 3)²} = 2√2
(-1, 5) and (2, 4) = √{(2 - -1)² + (4 - 5)²} = √10
(2, 4) and (2, 1) = √{(2 - 2)² + (1 - 4)²} = 3
(2, 1) and (-3, 1) = √{(-3 - 2)² + (1 - 1)²} = 5
The perimeter = 2 + 2√2 + √10 + 3 + 5
The perimeter = 15.9907
The perimeter = 16.0 units
Learn more about length of line segment here:
https://brainly.com/question/24778489
#SPJ1
which relation by a graph is a function?
i cannot fit the 3rd graph in the pic brw

Answers
Neither of the graphs in the picture is a function
To be a function it needs to pass the vertical line test, which both of them fail.
NO LINKS!! Please help me with this problem. Find all points on the x-axis that are a distance 5 from P(-8,4)

Answers
Answer:
\((x,y)=\left(\; \boxed{-11,0}\; \right)\; \textsf{(smaller $x$-value)}\)
\((x,y)=\left(\; \boxed{-5,0}\; \right)\; \textsf{(larger $x$-value)}\)
Step-by-step explanation:
\(\boxed{\begin{minipage}{4 cm}\underline{Equation of a circle}\\\\$(x-a)^2+(y-b)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(a, b)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)
The points that are a distance of 5 units from P(-8, 4) will be all the points on the circumference of a circle with center (-8, 4) and radius 5.
Substitute the center and radius into the formula to create an equation of the circle:
\(\implies (x+8)^2+(y-4)^2=25\)
The y-value of any point on the x-axis is zero.
Therefore, to find the points on the x-axis that are 5 units from point P, substitute y = 0 into the equation of the circle and solve for x:
\(\implies (x+8)^2+(0-4)^2=25\)
\(\implies (x+8)^2+(-4)^2=25\)
\(\implies (x+8)^2+16=25\)
\(\implies (x+8)^2+16-16=25-16\)
\(\implies (x+8)^2=9\)
\(\implies \sqrt{(x+8)^2}=\sqrt{9}\)
\(\implies x+8=\pm3\)
\(\implies x+8-8=\pm3-8\)
\(\implies x=-8\pm3\)
\(\implies x=-11, x=-5\)
Therefore:
\((x,y)=\left(\; \boxed{-11,0}\; \right)\; \textsf{(smaller $x$-value)}\)
\((x,y)=\left(\; \boxed{-5,0}\; \right)\; \textsf{(larger $x$-value)}\)

what does x=?........................

Answers
Answer:
x = -25 / 3
Step-by-step explanation:
10 / 3 = x / (-5/2)
10 / 3 * (-5 / 2) = x
x = -50 / 6
x = -25 / 3
Answer:
\(x=\frac{-25}{3}\)
Step-by-step explanation:
\(\frac{10}{3}=\frac{x}{\frac{-5}{2} } \\\\\frac{-5}{2}*\frac{10}{3}=\frac{x}{\frac{-5}{2} }*\frac{-5}{2} \\\\\frac{-25}{3} =x\\\\x=\frac{-25}{3}\)
In a diagram, ∠A and ∠B are vertical angles, and ∠B is a complementary angle with ∠C. If ∠A=22°, write an equation that you can use to solve for ∠C.
Answers
Answer:
22° + m<C = 90°
Step-by-step explanation:
Pre-SolvingWe are given that <A (which is equal to 22°) and <B are vertical angles, and that <B is complementary to <C.
We want to write an equation that will help us solve <C.
SolvingRecall that vertical angles are congruent by vertical angles theorem.
This means that <A ≅ <B; it also means that the measure of <B is also 22°.
Also recall that complementary angles add up to 90°.
This means that m<B + m<C = 90°.
Since we deduced that m<B is 22°, we can substitute that value into the equation.
Hence, an equation that can be used to solve for <C is:
22° + m<C = 90°
Name the characteristics a shape has to have to be defined as the following
quadriatera
Triangle
square
Answers
Answer:
A quadrilateral is a shape that has four straight sides and four angles.
A triangle is a shape that has three straight sides and three angles.
A square is a special type of quadrilateral that has four straight sides of equal length and four right angles.
PLEASE I NEED HELP!!! FIRST ANSWER IS BRANLIEST!!!
Apply the distributive property to create an equivalent expression. 6(5x-3)
Answers
Answer:
30x - 18
Step-by-step explanation:
6(5x - 3)
Apply the distributive property.
6(5x) + 6(-3)
30x + - 18
Answer:
30x - 18 is your final answer