write an iterated integral for over the region r described to the right using a) vertical cross-sections, b) horizontal cross-sections.
Answers
Since the problem does not specify the region r, we cannot provide a specific iterated integral. However, we can provide the general formulas for writing an iterated integral over a region using vertical or horizontal cross-sections.
a) For vertical cross-sections, we integrate with respect to x first, and then integrate with respect to y over the range of y values that correspond to each vertical strip of the region. The formula is:
∫∫ f(x,y) dA = ∫ [y_min(x), y_max(x)] ∫ f(x,y) dy dx
where y_min(x) and y_max(x) are the lower and upper bounds for y that correspond to the region bounded by the vertical line x.
b) For horizontal cross-sections, we integrate with respect to y first, and then integrate with respect to x over the range of x values that correspond to each horizontal strip of the region. The formula is:
∫∫ f(x,y) dA = ∫ [x_min(y), x_max(y)] ∫ f(x,y) dx dy
where x_min(y) and x_max(y) are the lower and upper bounds for x that correspond to the region bounded by the horizontal line y.
To know more about iterated integral refer here:
https://brainly.com/question/29632155
#SPJ11
Related Questions
an island is 1 mi due north of its closest point along a straight shoreline. a visitor is staying at a cabin on the shore that is 15 mi west of that point. the visitor is planning to go from the cabin to the island. suppose the visitor runs at a rate of 6 mph and swims at a rate of 2.5 mph. how far should the visitor run before swimming to minimize the time it takes to reach the island? round your answer to three decimal places and omit units from the answer box.
Answers
if the visitor runs at a rate of 6 mph and swims at a rate of 2.5 mph., then the visitor would run 14 .45 miles before swimming to minimize the time it takes to reach the island .
we are given that an island is 1 mi due north of its closest point along a straight shoreline., where the visitor is staying at a cabin on the shore that is 15 mi west of that point, in some point the visitor runs at a rate of 6 mph and swims at a rate of 2.5 mph. Considering x be the distance the visitor runs. so the total time will be :
Time (T)= x/6 + √((15-x)²+1²)/2.5
Differntiating both sides respect to x , we get
dT/dx = 1/6 -(15-x)/√(15-x)²+1)/2.5
=>1/6 = (15-x)/√(15-x)²+1)/2.5
=>6(15-x) = 2.5√(15-x)²+1)
Now considering 15 - x = y, we get
=>6y = 2.5√(y²+1)
=>36y² = 6.25y² + 6.25
=>29.75y² = 6.25
y = √(25/119), therefore ,x = 15 - √(25/119) = 14 .45
to know more about the rate refer to the link https://brainly.com/question/19593764?referrer=searchResults.
#SPJ4
Which of the following is not a function?

Answers
Answer:
The first option.... The one with the blue dot I guess you have chosen that
Mark has only used 8.5% of a 34-oz bottle of shampoo. How many ounces has he used?
Answers
Given:
Mark has only used 8.5% of a 34-oz bottle of shampoo.
To find:
How many ounces has he used?
Solution:
According to the question,
Shampoo used by Mark = 8.5% of a 34-oz
\(=\dfrac{8.5}{100}\times 34\text{-oz}\)
\(=0.085\times 34\text{-oz}\)
\(=2.89\text{-oz}\)
Therefore, he used 2.89-oz of shampoo.
Find the common ratio for this geometric sequence.0.7, 2.1, 6.3, 18.9,...A. 1.4B. 3C-3O D. 0.33
Answers
We will ahve the following:
\(\frac{2.1}{0.7}=3\)\(\frac{6.3}{2.1}=3\)\(\frac{18.9}{6.3}=3\)So, the common ratio for the geometric sequence is 3. [Option B]
(
3.9
×
10
−
5
)
(
7
×
10
−
3
)
Answers
Answer:
2278
Step-by-step explanation:
(3.9×10−5)(7×10−3)
= (39 - 5)(7 x 10 -3)
= (39 - 5)(70-3)
= 34(70-3)
= 34 x 67
= 2278
The mean number of pets per household is 2.96 with standard deviation 1.4. A sample of 52 households is drawn. Find the 74th percentile of the sample mean.
Answers
The 74th percentile of the sample mean for the number of pets per household is approximately 3.08.
To find the 74th percentile of the sample mean when the mean number of pets per household is 2.96 with a standard deviation of 1.4 and a sample size of 52 households, you can follow these steps:
1. Determine the standard error of the sample mean.
The standard error (SE) is calculated by dividing the population standard deviation by the square root of the sample size:
SE = σ / √n
SE = 1.4 / √52
SE ≈ 0.194
2. Determine the z-score associated with the 74th percentile.
You can use a z-table or a calculator to find the z-score that corresponds to a cumulative probability of 0.74. The z-score is approximately 0.63.
3. Calculate the sample mean associated with the 74th percentile by using the z-score, the population mean, and the standard error:
Sample mean = μ + z * SE
Sample mean = 2.96 + 0.63 * 0.194
Sample mean ≈ 3.08
Learn more about percentile:
https://brainly.com/question/28839672
#SPJ11
If Y has a binomial distribution with parameters n and p, then p(hat)1 = Y/n is an unbiased estimator of p. Another estimator of p is p(hat)2 = (Y+1)/(n+2).
a. Derive the biase of p(hat)2.
b. Derive MSE(Pphat)1) and MSE(p(hat)2).
c. For what values of p is MSE(p(hat)1) < MSE(p(hat)2)?
Answers
a. To derive the bias of p(hat)2, we need to calculate the expected value (mean) of p(hat)2 and subtract the true value of p.
Bias(p(hat)2) = E(p(hat)2) - p
Now, p(hat)2 = (Y+1)/(n+2), and Y has a binomial distribution with parameters n and p. Therefore, the expected value of Y is E(Y) = np.
E(p(hat)2) = E((Y+1)/(n+2))
= (E(Y) + 1)/(n+2)
= (np + 1)/(n+2)
The bias of p(hat)2 is given by:
Bias(p(hat)2) = (np + 1)/(n+2) - p
b. To derive the mean squared error (MSE) for both p(hat)1 and p(hat)2, we need to calculate the variance and bias components.
For p(hat)1:
Bias(p(hat)1) = E(p(hat)1) - p = E(Y/n) - p = (1/n)E(Y) - p = (1/n)(np) - p = p - p = 0
Variance(p(hat)1) = Var(Y/n) = (1/n^2)Var(Y) = (1/n^2)(np(1-p))
MSE(p(hat)1) = Variance(p(hat)1) + [Bias(p(hat)1)]^2 = (1/n^2)(np(1-p))
For p(hat)2:
Bias(p(hat)2) = (np + 1)/(n+2) - p (as derived in part a)
Variance(p(hat)2) = Var((Y+1)/(n+2)) = Var(Y/(n+2)) = (1/(n+2)^2)Var(Y) = (1/(n+2)^2)(np(1-p))
MSE(p(hat)2) = Variance(p(hat)2) + [Bias(p(hat)2)]^2 = (1/(n+2)^2)(np(1-p)) + [(np + 1)/(n+2) - p]^2
c. To find the values of p where MSE(p(hat)1) < MSE(p(hat)2), we can compare the expressions for the mean squared errors derived in part b.
(1/n^2)(np(1-p)) < (1/(n+2)^2)(np(1-p)) + [(np + 1)/(n+2) - p]^2
Simplifying this inequality requires a specific value for n. Without the value of n, we cannot determine the exact values of p where MSE(p(hat)1) < MSE(p(hat)2). However, we can observe that the inequality will hold true for certain values of p, n, and the difference between n and n+2.
To learn more about binomial distribution: -brainly.com/question/29137961
#SPJ11
In the given scenario, we have two estimators for the parameter p of a binomial distribution: p(hat)1 = Y/n and p(hat)2 = (Y+1)/(n+2). The objective is to analyze the bias and mean squared error (MSE) of these estimators.
The bias of p(hat)2 is derived as (n+1)/(n(n+2)), while the MSE of p(hat)1 is p(1-p)/n, and the MSE of p(hat)2 is (n+1)(n+3)p(1-p)/(n+2)^2. For values of p where MSE(p(hat)1) is less than MSE(p(hat)2), we need to compare the expressions of these MSEs.
(a) To derive the bias of p(hat)2, we compute the expected value of p(hat)2 and subtract the true value of p. Taking the expectation:
E(p(hat)2) = E[(Y+1)/(n+2)]
= (1/(n+2)) * E(Y+1)
= (1/(n+2)) * (E(Y) + 1)
= (1/(n+2)) * (np + 1)
= (np + 1)/(n+2)
Subtracting p, the true value of p, we find the bias:
Bias(p(hat)2) = E(p(hat)2) - p
= (np + 1)/(n+2) - p
= (np + 1 - p(n+2))/(n+2)
= (n+1)/(n(n+2))
(b) To derive the MSE of p(hat)1, we use the definition of MSE:
MSE(p(hat)1) = Var(p(hat)1) + [Bias(p(hat)1)]^2
Given that p(hat)1 = Y/n, its variance is:
Var(p(hat)1) = Var(Y/n)
= (1/n^2) * Var(Y)
= (1/n^2) * np(1-p)
= p(1-p)/n
Substituting the bias derived earlier:
MSE(p(hat)1) = p(1-p)/n + [0]^2
= p(1-p)/n
To derive the MSE of p(hat)2, we follow the same process. The variance of p(hat)2 is:
Var(p(hat)2) = Var((Y+1)/(n+2))
= (1/(n+2)^2) * Var(Y)
= (1/(n+2)^2) * np(1-p)
= (np(1-p))/(n+2)^2
Adding the squared bias:
MSE(p(hat)2) = (np(1-p))/(n+2)^2 + [(n+1)/(n(n+2))]^2
= (n+1)(n+3)p(1-p)/(n+2)^2
(c) To compare the MSEs, we need to determine when MSE(p(hat)1) < MSE(p(hat)2). Comparing the expressions:
p(1-p)/n < (n+1)(n+3)p(1-p)/(n+2)^2
Simplifying:
(n+2)^2 < n(n+1)(n+3)
Expanding:
n^2 + 4n + 4 < n^3 + 4n^2 + 3n^2
To learn more about binomial distribution: -brainly.com/question/29137961
#SPJ11
Determine the actual area of logo 1 in square ft

Answers
The actual area of the logo 1 is 24ft²
What is area of shape?The area of a shape is the space occupied by the boundary of a plane figures like circles, rectangles, and triangles.
The actual sides of the logo 1 will be;
base = 1/2 in
= 1/2 × 8 = 4ft
small base = 1/4 × 8 = 2ft
The logo can be sub divided into two equal trapezoid.
area of trapezoid = 1/2 (a+b)h
= 1/2( 4+8) 2
= 12 ft²
area of the logo = 2 × 12 = 24ft²
Therefore the area of the logo is 24ft²
learn more about area of shape from
https://brainly.com/question/25965491
#SPJ1
Matt starts swimming lessons on 5 day . He goes every 10 days . How many lessons will Matt go to in 30 days?
Answers
Answer: 3 lessons
Step-by-step explanation:
Matt starts swimming lessons on Day 5.
He then goes to swimming lessons every 10 days. The dates he went on lessons are therefore:
First lesson = Day 5
Second lesson = Day 5 + 10 days = Day 15
Third lesson = Day 15 + 10 days = Day 25
Fourth lesson = Day 25 + 10 days= Day 35
He therefore only went for 3 lessons because the 4th lesson was after Day 30.
FIND X AND Y
HELP PLZ ASAP
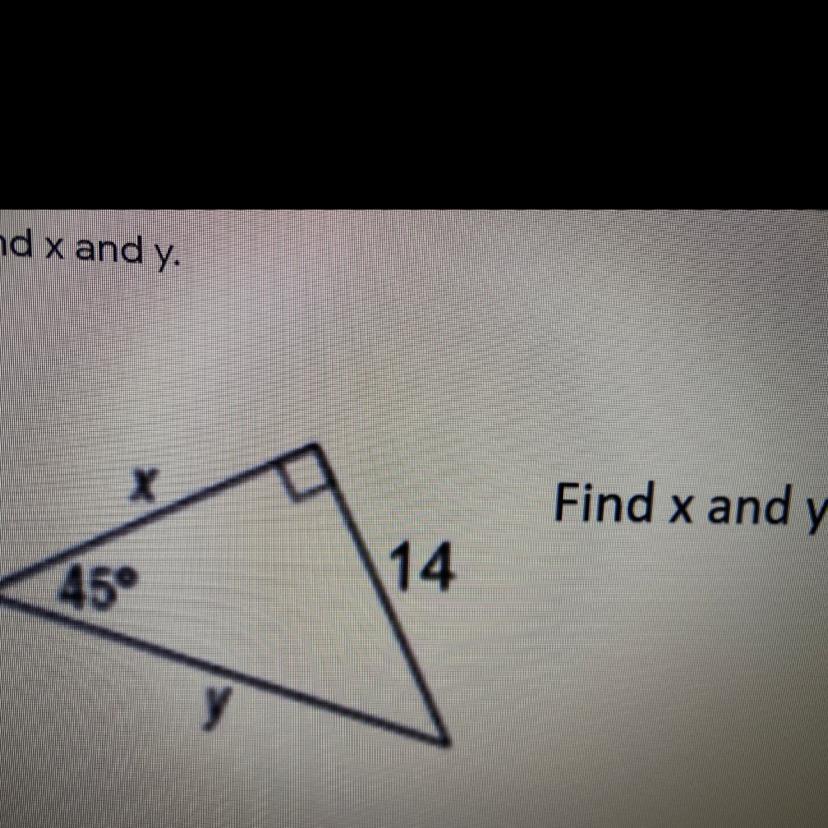
Answers
Answer:
x equals 14, y equals 19.8
Step-by-step explanation:
g Lovely Lawns, Inc., intends to use sales of lawn fertilizer to predict lawn mower sales. The store manager estimates a probable six-week lag between fertilizer sales and mower sales. The pertinent data are: PeriodFertilizer SalesNumber of Mowers Sold 11.915 21.612 31.713 41.915 52.116 61.813 71.914 81.713 91.815 101.412 111.814 121.714 131.714 141.612 a. Determine the correlation between the two variables.
Answers
The correlation between variables (r) = 0.959, and signifies a positive relationship between the variables.
What is correlation?The correlation of two pairs of data values tells about the degree of movement(along or opposite) that can occur in one of the data values when other data value is increased or decreased respectively.
The pertinent data are:
Period Fertilizer Sales Number of Mowers Sold
1 1.6 12.0
2 1.3 10.0
3 1.8 13.0
4 2.0 15.0
5 2.2 15.0
6 1.5 11.0
7 1.6 12.0
8 1.4 10.0
9 1.8 13.0
10 1.4 10.0
11 1.9 15.0
12 1.4 11.0
13 1.7 14.0
14 1.4 13.0
To determine the correlation between the two variables
Regression equation ( y ) = a + bx
y = dependent variable ( mower )
x = independent variable ( fertilizer)
a = intercept point ( y-axis and regression line )
b = slope ( regression line )
From the given data;
N = 14 , Σ x = 22.8,
Σy = 131, Σy^2 = 1269,
Σx^2 = 38.18, (Σx)^2 = 519.84
Σxy = 219.8, (Σy)^2 = 17161
Hence, The correlation between variables (r) = 0.959, and signifies a positive relationship between the variables.
Learn more about coefficient of a determination here:
https://brainly.com/question/13699432
#SPJ1
PLEASE HELP!! its due in 20 minutes and i dont get this

Answers
Answer:
Please see below :)
Step-by-step explanation:
The slope is just what's in front of the x!
So:
1.) slope = -1/4
2.) slope = undefined
3.) slope = -9
4.) slope = 9/2
Hope this helps!
Answer:
1. -1/4
2. undefined
3. zero
4. 6/5
Step-by-step explanation:
Julio has $150. Each week, he saves an additional $10.Write a function ()that models the total amount of money Julio has after weeks.
Answers
Answer:
The function that models the total amount of money Julio has after weeks is:
f(x)=150+10x, where:
x is the number of weeks
Step-by-step explanation:
With the information provided, you can say that the total amount of money Julio has would be equal to the initial amount he has plus the result of multiplying the $10 that he saves every week for the number of weeks, which can be expressed as:
f(x)=150+10x, where:
x is the number of weeks
Answer: f(x)=150+10x,
Step-by-step explanation:
What is Regression in math.
Answers
Answer:
Regression is a statistical technique or method that evaluates the relationship between one dependent variable (usually denoted by Y) and a set of other variables (known as independent variables or regressors)
Step-by-step explanation:

what kinds of numbers are exact? check all that apply. what kinds of numbers are exact?check all that apply.
Answers
Option A: defined quantities, option C: integers that are part of a mathematical equation, and option D: measurements that can be counted, are all kinds of numbers that are exact.
A value that is known with 100 percent confidence is called an exact number. In other terms, an exact integer has an infinite number of significant digits and zero uncertainty. It is impossible to simplify or reduce an exact number. Defined quantities like volume in liters, integers that are a part pf mathematical equation like 4π\(r^{3}\), and countable measurements such as the number of students is exact number that can be quantified.
Determining if a particular unit is an exact number can be challenging because not all units and their conversions have clear definitions. Since the SI base units have all been specified, they are all precise integers. Imperial units that are defined in accordance with the SI base units are likewise precise numbers.
To know more about exact numbers, refer:
https://brainly.com/question/27219805
#SPJ4
Complete question is:
What kinds of numbers are exact?
Check all that apply.
A) Defined quantities (e.g., 1000 mL in 1 liter).
B) The readings of the thermometer.
C) Integers that are part of a mathematical equation (e.g., 4πr33)
D) Measurements that can be counted, such as the number of students in class.
Can someone help me with this, please?
No links or false answers, please

Answers
Refer to the attachments!!~
\(\rule{300pt}{3pt}\)




The exact value is found by making use of order of operations. The
functions can be resolved using the characteristics of quadratic functions.
Correct responses:
\(\displaystyle 1\frac{4}{7} \div \frac{2}{3} - 1\frac{5}{7} =\frac{9}{14}\)x = -4, y = 12When P = 1, V = 6\(\displaystyle x = -3 \ or \ x = \frac{1}{2}\)\(\displaystyle i. \hspace{0.1 cm} \underline{ f(x) = 2 \cdot \left(x - 1.25 \right)^2 + 4.875 }\)
ii. The function has a minimum point
iii. The value of x at the minimum point, is 1.25
iv. The equation of the axis of symmetry is x = 1.25
Methods by which the above responses are foundFirst part:
The given expression, \(\displaystyle \mathbf{ 1\frac{4}{7} \div \frac{2}{3} -1\frac{5}{7}}\), can be simplified using the algorithm for arithmetic operations as follows;
\(\displaystyle 1\frac{4}{7} \div \frac{2}{3} - 1\frac{5}{7} = \frac{11}{7} \div \frac{2}{3} - \frac{12}{7} = \frac{11}{7} \times \frac{3}{2} - \frac{12}{7} = \frac{33 - 24}{14} =\underline{\frac{9}{14}}\)Second part:
y = 8 - x
2·x² + x·y = -16
Therefore;
2·x² + x·(8 - x) = -16
2·x² + 8·x - x² + 16 = 0
x² + 8·x + 16 = 0
(x + 4)·(x + 4) = 0
x = -4y = 8 - (-4) = 12
y = 12Third part:
(i) P varies inversely as the square of V
Therefore;
\(\displaystyle P \propto \mathbf{\frac{1}{V^2}}\)
\(\displaystyle P = \frac{K}{V^2}\)
V = 3, when P = 4
Therefore;
\(\displaystyle 4 = \frac{K}{3^2}\)
K = 3² × 4 = 36
\(\displaystyle V = \sqrt{\frac{K}{P}\)
When P = 1, we have;
\(\displaystyle V =\sqrt{ \frac{36}{1} } = 6\)
When P = 1, V = 6Fourth Part:
Required:
Solving for x in the equation; 2·x² + 5·x - 3 = 0
Solution:
The equation can be simplified by rewriting the equation as follows;
2·x² + 5·x - 3 = 2·x² + 6·x - x - 3 = 0
2·x·(x + 3) - (x + 3) = 0
(x + 3)·(2·x - 1) = 0
\(\displaystyle \underline{x = -3 \ or\ x = \frac{1}{2}}\)Fifth part:
The given function is; f(x) = 2·x² - 5·x + 8
i. Required; To write the function in the form a·(x + b)² + c
The vertex form of a quadratic equation is f(x) = a·(x - h)² + k, which is similar to the required form
Where;
(h, k) = The coordinate of the vertex
Therefore, the coordinates of the vertex of the quadratic equation is (b, c)
The x-coordinate of the vertex of a quadratic equation f(x) = a·x² + b·x + c, is given as follows;
\(\displaystyle h = \mathbf{ \frac{-b}{2 \cdot a}}\)
Therefore, for the given equation, we have;
\(\displaystyle h = \frac{-(-5)}{2 \times 2} = \mathbf{ \frac{5}{4}} = 1.25\)
Therefore, at the vertex, we have;
\(k = \displaystyle f\left(1.25\right) = 2 \times \left(1.25\right)^2 - 5 \times 1.25 + 8 = \frac{39}{8} = 4.875\)
a = The leading coefficient = 2
b = -h
c = k
Which gives;
\(\displaystyle f(x) \ in \ the \ form \ a \cdot (x + b)^2 + c \ is \ f(x) = 2 \cdot \left(x + \left(-1.25 \right) \right)^2 +4.875\)
Therefore;
\(\displaystyle \underline{ f(x) = 2 \cdot \left(x -1.25\right)^2 + 4.875}\)ii. The coefficient of the quadratic function is 2 which is positive, therefore;
The function has a minimum point.iii. The value of x for which the minimum value occurs is -b = h which is therefore;
The x-coordinate of the vertex = h = -b = 1.25
iv. The axis of symmetry is the vertical line that passes through the vertex.
Therefore;
The axis of symmetry is the line x = 1.25.Learn more about quadratic functions here:
https://brainly.com/question/11631534
write the quadratic equation in standard form x squared + 3x = 8
Answers
Answer:
\(x^{2}\) + 3x - 8 = 0
Step-by-step explanation:
ax² + bx + c = 0 (standard form)
Answer:
x² + 3x = 8
Step-by-step explanation:
list all the elements of each set. (Note that sometimes you will have to put three dots at the end because the set is infinite.) E={All possible remainders from dividing a natural number by 6}.
PLEASE HELP I GIVE BRAINLIEST :D
Answers
\(E=\{0,1,2,3,4,5\}\)
The remainders from dividing a natural number by a natural number \(n\) are \(0,1,2,3,\ldots,n-1\).
Evaluate the indefinite integral. Use a capital " C " for any constant term. ∫(3ex+4x5−x34+1)dx= TIP Enter your answer as an expression. Example: 3x∧2+1,x/5,(a+b)/c Be sure your variables match those in the question
Answers
The equatiion where C is the constant of integration.To evaluate the indefinite integral ∫(3e^x + 4x^5 - x^3/4 + 1)dx, we can integrate each term separately.
∫3e^x dx = 3∫e^x dx = 3e^x + C₁
∫4x^5 dx = 4∫x^5 dx = 4 * (1/6)x^6 + C₂ = (2/3)x^6 + C₂
∫-x^3/4 dx = (-1/4)∫x^3 dx = (-1/4) * (1/4)x^4 + C₃ = (-1/16)x^4 + C₃
∫1 dx = x + C₄
Now, we can combine these results to obtain the final answer:
∫(3e^x + 4x^5 - x^3/4 + 1)dx = 3e^x + (2/3)x^6 - (1/16)x^4 + x + C
Therefore, the indefinite integral of (3e^x + 4x^5 - x^3/4 + 1)dx is:
∫(3e^x + 4x^5 - x^3/4 + 1)dx = 3e^x + (2/3)x^6 - (1/16)x^4 + x + C
where C is the constant of integration.
Learn more about integration here:brainly.com/question/32510822
#SPJ11
the volume of a tree stump can be modeled by considering it as a right cylinder. evelyn measures its circumference as 197 in and its volume as 92650 cubic inches. find the height of the stump in feet. round your answer to the nearest tenth if necessary.
Answers
The height of the tree stump is 2.48 feet.
To find the height of the tree stump, we can use the formula for the volume of a right cylinder: \(V = \pi r^2h\), where V represents the volume, r represents the radius, and h represents the height.
Given that the circumference of the tree stump is measured as 197 inches, we can use the formula for the circumference of a circle: C = 2πr, where C represents the circumference.
From the given circumference, we can solve for the radius, r, by dividing the circumference by 2π: r = C / (2π).
Plugging in the given circumference of 197 inches, we have: r = 197 / (2π) ≈ 31.416 inches.
Now, we can substitute the known values of the volume and radius into the volume formula: 92650 = π(31.416)^2h.
To solve for the height, h, we divide both sides of the equation by π(31.416)^2: h = 92650 / (π(31.416)^2) ≈ 29.74 inches.
Since we want to convert the height from inches to feet, we divide the height by 12: h = 29.74 / 12 ≈ 2.48 feet.
Therefore, the height of the tree stump is approximately 2.48 feet.
For more question on height visit:
https://brainly.com/question/28990670
#SPJ8
It is assumed that approximately 15% of adults in the U.S. are left-handed. Consider the probability that among 100 adults selected in the U.S., there are at least 30 who are left-handed. Given that the adults surveyed were selected without replacement, can the probability be found by using the binomial probability formula with x counting the number who are left-handed? Who or why not?
Answers
No, we cannot use the binomial probability formula with x counting the number who are left-handed in this case
This is because the adults surveyed were selected without replacement. The binomial distribution requires that the samples are independent and identically distributed (i.e., the probability of success remains constant for each trial).
However, when we sample without replacement, the probabilities are not constant because the population size changes with each selection. This means that the probability of selecting a left-handed person for the first selection is not the same as the probability of selecting a left-handed person for the second selection, and so on. Therefore, we cannot use the binomial distribution to calculate the probability of at least 30 left-handed adults among 100 selected without replacement from the US population.
Instead, we can use the hypergeometric distribution to calculate the probability of at least 30 left-handed adults among 100 selected without replacement from the US population. The hypergeometric distribution takes into account the changing probabilities as each selection is made without assuming that the selections are independent.
For more such questions on binomial probability
https://brainly.com/question/9325204
#SPJ4
Everyone at your school has to take one art class, so 115 students take glass blowing, 90 students take cave painting, and 15 students take both. The wisest 120 students take photography for an easy A. How many total students are at your school?
Answers
115 + 90 + 15 + 120 = 340
So
AUB=A+B-(A$\cap$ B)AUB=115+90-15AUB=100+90AUB=190Total students
190+120310Bryan divided 3/4 of a liter of plant fertilizer evenly among some smaller bottles. He put 3/8 of a liter into each bottle. How many smaller bottles did Bryan fill?
Answers
Therefore, Bryan filled 2 smaller bottles.
Bryan divided 3/4 of a liter of plant fertilizer evenly among some smaller bottles.
He put 3/8 of a liter into each bottle. We need to find how many smaller bottles Bryan filled.
To find the number of smaller bottles filled by Bryan, we need to divide the total amount of fertilizer by the amount in each bottle.
Dividing 3/4 by 3/8 is equivalent to multiplying 3/4 by 8/3:(3/4) × (8/3) = 24/12 = 2
Since 3/4 of a liter was divided evenly among some smaller bottles, and each bottle received 3/8 of a liter, Bryan filled 2 smaller bottles (24/12 = 2).
To know more about fertilizer visit
https://brainly.com/question/14012927
#SPJ11
9.70 suppose that y1, y2,..., yn constitute a random sample from a poisson distribution with mean λ. find the method-of-moments estimator of λ.
Answers
The method-of-moments estimator for λ is simply the sample mean, which is, λ_hat = (1/n) * ∑yi, where i = 1 to n, where λ_hat is the estimator of λ, yi are the observed values of the random sample, and n is the sample size.
The Poisson distribution is used to model the probability of a certain number of events occurring in a fixed interval of time or space when these events occur independently and at a constant rate.
In the method-of-moments, we equate the sample moments to their corresponding population moments and solve for the unknown parameter. For the Poisson distribution, the mean and variance are both equal to λ.
Thus, the method-of-moments estimator for λ is simply the sample mean, which is:
λ_hat = (1/n) * ∑yi, where i = 1 to n
Where λ_hat is the estimator of λ, yi are the observed values of the random sample, and n is the sample size.
To know more about Poisson distribution, here
brainly.com/question/17157139
#SPJ4
Find the derivative, but do not simplify your answer.
y = (5x6 − 3x4 + 2x2 − 1)(4x9 + 3x7 − 5x2 + 4x)
y'= ?
Answers
The derivative of y = (5x6 − 3x4 + 2x2 − 1)(4x9 + 3x7 − 5x2 + 4x) is (30x^5 - 12x^3 + 4x)(4x^9 + 3x^7 - 5x^2 + 4x) + (5x^6 - 3x^4 + 2x^2 - 1)(36x^8 + 21x^6 - 10x + 4).
Using the product rule of differentiation, we have:
y' = (5x^6 - 3x^4 + 2x^2 - 1)'(4x^9 + 3x^7 - 5x^2 + 4x) + (5x^6 - 3x^4 + 2x^2 - 1)(4x^9 + 3x^7 - 5x^2 + 4x)'
Taking the derivative of the first term using the power rule, we get:
(5x^6 - 3x^4 + 2x^2 - 1)' = 30x^5 - 12x^3 + 4x
Taking the derivative of the second term using the product rule, we get:
(4x^9 + 3x^7 - 5x^2 + 4x)' = 36x^8 + 21x^6 - 10x + 4
Therefore, we have:
y' = (30x^5 - 12x^3 + 4x)(4x^9 + 3x^7 - 5x^2 + 4x) + (5x^6 - 3x^4 + 2x^2 - 1)(36x^8 + 21x^6 - 10x + 4)
To learn more about derivative here:
https://brainly.com/question/25324584
#SPJ4
3. Reports B05 and B06 contain a lot of information. What seems to be the purpose of this information? (You will need some practice to use these reports. )
Answers
Without specific information about the content of reports B05 and B06, it is difficult to determine their exact purpose.
However, based on the given statement that the reports contain a lot of information and may require practice to use effectively, we can make some general assumptions about their purpose.
1. Information analysis and decision-making: Reports B05 and B06 likely provide detailed data and analysis on a particular subject or topic. They may present information in a structured and organized manner, allowing users to make informed decisions based on the fractions data provided.
2. Performance evaluation and improvement: The reports may contain performance metrics, statistics, or feedback on a specific process, project, or system. The purpose could be to assess performance, identify areas for improvement, and track progress over time.
3. Research and exploration: Reports B05 and B06 may serve as a resource for research purposes, providing comprehensive information and analysis on a specific subject. Researchers or analysts may refer to these reports to gain insights or support their own studies.
4. Communication and documentation: The reports may act as a means of communication and documentation, conveying information to stakeholders, clients, or team members. They could summarize findings, highlight key points, and serve as a reference for future discussions or actions.
It's important to note that the actual purpose of reports B05 and B06 can vary depending on the specific context, industry, or organization involved.
learn more about fractions here: brainly.com/question/10354322
#SPJ11
Which sentences represent the inequality? check all that apply. 2.1 (-1.2x) greater-than-or-equal-to 8 the sum of 2.1 and –1.2 times a number is at least 8. the sum of 2.1 and –1.2 times a number is no more than 8. the sum of 2.1 and –1.2 times a number is a maximum of 8. the sum of 2.1 and –1.2 times a number is greater than or equal to 8. the sum of 2.1 and –1.2 times a number is a minimum of 8.
Answers
The best interpretation is that the sum of 2.1 and –1.2 times a number is greater than or equal to 8.
Inequality functionsInequality are expressions not separated by an equal sign, Given the inequality;
2.1 + (-1.2x) ≥ 8
The sign ≥ means greater than or equal to
The expression 2.1 + (-1.2x) ≥ 8 can also be expressed as 2.1 - 1.2x ≥ 8
The best interpretation is that the sum of 2.1 and –1.2 times a number is greater than or equal to 8.
Learn more on inequality here: https://brainly.com/question/11613554
#SPJ4
Answer:
The 1st, 4th, and 5th
Step-by-step explanation:
Ulse the standard normal distribution or the f-distribution to construct a 95% confidence interval for the population meare Justify your decion, il newter distribution can bo used, explain why. Interpret the results In a randorn sample of 46 people, the mean body mass index (BMI) was 27.2 and the standard devation was 6.0f. Which distribution should be used to construct the confidence interval? Choose the correct answer below. A. Use a 1-distribuition because the sample is random, the population is normal, and σ is uricnown 8. Use a normal distribution because the sample is random, the population is normal, and o is known. C. Use a nomal distribution because the sample is random, n≥30, and α is known. D. Use a t-distribution because the sample is random, n≥30, and σ is unknown. E. Neither a normal distribution nor a t-distribution can be used because either the sample is not random, of n < 30 , and the population a nat known to be normal.
Answers
We can be 95% confident that the true population mean BMI is between 25.368 and 29.032.
A 95% confidence interval for the population mean can be constructed using the t-distribution when the sample size is small (<30) or the population standard deviation is unknown.
In this case, we have a random sample of 46 people with a mean body mass index (BMI) of 27.2 and a standard deviation of 6.0.
Thus, we need to use the t-distribution to construct the confidence interval.
The formula for the confidence interval is as follows:
Upper limit of the confidence interval:27.2 + (2.013) (6.0/√46) = 29.032Lower limit of the confidence interval:27.2 - (2.013) (6.0/√46) = 25.368
Therefore, the 95% confidence interval for the population mean BMI is (25.368, 29.032).
This means that we can be 95% confident that the true population mean BMI is between 25.368 and 29.032.
To learn more about true population visit:
https://brainly.com/question/32979836
#SPJ11
assuming this data is accurate and stable, what is the probability that a randomly selected christian living in the united states would identify as catholic?
Answers
The probability that a randomly selected Christian living in the United States would identify as Catholic can be calculated by dividing the number of Catholics in the US by the total number of Christians in the US.
To do this calculation, we need to know the accurate data on the number of Catholics and the total number of Christians in the US. Let's assume that there are X Catholics and Y total Christians in the US.
The probability of a randomly selected Christian being Catholic would be:
P(Catholic) = X/Y
Without the accurate data on the number of Catholics and total Christians in the US, it is not possible to calculate the exact probability. However, if we assume that the data provided is accurate and stable, we can use the formula above to calculate the probability.
Learn more about probability
brainly.com/question/30034780
#SPJ11
Triangle QRS has been rotated 90° to create triangle TVU. Using the image below, prove that lines RS and VU have the opposite and reciprocal slopes.

Answers
Answer:
If the line RS has been rotated 90 degrees, then VU will be perpendicular to RS and the two slopes must be opposite and reciprocal, i.e. product of the two slopes will equal -1.
As a verification, we find the locations of V and U from rotations of R & S.
(actually, the triangle had been rotated -90°, 90 ° clockwise)
Step-by-step explanation:
Slope RS, m1:
Slope VU, m2
Hence m1*m2=1*-1=-1, meaning that m1 and m2 are opposite (in sign) and are reciprocal to each other, as expected
The lines RS and VU have the opposite and reciprocal slopes because Slope of QRS is 1, where as Slope of TVU is -1
What is slope of a triangle?
Slope of a triangle represents the angle that are formed between positve X-axis moving anticlockwise towards y-axis.
The slope of triangle QRS,RQ=3
SQ=3
slope (Tan∅)=\(\frac{perpendicular}{base}\)
=RQ/SQ
=3/3 =1
TanФ=45°
The slope of triangle TUV,UT=3
VT=-3
slope (Tan∅)=\(\frac{perpendicular}{base}\)
=UT/VT
=3/-3 =-1
TanФ=135°
Slope of QRS is 1, where as
Slope of TVU is -1
∴ RS and VU have the opposite and reciprocal slopes.
Learn more about slope here: https://brainly.com/question/3493733
#SPJ2