which statement about the graph of the line y=x+1/2 will be true if the 1/2 is replaced by -2
Answers
Answer:
Step-by-step explanation:
it help me alot
Related Questions
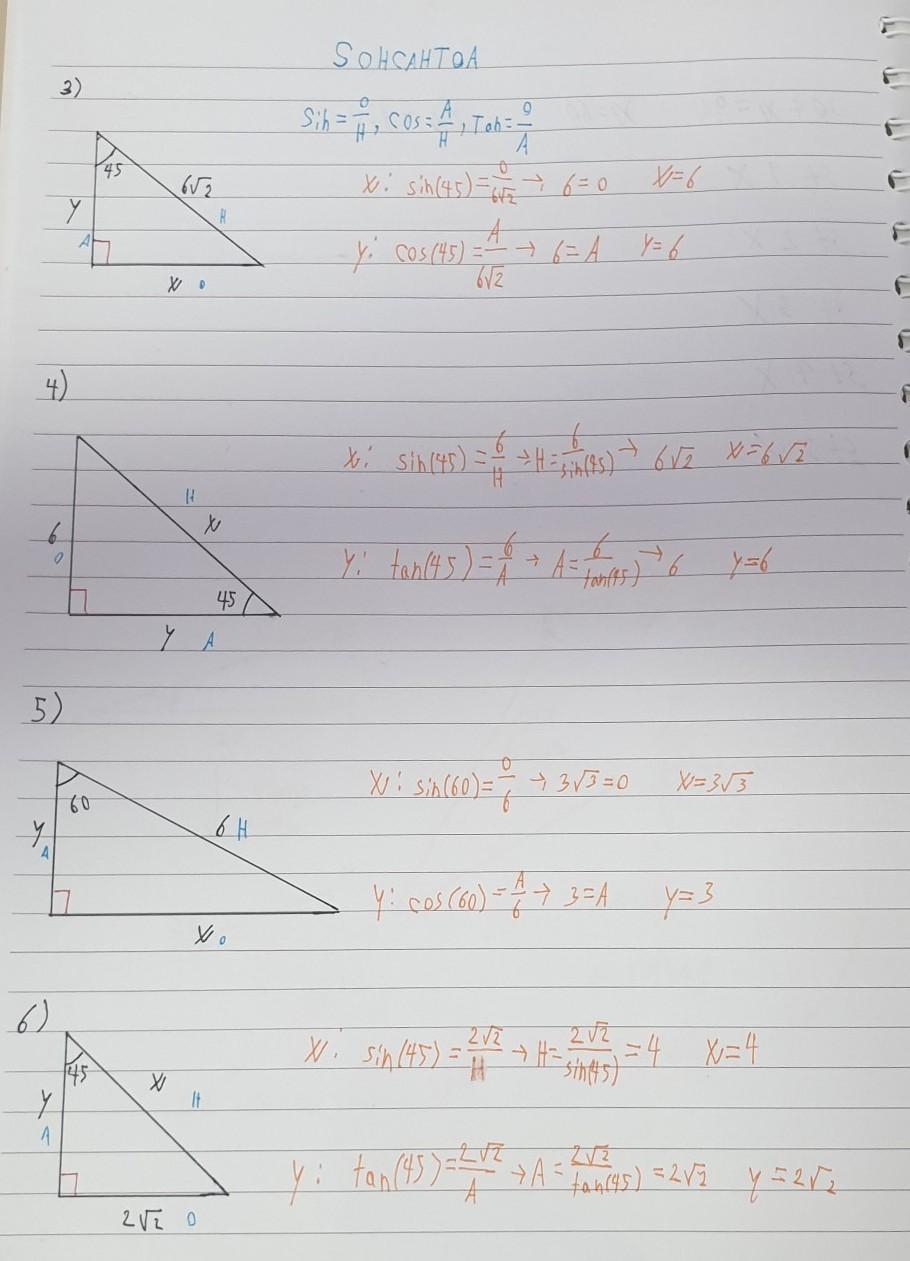
help me find the missing sides to solve this equation

Answers
Step-by-step explanation:
use the function sohcahtoa to solve as all these triangles are right angled
Let G be a finite group and p a prime. A theorem of Cauchy says that if p divides the order of G, then G contains an element of order p. Prove this in two parts. (a) Prove it when G is abelian. (b) Use the class equation to prove it when G is nonabelian.
Answers
Let G be a finite group and p a prime. A theorem of Cauchy says that if p divides the order of G, then G contains an element of order p. Prove this in two parts. (a) Prove it when G is abelian. (b) Use the class equation to prove it when G is nonabelian.Proof of Cauchy's Theorem Let G be a finite group and p be a prime number such that p divides the order of G. Let's assume that G is abelian first.
So, we want to show that G contains an element of order p. We will proceed by induction on the order of G. If the order of G is 1, then G contains only the identity element. It is of order p, which means that the statement is true. If the order of G is greater than 1, then we can pick an element g in G which is not the identity element. We will consider two cases: Case 1: The order of g is divisible by p. In this case, we are done since g is an element of order p. Case 2: The order of g is not divisible by p.
In this case, we consider the group H generated by g. Since H is a subgroup of G, the order of H divides the order of G. Also, the order of H is greater than 1 since it contains g. Therefore, p divides the order of H. By induction, there exists an element h in H such that the order of h is p. Since h is in H, it can be written as a power of g. Hence, g^(m*p) = h^m = e, where e is the identity element of G. This means that the order of g is at most p. But we know that the order of g is not divisible by p. Therefore, the order of g is p itself. So, G contains an element of order p if G is abelian.
To know more about Cauchy's Theoremb visit:
https://brainly.com/question/31058232
#SPJ11
A clinical trial is conducted to compare an experimental medication to placebo to reduce the symptoms of asthma. Two hundred participants are enrolled in the study and randomized to receive either the experimental medication or placebo. The primary outcome is a self-reported reduction of symptoms. Among 100 participants who received the experimental medication, 38 reported a reduction of symptoms as compared to 21 participants of 100 assigned to the placebo.
a. Generate a 95% confidence interval (CI) for the difference in proportions of participants reporting a reduction of symptoms between the experimental and placebo groups.
b. Estimate the relative risk (RR) for reduction in symptoms between groups.
c. Estimate the odds ratio (OR) for reduction in symptoms between groups.
d. Generate a 95% confidence interval (CI) for the relative risk (RR).
Answers
The true relative risk of the experimental medication lies between 1.17 and 3.53 with 95% certainty.
Generate a 95% confidence interval (CI) for the difference in proportions of participants reporting a reduction of symptoms between the experimental and placebo groups. The formula for the 95% confidence interval (CI) for the difference in proportions of participants reporting a reduction of symptoms between the experimental and placebo groups is given by; CI = (p1 - p2) ± 1.96 * √ [(p1 * (1 - p1) / n1) + (p2 * (1 - p2) / n2)
Where;
p1 = the proportion of participants in the experimental group that reported a reduction of symptoms
p2 = the proportion of participants in the placebo group that reported a reduction of symptoms
n1 = the number of participants in the experimental group
n2 = the number of participants in the placebo group
Substitute the values into the formula.
p1 = 38/100 = 0.38
p2 = 21/100 = 0.21
n1 = n2 = 100
CI = (0.38 - 0.21) ± 1.96 * √ [(0.38 * (1 - 0.38) / 100) + (0.21 * (1 - 0.21) / 100)]
CI = 0.17 ± 1.96 * 0.079
CI = 0.17 ± 0.155
CI = (0.015, 0.325). Hence, the 95% confidence interval (CI) for the difference in proportions of participants reporting a reduction of symptoms between the experimental and placebo groups is (0.015, 0.325).
Estimate the relative risk (RR) for reduction in symptoms between groups.
The formula for calculating the relative risk (RR) is given by;
RR = (a / (a + b)) / (c / (c + d))
Where;
a = number of participants who received the experimental medication and reported a reduction in symptoms
b = number of participants who received the experimental medication but did not report a reduction in symptoms
c = number of participants who received the placebo and reported a reduction in symptoms
d = number of participants who received the placebo but did not report a reduction in symptoms
Substitute the values into the formula.
a = 38
b = 62
c = 21
d = 79
RR = (38 / (38 + 62)) / (21 / (21 + 79))
RR = 0.38 / 0.21
RR = 1.81
Hence, the relative risk (RR) for reduction in symptoms between the experimental and placebo groups is 1.81.
Estimate the odds ratio (OR) for reduction in symptoms between groups.
The formula for calculating the odds ratio (OR) is given by;
OR = (a * d) / (b * c)
Substitute the values into the formula.
a = 38
b = 62
c = 21
d = 79
OR = (38 * 79) / (62 * 21)
OR = 1.44
Hence, the odds ratio (OR) for a reduction in symptoms between the experimental and placebo groups is 1.44. Generate a 95% confidence interval (CI) for the relative risk (RR).
The formula for calculating the standard error (SE) of the logarithm of the relative risk is given by;
SE = √ [(1 / a) - (1 / (a + b)) + (1 / c) - (1 / (c + d))]
The formula for calculating the confidence interval (CI) of the relative risk is given by; CI = e^(ln(RR) - 1.96 * SE) to e^(ln(RR) + 1.96 * SE)
Substitute the values into the formulas
SE = √ [(1 / 38) - (1 / (38 + 62)) + (1 / 21) - (1 / (21 + 79))]
SE = 0.283
CI = e^(ln(1.81) - 1.96 * 0.283) to e^(ln(1.81) + 1.96 * 0.283)
CI = 1.17 to 3.53
Hence, the 95% confidence interval (CI) for the relative risk (RR) is (1.17 to 3.53). The clinical trial was conducted to compare the effectiveness of an experimental medication to placebo in reducing the symptoms of asthma. The trial consisted of 200 participants who were randomly assigned to receive either the experimental medication or placebo. The primary outcome of the trial was a self-reported reduction of symptoms. Of the 100 participants who received the experimental medication, 38 reported a reduction in symptoms as compared to 21 participants who received the placebo. The results of the study were analyzed to generate a 95% confidence interval (CI) for the difference in proportions of participants reporting a reduction of symptoms between the experimental and placebo groups. The 95% CI was found to be (0.015, 0.325), which means that the true difference in proportions of participants reporting a reduction of symptoms between the experimental and placebo groups lies between 0.015 and 0.325 with 95% certainty. Hence, the experimental medication is statistically significant in reducing the symptoms of asthma compared to placebo. The relative risk (RR) was estimated to be 1.81, which indicates that the experimental medication is 1.81 times more effective in reducing the symptoms of asthma compared to placebo.
The odds ratio (OR) was estimated to be 1.44, which indicates that the odds of experiencing a reduction in symptoms in the experimental group were 1.44 times higher than the odds in the placebo group. A 95% CI for the relative risk (RR) was also generated, which was found to be (1.17 to 3.53). This means that the true relative risk of the experimental medication lies between 1.17 and 3.53 with 95% certainty. The clinical trial showed that the experimental medication is more effective in reducing the symptoms of asthma compared to the placebo.
To know more about asthma visit:
brainly.com/question/29626405
#SPJ11
Determine whether each triangle with sides of given lengths is a right triangle. 2 m, 5 m, 6 m
Answers
The triangle with the lengths 2m, 5m and 6m is not a right triangle, as the lengths do not form a Pythagorean triple.
What is the Pythagorean Theorem?The Pythagorean Theorem states that for a right triangle, the length of the hypotenuse squared is equals to the sum of the squared lengths of the sides of the triangle.
The sum of the two smaller sides squared is given as follows:
2² + 5² = 4 + 25 = 29.
The square of the largest side is of:
6² = 36.
As 29 is different of 36, the Pythagorean Theorem is not respected, and thus the triangle is not a right triangle.
More can be learned about the Pythagorean Theorem at brainly.com/question/30203256
#SPJ1
determine a region whose area is equal to the given limit. do not evaluate the limit.
Answers
The obtained limit is identical to the limit that was specified. Therefore, the right answer is option C.
What is a region whose area is equal to the given limit?Generally, the equation for the limit is mathematically given as
\($\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \frac{4}{n} \sqrt{1+\frac{4 i}{n}}$.\)
The goal is to locate the zone whose area corresponds to the value supplied by the limit.
The definite integral of a function is what is used to compute the area of that function that is underneath its graph.
The limit,
\(\lim _{n \rightarrow \infty} \sum_{i=1}^{n} f(a+i \cdot \Delta x) \Delta x\)
where\($\Delta x=\frac{b-a}{n}$\) and \($x_{i}=a+i \Delta x$\) for the interval $[a, b]$, is equivalent to the integral
\(\int_{a}^{b} f(x) d x .\)
The given limit can also be written as
\(\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \sqrt{1+\left(\frac{4}{n}\right)} i \cdot \frac{4}{n} .\)
In this limit, \($\Delta x=\frac{4}{n}$\). It can be observed that\($f(a+i \Delta x)=\sqrt{1+\left(\frac{4}{n}\right)} i$\) which implies that \($a=1$ and $f(x)=\sqrt{x}$.\)
Solve the \($\Delta x=\frac{b-a}{n}$\)equation for as follows:
\(\begin{aligned}\frac{4}{n} &=\frac{b-1}{n} \\4 &=b-1 \\5 &=b\end{aligned}\)
Therefore, the specified limit may be expressed as an integral as follows:
\(\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \sqrt{1+\left(\frac{4}{n}\right) i} \cdot \frac{4}{n}=\int_{1}^{5} \sqrt{x} d x\)
Therefore, the limit that has been provided designates the area of the graph of "sqrt(x)" on the interval.[1,5]
However, none of the available choices are compatible with this choice. So, consider
\(a=0, f(x)=\sqrt{1+x}$ and $\Delta x=\frac{4}{n}$.\)
Find the value of $b$ as:
\($$\begin{aligned}\frac{4}{n} &=\frac{b-0}{n} \\4 &=b\end{aligned}$$\)
Find the value of x_{i} as:
\(\begin{aligned}&x_{i}=0+\frac{4}{n} i \\&x_{i}=\frac{4}{n} i\end{aligned}\)
$$
Thus, the integral \($\int_{0}^{4} \sqrt{1+x} d x$\) can be expressed using the equation \($\int_{a}^{b} f(x) d x=\lim _{n \rightarrow \infty} \sum_{i=1}^{n} f\left(x_{i}\right) \Delta x$\)
\(\begin{aligned}\int_{0}^{4} \sqrt{1+x} d x &=\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \sqrt{1+\frac{4 i}{n} \frac{4}{n}} \\&=\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \frac{4}{n} \sqrt{1+\frac{4 i}{n}}\end{aligned}\)
In conclusion, The obtained limit is identical to the limit that was specified. Therefore, the right answer is option C.
Read more about region
https://brainly.com/question/13162113
#SPJ4
CQ
The complete Question is attached below

−7+11p=3p−47
what is p?
Answers
Answer:
p= -5
Step-by-step explanation:
because UwU and also −7+11p=3p−47
−7+11p=3p+−47
11p−7=3p−47
11p−7−3p=3p−47−3p
8p−7=−47 8p−7+7=−47+7
8p=−40 8p /8 = −40 /8
Answer:
P= -5
Step-by-step explanation:
Does there exist an 8 x 8 matrix A = (a) satisfying the following three conditions? (i) If i j then a = 0 (ii) a18 #0 (a18 denotes the entry in the first row and eighth column of A) (iii) A is diagonalizable If such a matrix exists, provide an example of one and prove that it satisfies the given three conditions. If no such matrix exists, prove that no such matrix exists
Answers
We need to determine whether an 8x8 matrix A exists that satisfies three conditions:
(i) having zeros below the main diagonal,
(ii) having a non-zero entry in the first row and eighth column, denoted as a18
(iii) being diagonalizable. In the second paragraph.
we will either provide an example of such a matrix and prove that it satisfies the conditions, or prove that no such matrix exists.
To provide an example of an 8x8 matrix A that satisfies the given conditions, we need to construct a matrix that satisfies each condition individually.
Condition (i) requires that all entries below the main diagonal of A are zero. This condition can easily be satisfied by constructing a matrix with zeros in the appropriate positions.
Condition (ii) states that a18, the entry in the first row and eighth column, must be non-zero. By assigning a non-zero value to this entry, we can fulfill this condition.
Condition (iii) requires that the matrix A is diagonalizable. This condition means that A must have a complete set of linearly independent eigenvectors. If we can find eigenvectors corresponding to distinct eigenvalues that span the entire 8-dimensional space, then A is diagonalizable.
If we are able to construct such a matrix that satisfies all three conditions, we can provide it as an example and prove that it fulfills the given conditions. However, if it is not possible to construct such a matrix, we can prove that no such matrix exists by showing that the conditions are mutually exclusive and cannot be satisfied simultaneously.
Learn more about matrix here:
https://brainly.com/question/29132693
#SPJ11
Please help me!!!!
Liam and Evan are mixing paint. Liam uses 2 quarts of yellow paint and adds 3 1/4 jars of blue paint.
Evan uses 1/2 quart of yellow paint and adds 5 1/2 jars of red paint. They end up with the same volume of paint.

Answers
Answer:
answer is id.k
Step-by-step explanation:
The correct equation to represent the condition is,
⇒ 2 + 3 1/4x = 1/2 + 5 1/2x
And, The volume of the paint is, 2/3 quartz.
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
Liam and Evan are mixing paint. Liam uses 2 quarts of yellow paint and adds 3 1/4 jars of blue paint.
And, Evan uses 1/2 quart of yellow paint and adds 5 1/2 jars of red paint. They end up with the same volume of paint.
Let the volume of the paint is, x
Hence, We can formulate;
The correct equation to represent the condition is,
⇒ 2 + 3 1/4x = 1/2 + 5 1/2x
And, Solve for x as;
⇒ 2 + 13/4x = 1/2 + 11/2x
⇒ 2 - 1/2 = 11/2x - 13/4x
⇒ 3/2 = (44 - 26)x / 8
⇒ 12 = 18x
⇒ x = 12/18
⇒ x = 2/3
Hence, The volume of the paint is, 2/3 quartz.
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ2
Arun is driving on a long road trip. He currently has 9 gallons of gas in his car. Each
hour that he drives, his car uses up 1 gallon of gas. How much gas would be in the
tank after driving for 5 hours? How much gas would be left after t hours?
Gas left after 5 hours:
Gas left after t hours:
Please hurry
Answers
Answer:
9
Step-by-step explanation:
After driving for 5 hours, Arun's car would have used up 5 gallons of gas (1 gallon per hour for 5 hours). Therefore, the amount of gas left in the tank after driving for 5 hours would be 9 gallons - 5 gallons = 4 gallons.
To find the amount of gas left after t hours, we can use the formula:
Gas left after t hours = 9 - (1 x t)
Where t is the number of hours driven.
So, the amount of gas left after t hours would be 9 - t gallons.
After driving for 5 hours, Arun would have 4 gallons of gas left in his tank. If he drives for t hours, he would have (9 - t) gallons of gas left in his tank. The calculations are based on the fact that Arun's car uses 1 gallon of gas per hour of driving.
Explanation:To answer this question, we must understand that Arun's car uses 1 gallon of gas for every hour of driving. So, if he drives for 5 hours, his car will use 5 gallons of gas. Arun starts with 9 gallons of gas, so we subtract the 5 gallons of gas used from the 9 gallons of gas he started with. The result is:
9 - 5 = 4 gallons
So, after driving for 5 hours, Arun would have 4 gallons of gas left in his tank.
Similarly, if he drives for t hours, his car will use t gallons of gas. So, to find how much gas would be left after driving for t hours, we subtract t gallons from the 9 gallons he started with:
9 - t = (9 - t) gallons
Thus, after driving for t hours, Arun would have (9 - t) gallons of gas left in his tank.
Learn more about Fuel Consumption here:https://brainly.com/question/32793205
#SPJ2
Sixty percent of the marbles in a bag are blue. One marble is chosen and replaced. A second marble is chosen and replaced. Then a third marble is chosen. What is the probability that a blue marble will not be chosen?
Answers
Answer:
0.064. same as 8/125
Step-by-step explanation:
Probability is the ratio of the number of possible outcome to the total outcome.
Given that Sixty percent of the marbles in a bag are blue
The probability of picking a blue marble
p(b) = 60% = 3/5
The probability of not picking a blue marble
np(b) = 1 - 60%
= 1 - 3/5
= 2/5
Hence where 3 marbles are picked and replaced, the probability of not picking a blue marble
= 2/5 * 2/5 * 2/5
= 8/125
= 0.064
Aurora is planning to participate in an event at her school's field day that requires her to complete tasks at various stations in the fastest time possible. To prepare for the event, she is practicing and keeping track of her time to complete each station. The x-coordinate is the station number, and the y-coordinate is the time in minutes since the start of the race that she completed the task. (1, 4), (2, 8), (3, 16), (4, 32) Part A: Is this data modeling an arithmetic sequence or a geometric sequence
Answers
The result for the given data are-
Part A: A geometric sequence is being modelled by the data because they share a common ratio = 2.
Part B: The time in which she will complete station 5 calculated by recursive formula is 64 units.
Part C: The time in which she will complete the 9th station calculated by explicit formula 512 units.
What is recursive formula?Any term of a series can be defined by its preceding term in a recursive formula (s).
We learn two things from recursive formulas: the first phrase in the series. The pattern rule states that any term can be derived from its preceding term.
Now, according to the question;
Part A: The data are modeling a geometric sequence since they have a common ratio of 2.
Part B: Use a recursive formula to determine the time she will complete station 5.
f(n)=f(n-1)×r
Where, r is the common difference
f(n)=f(5-1)×2
f(n)=f(4)×2
f(n)=(32)×2 {since, f(4) = 32)}
f(n)= 64
Part C: Use an explicit formula to find the time she will complete the 9th station.
f(n)=f(1)×r^(n-1)
f(n)=4×2^(8-1)
f(n)=4×(2^7)
f(n)=4×128
f(n)=512
To know more about the recursive formula, here
https://brainly.com/question/1275192
#SPJ4
The complete question is -
Aurora is planning to participate in an event at her school's field day that requires her to complete tasks at various stations in the fastest time possible. To prepare for the event, she is practicing and keeping track of her time to complete each station.
The x-coordinate is the station number, and the y-coordinate is the time in minutes since the start of the race that she completed the task.
(1, 4), (2, 8), (3, 16), (4, 32)
Part A: Is this data modeling an arithmetic sequence or a geometric sequence?
Part B: Use a recursive formula to determine the time she will complete station 5.
Part C: Use an explicit formula to find the time she will complete the 9th station.
Answer:
The result for the given data are-
Part A: A geometric sequence is being modelled by the data because they share a common ratio = 2.
Part B: The time in which she will complete station 5 calculated by recursive formula is 64 units.
Part C: The time in which she will complete the 9th station calculated by explicit formula 512 units.
What is recursive formula?
Any term of a series can be defined by its preceding term in a recursive formula (s).
We learn two things from recursive formulas: the first phrase in the series. The pattern rule states that any term can be derived from its preceding term.
Now, according to the question;
Part A: The data are modeling a geometric sequence since they have a common ratio of 2.
Part B: Use a recursive formula to determine the time she will complete station 5.
f(n)=f(n-1)×r
Where, r is the common difference
f(n)=f(5-1)×2
f(n)=f(4)×2
f(n)=(32)×2 {since, f(4) = 32)}
f(n)= 64
Part C: Use an explicit formula to find the time she will complete the 9th station.
f(n)=f(1)×r^(n-1)
f(n)=4×2^(8-1)
f(n)=4×(2^7)
f(n)=4×128
f(n)=512
To know more about the recursive formula, here
brainly.com/question/1275192
#SPJ4
The complete question is -
Aurora is planning to participate in an event at her school's field day that requires her to complete tasks at various stations in the fastest time possible. To prepare for the event, she is practicing and keeping track of her time to complete each station.
The x-coordinate is the station number, and the y-coordinate is the time in minutes since the start of the race that she completed the task.
(1, 4), (2, 8), (3, 16), (4, 32)
Part A: Is this data modeling an arithmetic sequence or a geometric sequence?
Part B: Use a recursive formula to determine the time she will complete station 5.
Part C: Use an explicit formula to find the time she will complete the 9th station.
Explore all similar answers
Step-by-step explanation:
determine whether the geometric series is convergent or divergent. [infinity] (2)n 6n 1 n = 0
Answers
Answer:
To determine whether the geometric series [infinity] (2^n)(6n+1), n=0, is convergent or divergent, we can use the ratio test.
The ratio test states that if the limit of the absolute value of the ratio of the (n+1)th term to the nth term is less than 1, then the series is convergent. If the limit is greater than 1, the series is divergent. If the limit is equal to 1, the test is inconclusive.
Let's apply the ratio test to this series:
|(2^(n+1))(6(n+1)+1)|
--------------------- = |2 * 6n + 13|
|(2^n)(6n+1)|
As n approaches infinity, the absolute value of the ratio simplifies to:
|2 * 6n + 13|
-------------
|2^n|
Dividing both the numerator and denominator by 2^n, we get:
|6n/2^n + 13/2^n|
------------------
1
As n approaches infinity, 6n/2^n approaches 0, and 13/2^n approaches 0. Therefore, the limit of the absolute value of the ratio is 0 + 0 = 0, which is less than 1.
Since the limit of the absolute value of the ratio is less than 1, the series [infinity] (2^n)(6n+1), n=0, is convergent.
Find the 29th term 29,33,37,41
(arithmetic)
Answers
Answer:
a₂₉ = 141
Step-by-step explanation:
The nth term of an arithmetic sequence is
\(a_{n}\) = a₁ + (n - 1)d
where a₁ is the first term and d the common difference
Here a₁ = 29 and d = a₂ - a₁ = 33 - 29 = 4 , then
a₂₉ = 29 + (28 × 4) = 29 + 112 = 141
Answer:
The 29th term of arithmetic sequence is 141.
Step-by-step explanation:
Here's the required formula to find the arithmetic sequence :
\(\longrightarrow{\pmb{\sf{a_n = a_1 + (n - 1)d}}}\)
\(\pink\star\) aₙ = nᵗʰ term in the sequence\(\pink\star\) a₁ = first term in sequence \(\pink\star\) n = number of terms \(\pink\star\) d = common differenceSubstituting all the given values in the formula to find the 29th term of arithmetic sequence :
\(\purple\star\) aₙ = a₂₉\(\purple\star\) a₁ = 29\(\purple\star\) n = 29 \(\purple\star\) d = 4\(\leadsto{\sf{ \: \: a_n = a_1 + (n - 1)d}}\)
\(\leadsto{\sf{ \: \: a_{29} = 29 + (29 - 1)4}}\)
\(\leadsto{\sf{ \: \: a_{29} = 29 + (28)4}}\)
\(\leadsto{\sf{ \: \: a_{29} = 29 + 28 \times 4}}\)
\(\leadsto{\sf{ \: \: a_{29} = 29 + 112}}\)
\(\leadsto{\sf{ \: \: a_{29} = 141}}\)
\(\star \: \: \red{\underline{\boxed{\sf{a_{29} = 141}}}}\)
Hence, the 29th term of arithmetic sequence is 141.
\(\rule{300}{2.5}\)
two of the vertices of a regular octahedron are to be chosen at random. what is the probability that they will be the endpoints of an edge of the octahedron? express your answer as a common fraction.
Answers
In an octahedron, there is a 12/15 = 4/5 chance that two randomly selected vertices will serve as the endpoints of an edge
The term "octahedron" comes from the Greek word which means "8 faced." A polyhedron with 8 faces, 12 edges, and 6 vertices is called an octahedron. Four edges meet at each vertex. One of the five platonic solids with faces that reflect equilateral triangles
Few properties of an octahedron
There are different ways to select 2 of the 6 vertices is:
C(6,2)=6.5/2.1=15
In an octahedron, there is a 12/15 = 4/5 chance that two randomly selected vertices will serve as the endpoints of an edge.
To learn more about Octahedron
https://brainly.com/question/18369918
#SPJ4
Miamor wanted to make note cards by cutting pieces of paper in half.
Before starting she got seven more pieces to use. When she was done she
had 28 half pieces of paper. With how many full pieces did she start?
Answers
Answer: 14 pieces
Step-by-step explanation:
Let the number of pieces of paper she had at first be x.
Before starting she got seven more pieces to use. This can be written as:
= x + 7
When she was done she had 28 half pieces of paper. This can then be written as:
x + 7 = (28 × 1/2)
x + 7 = 14
x = 14 - 7
x = 7
Since x = 7, she started with:
= x + 7
= 7 + 7
= 14 pieces
dr. yung tests a new anti-malaria drug in an asian population and concludes that he cannot reject the null hypothesis, and must conclude he does not have sufficient evidence to conclude that the drug works. in reality, the drug does work. dr. yung has committed a error. group of answer choices logical type i (false positive) type ii (false negative) statistical
Answers
Dr. Yung has committed a type l ( false positive) error.
What is a type I error?Rejecting a null hypothesis that is actually true in the population results in a type I error (false-positive); failing to reject a null hypothesis that is actually false in the population results in a type II error (false-negative).
A type I error occurs when a null hypothesis that is actually true is mistakenly rejected during statistical hypothesis testing (also known as a "false positive" finding or conclusion; example: "an innocent person is convicted"),
Therefore, the error is a type 1 error.
Learn more about type 1 error on:
https://brainly.com/question/28166129
#SPJ1
Graph r < -9 on number line
Answers
Graph r < -9 on number line???
Step-by-step explanation:
ayusin nyu po tanung nyuh lods
If f(x) = 2x2 - 9, find f(5).
Answers
Find A and C for both questions

Answers
true or false: double integral can be used to compute the area of a region d in a plane simply by integrating the function f(x,y)
Answers
True. The double integral can be used to compute the area of a region d in a plane by integrating the function f(x,y). In fact, the double integral of f(x,y) over a region D in the xy-plane gives the volume of the solid between the surface z=f(x,y) and the xy-plane over the region D.
However, if we take the function f(x,y) to be the constant function 1, then the double integral of f(x,y) over the region D is simply the area of the region D. Therefore, we can compute the area of a region D in a plane by integrating the constant function 1 over the region D using the double integral. Integrating over two variables requires calculating two separate integrals, so the answer is more than 100 words.
True. A double integral can be used to compute the area of a region D in a plane by integrating the function f(x, y). To find the area, you would integrate the function f(x, y) = 1 over the region D, as the double integral represents the sum of the function values over the entire area. The double integral can be thought of as a generalization of single-variable integration, allowing us to find the area in two dimensions.
To know more about Area visit:
https://brainly.com/question/13194650
#SPJ11
(co 3) sixty-seven percent of adults have looked at their credit score in the past six months. if you select 29 customers, what is the probability that at least 25 of them have looked at their score in the past six months?
Answers
The probability that at least 25 of the 29 customers have looked at their credit score in the past six months is:
P(X ≥ 25) = sum(P(X = i)) i = 25 to 29
Binomial Credit Score ProbabilityThis is a question of probability and statistics, specifically in the area of binomial distributions. The probability of a single event can be calculated using the binomial probability formula:
P(X = k) = (n choose k) * p^k * (1-p)^(n-k)
Where:X = the number of successful outcomes (in this case, the number of customers who have looked at their credit score in the past six months)
k = the number of successful outcomes we want to know the probability of (in this case, 25)
n = the total number of trials or customers (in this case, 29)
p = the probability of a successful outcome (in this case, 0.67 or 67%)
To find the probability that at least 25 of the 29 customers have looked at their credit score in the past six months, we will need to use the cumulative binomial probability formula which isP(X ≥ k) = sum(P(X = i)) i = k to n
So the probability that at least 25 of the 29 customers have looked at their credit score in the past six months isP(X ≥ 25) = sum(P(X = i)) i = 25 to 29
Learn more about Binomial Probability here:
https://brainly.com/question/11608176
#SPJ4
HELP DUEEE TONIGHT!!!!!
a group of 175 adults were asked whether they exercise and whether they are vegetarian. their responses are summarized in the following table.

Answers
a) 44%
b) 40%
c) 28%
d) either one of the no's.
XD XD XD I need help

Answers
Answer:
27 cubic units
Step-by-step explanation:
Volume = length*width*height, or lwh. Since the lwh of this cube is 3*3*3, multiply to get 27.
Answer:
27
Step-by-step explanation:
i multiplied.
A public Interest group conducts a poll of 750 Randomly selected American households and finds that 67% of those surveyed have at least one dog.
a) construct and interpret a 90% confidence interval for the proportion of all American households who have at least one dog.
b) Explain what is meant by 90% confidence in this context
Answers
a. The 90% confidence interval for the proportion of all American households who have at least one dog is (0.636, 0.704). This means we can be 90% confident that the true proportion of all American households who have at least one dog lies within this range.
b. The 90% confidence means that if we were to repeat this poll many times with different samples of American households, we would expect 90% of the resulting confidence intervals to contain the true proportion of all American households who have at least one dog
a) To construct a 90% confidence interval for the proportion of all American households who have at least one dog, we can use the following formula:
CI = p ± zsqrt((p(1-p))/n)
where:
CI is the confidence interval
p is the sample proportion (67% or 0.67 in decimal form)
z is the z-score corresponding to the level of confidence (90% or 1.645 for a one-tailed test)
n is the sample size (750)
Plugging in the values, we get:
CI = 0.67 ± 1.645sqrt((0.67(1-0.67))/750)
CI = 0.67 ± 0.034
Therefore, the 90% confidence interval for the proportion of all American households who have at least one dog is (0.636, 0.704). This means we can be 90% confident that the true proportion of all American households who have at least one dog lies within this range.
b) In this context, 90% confidence means that if we were to repeat this poll many times with different samples of American households, we would expect 90% of the resulting confidence intervals to contain the true proportion of all American households who have at least one dog.
In other words, we can be reasonably sure that our sample proportion of 67% is a good estimate of the true proportion, with a margin of error of about 3.4 percentage points, based on the sample size and the level of confidence we have chosen.
Learn more about confidence interval at https://brainly.com/question/23411442
#SPJ11
What are two differnt ways of factoring -3x-9?
Answers
Answer:
\(-3(x+3)\)
Factor the expression
\(-3x-9\)
\(-3(x+3)\)
I hope this helps you :D
Answer:
Hello
Step-by-step explanation:
Two different ways are:
–3(x + 3) & 3(–x – 3)
Hope this helps, please give me an brainliest
small brainnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Answers
Answer:
combined means to add so you are going to add anything over 1 because it says longer than 1
1 1/4 has 2 marks so you add 1 1/4 + 1 1/4 =
they have like denominators so you can add them together
1 + 1 = 2 and 1/4 + 1/4 = 2/4 which can be reduced to 1/2
so your answer is 2 1/2
HEKP PLEASE; what is movement competence ?
1 when we move in safe manner
2 when we move with confidence
3 when our movement is effective
4 all the above
Answers
Answer:
I think its maybe 2 you might want to check tho
Find the volume of the solid. PLEASE HELPPPPPPPP

Answers
Answer:
V≈743.25
Step-by-step explanation:
V=5
12tan(54°)ha2=5
12·tan(54°)·4·182≈743.24624
can someone help me with this

Answers
Answer:
1. 40 members
2. 4 cheerleaders
3. 40 marbles
4. 2 marbles
5. 8
6. 24
Step-by-step explanation:
1. cross multiply 12/x=30/100
2. cross multiply 12/x=10/100
3. 18/x=45/100
4. x/40=5/100
5. we know 5% is 2 marbles. multiply by 4 to get 8 marbles.
6. 20%=8 marbles. 60/20= 3. 3 x 8= 24 marbles.
Solve for h in the figure below

Answers
Answer:
b. \(\frac{2}{3} \: ft\)
Step-by-step explanation:
\( \triangle ABE\sim \triangle CDE\)
(AA postulate)
\( \therefore \frac{AB}{CD} =\frac{BE}{DE} \)
\( \therefore \frac{2}{h} =\frac{24}{8} \)
\( \therefore \frac{2}{h} =3 \)
\( \therefore h= \frac{2}{3} \: ft\)