Which of the following is the inverse relation of the set?{(3, 1), (4, 2), (5, 3), (6, 4)}Question 4 options:A) {(2, 4), (3, 3), (5, 4), (6, 1)}B) {(2, 1), (4, 3), (5, 3), (6, 4)}C) {(1, 3), (2, 4), (3, 5), (4, 6)}D) {(3, 1), (4, 2), (5, 3), (6, 4)}
Answers
Given the set:
{(3, 1), (4, 2), (5, 3), (6, 4)}
Let's determine the inverse relation of the set.
For a point: (a, b), the inverse of the function will have the point (b, a).
Therefore, the inverse of the pairs are:
(3, 1) ==> (1, 3)
(4, 2) ==> (2, 4)
(5, 3) ==> (3, 5)
(6, 4) ==> (4, 6)
Hence, the relation which shows the inverse of the set is:
{(1, 3), (2, 4), (3, 5), (4, 6)}
ANSWER:
C) {(1, 3), (2, 4), (3, 5), (4, 6)}
Related Questions
(a) Write a formula for the distance between the points (x,y) and (4,6)
(b) If the distance
between above points is 9 units, write an equation.
Answers
(B). X²+y²-8x-12y-29=0.
(a) What is Distance Between Two Points Formula? Distance between two points is the length of the line segment that connects the two points in a plane. The formula to find the distance between the two points is usually given by
d=√((x2 – x1)² + (y2 – y1)²)
The point for (X1,y1) is (x,y).
And the point for (x2,y2) is (4,6)
d = √((4-x)²+(6-y)²)
(B). It is given that
Distance between above equation is 9 units.
So d=9.
√((4-x²)+(6-y²)) = 9
((4-x)²+(6-y)²) = 81
(16+x²-8x)+(36+y²-12y)=81
Now we have to calculate this equation.
We can write this equation as,
16+36+x²+y²-8x-12y=81
52+x²+y²-8x-12y=81
X²+y²-8x-12y=81-52
X²+y²-8x-12y=29
X²+y²-8x-12y-29=0.
So,this is the equation for distance = 9 units.
To know more about Cartesian coordinates
Visit:. brainly.com/question/4126140
#SPJ9
80 years converted to sec
Answers
Answer: 2522880000 seconds
Step-by-step explanation:
80(365) = 29200 days
29200(24) = 700800 hours
700800(60) = 42048000 minutes
42048000(60) = 2522880000 seconds
Answer:
2522880 000 is the answer
What is the answer pleaseee

Answers
Answer: 803.84cm3
Step-by-step explanation:
The formula for finding the volume of a cylinder is πr2h.
In other words, the area of the top face's circle times the height.
To find the circle's area, we first find the radius of the circle. Since the diameter is 8cm, we divide by 2 to get the radius, which is 4cm.
4cm squared is 4cm x 4cm, which is 16cm. 16cm times 3.14 is 50.24cm squared.
Now, we have the area of the circle. 50.24cm squared!
The height is 16cm, so to find the cylinder, we times the area of the circle by the height of the cylinder! So,
16cm x 50.24cm squared = 803.84cm cubed.
The volume of the can of soup is 803.84cm cubed.
The equation y=-3x² describes a parabola. Which way does the parabola open?
A. Left
B. Right
C. Up
D. Down

Answers
Angle ABC And BCA a are complementary angle ABC is 85° if angle BCA is named as 3b -7 what could be the value of b?
Answers
Therefore,
angle ABC + angle BCA = 90
But, angle BCA = 3b - 7
and angle ABC = 85
Therefore,
85 + 3b - 7 = 90
3b - 7 = 5
3b = 12
b = 4
Of the six members in the Spirit of Woodstock rock band, four can play guitar. There are three who can play keyboards. All of the singers play guitar, and two of the guitarists also play keyboards. Two members do all three. One guitarist doesn’t sing. How many members sing but do not play keyboards?
Answers
Answer:
1 can sing but cannot play keyboard.
Step-by-step explanation:
There are six members in the rock band. We need to identify how many person can sing, play guitar and play keyboard. To identify this we will find out number of member for each activity,
Total 6 members
4 can play guitar
3 can pay keyboard
All singers play guitar but one guitarist cannot sing.
There will be 1 singer who cannot play keyboard.
In cricket, one over consists of 6 balls being bowled. Determine the number of overs bowled if 120 balls are bowled. it form (2)
Answers
Based on the proportionate ratios of 1:6, the number of overs bowled if 120 balls are bowled is 20.
What is proportion?Proportion describes two ratios equated to each other.
Proportional values are like fractional values and can be depicted in percentages or fractions.
The ratio of one over and balls bowled = 1:6
This implies that for every 6 balls being bowled, one goes over.
Proportionately, for 120 balls bowled, the number of overs will be = 20 (120/6 x 1)
Thus, if one over consists of 6 balls being bowled, proportionately, the number of overs bowled if 120 balls are bowled is 20.
Learn more about proportions at https://brainly.com/question/1496357.
#SPJ1
Pls help!
Whoever answers in a few minutes with a clear answer will be marked brainiest!!!
Use exponent laws to write each expression with a positive power

Answers
Answer:
a. \(\tt \frac{1}{9}\)
b. \(\frac{1}{16}\)
c. 4
Step-by-step explanation:
\(\tt a. \:3^{-2}\)
We can use the negative exponent rule, which states that \(\boxed{\tt a^{-n} = \frac{1}{a^n}}\) So, we have:
\(\tt 3^{-2} = \frac{1}{3^2} = \frac{1}{9}\)
\(\hrulefill\)
\(\tt b.\: -2^{-4}\)
We can use the rule that \(\boxed{\tt -a^{-n} = (-1)^n \cdot a^n}.\) So, we have:
\(\tt -2^{-4} = (-1)^4 \cdot 2^{-4} = 1 \cdot \frac{1}{2^4} = \frac{1}{16}\)
\(\hrulefill\)
\(\tt c. \:(\frac{1}{2})^{-2}\)
We can use the negative exponent rule, which states that \(\boxed{\tt a^{-n} = \frac{1}{a^n}}\). So, we have:
\(\tt (\frac{1}{2})^{-2} = \frac{1}{(\frac{1}{2})^2} = \frac{1}{\frac{1}{4}} = 4\)
Answer:
Step-by-step explanation:
(a) 3^-2 = 1/9
(b) (-2)^-4 = 1/(-2)^4 = 1/16
(c) (1/2)^-2 = 1/(1/2)^2=1 / 1/4 = 4
Which expression is equivalent to 9x²-2y+3x²-3y?
O 6x²+6x²-6y
O 6x²+3x²-5y
O 12x²-2y-3y
O 12x²+2y-3y
Answers
Answer: 12x²-2y-3y ==> Option 3
Step-by-step explanation:
9x²-2y+3x²-3y=
9x²+3x²-2y-3y=
12x²-5y=
12x²-2y-3y ==> Option 3
100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answers
The length KL is 8 units
The value of x is undefined
The length KL is 12 units
Calculating the length KLFrom the question, we have the following parameters that can be used in our computation:
The rhombus
Also, we have
DK = 8
A rhombus is a quadrilateral with all sides equal.
So, we have
KL = 8
Calculating the value of xHere, we have
SKAL = 2x - 8
There is no point S on the rhombus
This means that
x = undefined
Calculating the length KLHere, we have
DM = 5y + 2 and DK = 3y + 6
A rhombus is a quadrilateral with all sides equal.
So, we have
5y + 2 = 3y + 6
Evaluate
2y = 4
Divide
y = 2
So, we have
KL = 5 * 2 + 2
KL = 12
Hence, the length KL is 12 units
Read more about rhombus at
https://brainly.com/question/12735921
#SPJ1
write the numeral of twelve Arab sixty core
Answers
Answer:
12600000000
Step-by-step explanation:
write the numeral of twelve Arab sixty core
The numeral of twelve Arab sixty core is
=> 12600000000
hope it is helpful to you
Step-by-step explanation:
the numeral from is 12600000000
-3(5x-9)=??????????????
Answers
Answer:
=−15x+27
Step-by-step explanation:
OK LET ME EXPLAIN :3
First what I would do is -3 x -9 which would be a 27 (Negative x Negative = Positve)
Then I would do 27 x 5 which is 135
Answer: 135
There ya go hope this helped!!
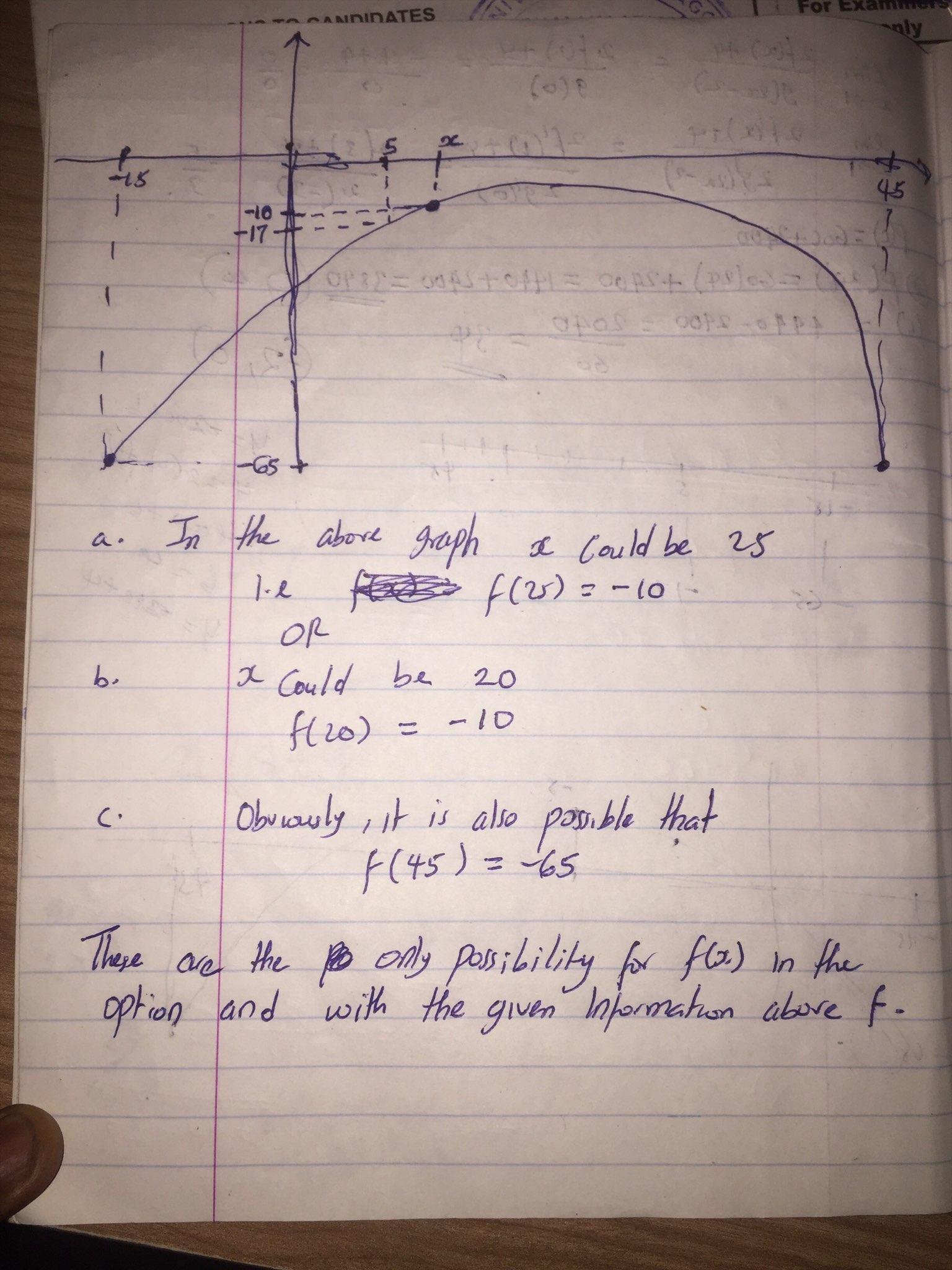
would you please answer the following image that i upload

Answers
Given
\(\begin{gathered} \text{Domain -15}\leq x\leq45 \\ \text{Range -65}\leq f(x)\leq-5 \end{gathered}\)\(\begin{gathered} f(5)=-17 \\ f(-15)=-65 \end{gathered}\)The final answer
\(\begin{gathered} f(25)=-10 \\ f(20)=-10 \\ f(45)=-65 \end{gathered}\)
Given the function f(x) = 0.5|x - 41-3, for what values of x is f(x) = 7?
x = -24, x = 16
x= -16, x = 24
x=-1, x = 9
x = 1, x = -9
Answers
The values of x for which f(x) = 7 are x = 61 and x = 21.
To find the values of x for which f(x) = 7, we can set up the equation and solve for x.
The given function is f(x) = 0.5|x - 41| - 3.
Setting f(x) equal to 7, we have:
0.5|x - 41| - 3 = 7.
First, let's isolate the absolute value term:
0.5|x - 41| = 7 + 3.
0.5|x - 41| = 10.
To remove the absolute value, we can consider two cases:
Case: (x - 41) is positive or zero:
0.5(x - 41) = 10.
Multiplying both sides by 2 to get rid of the fraction:
x - 41 = 20.
Adding 41 to both sides:
x = 61.
So x = 61 is a solution for this case.
Case: (x - 41) is negative:
0.5(-x + 41) = 10.
Multiplying both sides by 2:
-x + 41 = 20.
Subtracting 41 from both sides:
-x = -21.
Multiplying both sides by -1 to solve for x:
x = 21.
So x = 21 is a solution for this case.
Therefore, the values of x for which f(x) = 7 are x = 61 and x = 21.
for such more question on values
https://brainly.com/question/11546044
#SPJ8
How would you set up question 4

Answers
Step-by-step explanation:
please mark me as brainlest

Step-by-step explanation:
hope it's helpful for you
pls mark above guy ans as brainliest

a line parrell to y=5x+9 and intersects the point (-2,-3). What is the equation of this parrell line
Answers
Answer:
\(y - 5x = 4\)
Step-by-step explanation:
\(y = 5x + 9 \\ m1 = 5 \\ since \: the \: line \: is \: parallel \: m1 = m2 \\ y - y1 = m(x - x1) \\ y - ( - 3) = 5(x - ( - 2)) \\ y + 4 = 5(x + 2) \\ y + 4 = 5x + 10 \\ y - 5x = 10 - 6 \\ y - 5x = 4\)
The temperature in a hotel is 21 °C.
The temperature in the hotel is 26,7°C warmer than at the top of the mountain.
The temperature at the top of the mountain is 3.2°C colder than at the bottom of the mountain.
Work out the temperature at the bottom of the mountain.
Answers
The temperature at the bottom of the mountain is 50.9 °C.
Let's work through the given information step by step to find the temperature at the bottom of the mountain.
The temperature in the hotel is 21 °C.
The temperature in the hotel is 26.7 °C warmer than at the top of the mountain.
Let's denote the temperature at the top of the mountain as T_top.
So, the temperature in the hotel can be expressed as T_top + 26.7 °C.
The temperature at the top of the mountain is 3.2 °C colder than at the bottom of the mountain.
Let's denote the temperature at the bottom of the mountain as T_bottom.
So, the temperature at the top of the mountain can be expressed as T_bottom - 3.2 °C.
Now, let's combine the information we have:
T_top + 26.7 °C = T_bottom - 3.2 °C
To find the temperature at the bottom of the mountain (T_bottom), we need to isolate it on one side of the equation. Let's do the calculations:
T_bottom = T_top + 26.7 °C + 3.2 °C
T_bottom = T_top + 29.9 °C
Since we know that the temperature in the hotel is 21 °C, we can substitute T_top with 21 °C:
T_bottom = 21 °C + 29.9 °C
T_bottom = 50.9 °C
Therefore, the temperature at the bottom of the mountain is 50.9 °C.
for such more question on temperature
https://brainly.com/question/14820864
#SPJ8
Use the limit comparison test to determine whether ∑n=19∞an=∑n=19∞8n3−2n2+196+3n4 converges or diverges.
(a) Choose a series ∑n=19∞bn with terms of the form bn=1np and apply the limit comparison test. Write your answer as a fully simplified fraction. For n≥19,
limn→∞anbn=limn→∞
(b) Evaluate the limit in the previous part. Enter ∞ as infinity and −∞ as -infinity. If the limit does not exist, enter DNE.
limn→∞anbn =
(c) By the limit comparison test, does the series converge, diverge, or is the test inconclusive?

Answers
Answer:
Diverges
General Formulas and Concepts:
Algebra I
Exponential Rule [Dividing]: \(\displaystyle \frac{b^m}{b^n} = b^{m - n}\)Calculus
Limits
Limit Rule [Variable Direct Substitution]: \(\displaystyle \lim_{x \to c} x = c\)Series Convergence Tests
P-Series: \(\displaystyle \sum^{\infty}_{n = 1} \frac{1}{n^p}\)Direct Comparison Test (DCT)Limit Comparison Test (LCT): \(\displaystyle \lim_{n \to \infty} \frac{a_n}{b_n}\)Step-by-step explanation:
Step 1: Define
Identify
\(\displaystyle \sum^{\infty}_{n = 19} \frac{8n^3 - 2n^2 + 19}{6 + 3n^4}\)
Step 2: Apply DCT
Define Comparison: \(\displaystyle \displaystyle \sum^{\infty}_{n = 19} \frac{n^3}{n^4}\)[Comparison Sum] Simplify: \(\displaystyle \displaystyle \sum^{\infty}_{n = 19} \frac{1}{n}\)[Comparison Sum] Determine convergence: \(\displaystyle \displaystyle \sum^{\infty}_{n = 19} \frac{1}{n} = \infty , \ \text{div by P-Series}\)Set up inequality comparison: \(\displaystyle\frac{8n^3 - 2n^2 + 19}{6 + 3n^4} \geq \frac{1}{n}\)[Inequality Comparison] Rewrite: \(\displaystyle n(8n^3 - 2n^2 + 19) \geq 6 + 3n^4\)[Inequality Comparison] Simplify: \(\displaystyle 8n^4 - 2n^3 + 19n \geq 6 + 3n^4 \ \checkmark \text{true}\)∴ the sum \(\displaystyle \sum^{\infty}_{n = 19} \frac{8n^3 - 2n^2 + 19}{6 + 3n^4}\) is divergent by DCT.
Step 3: Apply LCT
Define: \(\displaystyle a_n = \frac{8n^3 - 2n^2 + 19}{6 + 3n^4}, \ b_n = \frac{1}{n}\)Substitute in variables [LCT]: \(\displaystyle \lim_{n \to \infty} \frac{8n^3 - 2n^2 + 19}{6 + 3n^4} \cdot n\)Simplify: \(\displaystyle \lim_{n \to \infty} \frac{8n^4 - 2n^3 + 19n}{6 + 3n^4}\)[Limit] Evaluate [Coefficient Power Rule]: \(\displaystyle \lim_{n \to \infty} \frac{8n^4 - 2n^3 + 19n}{6 + 3n^4} = \frac{8}{3}\)∴ Because \(\displaystyle \lim_{n \to \infty} \frac{a_n}{b_n} \neq 0\) and the sum \(\displaystyle \sum^{\infty}_{n = 19} a_n\) diverges by DCT, \(\displaystyle \sum^{\infty}_{n = 19} \frac{8n^3 - 2n^2 + 19}{6 + 3n^4}\) also diverges by LCT.
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Convergence Tests (BC Only)
Book: College Calculus 10e
True or false?
Barriers that keep a business from entering a market can lead to perfect competition.
Answers
Answer: true
Step-by-step explanation:
leads to a monopoly
Suppose that the distribution of monthly revenues of a new startup business is not symmetric.
According to Chebyshev's Theorem, at least approximately what percentage of the revenues are within k=3.3 standard deviations of the mean?
Answers
According to Chebyshev's Theorem, approximately 91% of the revenues are within k = 3.3 standard deviations of the mean.
What is Chebyshev's Theorem?
The minimum percentage of observations that are within a given range of standard deviations from the mean is calculated using Chebyshev's Theorem. Several other probability distributions can be applied to this theorem. Chebyshev's Inequality is another name for Chebyshev's Theorem. For a large class of probability distributions, Chebyshev's inequality ensures that no more than a specific percentage of values can deviate significantly from the mean.
According to Chebyshev's Theorem, at least 1 - 1/k² of the revenues lie within k standard deviations of the mean.
So when k = 3.3
1 - 1/k² = 1 - 1/3.3² = 1 - 0.0918 = 0.9082 = 90.82% ≈ 91%
Therefore according to Chebyshev's Theorem, approximately 91% of the revenues are within k = 3.3 standard deviations of the mean.
To learn more about Chebyshev's Theorem, follow the link.
https://brainly.com/question/5179184
#SPJ1
least common number
( sorry i forgot what its called )
of 598 and 45
Answers
The least common multiple of 598 and 45 is 26, 910
How to find the least common multiple ?To find the least common multiple of 598 and 45, you can use the prime factorization method. This involves finding the prime factors of both 598 and 45 and then multiplying these prime factors when they are in their highest power.
This gives:
598 prime factorization :
2 x 13 x 23 = 598
45 prime factorization :
3 x 3 x 5 = 45
The least common multiple is;
= 2 x 13 x 23 x 3 x 3 x 5
= 26, 910
Find out more on least common multiple at https://brainly.com/question/233244
#SPJ1
Write an equivalent expression by distributing the "
"sign outside the parentheses:
-(0.3h + 4k –3
Answers
Hi there!
»»————- ★ ————-««
I believe your answer is:
\(-0.3h-4k+3\)
»»————- ★ ————-««
Here’s why:
⸻⸻⸻⸻
\(-(0.3h+4k-3)\\------------\\-1 * 0.3h = -0.3h\\\\-1 * 4k = -4k\\\\-1 * -3 = 3\\\\\\-(0.3h+4k - 3) \rightarrow \boxed{-0.3h-4k +3}\)
⸻⸻⸻⸻
»»————- ★ ————-««
Hope this helps you. I apologize if it’s incorrect.
find the missing side. round to the nearest tenth

Answers
The required angle is 24.5°.
Given is a right triangle with perpendicular side 16 and the base = 35 we need to find an acute angle in it,
To find the acute angle in a right triangle given the lengths of the perpendicular side and the base, you can use the tangent function.
The tangent of an angle is defined as the ratio of the length of the perpendicular side to the length of the base side.
In this case, the perpendicular side is 16 and the base is 35.
Let's denote the acute angle as θ.
Using the tangent function, we can set up the equation:
tan(θ) = perpendicular side / base
tan(θ) = 16 / 35
To find the value of θ, we can take the inverse tangent of both sides:
θ = tan⁻¹(16 / 35)
θ = 24.5°
Hence the required angle is 24.5°.
Learn more about tangent function, click;
https://brainly.com/question/28994024
#SPJ1
The table shows the number of apples and the total weight of the apples estimate the weight of 6 apples

Answers
Answer:
6 apples will weigh about 1,533 grams
Step-by-step explanation:
Set up an equation:
2
Variable x = weight of 6 apples
2/511 = 6/x
Cross multiply
2 × x = 511 × 6
2x = 3066
Divide both sides by 2
x = 1533
Check your work
2/511 = 6/1533
2 × 1533 = 511 × 6
3066 = 3066
Correct
Pls help I need help on this question

Answers
Answer: B
Step-by-step explanation: Hope this helps:)
HELP ME PLEASEEEE INSTANTLY

Answers
The solution of the given inequality is -2(2/3) < c < 5 (1/3) which is the first option.
We are given the inequality:-
I3c - 4I < 12
We have to find the solution of the given inequalities.
Let 3c - 4 ≥ 0
Hence,
3c - 4 < 12
3c < 16
c < 16/3 = 5 (1/3)
c < 5 (1/3)
Let 3c - 4 < 0
Hence,
-3c + 4 < 12
-8 < 3c
-8/3 = -2(2/3) < c
-2(2/3) < c
Hence, we can write,
-8/3 = -2(2/3) < c
-2(2/3) < c < 5 (1/3)
Hence, the solution is Option A.
To learn more about inequality, here:-
https://brainly.com/question/28823603
#SPJ1
i need help asap please

Answers
Answer:
A, D, and F
Step-by-step explanation:
Tiara did multiply and regroup correctly in the first partial product. Tiara did not multiply and regroup correctly in the second partial product. Tiara was not correct when she added her 2 partial products.
Tiara should of got 18,291 but instead she got 16,291.
When she went to the part to multiply 3x4 she didn't add the remaining 2 from the 3x6+2. So if she did 3x4+2 she would of got the number 14 instead of 12 to put down in the second partial product. Which would make the addition part of it as 4,221 + 14070 = 8291 instead of 4,221 + 12,071 = 16, 291
I hope you understand :)
There are 24 seats in each row of the middle school auditorium.
The table shows the number of students from each grade who
attended a concert. If the students fill each row in the auditorium,
how many rows would be needed for all of the students?
Grade
Number of Students
Sixth
310
Seventh
256
Eighth
262
Answers
Answer:
34.5
Step-by-step explanation:
310 +256 +262= 810
810÷24=34.5
Find the greatest common factor of 10b³ and 4b.
Answers
Solution:
2b would be the greatest common factor (GCF) between both 10b^3 and 4b.
Hope this helps!
PLEASE ANSWER ASAP!!!!!

Answers
Answer:
\(\huge\boxed{\sf r = 5}\)
Step-by-step explanation:
Given that,
7(q + 5) = (q + r)7Distribute7q + 35 = 7q + 7r
Subtract 7q from both sides7q - 7q + 35 = 7q - 7q + 7r
35 = 7r
Divide both sides by 735/7 = r
5 = r
OR
r = 5\(\rule[225]{225}{2}\)
Answer:
r = 5
Step-by-step explanation:
Given statement,
→ 7(q + 5) is equivalent to (q + r)7.
Forming the equation,
→ 7(q + 5) = 7(q + r)
Now we have to,
→ Find the required value of r.
Then the value of r will be,
→ 7(q + 5) = 7(q + r)
Applying Distributive property:
→ 7(q) + 7(5) = 7(q) + 7(r)
→ 7q + 35 = 7q + 7r
Cancelling 7q from both sides:
→ 35 = 7r
→ 7r = 35
Dividing the RHS with number 7:
→ r = 35/7
→ [ r = 5 ]
Therefore, the value of r is 5.