Answers
Answer:
Can I see/view the picture of option 3?
Step-by-step explanation:
Related Questions
The base of a solid is bounded by y=x,y=0, and x=1. Find the volume of the solid for each of the following cross sections (taken perpendicular to the y-axis): (a) squares, (b) semicircles, (c) equilateral triangles, and (d) semi ellipses whose heights are twice the lengths of their bases.
Answers
To find the volume of the solid, you need to calculate the area of each cross-section and then multiply that by the thickness of the section (which is the distance along the y-axis).
(a) Squares: The cross-sections are squares with sides of length y. The area of a square is side^2, so the area of each square is y^2. The thickness of the section is the distance along the y-axis, which is the difference between y and 0, or simply y. So the volume of the solid for each of the square cross-sections is y^2 * y
(b) Semicircles: The cross-sections are semicircles with radii of length y. The area of a semicircle is (pi * r^2) / 2 , so the area of each semicircle is (pi * y^2) / 2. The thickness of the section is the distance along the y-axis, which is the difference between y and 0, or simply y. So the volume of the solid for each of the semicircular cross-sections is (pi * y^2) / 2 * y
(c) Equilateral triangles: The cross-sections are equilateral triangles with side length of y. The area of an equilateral triangle is (s^2 * √3)/4. so the area of each equilateral triangle is (y^2 * √3) / 4. The thickness of the section is the distance along the y-axis, which is the difference between y and 0, or simply y. So the volume of the solid for each of the equilateral triangle cross-sections is (y^2 * √3) / 4 * y
(d) Semi-ellipses: The cross-sections are semi-ellipses whose heights are twice the lengths of their bases. The area of a semi-ellipse is πab/2, where a and b are the lengths of the semi-major and semi-minor axes respectively. Therefore the area of each semi-ellipse will be (πy^2)/2. The thickness of the section is the distance along the y-axis, which is the difference between y and 0, or simply y. So the volume of the solid for each of the semi-ellipse cross-sections is (πy^3)/2
It is important to note that this is a theoretical volume calculation, as the shape of the solid does not have a closed form representation by these functions, but rather, these are an approximation.
Also, for any of these volumes to be meaningful, we have to integrate over the range of the variable y, since it is bounded by the equations y=x, y=0 and x=1, the variable y is limited.
To know more about volume of the solid refer to:
brainly.com/question/21036176
#SPJ4
A zip wire runs between two posts, 25m apart. The zip wire is at an angle of 10 degrees to the horizontal. Calculate the length of the zip wire.
∘
to the horizontal. Calculate the length of the zip wire
Answers
The length of the zip wire, with a 10-degree angle to the horizontal and a distance of 25 meters between the posts, is approximately 25.35 meters.
To calculate the length of the zip wire, we can use trigonometry. Let's consider the triangle formed by the zip wire, where the horizontal distance between the two posts is 25 meters and the angle between the zip wire and the horizontal is 10 degrees.
Using trigonometric functions, we can determine the length of the zip wire. In this case, we'll use the sine function because we have the opposite side (the vertical distance) and we want to find the hypotenuse (the length of the zip wire).
The formula for sine is:
sin(angle) = opposite / hypotenuse
Rearranging the formula, we have:
hypotenuse = opposite / sin(angle)
In this case, the opposite side is the vertical distance, which is h.
So, the formula becomes:
hypotenuse = h / sin(angle)
To find h, we can use the formula for the length of the zip wire:
h = 25 * tan(angle)
Substituting this into the previous formula, we get:
hypotenuse = (25 * tan(angle)) / sin(angle)
Calculating the value, we have:
hypotenuse = (25 * tan(10°)) / sin(10°)
Using a calculator, we find:
tan(10°) ≈ 0.1763
sin(10°) ≈ 0.1736
Substituting these values, we can calculate the length of the zip wire:
hypotenuse ≈ (25 * 0.1763) / 0.1736 ≈ 25.35 meters
Therefore, the length of the zip wire is approximately 25.35 meters.
For more question on length visit:
https://brainly.com/question/28322552
#SPJ8
Help Quickly! A truck needs 7 gallons of fuel to travel 56 miles. Can the truck travel 48 miles with 6 gallons of fuel? Explain.
Giving brainliest

Answers
Yes, 7/56 and 6/48 are proportional because 7×48 = 56×6. Therefore, the correct answer is option B.
Given that, a truck needs 7 gallons of fuel to travel 56 miles.
The truck travel 48 miles with 6 gallons of fuel.
Here, the proportion is
7:56::6:48
We know that, the proportion is product of extremes = product of means
7×48 = 56×6
336 = 336
Therefore, the correct answer is option B.
To learn more about the proportional relationship visit:
brainly.com/question/12917806.
#SPJ1
Suppose that x and y vary inversely, and x = 30 when y = 2. Find y when x=5.
Answers
Answer:
Step-by-step explanation:
1. x is inversely proportional to y
x=k/y
k is the constant of proportionality
x =60/y
2. x=60/y
x=60/12
x=5
What is the domain of this function ?

Answers
Ciana earns an hourly wage of $30 at her job. In order to purchase her sneakers she will have to take time off work, so each hour away from her job
costs her $30 in lost Income. Assume that ciana travel time is the same each way (to and from the store) and that it will take her 30 minutes once
she reaches a store to complete her shopping. Assume throughout the question that ciara incurs no additional costs other than the sneakers, such as
gas.
complete the following table by computing the opportunity cost of ciana’s time and the total cost of shopping at each location

Answers
Ciana should purchase the skirt at the store across town because the total economic cost will be lowest.
How to determine the opportunity cost?Ciana makes $30 per hour at her work, and her purchase decision includes the opportunity cost of lost wages:
Total economic cost:
Local store = $114 + [1/4 hours x 2 (round trip) x $30] + (1/2 hours x $30 spent shopping) = $144
Across town = $86 + [1/2 hours x 2 (round trip) x $30] + (1/2 hours x $30 spent shopping) = $131
Neighboring city = $60 + [1 hour x 2 (round trip) x $30] + (1/2 hours x $30 spent shopping) = $135
Ciana should buy a skirt at the store across town. Because it has the lowest total economic cost ($131).
Opportunity cost is the lost benefit or additional cost of choosing one activity or investment over another. Economic costs include both accounting costs and opportunity costs.
Read more about Opportunity Cost at: https://brainly.com/question/1549591
#SPJ1
The dividen is greater that 1,000, The quotient of 52 with a remainder of 18
Answers
The minimum divisor such that the dividend is greater than 1000 and a quotient of 52 with a remainder of 18 is 18.86.
What is the arithmetic operator?Arithmetic operators are four basic mathematical operations in which summation, subtraction, division, and multiplication involve.,
Division = divide any two numbers or variable called division.
Let's consider a division problem.
5/2 → 2 + 1
Here 5 is called the dividend,2 is the divisor,2 is the quotient, and 1 is the remainder.
Now,
2 × 2 + 1 = 5
Therefore,divisor × quotient + remainder = dividend
So,
Let's suppose the divisor in the given case is x
Now,
52x + 18 ≥ 1000
52x ≥ 982
x ≥ 18.86
Hence "The minimum divisor such that the dividend is greater than 1000 and a quotient of 52 with a remainder of 18 is 18.86".
To learn more about the arithmetic operators,
brainly.com/question/25834626
#SPJ1
The given question is incomplete complete question is ;
What is the minimum divisor such that The dividend is greater than 1,000, The quotient of 52 with a remainder of 18
Two glasses of milk and three snack bars have a total of 72 carbs. and 4 glasses of milk and 2 snack bars have a total of 88 carbs. Determine how many carbs are one glass of mild and one snack bar.
Answers
Answer:
one glass of milk = 15 carbs
one bar = 14 carbs
Step-by-step explanation:
let 'm' = one glass of milk
let 'b' = one snack bar
system of equations:
2m + 3b = 72
4m + 2b = 88
I used the elimination method and multiplied the 1st equation by -2
-4m - 6b = -144
+ 4m + 2b = 88
-4b = -56
b = 14
now solve for 'm'
2m + 3(14) = 72
2m + 42 = 72
2m = 30
m = 15
SOMEONE PLEASE HELP!!!!! PLEASE!!!
The graph shows the function f(x) = (2.5)x was horizontally translated left by a value of h to get the function g(x) = (2.5)x–h.
On a coordinate plane, 2 exponential functions are shown. f (x) approaches y = 0 in quadrant 2 and increases into quadrant 1. It goes through (negative 1, 0.5) and crosses the y-axis at (0, 1). g (x) approaches y = 0 in quadrant 2 and increases into quadrant 1. It goes through (negative 2, 1) and crosses the y-axis at (0, 6).
What is the value of h?
–2
0
2
5
I will also add the picture of the whole question
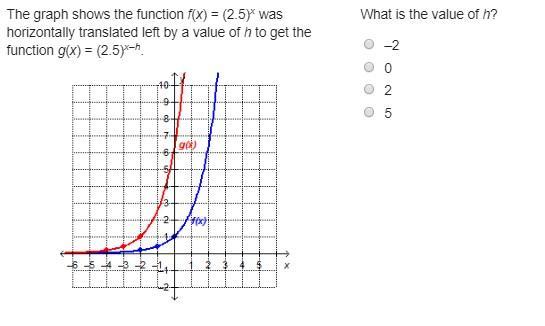
Answers
Answer:
-2
Step-by-step explanation:
Edge2021
Using translation concepts, it is found that the value of h is 5. so option D is correct.
What is a translation?A translation can be represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.
When the expression of function is such that it involves the input to be present as exponent of some constant, then such function is called exponential function.
In this problem, function f(x) is defined by:
\(f(x) = (2.5)^x\)
Function g(x) is defined by
\(g(x) = (2.5)^x-h\)
OR
\(g(x) = (2.5)^x + g\)
Since f(x) the y-axis at (0,1), while g(x) crosses it at (0,6), which means that g(x) is f(x) added to 5, hence h = 5.
Using translation concepts, it is found that the value of h is 5. so option D is correct.
You can learn more about translation concepts at brainly.com/question/21197885
#SPJ2
2 3/4 of 500grams in step by step calculator
Answers
Answer:
To calculate 2 3/4 of 500 grams, follow these steps:
1. Convert the mixed number to an improper fraction:
2 3/4 = (2 x 4 + 3)/4 = 11/4
2. Multiply the improper fraction by 500:
11/4 x 500 = (11 x 500)/4 = 2,750/4
3. Simplify the fraction by dividing the numerator and denominator by their greatest common factor, which is 2:
2,750/4 = (2 x 1,375)/(2 x 2) = 1,375/2
Therefore, 2 3/4 of 500 grams is equal to 1,375/2 grams or 687.5 grams.
Step-by-step explanation:
A high school is voting on a new mascot. Lion Eagle Bee Ninth Grade 45% 32% 23% Tenth Grade 36% 40% 24% Eleventh Grade 50% 28% 22% Twelfth Grade 40% 25% 35% Match the two-way table to the segmented bar graph.
Answers
The steps to create a bar graph are explained below.
To match the two-way table to the segmented bar graph, we need to create a segmented bar graph that represents the data in the table. The table shows the percentage of students in each grade who voted for each mascot option.
Here is how we can match the two-way table to the segmented bar graph:
For the Lion mascot option, the segmented bar graph would have the largest segment for 11th grade, followed by 9th grade, 10th grade, and 12th grade.For the Eagle mascot option, the segmented bar graph would have the largest segment for 10th grade, followed by 11th grade, 9th grade, and 12th grade.For the Bee mascot option, the segmented bar graph would have the largest segment for 12th grade, followed by 9th grade, 10th grade, and 11th grade.By creating a segmented bar graph that represents the data in the two-way table, we can visually compare the percentage of students who voted for each mascot option across different grade levels.
Learn more about graphs here:
https://brainly.com/question/17267403
#SPJ1
Hi question is in photo please help! I’ll give brainly :)

Answers
Answer:
44 in^2
Step-by-step explanation:
Area of rectangle = 5 x 10 = 50 in^2
High of trapezoid = 10 - 6 = 4 in
Area of trapezoid = (7+15) x 4 / 2 = 22 x 4 / 2 = 22 x 2 = 44 in^2
A shipping box is 36 inches by 24 inches by 18 inches
how many cubic feet can it hold
Answers
Answer:
To find the volume of the shipping box in cubic feet, we need to convert the dimensions from inches to feet and then calculate the volume.
Given:
Length = 36 inches
Width = 24 inches
Height = 18 inches
Converting the dimensions to feet:
Length = 36 inches / 12 inches/foot = 3 feet
Width = 24 inches / 12 inches/foot = 2 feet
Height = 18 inches / 12 inches/foot = 1.5 feet
Now, we can calculate the volume of the box by multiplying the length, width, and height:
Volume = Length * Width * Height
Volume = 3 feet * 2 feet * 1.5 feet
Volume = 9 cubic feet
Therefore, the shipping box can hold 9 cubic feet.
Step-by-step explanation:
First convert the units because it's asking for the cubic feet but they give us the measurements in inches.
To convert inches to feet we divide the number by 12.
36 ÷ 12 = 3
24 ÷ 12 = 2
18 ÷ 12 = 1.5
Now to find the volume, we multiply it all together.
3 × 2 × 1.5 = 9
It can hold 9 cubic feet.
Hope this helped!
The risk-free rate is 8%, and the expected return on the market is 16%. As an analyst, you are preparing a recommendation report on the following stock:
Stock S
Beta 0.85
Expected dividend next year $1.10
Growth rate (g) 8%
Current Price (p0) $22
Using the SML, would you recommend to buy or sell the stock?
A) Sell, because the required rate is greater than the expected rate.
B) Sell, because the expected rate is greater than the required rate.
C) Buy, because the required rate is greater than the expected rate.
D) Buy, because the expected rate is greater than the required rate.
Answers
Correct Option is,
D) Buy, because the expected rate is greater than the required rate.
Now, Based on the information you've provided,
To calculate the required rate of return, we can use the SML formula as;
Required rate of return = risk-free rate + beta x (expected market return - risk-free rate)
Plugging in the numbers, we get:
Required rate of return = 8% + 0.85 x (16% - 8%)
= 14.6%
Since the expected rate of return for Stock S is,
= dividend yield + growth rate
= (1.1 / 22 + 8%),
= 9.4%
which is higher than the required rate of return of 14.6%,
Here, the stock is undervalued and would be a good buy.
Therefore, the answer is, option D) Buy, because the expected rate is greater than the required rate.
Learn more about the percent visit:
https://brainly.com/question/24877689
#SPJ1
Use the Alternating Series Estimation Theorem to estimate the range of values of x for which the given approximation is accurate to within the stated error. Check your answer graphically. (Round your answers to three decimal places.)
Answers
The range of values of x for which the given approximation is accurate to within the stated error (0.164375 (0.164375)3/3!=9.993513*10(-7))0.000001.
The series ∑∞n=1bnsin(nπLt) is known as the sine series of f(t) and the series a02+∑∞n=1ancos(nπLt) is known as the cosine series of f(t).
The development series of sin(x) near 0 is, according to
Sin(x) = x/1, x/3, and x/5!...............(1) (1)
Using the above estimate, S(x)=x-x3/3! ................(2)
Consequently, the incorrect phrase for the guess is
error=(2)- (1)
= -(x^5/5! - x^7/7! + x^9/9!)
According to the elective series hypothesis, we only want to make sure that the aggregate will be below as much as feasible and that the outright value of the initial term dropped (x5/5!) is not exactly as far as possible.
This declares what
|x^5/5!| < 0.000001
Speaking for x:
x^5=5!*0.000001=0.000120
x=(0.000120)^(1/5)=0.164375
In light of this, the estimation of sin(x) is x-x3/3! has a blatant error for the range [-0.164375,+0.164375] below 0.000001.
Thus,
sin(0.164375)- (0.164375)^3/3!=9.993513*10^(- 7) < 0.000001
Visit: to learn more about sine series, visit brainly.com/question/15518595
#SPJ4

Let z be a standard normal random variable. Use the calculator provided, or this table, to determine the value of c.

Answers
We have
\(P\mleft(Z>c\mright)=1-P\mleft(Z\le c\mright)=0.2676\)\(P\mleft(Z\le c\mright)=1-0.2576=0.7324\)Then we find the value in the table
ANSWER
c= 0.62

Find the probability that a randomly
selected point within the square falls in the
red-shaded circle.
6
18
18
P =

Answers
The probability of landing on the red shaded circle is 6/18
Concept of probabilityProbability simply measures the chances at which an event could occur in a sample or population.
Mathematically, Probability is calculated thus:
P(X) = required outcome/ Total possible outcomesHere ,
Required = red circle = 6Entire circle = 18P(red circle ) = 6/18
Therefore, the probability is 6/18
Learn more on probability:https://brainly.com/question/24756209
#SPJ1
Find the sample standard deviation.
15 42 53 7 9 12 14 28 47
Answers
The answer to your question is s. sqrt (316.9) = 17.8 when you take the square root of that number. As a result, the correct response is 17.8.
This is further explained below.
What is the sample standard deviation?Generally, Because you need to calculate the sample standard deviation to answer the question, use the following formula:
\(s = \sqrt {{ \sum of x - \bar x}{(n - 1} }\)
There are 9 numbers, there, so n - 1 = 8
find the mean
\(\bar x\): 15 + 42 + 53 + . . . + 47 = 227. 227 / 9
x= 25.2
After that, deduct one from each number and then square the output, as seen here:
(15 - 25.2) = 104.0 (42 - 25.2)²
= 282.2 (53 - 25.2)²
= 772.8
After that, total up all of those values. The response to this, using this illustration as an example, is
\(x=\frac{ 2,535.2}{ 8}\)
x= 316.9.
Read more about standard deviation
https://brainly.com/question/13905583
#SPJ1
Solve 2x = 12 for x.
Answers
Answer:
x=6
step by step explanation:
2x=12
2/2x=12/2
x=6
let g be a group and h be a subgroup such that the index is finite. aha-1 prove that is a finite set
Answers
The assertion that there exists a normal subgroup N of G such that N is of finite index in G and [N ⊂ H] is true and can be proved if "G" is a group and "H" is a subgroup of finite index.
Given,
The statement, "G" is a group and "H" is a subgroup of finite index.
We have to prove that there exists a normal subgroup N of G such that N is of finite index in G and [N ⊂ H].
Group: A group is a finite or infinite collection of elements and a binary operation (referred to as the group operation) in discrete mathematics that together meet the four essential qualities of closure, associativity, identity, and inverse.
Subgroup: If a subgroup "H" also satisfies the four essential criteria of closure, associativity, identity element, and inverse, it is a subset of a group, let's say "G" [denoted by (H ≤ G)].
Here,
By left multiplication, the group G affects the collection of left co-sets (G/H).
Hence it induces the permutation representation [ρ:G→Sₙ], where
[n = |G : H|].
(A permutation representation is a group homomorphism, it should be noted.)
Now, let (N = kerρ) be the kernel of the homomorphism (ρ). Then [N◃G].
The quotient group G/N is isomorphic to a subgroup of Sn according to the first isomorphism theorem.
In particular, G/N is a finite group, hence the index [G:N] is finite.
Finally, we show that [N ⊂ H].
For any (x ∈ N) = [ker (ρ)], we have [x(gH) = gH] for any [g ∈ G].
In particular we have (xH = H),
Hence (x ∈ H).
Learn more about groups and subgroups here;
https://brainly.com/question/28384901
#SPJ4
The equation m=3b represents the times in minutes (m) it takes a chef to cook a certain number of bacon cheeseburgers (b) A: 3 B: 6 C:1/3 D: 1
Answers
For the given equation:
m = 3b
The constant of proportionality is 3, so the correct option is A.
How to determine the constant of proportionality?
After a small search on the internet, I've found that this question asks for the constant of proportionality.
Remember that a proportional relation is of the form:
y = k*x
Where k is the constant of proportionality, and x and y are the variables.
Here the relation is:
m = 3*b
Where m and b are the variables, then the remaining coefficient is the constant of proportionality, which is 3.
In this way, we can see that the correct option is A.
Learn more about proportional relationships:
https://brainly.com/question/12242745
#SPJ1
The odds in favor of an event are given. Compute the probability of the event. (Enter the probability as a fraction.)
4 to 7
Answers
The probability of the event for the given odds in favor (4 to 7) is found as 4/11.
How do you calculate the probability?The inquiry provides the unusual parameters shown below: Odd = 4 to 7First, we must translate the odd into a ratio.Thus, we have the depiction shown below: odds of 4 to 7To continue solving, we must represent the ratio as a fraction.
Thus, we have the depiction shown below.
Odds ratio equals 4/7
We use the following equation to translate the aforementioned odd's expression into a probability expression.
This is displayed as
P = (Odds + 1)/(Odds).
Replace the unknown values in the equation above.
The following equation is what we have.
P = (4/7)/(4/7 + 1)
Analyze the amount
This results
P = (4/7)/(11/7)
Put the quotient in product form.
P = (4/7) * (7/11)
Evaluate
P = 4/11
Thus, the probability of event for the given odds in favor (4 to 7) is found as 4/11.
To know more about the probability, here
https://brainly.com/question/13604758
#SPJ1
How far is the bottom of the ladder from the base of the house?

Answers
Which statement is true?
The
graph of y - log, (X-4) is the graph of y - log, (x) translated 4 units down.
• The graph of y - log, (x) -4 is the graph of y - log, (x) translated 4 units left.
O The graph of y - log, (x) +4 is the graph of y - log, (x) translated 4 units up.
O The graph of y - log,(X+4) is the graph of y - log, (x) translated 4 units right.
Answers
The true statement is, The graph of y = log (x) + 4 is the graph of y = log (x) translated 4 units up.
What is Translation of Functions?Translation of functions is defined as the when each point in the original graph is moved by a fixed units in the same direction.
Given function is,
y = log (x)
When the graph is translated 4 units down,
y = log (x) - 4
When the graph is translated 4 units left,
y = log (x + 4)
When the graph is translated 4 units up,
y = log (x) + 4
When the graph is translated 4 units right,
y = log (x - 4)
Hence the true statement is C.
Learn more about Translation here :
https://brainly.com/question/26238840
#SPJ5
The square below represents one whole.
Express the shaded area as a fraction, a decimal, and a percent of the whole.
Fraction:
Decimal:
Percent:
Answers
Answer:
Below.
Step-by-step explanation:
10 rectangles, 2 are shaded in.
Fraction: 1/5
Decimal: 0.2
Percent: 20%
Write a recursive formula for an, the nth term of the sequence 50, -10, 2, ....
a1
an
11
Answers
Answer:do homework
Step-by-step explanation:
Can someone please scallion or show me what I could do to get this answer?

Answers
Answer:
six hundred and five thousand
Step-by-step explanation:
NO LINKS!!!
answer all 3!!!!
easy brainliest!!



Answers
Answer:
Step-by-step explanation:
1) DE = 6/sin63 = 6.7
DF = 6/tan63 = 3.1
m∠E = 180 - 90 - 63 = 27°
2) tan30 = 1/√3 = UV / (27√10)
UV = (27√10) / √3 · (√3/√3) = (27√30) / 3 = 9√30
3) cosV = 3/8
cos⁻¹(3/8) = 68
m∠V = 68°
What is the probability that either event will occur? 17 A 29 B 14 P(A or B)
Answers
The probability that either event A or B will occur is 43/60
Getting probability value :Using the parameters given
n(A) = 29
n(B) = 14
Total number of events = 29+17+14 = 60
The probability of each event :
P(A) = 29/60
P(B) = 14/60
P(A or B ) = P(A) + P(B)
P(A or B ) = 29/60 + 14/60
P(A or B ) = 43/60
Therefore, the probability of A or B is 43/60
Learn more on probability: https://brainly.com/question/24756209
#SPJ1
Will give brainlist if truly correct
2 box plots. The number line goes from 0 to 20. For East Side Middle School Debate Wins, the whiskers range from 5 to 14, and the box ranges from 10 to 12. A line divides the box at 11. For West Side Middle School Debate Wins, the whiskers range from 3 to 14, and the box ranges from 8 to 12. A line divides the box at 9.
Which of these inferences about the two debate teams are true? Check all that apply.
West Side is more consistent at winning.
East Side is more consistent at winning.
East Side typically wins more debates per year than West Side.
West Side typically wins more debates per year than East Side.
These graphs do not contain enough information from which to draw inferences.
Answers
Answer:
The answers are b and c
Step-by-step explanation:
East Side is more consistent at winning.
East Side typically wins more debates per year than West Side.
