which fraction is equvalent to a terminating decimal
Answers
Related Questions
what digit occurs the least frequently in the numbers between 1 and 1 000 (inclusive)
Answers
The digit that occurs the least frequently in the numbers between 1 and 1,000 is 9, which appears only 271 times.
To answer this question, we need to analyze the numbers between 1 and 1,000 and determine which digit occurs the least frequently. We can start by looking at each individual digit (0-9) and counting how many times it appears in each of the numbers in this range.
For example, the digit 0 appears 192 times in this range, while the digit 1 appears 301 times. We can continue this process for all of the digits and find that the digit that occurs the least frequently is 9, which appears only 271 times.
We can also note that this is not surprising since 9 is the largest single-digit number, and thus, it is less likely to appear in numbers between 1 and 1,000. Additionally, we can observe that the digits 0-8 all appear relatively evenly throughout this range, with each digit appearing between 271-305 times.
In conclusion, the digit that occurs the least frequently in the numbers between 1 and 1,000 is 9, which appears only 271 times.
To know more about digit visit :
https://brainly.com/question/31236720
#SPJ11
Triangle ABC is similar to triangle XYZ Which series of transformations correctly maps △ABC to △XYZ?
Answers
The correct series of transformations that maps triangle ABC to triangle XYZ is a dilation followed by a rotation and a translation.
Similar triangles have the same shape but may differ in size. In order to map triangle ABC to triangle XYZ, we need to find a series of transformations that preserve their shape.
First, a dilation is needed to change the size of triangle ABC to match triangle XYZ. Since triangle XYZ is smaller than triangle ABC, we need to reduce the size of triangle ABC. We can do this by applying a dilation centered at the origin with a scale factor of less than 1.
Next, we apply a rotation to align the corresponding sides and angles of the two triangles. The angle of rotation is the same as the angle of rotation that takes one side of triangle ABC to its corresponding side in triangle XYZ.
Finally, we apply a translation to move the image of triangle ABC to match the position of triangle XYZ. The translation should be such that the corresponding vertices of the two triangles are aligned.
In summary, the correct series of transformations to map triangle ABC to triangle XYZ is a dilation, a rotation, and a translation.
To know more about angle click here
brainly.com/question/14569348
#SPJ11
4. Let A € RMXN (m > n) be a full rank matrix with SVD A=UEVT. Compute SVDs of the following matrices in terms of U, V, and E: (a) (A" A)-1 (b) (ATA)-1 AT (c) A(ATA)-1 (d) A(ATA)- AT
Answers
(a) To compute the SVD of the matrix (A^T A)^(-1) in terms of U, V, and E, we first need to compute the SVD of A itself.
(b) To compute the SVD of the matrix (A^T A)^(-1) A^T in terms of U, V, and E, we again use the SVD of A.
(c) To compute the SVD of the matrix A (A^T A)^(-1) in terms of U, V, and E, we use the SVD of A.
(d) To compute the SVD of the matrix A (A^T A)^(-1) - A^T, we use the SVD of A.
(a)Given the SVD of A as A = U E V^T, where U is an m × m orthogonal matrix, V is an n × n orthogonal matrix, and E is an m × n diagonal matrix with positive entries on the diagonal.
To compute the SVD of (A^T A)^(-1), we can start by expressing A^T A in terms of the SVD of A:
A^T A = (U E V^T)^T (U E V^T)
= V E^T U^T U E V^T
= V E^T E V^T
Taking the inverse of (A^T A) is equivalent to taking the inverse of E^T E since V and E^T are orthogonal matrices. Therefore,
(A^T A)^(-1) = (V E^T E V^T)^(-1)
= V (E^T E)^(-1) V^T
Now, we have expressed (A^T A)^(-1) in terms of V and (E^T E)^(-1). However, we need to further compute the SVD of (E^T E)^(-1).
Let E^T E = D be a diagonal matrix with the singular values squared, i.e., D = diag(d_1^2, d_2^2, ..., d_n^2). Then (E^T E)^(-1) is a diagonal matrix with the reciprocals of the singular values squared on the diagonal, i.e., (E^T E)^(-1) = diag(1/d_1^2, 1/d_2^2, ..., 1/d_n^2).
Therefore, the SVD of (A^T A)^(-1) can be expressed as:
(A^T A)^(-1) = V diag(1/d_1^2, 1/d_2^2, ..., 1/d_n^2) V^T
(b)Given the SVD of A as A = U E V^T, where U is an m × m orthogonal matrix, V is an n × n orthogonal matrix, and E is an m × n diagonal matrix with positive entries on the diagonal.
To compute the SVD of (A^T A)^(-1) A^T, we can substitute the SVD of A into the expression:
(A^T A)^(-1) A^T = (V E^T U^T) (U E V^T)^T
= V E^T U^T U E V^T
= V E^T E V^T
Notice that E^T E is an n × n square diagonal matrix, and since U^T U = I (the identity matrix), the product U^T U simplifies to I. Therefore,
(A^T A)^(-1) A^T = V E^T E V^T
This expression gives the SVD of (A^T A)^(-1) A^T in terms of U, V, and E.
(c)Given the SVD of A as A = U E V^T, where U is an m × m orthogonal matrix, V is an n × n orthogonal matrix, and E is an m × n diagonal matrix with positive entries on the diagonal.
To compute the SVD of A (A^T A)^(-1), we can substitute the SVD of A into the expression:
A (A^T A)^(-1) = U E V^T (V E^T E V^T)^(-1)
= U E V^T V (E^T E)^(-1) V^T
= U E I (E^T E)^(-1) V^T
= U E (E^T E)^(-1) V^T
Here, I represents the identity matrix of appropriate dimensions. The product V^T V simplifies to I since V and V^T are orthogonal matrices. Therefore, we have:
A (A^T A)^(-1) = U E (E^T E)^(-1) V^T
This expression gives the SVD of A (A^T A)^(-1) in terms of U, V, and E.
(d)Given the SVD of A as A = U E V^T, where U is an m × m orthogonal matrix, V is an n × n orthogonal matrix, and E is an m × n diagonal matrix with positive entries on the diagonal.
To compute the SVD of A (A^T A)^(-1) - A^T, we can substitute the SVD of A into the expression:
A (A^T A)^(-1) - A^T = U E V^T (V E^T E V^T)^(-1) - U E V^T
= U E V^T V (E^T E)^(-1) V^T - U E V^T
= U E I (E^T E)^(-1) V^T - U E V^T
= U E (E^T E)^(-1) V^T - U E V^T
Again, the product V^T V simplifies to I since V and V^T are orthogonal matrices. Therefore, we have:
A (A^T A)^(-1) - A^T = U E (E^T E)^(-1) V^T - U E V^T
This expression gives the SVD of A (A^T A)^(-1) - A^T in terms of U, V, and E.
To learn more about matrix Click Here: brainly.com/question/29132693
#SPJ11
Drag each expression to an equivalent form.

Answers
The result of the given exponential expression is given as 1/8, 3^2, 1/5 and 5^-2
Properties of exponentsSome of the properties of exponents are expressed as shown below;
1) a^-n = 1/a^n
In order to answer the given questions, we will use the following properties above;
3^-4 = 1/3^4 where a is equivalent to 3 and n is equivalent to 4
Similarly;
1/2^3 = 2^-3 = 1/8
For the expression 1/3^-2
1/3^-2 = 1/(1/3^2)
1/3^-2 = 3^2
For the expression 5^-1
5^-1 = 1/5^1
5^-1 = 1/5
Also for 1/5^2
1/5^2 = 1/25 = 5^-2
Hence the result of the given exponential expression is given as 1/8, 3^2, 1/5 and 5^-2
Learn more on exponent here: https://brainly.com/question/11975096
#SPJ1
I NEED HELP SOMEONE ASAP
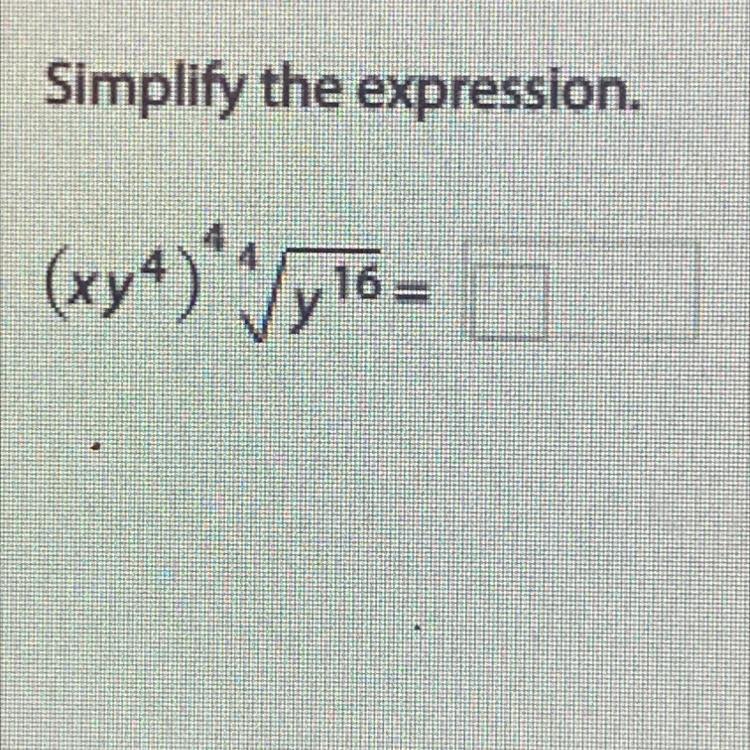
Answers
Answer: x⁴y²⁰
Step-by-step explanation: Distribute the exponent ⁴ over the parentheses
(x y⁴)⁴ becomes x⁴y¹⁶ (multiply exponents)
then take the 4th root of y¹⁶ (divide the exponent of the radicand by the index) ⁴√y¹⁶ becomes y⁴
Then multiply the factors. Add exponents
x⁴y¹⁶ * y⁴ becomes x⁴y²⁰
You have an insurance plan with a \( \$ 1,000 \) deductble and B0\%si20\% co-insurance. How much would you pay if you incured a \( \$ 200,000 \) charge from the cinic? 539,800 \( \$ 40,800 \) \( \$ 19
Answers
If you incurred a $200,000 charge from the clinic and have an insurance plan with a $1,000 deductible and 80%/20% co-insurance, you would pay $40,800.
With a $1,000 deductible, you are responsible for paying the first $1,000 of the medical expenses out of pocket. After meeting the deductible, the co-insurance comes into effect. In this case, the co-insurance is 80%/20%, which means that the insurance company will cover 80% of the remaining expenses, while you are responsible for paying the remaining 20%.
For a $200,000 charge from the clinic, here's how the calculation works:
Amount after deductible: $200,000 - $1,000 = $199,000
Co-insurance: You pay 20% of $199,000 = $39,800
The total amount you would pay is the sum of the deductible and the co-insurance:
$1,000 + $39,800 = $40,800
Therefore, the correct answer is B) $40,800, as this represents the amount you would pay if you incurred a $200,000 charge from the clinic with a $1,000 deductible and 80%/20% co-insurance.
Learn more about insurance here:
https://brainly.com/question/30241822
#SPJ11
The floor of a ballroom has and area of 2,470 square feet. If the length of the floor is 65 feet, what is its width
Answers
Answer:
2,470 = 65 x width
To isolate the width variable, we need to divide both sides of the equation by 65:
2,470 ÷ 65 = width
Simplifying the left side:
38 = width
Therefore, the width of the ballroom floor is 38 feet.
Step-by-step explanation:
To find the width of the ballroom floor, we can use the formula for the area of a rectangle:
Area = length x width
Select the correct answer. the world population in 2013 was about 7.125 billion. in 2003, it was about 6.357 billion. which number represents the increase in the world population between 2003 and 2013?
a. 0.0768 × 107
b. 0.768 × 108
c. 7.68 × 109
d. 7.68 × 108
Answers
Answer:
The number represent the increase in the world population is 0.768 billion.
Step-by-step explanation:
Given : The world population in 2013 was about 7.125 billion. In 2003, it was about 6.357 billion.
To find : Which number represents the increase in the world population between 2003 and 2013?
Solution :
The world population in 2013 was about 7.125 billion.
The world population in 2003 was about 6.357 billion.
The world population between 2003 and 2013 is
The population of 2013- The population of 2003
=7.125\text{ billion}- 6.357\text{ billion}=7.125 billion−6.357 billion
=0.768\text{ billion}=0.768 billion
https://brainly.in/question/22221059
https://brainly.com/question/3226152
a lot is 50m by 38m. A house 30m by 9m is built on the lit. How much area is left over
Answers
Answer:
1480m^2
Step-by-step explanation:
1. Fine the area of the full lot: 35 x 50 = 1750
2. Find the area of the house: 270
3. Subtract the area of the house from the lot: 1750 - 270 = 1480
Your answer is 1480m^2.
Find the missing number to make these fractions equal. 6/? = 4/12
Answers
Step by step explanation
6/? = 4/12
?=6*12/4=18
Multiplying Polynomials
Find each product.
1) 6v(2v + 3) 2) 7(−5v − 8)
3) 2x(−2x − 3)
Answers
A polynomial is an equation made up of coefficients and in determinates that uses only the addition, subtraction, multiplication, and powers of positive-integer variables.
Multiplying Polynomials Find each product. 1) \(6v(2v + 3) 2) 7(-5v - 8)3) 2x(-2x -3)6v(2v + 3)\)
To distribute the 6v over the binomial 2v + 3, we multiply 6v by each term inside the parenthesis:
\(6v(2v) + 6v(3)\)
\(= 12v^2 + 18v7(-5v - 8)\)
To distribute the 7 over the binomial -5v - 8, we multiply 7 by each term inside the parenthesis:
\(7(-5v) + 7(-8)= -35v - 562x(-2x - 3)\)
To distribute the 2x over the binomial -2x - 3, we multiply 2x by each term inside the parenthesis:
\(2x(-2x) + 2x(-3)= -4x^2 - 6x\)
for such more question on Polynomials
https://brainly.com/question/4142886
#SPJ4
one solution for y=2x-1
Answers
One solution for the given linear equation is the poiont (1, 1)
How to find one solution for the linear equation?We want to find a solution for the linear equation:
y = 2x - 1
A solution will be any pair (x, y), such that when we replace these values in the equation, it becomes true.
To find a solution we can evaluate the equation in some value of x, for example, if x = 1
y = 2*1 - 1
y = 2 - 1
y = 1
(1, 1) is a solution for the line.
LEarn more about linear equations at:
https://brainly.com/question/1884491
#SPJ1
How do i find Y and X on triangles ?

Answers
Answer:
X= 5cm
Y=15cm
Step-by-step explanation:
Using by Pythagoras theorem .
The following relation hold for the dimensions of the triangle;
(Hypotenuse)²=(height)²+(base)²
=> H²=h²+b²
On first triangle the unknown X is the hypotenuse, therefore
X² = 3²+4²
=9+16
x² =25
X=√25
X=5cm
On the second triangle, the unknown Y is the height which is given by ;
h²=H²-b²
=>. Y²= 25²-20²
625-400
Y= √225
=15cm
someone please tell me how to work out this type of problem i completely forgot

Answers
Answer:
Plug the x-values into the equation to get the y values. This will give you coordinates that you can graph a line with.
Step-by-step explanation:
For x = -5: y = -3 - 2 * (-5) = 7, so the coordinates are (-5, 7)
For x = -2: y = -3 - 2 * (-2) = 1, so the coordinates are (-2, 1)
(Etc.)
Then, plot these coordinates and draw a line through them to complete the graph.
-If a= 2 and b = 3, then what does ab^2 equal?
Answers
Answer:
36
because 2x3= 6
6x6 is 36
enter the digit that can replace blank

Answers
Hope this helps ;)
Answer:
The digit you replace that box with is 6.
A cubical block of side 14 cm is surmounted by a hemisphere . what is the greatest radius that the hemisphere can have?
Answers
Answer:
9.9cmStep-by-step explanation:
The hemisphere will have its greatest radius along the diagonal of the cube it was surmounted on. The base of the cubical block will be square in nature. Since a cube has all its sides equal, we can find the length of its diagonal using pythagoras theorem as shown.
\(hyp^{2} = adj^{2} +opp^{2}\)
Note that the diagonal will be the hypotenuse of the square face which is the longest sides.
Given adjacent = 14cm and opposite = 14cm
\(hyp^{2} = 14^{2} +14^{2}\\hyp = \sqrt{196+196} \\hyp = \sqrt{392} \\hyp = 19.8cm\)
The diagonal of the base of the cube is 19.8cm which is equivalent to the greatest diameter of the sphere.
The greatest radius that the hemisphere can have = 19.8/2 = 9.9cm
Drawing diagrams
Circles
Radius rDiameter dRelationship between r and d:\(\displaystyle r = \frac{d}{2}\)
Cubes
Length lWidth wHeight hApplication:Let's draw a figure to supplement a visual image to further understand what we need to find. Please refer to the attached image for reference. Please excuse the poor handwriting/drawing. It is also not to scale.
We know that there is a cubical block w/ side measurements of 14 cm. "Surrmounted" means on top. So a hemisphere (half of a sphere) is on top of our block.
If we take a look at our geometrical shape from the top-down angle, we can see that the top would just look like a circle within a square, as depicted in blue.
Labeling our measurements, we can see that the length, width, and height of our cubical block are equal to 14 cm due to the definition of a cube. This extends to the definition of a square as well, so the length and width of our square are also equal to 14 cm.
With the side of the square equal to 14 cm, we know that this is equal to the circle's diameter. So d = 14 cm. We can solve for the radius of the circle/hemisphere by substituting it into the radius formula:
\(\begin{aligned}r & = \frac{d}{2} \\& = \frac{14 \ \text{cm}}{2} \\& = \boxed{ 7 \ \text{cm}} \\\end{aligned}\)
Answer:∴ the greatest radius that the hemisphere can have is equal to 7 cm. Any r > 7 cm would result in the hemisphere being over the edge of the cube.
___
Learn more about Geometry: https://brainly.com/question/27732359
___
Topic: Geometry
Unit: Composition of Geometrical Shapes

what is Quartz to liter?
Answers
A quartz is equivalent to 0.946352946 liters, which means that one liter is equal to approximately 1.05668821 quarts. Quartz and liter are two units of measurement that are used to measure different quantities.
Quartz is a unit of volume, typically used to measure the volume of liquids or gases, while liter is also a unit of volume, commonly used in the metric system to express the volume of liquids and gases.
This conversion is important when working with measurements in different systems or when converting between different units of volume.
It's worth noting that while quartz is still used in some industries, liters are generally more commonly used in everyday life, especially in countries that have adopted the metric system.
In conclusion, understanding the relationship between quartz and liters can be useful in a variety of settings, from cooking and baking to industrial applications.
Conversion between units of measurement is a common task, and knowing the conversion factor between these two units can save time and prevent errors when making calculations or measurements.
To learn more about conversion click on,
https://brainly.com/question/29548067
#SPJ4
Please help me‼️
Question: select all the equations that can be represented by a straight line when graphed on the coordinate plane

Answers
Answer:
B, D, EStep-by-step explanation:
Straight line equation is in the form of:
ax + by = cLets verify the options:
A- no, simplified, it is 1 + xy = 9xB- yesC- no, because of y²D- yesE- yesF - no, simplified it is a quadratic equation30 is 120% of what number? show ur work
Answers
Answer:
30 is 120% of 25
Step-by-step explanation:
30 = 120% of y
\(\frac{120}{100}\) × y = 30
After multiplying both sides by 100 and dividing both sides by 120, we have
y = 30 × \(\frac{100}{120}\)
y = 25

Below is an incomplete probability model showing the likelihood of selecting a marble from a bag. What is the experimental probability of the purple marble? Show work!
A. 3/5
B. 1/2
C. 3/10
D. 2/15

Answers
The calculated experimental probability of the purple marble is (c) 3/10
What is the experimental probability of the purple marble?Given the following table of values
From the table, we have the following readings:
Red = 1/5
Yellow = 2/15
Yellow = 1/3
Orange = 1/30
The sum of probabilities in a probability distribution must be equal to 1
This means that
Purple = 1 - 1/5 - 2/15 - 1/3 - 1/30
When the fractions are evaluated, we have
Purple = 9/30
Simplify
Purple = 3/10
Hence, the probability is 3/10
Read more about probability at
https://brainly.com/question/251701
#SPJ1
I can’t figure out the answer to this, does anybody know?

Answers
Answer:
Option (2).
Step-by-step explanation:
Let f(x) and g(x) are the two functions with domain A and B.
Then (fg)(x) will be the function with domain A∩B
(fg)(x) = f(x)g(x) Domain : A∩B
In this question two functions are,
c(x) = \(\frac{5}{(x-2)}\) and d(x) = (x + 3)
Domain : (x - 2) > 0 ⇒ x > 2
and (x - 2) < 0 ⇒ x < 2
Or domain of (cd)(x) will be C = (-∞, 2)∪(2, ∞).
Similarly, d(x) = x + 3
Domain : All real numbers
: D = (-∞, ∞)
(cd)(x) = c(x)d(x)
= \(\frac{5}{(x-2)}\times (x+3)\)
Domain of (cd)(x) will be,
Domain : C∩D = (-∞, 2)∪(2, ∞) ∩ (-∞, ∞)
: (-∞, 2) ∩ (2, ∞)
Therefore, domain of (cd)(x) will be all real values except 2.
Option (2) will be the answer.
Help please I’ll mark brainliest

Answers
Answer:
- \(\frac{1}{2}\)
Step-by-step explanation:
One cubic down and 2 cubics to the right
Let \theta be an angle in quadrant III such that sec\theta =-(5)/(3). Find the exact values of cot\theta and sin\theta .
Answers
The exact values of \(cot\theta\) and \(sin\theta\) for an angle \(\theta\) in quadrant III, given that \(sec\theta = -\frac{5}{3}\), are \(cot\theta = \frac{3}{5}\) and \(sin\theta = -\frac{4}{5}\).
To find the values of \(cot\theta\) and \(sin\theta\), we first need to determine the value of \(cos\theta\) using the identity \(sec^2\theta = 1 + tan^2\theta\). Since \(sec\theta = -\frac{5}{3}\), we have \(\left(-\frac{5}{3}\right)^2 = 1 + tan^2\theta\). Simplifying, we find that \(tan^2\theta = \frac{16}{9}\).
Next, we can determine the value of \(tan\theta\) by taking the square root of \(\frac{16}{9}\). Since \(\theta\) is in quadrant III, the value of \(tan\theta\) will be negative. Therefore, \(tan\theta = -\frac{4}{3}\).
Finally, we can find \(cot\theta\) by taking the reciprocal of \(tan\theta\), giving us \(cot\theta = \frac{3}{-4} = -\frac{3}{4}\). And using the Pythagorean identity \(sin^2\theta + cos^2\theta = 1\), we can determine \(sin\theta\) as \(sin\theta = -\frac{4}{5}\).
In conclusion, for an angle \(\theta\) in quadrant III, with \(sec\theta = -\frac{5}{3}\), the exact values are \(cot\theta = \frac{3}{5}\) and \(sin\theta = -\frac{4}{5}\).
Learn more about Pythagorean identity here:
https://brainly.com/question/24220091
#SPJ11
Suppose a batch of steel rods produced at a steel plant have a mean length of 187 millimeters, and a variance of 64.
If 416 rods are sampled at random from the batch, what is the probability that the mean length of the sample rods would differ from the population mean by less than
0.65 millimeters? Round your answer to four decimal places.
Answers
the model helps us visualize the movement of gas atoms. b. the model does not show the interactions between the atoms. c. the model depicts the atoms as two-dimensional objects
Answers
The model you're referring to is a simplified representation of gas atoms, which helps us visualize their movement. In this model, atoms are depicted as two-dimensional objects to make it easier to understand.
The given statement suggests that there is a model used to visualize the movement of gas atoms. However, the model has limitations and does not show the interactions between atoms. It also depicts the atoms as two-dimensional objects. This means that the model is only a representation of the atoms' behavior and movement in a simplified manner, and it is not a completely accurate depiction of their behavior in real life.
Additionally, the fact that the model depicts the atoms as two-dimensional objects mean that it does not fully capture the true complexity of the three-dimensional nature of atoms. However, it's important to note that the model does not show the interactions between the atoms, as its primary purpose is to illustrate their motion.
Learn more about Two-dimensional:
brainly.com/question/27271392
#SPJ11
HELP PLEASE
Use the value of the discriminant to determine the number and type of roots for the equation,
X^2 = 4x - 4
A. 2 real, irrational roots
B. 1 real, rational root
C. 2 complex roots
D. 2 real, rational roots
Answers
We are given –
\(\qquad\) \(\twoheadrightarrow\bf x² = 4x -4\)
\(\qquad\) \(\twoheadrightarrow\bf x² -4x +4 = 0\)
Where, a = 1 ; b = -4 ; c = 4Let's find it's discriminant.
We know –
\(\qquad\) \(\purple{\twoheadrightarrow\bf Discriminant = b² - 4ac}\)
\(\qquad\) \(\twoheadrightarrow\sf Discriminant = (-4)² - 4 \times 1 \times 4\)
\(\qquad\) \(\twoheadrightarrow\sf Discriminant = 16-16\)
\(\qquad\) \(\purple{\twoheadrightarrow\sf Discriminant =0 }\)
If Δ (Discriminant) >0here are two separate real roots.If Δ (Discriminant) =0, there are two identical real roots.If Δ (Discriminant) <0, there are no real roots, but there are two complex roots.As we got –
Δ Discriminant is 0 that means , there are two identical real roots. Henceforth, Option (D) 2 real, rational roots – is correct.calculate the length of AC and round off to one decimal place
answer:
step by step method:

Answers
Answer:
\( \cos(67) = \frac{8}{ac} \\ ac = \frac{8}{ \cos(67) } \\ ac = (20.47443732198)\)
8. Maximize p=x+2y subject to 30x+20y
0.1x+0.4y
0.2x+0.3y
x≥0,y≥0
Answers
Answer:5.97
Step-by-step explanation.
you have to look at the question.
you have to look around the question
The very last step is you have to answer it
simplify for this. 22 + (3x3 - 4x4)
Answers
Answer:15
Step-by-step explanation: 1st multiple what’s in the parenthesis (3*3= 9 & 4*4= 16
Next write it out 22+(9-16)
Then you subtract 9 from 16 since it’s in parenthesis So it’s 22+(-7) and since you are adding a negative and a positive together you will have to subtract and keep the sign of the larger number so the answer is 15 since u needed to subtract but 22 is the larger number making it positive answer