what's distributive property of 5x + 1) + 2(4-x)
Answers
Answer:
3x + 9
Step-by-step explanation:
5x + 1 + 2(4 - x)
Expand
5x + 1 + 8 -2x
5x -2x +1+8
3x+9
Answer:
3x + 13
Step-by-step explanation:
5(x +1) + 2(4-x)
=> 5*x + 5*1 + 2*4 - 2*x
=> 5x + 5 + 8 - 2x
=> 5x - 2x + 5 + 8
=> 3x + 13
Hope you understood!!
Related Questions
Evaluate for 5 a - 2 x a for a = 6
Ill give brainliest pls its an emergency i need it fast :((
Answers
hope that helps :)
2(1/4d)+d=96 answer is possibly 64 is that correct?
Answers
Answer:
64
Step-by-step explanation:
2x(1/4 d)+d=96 (Rewrite the expression)
2x1/4d+d=96 (Reduce the numbers)
1/2d+d=96(Calculate)
3/2d=96 (Multiply both sides)
d=64
Susan read 40 pages of a novel in 80 minutes. How long will it take her to read 210 pages of the novel?
Answers
Answer: It will take Susan 420 minutes to read 210 pages of her novel.
What are the steps to solving this equation
8(4-x)=7x+2
Answers
What the meaning of statement this?


Answers
The proof demonstrates that given a well-ordered set W, an isomorphic ordinal can be found using the function F. The uniqueness of this ordinal is established using the Replacement Axioms. The set F(W) is shown to exist for each x in W, and if the least F(W) exists, it serves as an isomorphism of VV onto -y.
Lemma 2.7: This is a previously stated lemma that is referenced in the proof. Unfortunately, without the specific details of Lemma 2.7, it's difficult to provide further explanation for its role in the proof.
Well-ordered set W: A well-ordered set is a set where every non-empty subset has a least element. In this proof, W is assumed to be a well-ordered set.
Isomorphic ordinal: An ordinal is a mathematical concept that extends the notion of natural numbers to represent order and magnitude. An isomorphic ordinal refers to an ordinal that has a one-to-one correspondence or mapping with another ordinal, preserving their order and magnitude properties.
Function F: The function F is defined to assign an ordinal o to each element x in W. This means that for every x in W, there is a corresponding ordinal o.
Existence and uniqueness: The proof asserts that if there exists an ordinal o that is isomorphic to a specific initial segment of the ordinal VV (the set of all ordinals), then this ordinal o is unique. In other words, there is only one ordinal that can be mapped to the initial segment of VV given by x.
Replacement Axioms: The Replacement Axioms are principles in set theory that allow the construction of new sets based on existing ones. In this case, the Replacement Axioms are used to assert that the set F(W) exists, which is the collection of all ordinals that can be assigned to elements of W.
For each x in W: The proof states that for every x in W, there exists an ordinal o that can be assigned to it. If there is no such ordinal, the proof suggests considering the least x for which such an ordinal does not exist.
The least F(W): The proof introduces the concept of the least element in the set F(W), denoted as the least F(W). If this least element exists, it serves as an isomorphism (a one-to-one mapping) of the set of all ordinals VV onto the ordinal -y.
Overall, the proof outlines the existence and uniqueness of an isomorphic ordinal that can be obtained from a well-ordered set W using the function F, and it relies on the Replacement Axioms and the concept of least element to establish this result.
Learn more about axioms here:
https://brainly.com/question/2857184
#SPJ8
Aimee packs ice cream into an ice cream cone. She then puts a perfect hemisphere of ice cream on top of the cone that has a volume of 4 in.3 The diameter of the ice cream cone is equal to its height. What is the total volume of ice cream in and on top of the cone? Use the relationship between the formulas for the volumes of cones and spheres to help solve this problem. Show your work and explain your reasoning.
(4 points)
Answers
Answer:
8 in³
Step-by-step explanation:
\(\boxed{\begin{minipage}{4 cm}\underline{Volume of a sphere}\\\\$V=\dfrac{4}{3} \pi r^3$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \end{minipage}}\)
Since "hemi" is a prefix meaning one half, the volume of a hemisphere is one half the volume of a sphere:
\(\implies V_{\sf hemisphere}=\dfrac{\frac{4}{3}\pi r^3}{2}\)
\(\implies V_{\sf hemisphere}=\dfrac{2}{3}\pi r^3\)
\(\boxed{\begin{minipage}{4 cm}\underline{Volume of a cone}\\\\$V=\dfrac{1}{3} \pi r^2 h$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $h$ is the height.\\\end{minipage}}\)
Given the diameter of the ice cream cone is equal to its height:
diameter = h = 2rSubstitute h = 2r into the equation for the volume of the cone:
\(\implies V_{\sf cone}=\dfrac{1}{3} \pi r^2 \cdot 2r\)
\(\implies V_{\sf cone}=\dfrac{2}{3} \pi r^3\)
Therefore, we can see that the formula for the volume of ice cream in the cone is the same as the formula for the volume of the hemisphere of ice cream.
This means that the volume of the cone of ice cream is equal to the volume of the hemisphere of ice cream.
Given the volume of the hemisphere is 4 in³, the total volume of the ice cream is 8 in³.
The cash register subtracts $2.00 from a $10 Coffee Cafe gift card for every medium coffee the customer buys. Use the graph to write an equation in slope-intercept form to represent this situation.
Answers
The equation of the line in the slope-intercept form is: y = -2.00 x + 10.
The slope and provided point are both in the equation for the straight line.
The generic point (x, y) must satisfy the equation if we have a non-vertical land in a that passes through any point(x1, y1) has gradient m.
y-y₁ = m(x-x₁)
It is the necessary equation for a line in the form of a point-slope.
That gift card to the Coffee Café has been provided. = $10
Medium coffee = $2.00
customers
The quantity of coffees a consumer can purchase can be represented using a linear equation.
Slope formula
m = (8 - 10)/(1 - 0)
m = -2
Now consider the line's point-slope shape.
y-y₁ = m(x-x₁)
( y - 10) = -2.00 ( x - 0)
y = -2.00 x + 10
The slope: m = - 2.00
The equation of the line: y = -2.00 x + 10
The y-intercept is 10
Learn more about slope-intercept here
https://brainly.com/question/1884491
#SPJ1
How to put -4y-3x=12 in slope intercept form??
Answers
Answer:
hmmmmm i need more details <3
A scientist uses the expression 5/9(f-32) to convert temperatures from degrees F° to degrees c°what temperature °f, of a substance at -25 c
Answers
A scientist uses the expression 5/9(f-32) to convert temperatures from degrees F° to degrees c°what temperature °f, of a substance at -25 c
\(\begin{gathered} \frac{5}{9}(\degree F-32)=\degree C \\ \frac{5}{9}(F-32)=-25 \\ 5\mleft(F-32\mright)=9\mleft(-25\mright) \\ 5F-160=-225 \\ 5F=-225+160 \\ 5F=-65 \\ F=-13 \end{gathered}\)From Kansas City to Denver is twice as far as from Kansas City to St. Louis the two distance together total 900 miles what are the two distance?
Answers
Answer:
KC to StL = 300
KC to Den = 600
Step-by-step explanation:
KC to StL was the base distance, so we'll call that x.
KC to Denver is twice as long, so we'll call that 2x.
If we add the together is is 900 miles total.
x + 2x = 900 Combine like terms
3x = 900 Divide by 3
x = 300
If x is 300, then 2x is 600.
You would like to have $20,000 to use a down payment for a home in five years by making regular, end-of-month deposits into an annuity that pays 6% interest compounded monthly.
How much should you deposit each month?
Round your answer to the nearest cent. Do not include the dollar sign in the answer box below.
Answers
The amount that should be deposited monthly is $286.66.
What is a monthly deposit?The monthly deposit is the periodic payment into an investment account that earns interest at a compound rate.
The monthly deposit can be determined using an online finance calculator.
N (# of periods) = 60 months (5 years x 12)
I/Y (Interest per year) = 6%
PV (Present Value) = $0
FV (Future Value) = $20,000
Results:
Monthly Deposit = $286.66
Sum of all periodic deposits = $17,199.36
Total Interest = $2,800.64
Learn more about periodic deposits at https://brainly.com/question/29003232
#SPJ1
Hey Siri of 90 for college students was taken to determine the musical styles you like those 43 students listen to a 45 to classical and 38 jazz also 70 students listen to rock and jazz 26 to Rockin classical and £.23 to classical and jazz finally 13 students listen to all three musical styles constructive and diagram indeterminate Cardinale for each region is a complete Vin diagram to answer the following questions

Answers
We could draw the following Venn's diagram:
Therefore,
13 students listened only rock music
6 students listened classical and Jazz music,but not rock.
28 students listened classical or jazz music, but not rock.
41 students listened to music in exactly one of the musical styles.
23 students listened to music in exactly two of the musical styles.
17 students did not listen to any of the musical styles.

Which is the correct equation for a line that passes through the points (-2,7) and (2,-5)?
y=3x+5
y=1/3x+3
y= -3x-12
y= -3x+1
Answers
Answer:
y= -3x+1
Step-by-step explanation:
x1= -2 x2=2 y1=7 y2=-5
using the formula
(y-y1)/(x-x1)=(y2-y1)/(x2-x1)
(y-7)/(x-(-2))=(-5-7)/(2-(-2))
(y-7)/(x+2)=(-5-7)/(2+2)
(y-7)/(x+2)=(-12)/4
(y-7)/(x+2)=-3
cross multiply
y-7=-3(x+2)
y-7=-3x-6
y=-3x-6+7
y=-3x+1
A store is selling 5 types of hard candies: cherry, strawberry, orange, lemon and pineapple. How many ways are there to choose: (a) 24 candies? (b) 24 candies with at least a piece of each flavor? (b) 24 candies with at least 2 cherry and at least 2 lemon?
Answers
The solution for question a), b) and c) are as follows. The number of ways to choose 24 candies is 20475. And the number of of ways to choose 24 candies with at least a piece of each flavor is 7700. Similarly, the total number of ways to choose 24 candies with at least 2 cherry and at least 2 lemon is 272.
(a) To choose 24 candies from 5 types of hard candies, we can use the stars and bars method. We need to distribute 24 candies among 5 types, where each type can have 0 or more candies.
We can represent this by 24 stars (*) and 4 bars (|) to separate the candies of different types. The number of ways to arrange these stars and bars is the same as the number of ways to choose 4 positions out of 28 to place the bars. Therefore, the number of ways to choose 24 candies is:
(28 choose 4) = 20475
(b) To choose 24 candies with at least a piece of each flavor, we can first choose 5 candies, one of each flavor, and then choose 19 candies from the remaining candies. The number of ways to choose 19 candies from 20 candies (excluding one candy of each flavor) is:
(19 + 4 - 1) choose (4 - 1) = 22 choose 3 = 1540
Therefore, the total number of ways to choose 24 candies with at least a piece of each flavor is:
5 * 1540 = 7700
(c) To choose 24 candies with at least 2 cherry and at least 2 lemon, we can use the inclusion-exclusion principle. Let A be the event that we choose at least 2 cherry, and let B be the event that we choose at least 2 lemon. Then the number of ways to choose 24 candies with at least 2 cherry and at least 2 lemon is:
P(A union B) = P(A) + P(B) - P(A intersect B)
To calculate P(A), we can choose 2 cherry and then choose 20 candies from the remaining 3 types, which is:
(2 choose 2) * (20 + 3 - 1) choose (3 - 1) = 22 choose 2 = 231
Similarly, P(B) is also 231.
To calculate P(A intersect B), we can choose 2 cherry, 2 lemon, and then choose 18 candies from the remaining 3 types, which is:
(2 choose 2) * (2 choose 2) * (18 + 3 - 1) choose (3 - 1) = 20 choose 2 = 190
Therefore, the total number of ways to choose 24 candies with at least 2 cherry and at least 2 lemon is:
2 * 231 - 190 = 272
Learn more about inclusion-exclusion principle here brainly.com/question/27975057
#SPJ4
When commercial aircraft are inspected, wing cracks are reported as nonexistent, detectable, or critical. The history of a particular fleet indicates that 70% of the planes inspected have no wing cracks, 25% have detectable wing cracks, and 5% have critical wing cracks. Five planes are randomly selected. Find the probability that at least one plane has critical cracks.
Answers
Answer:
0.226
Step-by-step explanation:
Given that:
No wing crack (x) = 70%
Detectable wing crack (y) = 25%
Critical wing crack (z) = 5%
Number of samples (n) = 5
Probability that atleast a plane has critical crack:
1 - p(no critical crack)
Using the multinomial distribution calculator :
P(5,0,0) + p(4,1,0) + p(3,2, 0) + p(2,3,0) + p(1,4,0) + p(0,5,0)
From the calculator :
P(5,0,0) + p(4,1,0) + p(3,2, 0) + p(2,3,0) + p(1,4,0) + p(0,5,0) = 0.7741
1 - 0.7741 = 0.2259
= 0.226
For each triangle, find the values of the variables, please help.
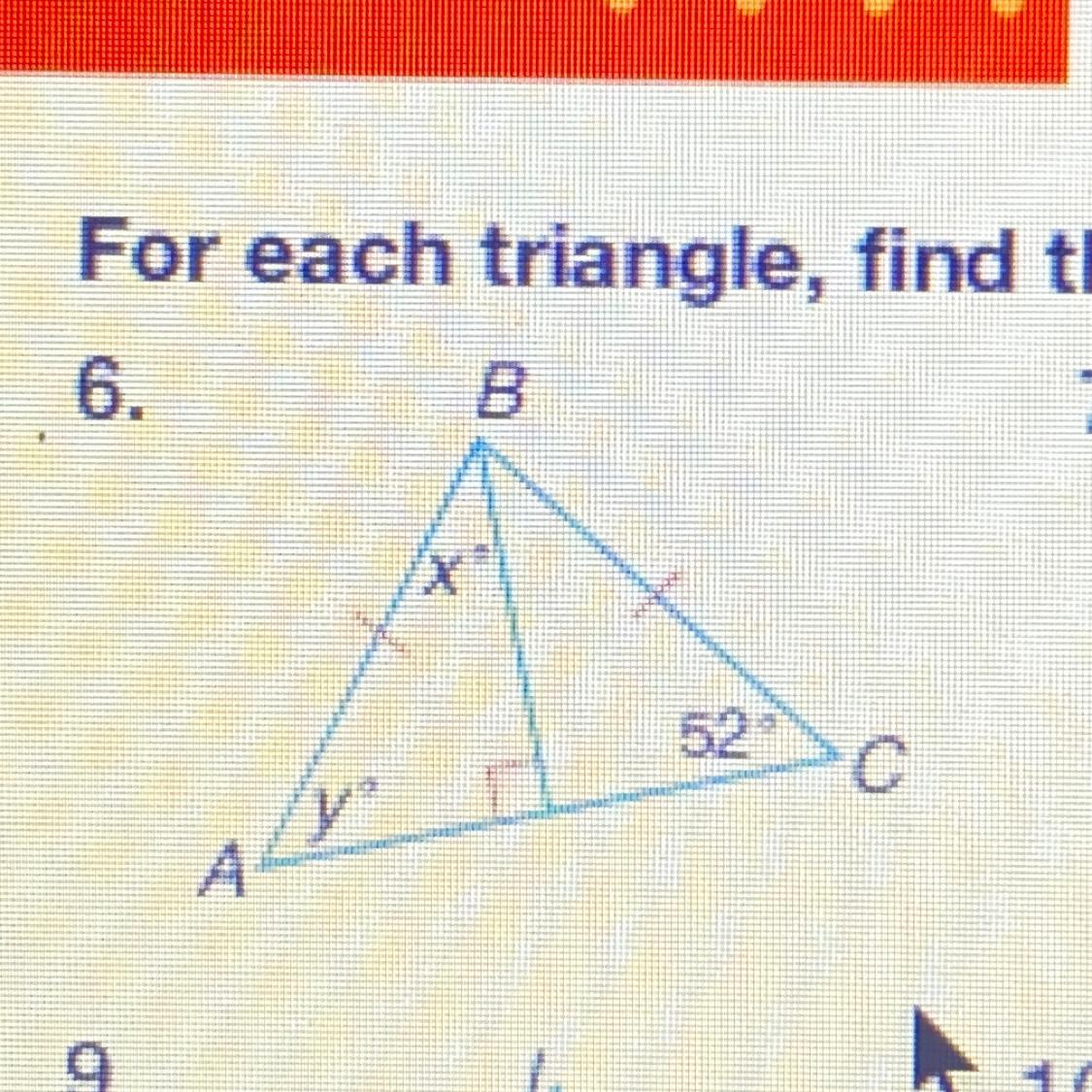
Answers
Answer:
y= 52
x= 38
Step-by-step explanation:
y and 52 equal the same
since a triangle equals 180
the 90 degree angle plus 52 = 142
and 142-180= 38
hope this helps!! <3
Consider all seven-digit numbers that can be created from the digits 0-9 where the first and last digits must be odd and no digit can
repeat. What is the probability of choosing a random number that starts with 5 from this group? Enter a fraction or round your answer to
4 decimal places, if necessary.
Answers
Answer:
1/4 or 0.25
Step-by-step explanation:
The total possibilities of any 7 digit number using 0-9 is :
9×10×10×10×10×10×10=9000000
To work out the total possibilities in this question :
We look at the conditions :
The first digit can only be 5 numbers :
1 , 3 , 5 , 7 , 9
Now we subtract 5 from 9 :
9-5 = 4
Since no repeats for 2 , 3 , 4, 5, 6:
9 , 8 , 7 , 6 , 5,
5 possibilities for the last digit :
Total possibilities for this code :
4 × 9 × 8 × 7 × 6 × 5 × 5 = 302400
If it begins with 5 that is only 1 possibility for the first digit
1 × 9 × 8 × 7 × 6 × 5 × 5 = 75600
Now we make a fraction :
75600÷302400
Dividing top and bottom by 75600 gives you 1/4 or 0.25
Hope this helped and have a good day
Answer:
Step-by-step explanation:
Comment
The first digit and the last digit are both odd. That tells you that so far what you have is one of 5 digits for the first digit and and one of 4 for the last digit. 4 because you can't repeat the first digit.
5, , , , , ,4
2 digits are gone 8 remain.
5* 8 * 7* 6* 5* 4* 4 = 134400
Part 2
Only one number can go at the beginning, and that is a 5. Everything else remains the same.
1 * 8 * 7 * 6 *5 * 4 * 4 = 26880
P(picking a number beginning with a 5 is 25880 /13440) = 0.2
Which expression is equivalent to 8^-3 times 8^-9?
a. 1/8^27
b. 8^-12
c. 8^27
d. 1/8^-12
Answers
Answer:
B
Step-by-step explanation:
Multiplying numbers with exponents rule:
\( {a}^{b} \times {a}^{c} = {a}^{b + c} \)
Explanation of rule: keep the base the same and add the exponents. Keep in mind this rule only works when the base of both numbers are the same.
Applying rule: 8^-3 x 8^-9
keep base as 8 and add the exponents
\( {8}^{ - 3} \times {8}^{ - 9} = {8}^{( - 3) + ( - 9)} = {8}^{ - 12} \)
b is the answer
Find parametric equations and symmetric equations for the line. (Use the parameter t.) The line through (5, 4, 0) and perpendicular to both i j and j k
Answers
Answer:
Step-by-step explanation:
Suppose u = i + j = \(\Big \langle 1,1,0 \Big\rangle\) & v = j + k = \(\Big \langle 0,1,1 \Big\rangle\)
The direction vector for the line u*v is:
\(u\times v = \left |\begin{array}{ccc}i&j&k\\1&1&0\\0&1&1\end {array} \right|\)
= (1-0) i - (1 - 0)j + ( 1- 0) k
= i - j - k
= \(\Big \langle 1,-1,1 \Big\rangle\)
Hence, the equation of the line via the point (5,4,0 ) and the direction vector \(\Big \langle 1,-1,1 \Big\rangle\) is as follows:
r(t) = (5,4,0) + t\(\Big \langle 1,-1,1 \Big\rangle\)
r(t) = (5+t, 4-t, t)
The symmetric equations of the line are:
\(\dfrac{x-5}{1}= \dfrac{y-4}{-1} = \dfrac{z}{1}\)
x - 5 = -(y-4) = z
The parametric equation of the line is:
\(\dfrac{x-5}{1}= \dfrac{y-4}{-1} = \dfrac{z}{1}= t\)
x = 5 + t , y = 4 - t , z = t
Chet has $1200 invested in a bank account modeled by the function P(n) = 1200(1.002)
Answers
Answer:
Answer: 3) R(n) = 1200(1.002)n - 100n
Step-by-step explanation:
After n months, which function represents Chet’s net worth, R(n)?
(1) R(n) = 1200(1.002)n + 100n
(2) R(n) = 1200(1.002)12n + 100n
(3) R(n) = 1200(1.002)n - 100n
(4) R(n) = 1200(1.002)12n - 100n
Answer: 3) R(n) = 1200(1.002)n - 100n
Net worth is the amount of his savings minus his debt,
Everything in the problem is in terms of months, so there is no need to multiply the exponent by 12, which would convert n years into months.
what numbers add up to 6 but multiply to 77
Answers
Answer:
one
Step-by-step explanation:
one is the only number that evenly adds up to six and multplys to 77
A company created a new container in the shape of a
triangular prism that will hold sunflower seeds. A three-
dimensional image of the container is shown below, as
well as a two-dimensional image of the base.
6 in.
3.2 in.
2 in.
3.2 in.
1 in.
square inches
1 in.
The container will be made from cardboard. How many
square inches of cardboard are needed to make one
container? Assume there are no overlapping areas.

Answers
The number of square inches of cardboard that are needed to make one
the container is 18.
We have,
The volume of the triangular prism.
= Area of the triangle x height
Now,
Height = 6 in
And,
To find the area of a triangle, we can use Heron's formula.
A = √(s(s-a)(s-b)(s-c))
where s is the semi-perimeter of the triangle, calculated as:
s = (a + b + c) / 2
In this case, the side lengths of the triangle are 3.2 in, 3.2 in, and 2 in.
Let's calculate the area using Heron's formula:
s = (3.2 + 3.2 + 2) / 2 = 4.2
A = √(4.2(4.2 - 3.2)(4.2 - 3.2)(4.2 - 2))
A = √(4.2 x 1 x 1 x 2.2)
A = √(9.24)
A ≈ 3.04 square inches
Now,
The volume of the triangular prism.
= Area of the triangle x height
= 3.04 x 6
= 18.24 in²
Now,
Area of one cardboard.
= 1² in²
= 1 in²
Now,
The number of square inches of cardboard that are needed to make one
container.
= The volume of the triangular prism / Area of one cardboard
= 18.24 in² / 1 in²
= 18.24
= 18
Therefore,
The number of square inches of cardboard that are needed to make one
the container is 18.
Learn more about Prism here:
https://brainly.com/question/12649592
#SPJ1
A florist currently makes a profit of $20 on each of her celebration bouquets and sells an average of 30 bouquets every week. She noticed that when she reduces the price such that she earns $1 less in profit from each bouquet, she then sells three more bouquets per week. The relationship between her weekly profit, P(x), after x one-dollar decreases is shown in the graph below.
A graph for p of x is a downward open parabola with its vertex at (5, 725) and passes through the points (negative 10, 0), and (20, 0).
Use the graph to complete each statement about this situation.
The maximum profit the florist will earn from selling celebration bouquets is $.
The florist will break-even after one-dollar decreases.
The interval of the number of one-dollar decreases for which the florist makes a profit from celebration bouquets is ( , ).
Answers
Answer:
The maximum profit the florist will earn from selling celebration bouquets is $725.
The florist will break-even after one-dollar decreases when her profit is zero. From the graph, this occurs at x = 10. So the florist will break-even after 10 one-dollar decreases.
The interval of the number of one-dollar decreases for which the florist makes a profit from celebration bouquets is (0, 10). This is because the profit is positive for values of x between 0 and 10, and becomes negative after 10.
Step-by-step explanation:
If the reliability is
r = 0.25,
the equation becomes
R(n) =
0.25n
0.75 + 0.25n
.
What percent improvement is there in the reliability when the test length is doubled?
Answers
The percentage improvement in reliability when test length is doubled is 15%
R(n) = 0.25n / (0.75 + 0.25n)
For a test length of 1substitute n = 1 into the equation :
R(n) = 0.25n / (0.75 + 0.25n)
R(1) = 0.25(1) / (0.75 + 0.25(1))
R(1) = 0.25 / 1
R(1) = 0.25
For a test length of 2when test length is doubled , n = 2
substitute n = 1 into the equation :
R(n) = 0.25n / (0.75 + 0.25n)
R(2) = 0.25(2) / (0.75 + 0.25(2))
R(2) = 0.5 / 1.25
R(2) = 0.4
Percentage improvement can be calculated thus ;
R(2)-R(1)/R(1) × 100%
(0.4-0.25)/0.25 × 100%
0.15 × 100%
=15%
Therefore, percentage improvement in reliability is 15%
Learn more on percentages : https://brainly.com/question/19994681
#SPJ9
A trawler A is 40km west of another trawler B. A set off at 20kmh travel at 25kmh. What course should trawler B take to intercept trawler A
Answers
Trawler B should take a course that is 18 degrees east of north.
How to explain the angleIn order to intercept Trawler A, Trawler B must travel in a direction that will bring it closer to Trawler A. Since Trawler A is traveling due west, Trawler B must travel in a direction that is east of north. The angle that is 18 degrees east of north will bring Trawler B closest to Trawler A.
Here are the steps to find the course that Trawler B should take:
Draw a diagram of the situation.
Label the two trawlers A and B.
Draw a line representing the direction that Trawler A is traveling.
Draw a line representing the direction that Trawler B should travel.
Measure the angle between the two lines.
The angle between the two lines will be 18 degrees. Therefore, Trawler B should take a course that is 18 degrees east of north.
Learn more about angle on
https://brainly.com/question/25716982
#SPJ1
Consider the graph of some function y equals f left parenthesis x right parenthesis.

Answers
The limits of the function for this problem are given as follows:
lim x -> -2 f(x) = 3.lim x -> 1 f(x) does not exist.lim x -> 4 f(x) = -3.How to obtain the limits of the function?In this problem, we are given the graph of the function, hence the limit is given by the value of the function as the function approaches x = a, not the actual numeric value of the function at x = a.
At x = -2, we have that:
To the left of x = -2, the function approaches x = -2 at y = 3.To the right of x = -2, the function approaches x = -2 at y = 3.As the lateral limits are equal, lim x -> -2 f(x) = 3.
At x = 1, we have that:
To the left of x = 1, the function approaches x = 1 at y = 0.To the right of x = 1, the function approaches x = 1 at y = -4.As the lateral limits are different, the lim x -> 1 f(x) does not exist.
At x = 4, we have that:
To the left of x = 4, the function approaches x = 4 at y = -3.To the right of x = 4, the function approaches x = 4 at y = -3.As the lateral limits are equal, lim x -> 4 f(x) = -3.
More can be learned about lateral limits at https://brainly.com/question/26103899
#SPJ1
A quarterback completes 44% of his passes. Show all work.
a. Construct a probability distribution table (out to n = 6) for the number of passes attempted before the quarterback has a completion?
b. What is the probability that the quarterback throws 3 incomplete passes before he has a completion?
c. How many passes can the quarterback expect to throw before he completes a pass?
d. Determine the probability that it takes more than 5 attempts before he completes a pass.
e. If he throws 8 passes on the opening drive, what is the probability that he made at least half of them?
Answers
a.The probability distribution table for the first six attempts is shown below:
X P(X=k)
1 0.44
2 0.56 ×0.44
3 0.56²×0.44
4 0.56³ × 0.44
5 0.56⁴ ×0.44
6 0.56⁵×0.44
b. the probability is 0.1399.
c. the quarterback can expect to throw about 2.27 passes before completing one.
d. the probability is 0.1865.
e. the probability is 0.7349.
what is probability?The possibility or chance of an event occurring is measured by probability. The expression is given as a number between 0 and 1, with 0 denoting impossibility and 1 denoting certainty. Compared to occurrences with a probability closer to 0, those with a probability closer to 1 are more likely to occur.
a. To construct a probability distribution table for the number of passes attempted before the quarterback has a completion, we can use the geometric probability distribution, which is given by:
P(X=k) = \((1-p)^{k-1}\)×p
where X is the number of attempts before the completion, p is the probability of completion on each attempt, and k is the number of attempts.
The probability distribution table for the first six attempts is shown below:
X P(X=k)
1 0.44
2 0.56 ×0.44
3 0.56²×0.44
4 0.56³ × 0.44
5 0.56⁴ ×0.44
6 0.56⁵×0.44
b. The probability that the quarterback throws 3 incomplete passes before he has a completion is given by:
P(X=3) = (1-0.44)³⁻¹× 0.44 × (1-0.44)⁰
= 0.56²×0.44
= 0.1399
Therefore, the probability is 0.1399.
c. The expected number of passes that the quarterback can throw before he completes a pass is given by the formula:
E(X) = 1/p
where p is the probability of completion on each attempt.
In this case, p = 0.44, so the expected number of passes is:
E(X) = 1/0.44
= 2.27
Therefore, the quarterback can expect to throw about 2.27 passes before completing one.
d. The probability that it takes more than 5 attempts before the quarterback completes a pass is given by:
P(X > 5) = 1 - P(X <= 5)
= 1 - [P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5)]
= 1 - [0.44 + (0.56 × 0.44) + (0.56² ×0.44) + (0.56³ × 0.44) + (0.56⁴×0.44)]
= 0.1865
Therefore, the probability is 0.1865.
e. If the quarterback throws 8 passes on the opening drive, the probability that he completes at least half of them is given by the binomial probability distribution, which is given by:
P(X ≥ 4) = 1 - P(X < 4)
where X is the number of completed passes and the probability of completion on each attempt is p = 0.44.
Using the binomial probability distribution table or calculator, we can find:
P(X≥4) = 1 - [P(X=0) + P(X=1) + P(X=2) + P(X=3)]
= 1 - [0.56⁸ + (8× 0.56⁷×0.44) + (28 × 0.56⁶ × 0.44²) + (56× 0.56⁵×0.44³)]
= 0.7349
Therefore, the probability is 0.7349.
To know more about distribution, visit:
https://brainly.com/question/31197941
#SPJ1
Can someone break down how to apply properties of functions please
Answers
Answer:
Linear Function: f(x) = mx + b where m and b are real numbers.
Constant Function: f(x) = b where b is a real number.
Identity Function: f(x) = x.
Square Function: f(x) = x2.
Cube Function: f(x) = x3.
Square Root Function:
Reciprocal Function: f(x) = 1/x.
Absolute Value Function: f(x) = |x|
A can of apple juice contains 175 calories per 2.5 servings at this rate how many calories are in 4 servings
Answers
What is the difference?
-3 2/3 - (-2 1/4)
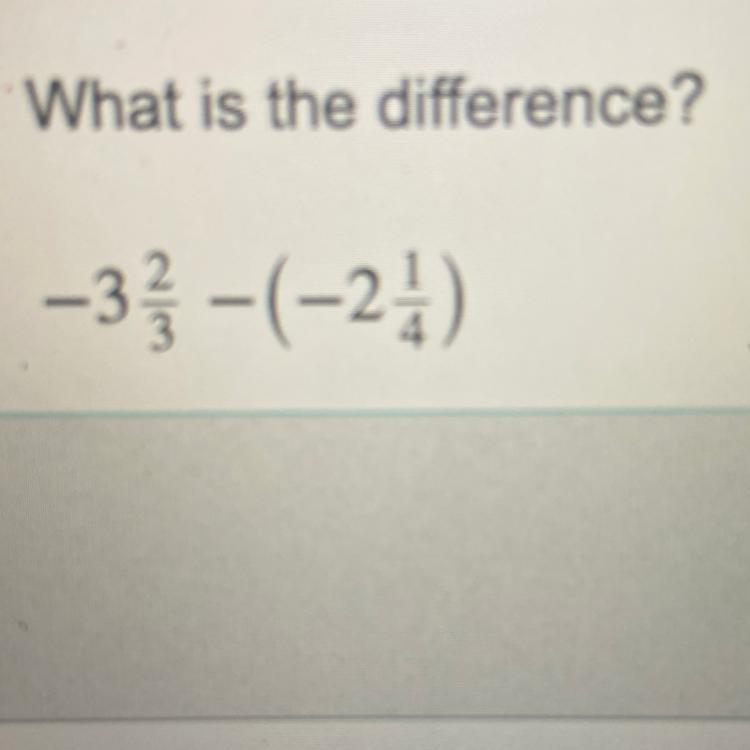
Answers
let's firstly convert the mixed fractions to improper fractions.
\(\stackrel{mixed}{3\frac{2}{3}}\implies \cfrac{3\cdot 3+2}{3}\implies \stackrel{improper}{\cfrac{11}{3}}~\hfill \stackrel{mixed}{2\frac{1}{4}} \implies \cfrac{2\cdot 4+1}{4} \implies \stackrel{improper}{\cfrac{9}{4}} \\\\[-0.35em] ~\dotfill\\\\ -\cfrac{11}{3}-\left( \cfrac{9}{4} \right)\implies -\cfrac{11}{3}+\cfrac{9}{4}\implies \cfrac{-(4)11~~ + ~~(3)9}{\underset{\textit{using this LCD}}{12}} \\\\\\ \cfrac{-44+27}{12}\implies \cfrac{-17}{12}\implies {\Large \begin{array}{llll} -1\frac{5}{12} \end{array}}\)