What is the SUM of 592.3067 and 321.988?
Answers
Answer:
914.2947
Step-by-step explanation:
Related Questions
A sixth grade teacher takes students on a field trip to the beach. One student finds several pebbles that have a rounded shape and are smooth to the touch. What process most likely shaped these pebbles?
The shape of the pebbles is a result of glacial deposition.
The shape of the pebbles is a result of changes in air pressure.
The shape of the pebbles is a result of weathering and deposition.
The shape of the pebbles is a result of being rolled by ocean water.
Answers
Answer:
it's "the shape of the pebbles in a result of being rolled by ocean water"
Find the inverse of the function f(x)=x^3 +4
Answers
Answer:
Step-by-step explanation:
switch the x and f(x) values
x=y^3+4
subtract4
x-4=y^3
cube root
cube root(x-4)=y
Marlon has $600 in his bank account and plans to withdraw $25 each week. Cassandra has $45 in her bank account and plans to deposit $12 each week. Which equation can be used to determine the number of weeks it will take until Marlon and Cassandra have the same balance in their accounts? A)
600−25x=45+12x
cross out
B)
600x−25=45x+12
cross out
C)
25x+12x=600+45
cross out
D)
600x−45x=25+12
Part B
Answers
As per the given situation, it will take 15 weeks for Marlon and Cassandra to have the same balance in their accounts is 600−25x=45+12x. The correct option is A.
We can start by setting up an equation that represents the balance of each person after x weeks.
After x weeks, Marlon's balance would be:
600 - 25x
After x weeks, Cassandra's balance would be:
45 + 12x
To find the number of weeks it will take until they have the same balance, we can set these two expressions equal to each other:
600 - 25x = 45 + 12x
Simplifying this equation, we can combine like terms:
600 = 45 + 37x
Subtracting 45 from both sides:
555 = 37x
Dividing both sides by 37:
x = 15
Therefore, it will take 15 weeks for Marlon and Cassandra to have the same balance in their accounts.
Thus, the correct equation is A) 600−25x=45+12x.
For more details regarding withdraw, visit:
https://brainly.com/question/14289883
#SPJ1
This circle graph shows the favorite colors of kindergarten students at Mountain Sky Elementary School. Seventy-one kindergarten students said blue is their favorite color.
What is the total number of kindergarten students who were surveyed?
Enter your answer in the box.
Answers
Answer:
theirs, is not enough info we need to see the graph this is just not enough info
Step-by-step explanation:
Let {₁, 2, 3, 4, 5, 6} be the standard basis in R. Find the length of the vector € = 3ē₁ + 3e₂ - 5ē3 - 3ē4 + 5ē5 + 4e6. ||x||
Answers
The question asks us to find the length of the vector x = 3e₁ + 3e₂ - 5e₃ - 3e₄ + 5e₅ + 4e₆, where {e₁, e₂, e₃, e₄, e₅, e₆} represents the standard basis in ℝ⁶.
To find the length of the vector x, we need to calculate the Euclidean norm, which is the square root of the sum of the squares of its components.
Given:
X = 3e₁ + 3e₂ - 5e₃ - 3e₄ + 5e₅ + 4e₆
We substitute the coefficients into the Euclidean norm formula:
||x|| = √(3² + 3² + (-5)² + (-3)² + 5² + 4²)
Simplifying the expression:
||x|| = √(9 + 9 + 25 + 9 + 25 + 16)
||x|| = √(93)
Therefore, the length of the vector x is √(93).
Learn more about vector here : brainly.com/question/30958460
#SPJ11
(-4)² = -(4)² True Or False
Help Quick Please!
Answers
Answer: True
Step-by-step explanation: Because Im A Top G
The sale price of a swimming pool after a 18.5% discount is $1189.90. Find the original list price of the pool.
Answers
Answer:
1460
Step-by-step explanation:
18.5% of 1460 = 270.1
1460 - 270.1 = 1189.9
Anyone know how to do this?
Answers
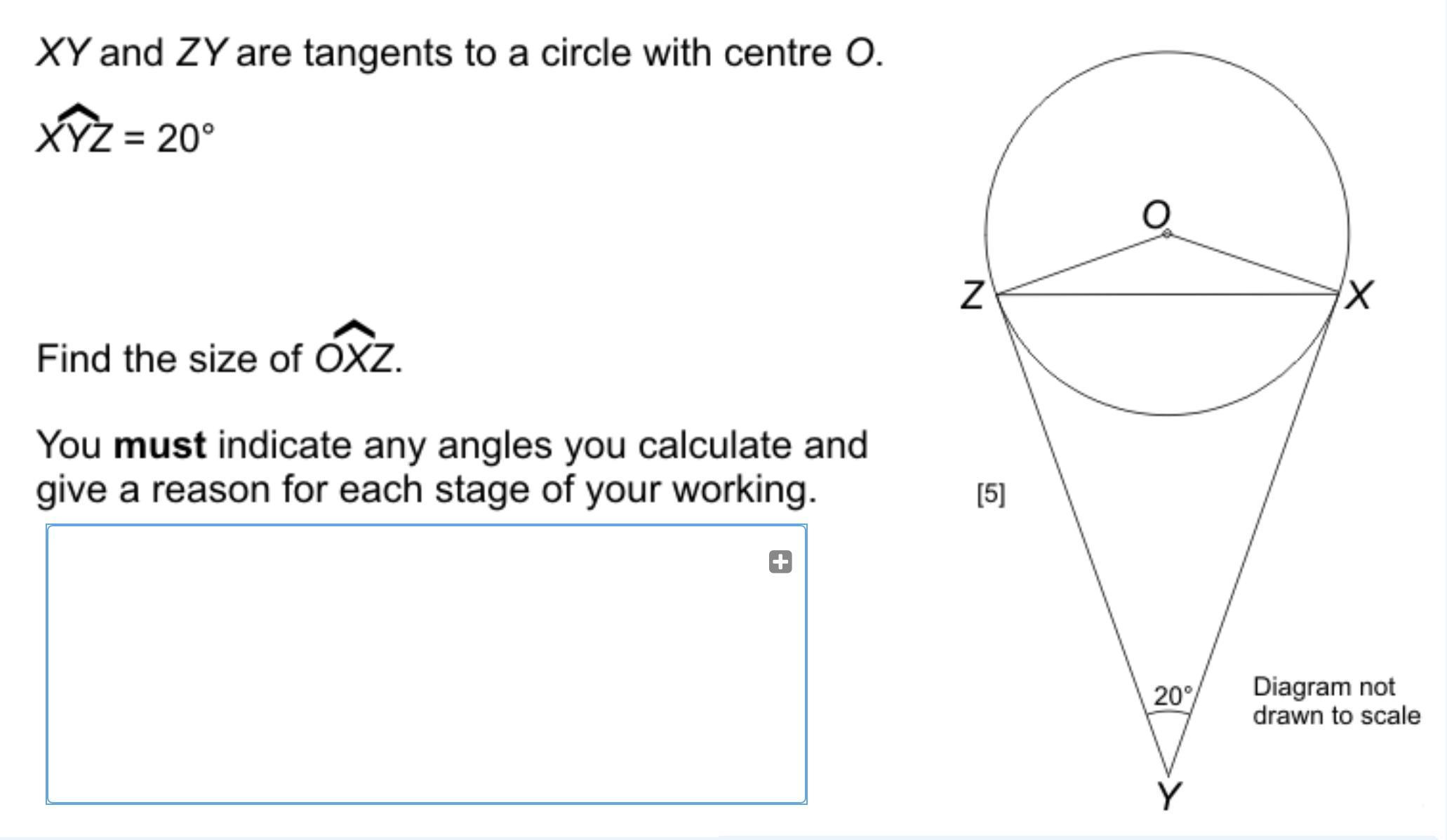
From the given figure, the measure of angle OXZ is 10°.
Given that, XY and ZY are tangents to a circle with center O.
What is the angle formed with tangent and radius?Tangent and radius of a circle meet at 90°. If we draw a radius that meets the circumference at the same point, the angle between the radius and the tangent will always be exactly 90°.
Here, angle formed at the center is
∠ZOX = 180° - ∠XYZ
∠ZOX = 180° - 20°
∠ZOX = 160°
ZO = XO = radius
Now, ΔZOX is an isosceles triangle
So, ∠ZOX +∠OXZ+∠OZX = 180°
⇒ 160° + 2∠OXZ = 180°
⇒ 2∠OXZ = 20°
⇒ ∠OXZ = 10°
Therefore, from the given figure, the measure of angle OXZ is 10°.
To learn more about the tangents to a circle visit:
https://brainly.com/question/23265136.
#SPJ1
Please help ! 13 points

Answers
Answer:
...
Step-by-step explanation:
remeber that for every angle they give you, you need to subtract 90 from it to get the answer.
A die is rolled and a coin is flipped simultaneously. the number rolled on the die and whether the coin lands heads or tails is recorded. how many outcomes are in the sample space? 8 6 10 12
Answers
Answer: 12
Step-by-step explanation:
read the story. zack planted an assortment of tulip bulbs in his garden. half of them were pink tulips. this morning, he noticed that 3 of the tulips had started to sprout. how likely is it that all of them will be pink? zack simulates the situation by flipping a coin 3 times. each time the coin lands on heads, it represents a pink tulip. this table shows the results of 100 trials: number of heads flipped 0 1 2 3 number of trials 12 37 38 11 based on zack's results, what is the probability that all of the tulips will be pink?
Answers
The probability of getting all heads in three-coin tosses is 1/8 or 0.1251. This means that there is a 12.5% chance that all of Zack’s tulips will be pink.
We know that the formula for finding a probability for any outcome is:
Probability = Number of favorable outcomes ÷ Total number of outcomes.
We know that, when a coin is tossed one time then, there are two sample space: {H,T}.
This means that we can get either a head or a tail when a coin is tossed once. Now, since the coin has been tossed 3 times, hence:
The total number of possible outcomes = 2³ =8
This is due to the fact that there are a total of 2ⁿ possible outcomes when a coin is tossed n times.
The eight outcomes would be as follows:
{HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
We are asked to find the probability of getting three heads, or tulips be pink. Therefore,
Probability = 1/8.
Therefore, there are 12.5% chances that all of the Zack's tulips would be pink.
To know more about probability, refer:
https://brainly.com/question/25870256
#SPJ4
Complete question is:
Read the story. Zack planted an assortment of tulip bulbs in his garden. half of them were pink tulips. this morning, he noticed that 3 of the tulips had started to sprout. how likely is it that all of them will be pink? Zack simulates the situation by flipping a coin 3 times. Each time the coin lands on heads, it represents a pink tulip.
This table shows the results of 100 trials:
number of heads flipped 0 1 2 3
number of trials 12 37 38 11
Based on zack's results, what is the probability that all of the tulips will be pink?
Determine a series of transformations that would map Figure O onto Figure P.

Answers
Answer:
OP question dude..
Step-by-step explanation:
Over Powered
why we can evaluate sin x for any x using only the interval [-2, 2].
Answers
There are a few different ways to approach this question, but one possible explanation is based on the fact that the sine function is periodic, meaning it repeats itself over certain intervals.
The sine function has a period of 2π, which means that sin(x + 2π) = sin(x) for any value of x.Now, let's consider the interval [-2, 2] and imagine that we want to evaluate sin(x) for some value of x outside of this interval. Without loss of generality, suppose that x > 2 (similar arguments can be made for x < -2). Then, we can write x as x = 2πn + y, where n is some integer and y is a number in the interval [0, 2π) that represents the "extra" amount beyond the interval of [-2, 2]. (Note that this decomposition is possible because the period of the sine function is 2π.)
Now, we can use the fact that sin(x + 2π) = sin(x) to rewrite sin(x) as sin(2πn + y) = sin(y). Since y is in the interval [0, 2π), we can evaluate sin(y) using any method that works for that interval (e.g., a lookup table, a series expansion, a graph, etc.). In other words, we can always "wrap" any value of x outside of [-2, 2] into the interval [0, 2π) using the periodicity of the sine function, and then evaluate sin(x) for that "wrapped" value.
Now, why did we choose the interval [-2, 2] in particular? One reason is that this interval is convenient for many practical purposes, such as approximating the sine function using polynomial or rational functions (e.g., Taylor series, Chebyshev polynomials, Padé approximants, etc.). These approximations often work best near the origin (i.e., when x is close to 0), and the interval [-2, 2] contains the origin while still being small enough to be computationally tractable.
Another reason is that many real-world applications that involve trigonometric functions (e.g., physics, engineering, statistics, etc.) often involve angles that are small enough to be within the interval [-2, 2] (e.g., angles in degrees or radians that are less than or equal to 180 degrees or π radians). In these cases, evaluating sin(x) within the interval [-2, 2] is often sufficient for practical purposes.
Learn more about polynomial here: brainly.com/question/11536910
#SPJ11
it can be shown that y1=e3x and y2=e−7x are solutions to the differential equation y′′ 4y′−21y=0 on the interval (−[infinity],[infinity]). find the wronskian of y1,y2 (note the order matters)
Answers
The Wronskian of y1 = e^(3x) and y2 = e^(-7x) on the interval (-∞, ∞) is W(y1, y2) = 10.
To find the Wronskian of y1 = e^(3x) and y2 = e^(-7x), we can use the formula for calculating the Wronskian of two functions. Let's denote the Wronskian as W(y1, y2).
The formula for calculating the Wronskian of two functions y1(x) and y2(x) is given by:
W(y1, y2) = y1(x) * y2'(x) - y1'(x) * y2(x)
Let's calculate the derivatives of y1 and y2:
y1(x) = e^(3x)
y1'(x) = 3e^(3x)
y2(x) = e^(-7x)
y2'(x) = -7e^(-7x)
Now, substitute these values into the Wronskian formula:
W(y1, y2) = e^(3x) * (-7e^(-7x)) - (3e^(3x)) * e^(-7x)
= -7e^(3x - 7x) - 3e^(3x - 7x)
= -7e^(-4x) - 3e^(-4x)
= (-7 - 3)e^(-4x)
= -10e^(-4x)
So, the Wronskian of y1 = e^(3x) and y2 = e^(-7x) is W(y1, y2) = -10e^(-4x).
Note that the order of the functions matters in the Wronskian calculation. If we were to reverse the order and calculate W(y2, y1), the result would be the negative of the previous Wronskian:
W(y2, y1) = -W(y1, y2) = 10e^(-4x).
Since the Wronskian is a constant value regardless of the interval (-∞, ∞) in this case, we can evaluate it at any point. For simplicity, let's evaluate it at x = 0:
W(y1, y2) = 10e^(0)
= 10
Therefore, the Wronskian of y1 = e^(3x) and y2 = e^(-7x) on the interval (-∞, ∞) is W(y1, y2) = 10.
Learn more about interval here
https://brainly.com/question/30354015
#SPJ11
what is cme 303 2018
Answers
CME 303 is a course offered at Stanford University that focuses on modeling, simulation, and optimization of complex systems.
It is an introduction to the fundamentals of mathematical optimization, which deals with the problem of finding the best solution to a given problem. The course covers basic optimization theory and algorithms, including linear programming, integer programming, nonlinear programming, dynamic programming, and stochastic programming. Furthermore, it introduces optimization software packages, such as MATLAB, GAMS, and CPLEX, and how to use them for solving real-world optimization problems. It also covers the application of optimization techniques to areas such as finance, engineering, economics, and computer science.CME 303 is a course offered at Stanford University that focuses on modeling, simulation, and optimization of complex systems. The course is taught using lectures, tutorials, and computer lab assignments. In the final project, students apply the techniques learned in the course to solve a real-world problem.
Learn more about complex systems here:
https://brainly.com/question/26671074
#SPJ4
4z−5<−29or4z+3>15
8x+8≥−64and−7−8x≥−79
will mark brainliest
Answers
The solutions for the inequalities are:
z < -6 or z > 3 and -9 ≤ x ≤9
We are asked to solve the inequalities given.
For the inequality 4z−5<−29 or 4z+3>15, we have to solve for z. i.e., find the value for z.
4z−5<−29 or 4z+3>15
⇒ 4z < -29 + 5 or 4z > 15 -3
⇒ 4z < -24 or 4z > 12
⇒ z < -24/4 or z > 12/4
⇒ z < -6 or z > 3
The solution for z are the values above 3 and less than -6.
For 8x+8 ≥ −64 and −7−8x ≥ −79, we need to solve for x.
8x+8 ≥ −64 and −7−8x ≥ −79
⇒ 8x ≥ -64 -8 and -8x ≥ -79 + 7
⇒ 8x ≥ -72 and -8x ≥ -72
⇒ x ≥ -72/8 and -x ≥ -72/8
⇒ x ≥ -9 and x ≤ 9
⇒ -9 ≤ x ≤9
The solution for x are between -9 and 9.
The question is not complete. The complete question is given below:
Solve the system of inequalities.
4z−5<−29 or 4z+3>15
8x+8≥−64 and −7−8x≥−79.
Learn more about solving inequalities at https://brainly.com/question/24372553
#SPJ1
MY NOTES ASK YOUR TEACHER Find the local maximum and minimum values and saddle point(s) of the function. If you have three dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. (Enter NONE In any unused answer blanks.) fx, y)-8-2x+4y-²-4² maximum " (smaller x value) (larger x value) " minimum " (smaller x value) " (larger a value) saddle points Submit Answer ) (smallest x value) ) (largest x value)
Answers
The local maximum and minimum values of the function are as follows: maximum at (smaller x value), minimum at (larger x value), and there are no saddle points.
To find the local maximum and minimum values of the function, we need to analyze its critical points, which occur where the partial derivatives are equal to zero or do not exist.
Let's denote the function as f(x, y) = -8 - 2x + 4y - x^2 - 4y^2. Taking the partial derivatives with respect to x and y, we have:
∂f/∂x = -2 - 2x
∂f/∂y = 4 - 8y
To find critical points, we set both partial derivatives to zero and solve the resulting system of equations. From ∂f/∂x = -2 - 2x = 0, we obtain x = -1. From ∂f/∂y = 4 - 8y = 0, we find y = 1/2.
Substituting these values back into the function, we get f(-1, 1/2) = -9/2. Thus, we have a local minimum at (x, y) = (-1, 1/2).
There are no other critical points, which means there are no local maximums or saddle points. Therefore, the function has a local minimum at (x, y) = (-1, 1/2) but does not have any local maximums or saddle points.
Learn more about function here:
https://brainly.com/question/18958913
#SPJ11
M is between L and N. If LN = 91 and LM = 23, find MN.
Answers
Answer:
MN = 68
Step-by-step explanation:
LN = 91
LM = 23
Points L, M, and N are collinear, therefore, according to the segment addition postulate, the following can be deduced:
LM + MN = LN
23 + MN = 91 (Substitution)
Subtract 23 from both sides
23 + MN - 23 = 91 - 23
MN = 68
evaluate tan(sin^-1)(7/9)
Answers
SOLUTION
Given the question, the following are the steps to solve the problem
Step 1: Write out the question
\(\tan (\sin ^{-1})(\frac{7}{9})\)Step 2: Solve the expression in the first bracket
\(\begin{gathered} \tan (\sin ^{-1})(\frac{7}{9}) \\ (\sin ^{-1})(\frac{7}{9})=51.05755873 \end{gathered}\)Step 3: Calculate the tangent of the result in step 2
\(\begin{gathered} \tan (\sin ^{-1})(\frac{7}{9}) \\ =\tan (51.05755873) \\ =1.237436867 \\ \approx1.2374 \end{gathered}\)Hence, the result from the evaluation of tan(sin^-1)(7/9) is approximately 1.2374
An isosceles triangle has an angle that measures 94º. Which other angles could be in that
isosceles triangle? Choose all that apply.
43°
8°
81°
59°
Answers
Answer:
43°
Step-by-step explanation:
In a isosceles triangle, two angles HAVE to be equal.
This means that 94 can be one of the angles that are equal, or the angle that is not equal to another angle.
Let's start with the fact that 94 can be one of the angles that are equal. (Note: angles in a triangle add up to 180)
94+94+x=180
188+x=180
There is NOT a possible value for x in this situation, as you cannot have a negative value of an angle. Therefore we must try the other situation where 94 is the angle that is not equal to another angle.
x+x+94=180
2x+94=180
Subtract 94 from both sides
2x=86
Divide both sides by 2
x=43
Therefore the answer is 43°
Find the solution of the following initial value problem. y ′′ + y = δ(t − 2π) cost; y(0) = 0, y′ (0) = 1
Answers
The solution of the given initial value problem is y(t) = sin(t) + H(t-2π)cos(t-2π), where H(t) is the Heaviside step function.
To solve the initial value problem, we start by finding the complementary solution, which satisfies the homogeneous differential equation y'' + y = 0. The complementary solution is given by y_c(t) = A sin(t) + B cos(t), where A and B are constants to be determined.
Next, we find the particular solution for the given non-homogeneous term δ(t-2π)cos(t). Since the forcing term is a Dirac delta function at t = 2π, we can write the particular solution as y_p(t) = K(t-2π)cos(t-2π), where K is a constant to be determined.
Applying the initial conditions y(0) = 0 and y'(0) = 1, we can solve for the constants A, B, and K. Plugging in these initial conditions into the general solution, we find A = 0, B = 1, and K = 1.
Therefore, the solution of the initial value problem is y(t) = sin(t) + H(t-2π)cos(t-2π), where H(t) is the Heaviside step function.
The initial value problem with the given conditions is solved by finding the complementary solution and the particular solution. The solution is y(t) = sin(t) + H(t-2π)cos(t-2π), where H(t) is the Heaviside step function. This solution satisfies the given initial conditions y(0) = 0 and y'(0) = 1.
To know more about Heaviside step function follow the link:
https://brainly.com/question/7137484
#SPJ11
Given that the student chosen was a female, find the probability that the student chose invisibility as their superpower. P\left( \text{invisibility }| \text{ female} \right)=P(invisibility ∣ female
Answers
Answer:
\(P(Invisibility | Female) = \frac{2}{3}\)
Step-by-step explanation:
Given
See attachment for two-way table
Required
Determine \(P(Invisibility | Female)\)
This is calculated using the following formula for conditional probability:
\(P(Invisibility | Female) = \frac{n(Invisibility \& Female)}{n(Female)}\)
From the attached table
\(n(Invisibility \& Female) = 32\)
\(n(Female) = 48\)
So, the equation becomes:
\(P(Invisibility | Female) = \frac{32}{48}\)
Simplify
\(P(Invisibility | Female) = \frac{32/16}{48/16}\)
\(P(Invisibility | Female) = \frac{2}{3}\)

Solve the following and explain:
2/3(9x-3)=5x+4-x
Answers
Answer:
3x(3x+2)
Step-by-step explanation:
1. Simplify: (4x2 - 2x) - (-5x2 - 8x).
Solution:
(4x2 - 2x) - (-5x2 - 8x)
= 4x2 - 2x + 5x2 + 8x.
= 4x2 + 5x2 - 2x + 8x.
= 9x2 + 6x.
= 3x(3x + 2).
Answer: 3x(3x + 2)
\(2v^{2} +14=104\)
Answers
Step-by-step explanation:
\(2 {v}^{2} + 14 = 104 \\ 2 {v}^{2} = 104 - 14 \\ 2 {v}^{2} = 90 \\ {v}^{2} = 90 \div 2 \\ {v}^{2} = 45 \\ v = \sqrt{45} \)
I will leave the answer in square root form as i am not sure if you need to round your answer or not.
boy can mow a lawn in 90 minutes and his sister can mow the same lawn in 60 minutes. how long will it take for both mowing at the same time to mow the lawn?
Answers
The time taken by both to mow the lawn is 36 minutes.
This is a question of time and work.
It is given that:-
Time taken by boy to mow the loan = 90 minutes.
Time taken by girl to mow the loan = 60 minutes.
We have to find the time taken by both of them together to mow the lawn.
LCM(60,90) = 180
Let the total work to be done to mow the lawn be 180 units.
Hence,
Efficiency of boy = 180/90 = 2 units
Efficiency of girl = 180/60 = 3 units
Total efficiency = 2 + 3 = 5 units.
Hence, time taken by both of them to mow the lawn = 180/5 = 36 minutes.
To learn more about time and work, here:-
https://brainly.com/question/8032605
#SPJ4
solve the equation 4x^3 + 32x^2 + 42x - 16 = 0, given that one root is equal to the sum of the other two roots
Answers
The solutions to the equation are x = -1, x = -8, and x = 1/2.
How to calculate the valueThe equation 4x³ + 32x² + 42x - 16 = 0 can be divided throuh by 2 as follows:
2x³ + 16x² + 21x - 8 = 0
We can test each of these possible roots by substituting them into the equation and seeing if we get 0. When we substitute -1, we get 0, so -1 is a root of the equation. We can then factor out (x + 1) from the equation to get:
(x + 1)(2x² + 15x - 8) = 0
We can then factor the quadratic 2x² + 15x - 8 by grouping to get:
(x + 8)(2x - 1) = 0
This gives us two more roots, x = -8 and x = 1/2.
Therefore, the solutions to the equation are x = -1, x = -8, and x = 1/2.
Learn more about equations on
https://brainly.com/question/2972832
#SPJ1
HELPPPPPPP PLEASEEEEEEEEEE
Algebra

Answers
Answer:
(-1, -5)
Equation form:
x=-1, y=-5
Step-by-step explanation:
Basically, all you have to do is solve for the first variable in one of the equations, then substitute the result into the other one. It's as simple as that.
Hope this helps
Under his cell phone plan, Joseph pays a flat cost of $48 per month and $3 per gigabyte, or part of a gigabyte. (For example, if he used 2.3 gigabytes, he would have to pay for 3 whole gigabytes.) He wants to keep his bill under $55 per month. What is the maximum whole number of gigabytes of data he can use while staying within his budget?
Answer:
gigabytes
gigabytes
Answers
Answer: 2 is the maximum number of gigabytes
Step-by-step explanation:
Which of the following is the graph of a function of x?
Hurry pls, I need help

Answers
Answer:
A
Step-by-step explanation:
I'm not fully sure :(
The length of a rectangle is 5 meters less than its width. The perimeter is 78 meters. Find the dimensions of the rectangle
Answers
Answer:
above is the solution to the question
