Answers
\(\huge \rm༆ Answer ༄\)
First Consider two points ~ (0 , -3) and (-1 , 0)
Now, use the given formula to calculate slope :
\( \sf \dfrac{y2 - y1}{x2 - x1}\)\( \sf \dfrac{0 - ( - 3)}{ - 1 - 0} \)\( \sf \dfrac{ 0 + 3 }{ - 1}\)\( \sf \dfrac{3}{ - 1} \)\( \sf - 3\)Therefore, the slope of the graph is -3
\( ꧁ \: \large \rm{TeeN \: ForeveR } \: ꧂\)
Related Questions
the gram-schmidt process produces from a linearly independent set {x1, x2, . . . , xp} an orthogonal set {v1, v2, . . . , vp} with the property that span{v1, . . . , vk}
Answers
The statement is true.
An orthogonal set with the same dimension as the initial collection of vectors is created by the Gram-Schmidt process.
Given that,
From a linearly independent collection of {x₁, x₂,..., xp}, the gram-Schmidt process creates an orthogonal set of {v₁, v₂,..., vp} with the feature that for each k, the vectors v₁...vk span the same subspace as that spanned by x₁...xk.
Whether the claim is true or false must be determined.
The statement is true.
An orthogonal set with the same dimension as the initial collection of vectors is created by the Gram-Schmidt process. An orthogonal set is further linearly independent. The orthogonal set produced by the Gram-Schmidt process and the original set will cover the same subspace if their dimensions are the same.
To learn more about orthogonal visit: https://brainly.com/question/2292926
#SPJ4
division ( must show work) 1. t = 10 2. m =12 3. x = 2.5
4 3 5
4. p = 32
2
Answers
Answer:
1. t = 40
2. m = 26
3. x = 12.5
4. p = 64
Step-by-step explanation:
1. t/4 = 10
(4)t/4 = 10(4)
t = 40
2. m/3 = 12
(3)m/3 = 12(3)
m = 36
3. x/5 = 2.5
(5)x/5 = 2.5(5)
x = 12.5
4. p/2 = 32
(2)p/2 = 32(2)
p = 64
If there are 274 million adults in the country, how many believe that divorce is morally wrong?
Answers
The number of adults believes that the divorce is morally wrong is given by 54.8 million.
Given that the total number of adults in the country is = 274 million
Percentage of adults believe that the divorce is morally wrong is given by = 20 %
So the probability of adults believes that the divorce is morally wrong is given by = 20 / 100 = 1 / 5.
The number of adults believes that the divorce is morally wrong is given by
= (Number of total adults) * (Probability of adults believes that the divorce is morally wrong)
= 274 million * (1 / 5)
= 54.8 million
To know more about percentage here
https://brainly.com/question/32197511
#SPJ4
The question is incomplete. The complete question will be -
"If there are 274 million adults in the country, and 20% believe that the action is morally wrong. How many believe that divorce is morally wrong?"
For Which distributions is the median the best measure of center?
Select each correct answer

Answers
Answer: 6, 6, 9 and 25
Step-by-step explanation:
bbringingbbringingout the data's from the graph and arrangementsarrangingarrangingarrangementsarrangingarranging them serially that's from smallest to biggest biggest, then selecting the middle number if the number of entire entries is an odd number but if it's an even number you take the average of the two middle number
Let R={(a,a),(a,b),(a,c),(a,d),(b,a),(b,b),(b,c),(c,c),(d,a),(d,b),(d,d)} be a relation on {a,b,c,d}. Use the matrix method to show that R is not transitive. Note: Must use the matrix method.
Answers
The relation R is transitive, as demonstrated through the matrix method where every pair (x, y) and (y, z) in R implies the presence of (x, z) in R, based on the matrix representation.
To demonstrate this using the matrix method, we construct the matrix representation of the relation R. Let's denote the elements of the set {a, b, c, d} as rows and columns. If an element exists in the relation, we place a 1 in the corresponding cell; otherwise, we put a 0.
The matrix representation of relation R is as follows:
\(\left[\begin{array}{cccc}1&1&1&1\\1&1&1&1\\0&0&1&0\\1&1&1&1\end{array}\right]\)
To check transitivity, we square the matrix R. The resulting matrix, R^2, represents the composition of R with itself.
\(\left[\begin{array}{cccc}4&4&3&4\\4&4&3&4\\2&2&1&2\\4&4&3&4\end{array}\right]\)
We observe that every entry \(R^2\) that corresponds to a non-zero entry in R is also non-zero. This verifies that for every (a, b) and (b, c) in R, the pair (a, c) is also present in R. Hence, the relation R is transitive.
To learn more about Relations, visit:
https://brainly.com/question/29499649
#SPJ11
Find the midpoint of the line segment joining the points (-2,-2) and (-6,9).
Answers
Answer:
\(m=(-4,\frac{7}{2})\) or \((-4,3.5)\)
Step-by-step explanation:
m = midpoint
\(m=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)
\(m=(\frac{-2+(-6)}{2},\frac{-2+9}{2})\)
\(m=(\frac{-8}{2},\frac{7}{2})\)
\(m=(-4,3.5)\)
Consider the system of equations 2x + 5y = 1 3x - 4y = 2 How many solutions does this system have? Explain.
Answers
The system of equations 2x + 5y = 1 and 3x - 4y = 2 has one solution.
How is the system of equations classified?A pair of equations system can be categorized as follows:
The system has no solution if the y-intercepts are varied but the slopes are the same.
The system has a single solution if the slopes are different.
The system has an endless number of solutions if the slopes and y-intercepts match.
The given system of equations are:
2x + 5y = 1
3x - 4y = 2
Write the equations in the standard form:
5y = -2x + 1
4y = 3x - 2
Here, the slope of equation 1 is -2 and the slope of equation 2 is 3.
We know that if the slope is different the system of equations has one solution.
Hence, the system of equations 2x + 5y = 1 and 3x - 4y = 2 has one solution.
Learn more about system of equations here:
https://brainly.com/question/24065247
#SPJ4
which law would you use to simplify the expression (p/q)^3
Answers
Answer:
Step-by-step explanation:

a random sample taken with replacement form the orginal sample and is the same size as the orginal smaple is known as a
Answers
A random sample taken with replacement from the original sample, and having the same size as the original sample, is known as a "bootstrap sample" or "bootstrap replication."
Bootstrapping is a resampling technique used to estimate the sampling distribution of a statistic. When we have a limited sample size and want to draw inferences about the population, we can use bootstrapping to create multiple resamples by randomly selecting observations from the original sample with replacement.
Here's how it works:
We start with an original sample of size n.To create a bootstrap sample, we randomly select n observations from the original sample, allowing for replacement. This means that each observation has an equal chance of being selected and can be selected multiple times or not at all.The selected observations form a bootstrap sample, and we can compute the desired statistic on this sample.We repeat this process a large number of times (usually thousands) to obtain a distribution of the statistic.By examining the distribution of the statistic, we can estimate the sampling variability and construct confidence intervals or perform hypothesis testing.The key idea behind bootstrapping is that the original sample serves as a proxy for the population, and by repeatedly resampling from it, we can approximate the sampling distribution of the statistic of interest. This approach is especially useful when the underlying population distribution is unknown or non-normal.
By using a bootstrap sample that is the same size as the original sample, we maintain the same sample size and capture the variability present in the original data.
Learn more about bootstrapping here:
https://brainly.com/question/30778477
#SPJ11
if a variable x is normally distributed with a mean of 60 and a standard deviation of 15, what is
Answers
For a normally distributed variable x with a mean of 60 and a standard deviation of 15, theprobability P(x < 75) is 0.3173
Here, a variable x is normally distributed a mean of 60 and a standard deviation of 15.
This means, mean (μ) = 60
and the standard deviation (σ) = 15
To find: P(x < 75) .
First we find the z-score.
Using the formula for the z-score,
\(z=\frac{75-60}{15}\)
z = 1
Using standard normal table, the p-value corresponding to z = 1 is:
p = 0.3173
Thus the probability P(x < 75) is 0.3173
Learn more about the probability here:
https://brainly.com/question/29297673
#SPJ4
The complete question is:
if a variable x is normally distributed with a mean of 60 and a standard deviation of 15, what is the probability P(x < 75) .
5(x-y)-5(y+x)
pls help with this
Answers
Answer:
-10y
Step-by-step explanation:
=5x-5y-5y-5x
=5x-5x-5y-5y
=-10y
\(\huge\boxed{\mathrm{\underline{\boxed{Hi\:there, \:hope\:you\:are\:having\:a\:great\:day.}}}}\)5(x-y)-5(y+x)
Let's use the Distributive Property to help us solve.
5(x-y)-5(y+x)
5x-5y-5y-5x
Now, all we have to do is combine like terms.
=>5x-5x-5y-5y
=>-10y
\(\large\boxed{\boxed{Hope\:this\:helps\:you! \:Please\:press\:the\:crown\:button.}}\)
\(\huge\mathrm{\underline{\underline{Please\:comment\:if\:you\:have\:any\:questions.}}}\)
\(\huge\mathfrak{{LoveLastsAllEternity}}\)
The length of the sides of a triangle is given. Determine
whether or not the triangle is right, acute, or obtuse.
6, 8, 10
a
Right
b Acute
a
Obtuse
Answers
Answer:
the triangle is right
Step-by-step explanation:
The Pythagorean theorem dictates that a^2 +b^2=c^2
6^2+8^2=10^2
36+64=100
100=100
what are the common factors of 12 also what are the common of 32:) if u answer thank you so much also i was online for a long time-_-in 6th grade:)))))
Answers
1,2,3,6, and 12 are common factors of 12 and 1,2,4,8,16, and 32 are common factors of 32
Answer:
distinguished
Matrix A has the dimensions 2 x 3 and Matrix B has the dimensions 4 x 6 What are the dimensions of the product AB? X note: if multiplication is not possible put -1 in for both the row column dimensions
Answers
the matrices cannot be multiplied together. the dimensions of the product AB are -1 x -1.
To determine the dimensions of the product AB, we need to ensure that the number of columns in matrix A matches the number of rows in matrix B. If they don't match, the multiplication is not possible, and we'll denote the dimensions as -1.
Matrix A has dimensions 2 x 3, meaning it has 2 rows and 3 columns. Matrix B has dimensions 4 x 6, with 4 rows and 6 columns.
Since the number of columns in matrix A (3) is not equal to the number of rows in matrix B (4), the matrices cannot be multiplied together. Therefore, the dimensions of the product AB are -1 x -1.
To know more about Matrix related question visit:
https://brainly.com/question/29132693
#SPJ11
find the indicated z score. the graph depicts the standard normal distribution with mean 0 and standard deviation 1. .9850
Answers
Therefore, the indicated z-score is 2.45.
To find the indicated z-score, we need to use a standard normal distribution table. From the graph, we can see that the area to the right of the z-score is 0.9850.
Looking at the standard normal distribution table, we find the closest value to 0.9850 in the body of the table is 2.45. This means that the z-score that corresponds to an area of 0.9850 is 2.45.
It's important to note that the standard deviation of the standard normal distribution is always 1. This is because the standard normal distribution is a normalized version of any normal distribution, where we divide the difference between the observed value and the mean by the standard deviation.
To know more about standard deviation visit:
https://brainly.com/question/31516010
#SPJ11
Suppose you have an LFSR with state bits (also known as the seed) (s
5
,s
4
,s
3
,s
2
,s
1
,s
0
)=(0,1,1,1,1,0) and tap bits (also known as feedback coefficients) (p
5
,p
4
,p
3
,p
2
,p
1
,p
0
)=(1,1,0,1,0,0). What are the first 12 bits output by this LFSR? Please enter your answer in the form of unspaced binary digits (e.g. 010101010101). These come in order s
0
s
1
s
2
…s
11
.
Answers
The first 12 bits output by the LFSR are 111011011001.The LFSR is commonly used in various applications such as cryptography, error detection, and sequence generation.
What are the steps and output sequence of an LFSR with the given seed (011110) and tap bits (110100)?The given problem describes a Linear Feedback Shift Register (LFSR) with a specific initial state (seed) and tap bits.
An LFSR is a shift register that generates a sequence of pseudo-random numbers based on its current state and a feedback mechanism.
In this case, the initial state of the LFSR is (011110), and the tap bits are (110100). To generate the output sequence, the LFSR follows these steps:
The initial state is the first output of the LFSR.The LFSR shifts the state to the right, discarding the rightmost bit (s0) and shifting all other bits to the right.The exclusive OR (XOR) operation is performed between the tap bits and certain state bits, specifically: s5 with p5, s4 with p4, s3 with p3, s2 with p2, s1 with p1, and s0 with p0.The result of the XOR operation is assigned as the new leftmost bit (s5) of the shifted state.The LFSR outputs the rightmost bit of the shifted state (the bit that was shifted out in step 2).By repeating these steps, the LFSR generates a sequence of pseudo-random bits.
In this case, we need to determine the first 12 bits of the output sequence.
By applying the steps described above, the first 12 bits of the output sequence are: 111011011001.
Each bit is obtained by performing the XOR operation on the corresponding tap bit and state bit, starting from the initial state and repeating the process for 12 iterations.
It's important to note that the generated sequence is deterministic and will repeat after a certain number of iterations, depending on the length of the LFSR and the arrangement of the tap bits.
Learn more about cryptography
brainly.com/question/88001
#SPJ11
Find the area of the parallelogram.

Answers
Answer: 25 in.
Step-by-step explanation:
A = bh
A = 5 x 5
A = 25
A:bh
A:5x5
A:25
Hope this helps
I NEED HELP WITH MATH PLEASEEE??!

Answers
Answer:
y = -x +2
Step-by-step explanation:
The slope can be found from the slope formula:
m = (y2 -y1)/(x2 -x1)
m = (6 -5)/(-4 -(-3)) = 1/-1 = -1
The y-intercept can be found from ...
b = y -mx
b = 5 -(-1)(-3) = 2
The slope-intercept equation for the line is ...
y = mx +b
y = -x +2 . . . . use the values of m and b we found
Evaluate each expression so the equation is 8b-a and a=4 and b=6
Answers
Answer: 44
Step-by-step explanation: basically replace b with 6 and a with 4 in the expression 8b-a, which turns out to be 8(6)-(4). We're subtracting 4 from the product of 8(6), which is 48. 48-4 = 44
The money spent on gym classes is proportional to the number of gym classes taken. Max spent $\$45. 90$ to take $6$ gym classes. What is the amount of money, in dollars, spent per gym class?
Answers
The amount of money, in dollars, spent per gym class is $\$7.65.
Given that money spent on gym classes is proportional to the number of gym classes taken.
Max spent $45. 90$ to take $6$ gym classes.
To find the amount of money, in dollars, spent per gym class, we need to determine the constant of proportionality.
Let's assume the amount of money spent per gym class as x.
Therefore, the proportionality constant is given by:
Amount spent / number of gym classes taken
= x45.90 / 6 = x
Simplifying the above expression, we get
x = $7.65
Therefore, the amount of money spent per gym class is $\$7.65 per gym class (rounded off to the nearest cent).
Hence, the amount of money, in dollars, spent per gym class is $\$7.65.
To know more about dollars visit:
https://brainly.com/question/15169469
#SPJ11
use properties of operations to write an expression equivalent to -4d+1/2-d
Answers
We can use the properties of operations to rewrite the expression as follows:
-4d + 1/2 - d
First, we can apply the associative property of addition to rearrange the terms:
(-4d + 1/2) - d
Then, we can apply the distributive property to simplify the expression:
-4d + 1/2 - d
= -4d + 1/2 - 1*d
= -4d + 1/2 - d
= (-4 - 1)*d + 1/2
= -5d + 1/2
Therefore, the expression is equivalent to -5d + 1/2.
The associative property of addition states that the grouping of numbers being added does not affect the result. For example, (a + b) + c = a + (b + c).
The distributive property states that the product of a number and a group of numbers is equal to the sum of the products of the number and each individual number in the group. For example, a*(b + c) = ab + ac.
Needing help with question

Answers
Answer:
I think is triangle.........
Assume there is a sample of n
1
=4, with the sample mean
X
1
=35 and a sample standard deviation of S
1
=4, and there is an independent sample of n
2
=5 from another population with a sample mean of
X
ˉ
2
=31 and a sample standard deviation S
2
=5. In performing the pooled-variance t test, how many degrees of freedom are there? There are degrees of freedom. (Simplify your answer.)
Answers
There are 7 degrees of freedom.
In performing the pooled-variance t test, the degrees of freedom can be calculated using the formula:
df = (n1 - 1) + (n2 - 1)
Substituting the given values:
df = (4 - 1) + (5 - 1)
df = 3 + 4
df = 7
Therefore, there are 7 degrees of freedom.
Learn more about degrees of freedom
brainly.com/question/32093315
#SPJ11
There are 7 degrees of freedom for the pooled-variance t-test.
To perform a pooled-variance t-test, we need to calculate the degrees of freedom. The formula for degrees of freedom in a pooled-variance t-test is:
\(\[\text{{df}} = n_1 + n_2 - 2\]\)
where \(\(n_1\)\) and \(\(n_2\)\) are the sample sizes of the two independent samples.
In this case, \(\(n_1 = 4\)\) and \(\(n_2 = 5\)\). Substituting these values into the formula, we get:
\(\[\text{{df}} = 4 + 5 - 2 = 7\]\)
In a pooled-variance t-test, we combine the sample variances from two independent samples to estimate the population variance. The degrees of freedom for this test are calculated using the formula \(df = n1 + n2 - 2\), where \(n_1\)and \(n_2\) are the sample sizes of the two independent samples.
To understand why the formula is \(df = n1 + n2 - 2\), we need to consider the concept of degrees of freedom. Degrees of freedom represent the number of independent pieces of information available to estimate a parameter. In the case of a pooled-variance t-test, we subtract 2 from the total sample sizes because we use two sample means to estimate the population means, thereby reducing the degrees of freedom by 2.
In this specific case, the sample sizes are \(n1 = 4\) and \(n2 = 5\). Plugging these values into the formula gives us \(df = 4 + 5 - 2 = 7\). Hence, there are 7 degrees of freedom for the pooled-variance t-test.
Therefore, there are 7 degrees of freedom for the pooled-variance t-test.
Learn more about t-test
https://brainly.com/question/13800886
#SPJ11
two angles in a triangle measure 2x 30o and 6x - 30o respectively. if these angles are congruent, what is the measure in degrees of the third angle in the triangle?
Answers
the third angle also measures 60 degrees.
If two angles in a triangle are congruent, then they have the same measure. Let's set the measures of the two congruent angles equal to each other and solve for x:
2x + 30 = 6x - 30
Adding 30 to both sides gives:
2x + 60 = 6x
Subtracting 2x from both sides gives:
60 = 4x
Dividing both sides by 4 gives:
x = 15
Now that we have found the value of x, we can use it to find the measures of the two congruent angles:
2x + 30 = 2(15) + 30 = 60
So the two congruent angles each measure 60 degrees.
Finally, we can find the measure of the third angle by using the fact that the sum of the angles in a triangle is always 180 degrees:
180 - 2(60) = 60
To learn more about angle visit:
brainly.com/question/31818999
#SPJ11
Find the surface area.
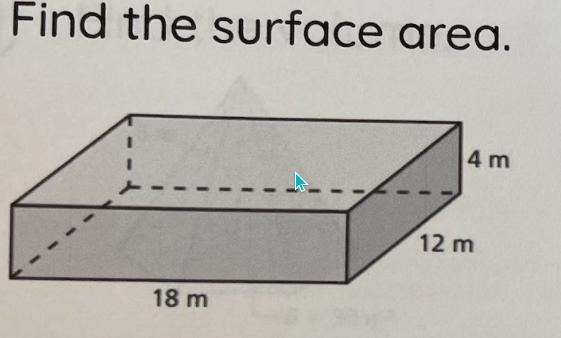
Answers
Answer:
600ft^2
Step-by-step explanation:
Step One: There are two identical faces of each, which means we can multiply each face times two to make it faster. The first face will be 2(4*12)=96. I muliplied by two, because, once again, there are two faces of each.
Step Two: The next is 2(18*12)=432 and lastly, 2(4*18)= 72
Step Three: We just have to add it all up: 72+96+432= 600ft^2
Make a polynomial
-1,-4,2
Answers
Answer:
\(x^3+3x^2-6x-8\)
Step-by-step explanation:
Unfortunately due to your very vague "question", I do not know for sure if -1, -4, and 2 are X values. But assuming they are...
Just like with quadratics, you can foil to easily identify the X value. But this time we are reversing it, and instead of 2 now we have 3.
To set up your polynomial, it should look something like this:
\((x+1)(x+4)(x-2)\)
Now you can FOIL it if it requires you, which I have done for you.
\(x^3+3x^2-6x-8\)
What expression is equivalent to -2x + 7
Answers
Find the specified areas for a Upper N left-parenthesis 0 comma 1 right-parenthesis density. (a) The area below z equals 1.04 Round your answer to three decimal places. areaequals the absolute tolerance is +/-0.001 (b) The area above z equals -1.4 Round your answer to three decimal places. areaequals the absolute tolerance is +/-0.001 (c) The area between z equals 1.1 and z equals 2.1 Round your answer to three decimal places. areaequals the absolute tolerance is +/-0.001
Answers
The area between z=1.1 and z=2.1 is approximately 0.982 - 0.864 = 0.118, rounded to three decimal places.
To find the area below z=1.04 for an Upper N(0,1) density, you will need to use the standard normal distribution table or a calculator with a z-table function. Here are the steps:
1. Locate the value of z=1.04 in the table or use the calculator's function.
2. Find the corresponding area value (which represents the probability or percentage of values below z=1.04).
The area below z=1.04 is approximately 0.851, rounded to three decimal places.
(b) To find the area above z=-1.4 for an Upper N(0,1) density, follow these steps:
1. Locate the value of z=-1.4 in the table or use the calculator's function.
2. Find the corresponding area value.
3. Since we need the area above z=-1.4, subtract the area value found in step 2 from 1.
The area above z=-1.4 is approximately 1 - 0.0808 = 0.919, rounded to three decimal places.
(c) To find the area between z=1.1 and z=2.1 for an Upper N(0,1) density, follow these steps:
1. Locate the values of z=1.1 and z=2.1 in the table or use the calculator's function.
2. Find the corresponding area values for both z=1.1 and z=2.1.
3. Subtract the area value of z=1.1 from the area value of z=2.1 to find the area between them.
The area between z=1.1 and z=2.1 is approximately 0.982 - 0.864 = 0.118, rounded to three decimal places.
Learn more about area
brainly.com/question/27683633
#SPJ11
I need help please! I'm from Spain and I don’t know how to do this!

Answers
Answer:
3.9 ore 39/10
Step-by-step explanation:
3/2+1/2=2
then (2/3-3/5-3)=-44/15+29/6=19/10 that in a desemle woth be1.9
19/10+2=39/10
1.9+2=3.9
Answer:
Step-by-step explanation:I need help please! I'm from Spain and I don’t know how to do this!
Nathan and Audrey have $250 after audrey gave $10 to nathan, they had the same amount of money how much money did nathan have in the beginning
Answers
Answer:
$120
Step-by-step explanation:
250 divided by 2 equals 125.
Audrey= 125+5
So, Audrey has $130.
$250-$130=$120
Hope this helped! :)
