What is the percentage chance of choosing a queen or a king from a standard 52-card deck?
Answers
The probability of choosing a king or queen from a standard 52-card deck is 2/13 or approximately 15.4%.
How can we calculate the percentage?The probability of choosing a king or a queen from a standard 52-card deck can be calculated by first determining the number of kings and queens in the deck. There are four kings (hearts, diamonds, clubs, and spades) and four queens (hearts, diamonds, clubs, and spades) in the deck, for a total of eight cards.
To find the probability of choosing a king or a queen, you need to divide the number of desired outcomes (eight) by the total number of possible outcomes (52).
Probability = Number of desired outcomes / Total number of possible outcomes
Probability = 8 / 52
This simplifies to:
Probability = 2 / 13
Therefore, the probability of choosing a king or a queen from a standard 52-card deck is approximately 0.154 or 15.4%.
Learn more about standard 52-card
brainly.com/question/437884
#SPJ11
Related Questions
at a crosswalk, cars pass on a single lane at times x 0 = 0, x 1 , x 2 , . . ., where {x n : n 0} is a pure renewal process. a pedestrian arriving at time 0 crosses the lane as soon as she sees a time interval ⌧ > 0 between two consecutive cars. how long must she wait, on the average?
Answers
She must wait for E(W) = ∑(n=1 to ∞) [P(T ≤ nX) * (nX - E(T|T ≤ nX))] time on an average.
The pedestrian has to wait on average for a time interval of at least t between two consecutive cars. To find out how long she must wait, we need to calculate the average waiting time.
Let's denote the waiting time as W. We want to find E(W), the expected value of W.
First, let's consider the pedestrian's crossing the lane as a stopping time. A stopping time is a random variable that represents the time at which a certain event occurs.
In this case, the stopping time is the time at which the pedestrian decides to cross the lane, i.e., the time when she sees a time interval of at least t between two consecutive cars.
Let's denote the stopping time as T. We want to find E(T), the expected value of T.
Now, we know that T is a random variable that depends on the arrival times of the cars. The arrival times of the cars form a pure renewal process, denoted as {Rn: n ≥ 0}.
In a pure renewal process, the interarrival times between consecutive events (in this case, the arrival of cars) are independent and identically distributed (i.i.d.) random variables.
Let's denote the interarrival time between the (n-1)th and nth car as Xn. Since the interarrival times are i.i.d., we have Xn = X for all n, where X is the common interarrival time.
Now, let's consider the event T > nX, i.e., the event that the pedestrian has not crossed the lane until the nth car arrives.
The probability of this event is P(T > nX) = P(T > X)^n, where P(T > X) is the probability that the pedestrian has not crossed the lane until one interarrival time has passed.
Since the pedestrian crosses the lane as soon as she sees a time interval of at least t between two consecutive cars, we have P(T > X) = P(no time interval of at least t between two consecutive cars) = P(X < t).
Therefore, P(T > nX) = P(T > X)^n = P(X < t)^n.
Now, let's find P(X < t). Since the interarrival times are i.i.d., we can use the distribution function of X to calculate P(X < t).
Once we have P(X < t), we can find P(T > nX) = P(X < t)^n.
Now, let's consider the event T ≤ nX, i.e., the event that the pedestrian has crossed the lane when the nth car arrives.
The waiting time W in this case is W = nX - T.
To find E(W), we need to find the expected value of W, denoted as E(W).
We can calculate E(W) as follows:
E(W) = ∑(n=1 to ∞) [P(T ≤ nX) * (nX - E(T|T ≤ nX))]
where E(T|T ≤ nX) is the expected value of T conditioned on the event T ≤ nX.
By calculating E(W), we can find the average waiting time for the pedestrian to cross the lane.
Please note that the exact calculations of P(X < t) and E(W) depend on the specific distribution of X, which is not provided in the question. To find the average waiting time, we would need to know the distribution of the interarrival times between the cars.
To know more about time refer here:
https://brainly.com/question/12931977
#SPJ11
What is 1 m equal to in inches?
Answers
One meter is approximately equal to 39.3700787402 inches.
What is Meant by Meter to Inch?The meter to the inch is the conversion of length from the unit meter to inch. The meter and inch are the units which are primarily used to measure the length of any object. The notations used to measure the meter is “m” and inch is “in”. The meter is considered as the International System of Units, whereas inch is used in the imperial and US customary system of measurement.
For example, the conversion of 5 meters into inches is:
5 Meters = 5 x 39.3700787402 inches
5 Meters = 196.8503937008 inches.
Learn more about Meter to inches at:
https://brainly.com/question/15934995
#SPJ4
(3y-1)^5 written in standard form please help!!!!
Answers
Answer:
Step-by-step explanation:
\((3y-1)\)
\((3y-1)*(3y-1)*(3y-1)*(3y-1)*(3y-1)\)
\(243y^5-405y^4+270y^3-90y^2+15y-1\)
3(2x +5) - 2x= 3 (x +6)
Plzzz Someone help me
Answers
Step-by-step explanation:
afsoon the process in the picture hope you understood.

Answer:
x= 3
Step-by-step explanation:
6x + 15 - 2 = 3x + 18
4x +15 = 3x + 18
4x -3x = 18-15
x = 3
% of $30,000,000 = $27,000,000
Answers
Therefore, $27,000,000 is 90 percent of $30,000,000.
What is percent?Percent, denoted by the symbol "%", is a way of expressing a number as a fraction of 100. It is often used to represent ratios, proportions, and rates in everyday life, as well as in business, finance, and other fields. Percentages can also be used to compare values, such as growth rates, inflation rates, or interest rates. For example, if we say that the GDP of a country has increased by 5% over the past year, we mean that the current GDP is 105% of the previous year's GDP, or 1.05 times the previous year's GDP.
Here,
To find out what percent of $30,000,000 is $27,000,000, we can use the following formula:
Percentage = (Part / Whole) x 100%
where "Part" is the amount we want to find the percentage of, "Whole" is the total amount, and the result is expressed as a percentage.
Substituting the given values, we get:
Percentage = ($27,000,000 / $30,000,000) x 100%
Simplifying the fraction by dividing both the numerator and denominator by 1000, we get:
Percentage = (27 / 30) x 100%
Percentage = 0.9 x 100%
Percentage = 90%
To know more about percent,
https://brainly.com/question/29172752
#SPJ1
Complete question:
What percent of 30,00,000 is 27,00,000?
factor the quadratic trinomial x^2-8x+18
(x+ )(x+ )
Answers
Answer:
This is prime.
No factors.
Step-by-step explanation:
use a following question to answer the questions below (the one in the picture)which way does the parabola open besides graphing explain how you can tellfind the focus by handfind the directrix by hand

Answers
We have the parabola:
\((y-2)^2=-24\cdot(x+5)\)The equation above is a parabola in the x-axis, becuase the variable y has the square term.
We can write the equation in the following form:
\(x+5=-\frac{1}{24}(y-2)^2\)Due the term that multiply square y is negative the parabola open to the left.
Now, we can write the general equation of a parabola and find the focus and the directrix:
\(\begin{gathered} \text{Focus = (x,y)=(k,p), Directrix x=b, so the distance to directix is the same to focus:} \\ \sqrt[]{(x-k)^2+(y-p)^2}=x-b \\ (x-k)^2+(y-p)^2=(x-b)^2 \\ x^2-2kx+k^2+(y-p)^2=x^2-2bx+b^2 \\ 2bx-2kx+k^2-b^2=-(y-p)^2 \\ 2(b-k)x+(k+b)(k-b)=-(y-p)^2 \\ 2(b-k)(x-\frac{k+b}{2})=-(y-p)^2 \\ x-\frac{k+b}{2}=-\frac{1}{2(b-k)}(y-p)^2 \end{gathered}\)In our case, we can compare the general formula with the equation and find the values of k,p and b:
\(\begin{gathered} p=2 \\ -\frac{k+b}{2}=5\Rightarrow k+b=-2\cdot5\Rightarrow k=-10-b \\ -\frac{1}{2(b-k)}=-\frac{1}{24}\Rightarrow2(b-(-10-b))=24 \\ b+10+b=\frac{24}{2}\Rightarrow2b+10=12\Rightarrow2b=12-10\Rightarrow b=\frac{2}{2}=1 \\ So,k=-10-1=-11 \end{gathered}\)So, p=2, k=-11 and b=1, and the focus is (k, p) = (-11, 2) and the directrix is x=b=1.
Nhich number line represents the solutions to |x + 4| = 2?
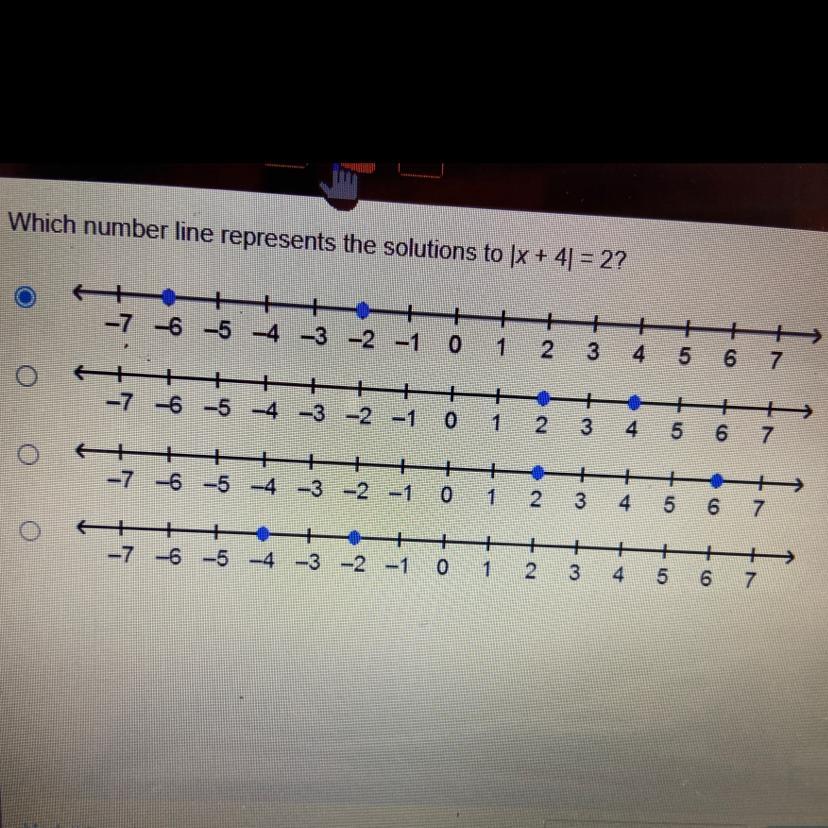
Answers
Answer:
I'm guess that the parentheses looking sign means absolute value so the answer should be the first choice. (-6, and -2)
Step-by-step explanation:
-6 plus 4 = -2 but since we are doing absolute value then the absolute value of -2 is 2.
-2 plus 4 = 2 So, this is also correct because the answer is 2.
Hope this helps! :)
The solution is represented by the first number line, which has the solutions x=-6 and x=-2.
What is number line?A number line is a pictorial representation of numbers on a straight line. In elementary mathematics, a number line is a picture of a graduated straight line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real number to a point.
here, we have,
We have an absolute value function for the equation.
This means that we should have two different solution in the real number line.
As the equation is
|x + 4| = 2
when we clear out the absolute value, we will have two possible solutions:
x + 4 = 2
and
-(x + 4) = 2
now we clear x from both equations
x + 4 = 2 ⇒ x = -2
-(x + 4) = 2 ⇒ x = -6
Then, we have that x=-2 and x=-4 are the solutions for the equation, and therefore the number line that represents the solution is the first one, where the points -6 and -2 are highlighted.
To learn more on number line click:
brainly.com/question/29162579
#SPJ7
The table shows the cost of pizzas. What is the cost of 12 pizzas?

Answers
Answer:
The cost of 12 pizzas is $72.
Step-by-step explanation:
3x6 = 18
6x6= 36
9x6= 54
12x6= 72
so it should be $72.
Answer:
72
Step-by-step explanation:
Apples are prepared in a process with two resources. The first resource has a capacity of 2.1 apples per hour. The capacity of the second resource is 4.4 apples per hour. The first resource has 1 worker and the second resource has 4 workers. Demand for this process is 1.6 apples per hour. Wages are $8 per hour.
What is the cost of direct labor (in $)?per unit
Answers
The cost of direct labor per unit is $5.628 per apple.
To calculate the cost of direct labor per unit, we need to determine the total labor hours required to produce one unit of output and then multiply it by the wage rate.
Let's denote the labor hours required for the first resource as "L₁" and the labor hours required for the second resource as "L₂".
The first resource has a capacity of 2.1 apples per hour, and the demand is 1.6 apples per hour. Therefore, the labor hours required for the first resource per unit of output are:
L₁ = 1 apple / (2.1 apples/hour) = 0.4762 hours/apple (rounded to 4 decimal places)
The second resource has a capacity of 4.4 apples per hour, and the demand is 1.6 apples per hour. Therefore, the labor hours required for the second resource per unit of output are:
L₂ = 1 apple / (4.4 apples/hour) = 0.2273 hours/apple (rounded to 4 decimal places)
Now, let's calculate the total labor hours required per unit:
Total labor hours per unit = L₁ (first resource) + L₂ (second resource)
= 0.4762 hours/apple + 0.2273 hours/apple
= 0.7035 hours/apple (rounded to 4 decimal places)
Finally, to calculate the cost of direct labor per unit, we multiply the total labor hours per unit by the wage rate:
Cost of direct labor per unit = Total labor hours per unit * Wage rate
= 0.7035 hours/apple * $8/hour
= $5.628 per apple (rounded to 3 decimal places)
To know more about direct labor:
https://brainly.com/question/13126873
#SPJ4
a number y is 15 larger than a positive number x. if their sum is not more than 85, what are the possible values of y?
Answers
Answer:
y = x + 15 –(1)
x + y = 85
Putting (1)'s value,
x + x + 15 = 85
2x + 15 = 85
2x = 85 - 15 = 70
x = 70/2 = 35
\(\)
The value of y is 50.
Two simultaneous equations can be formed from the given question:
y - x = 15 equation 1
y + x = 85 equation 2
In order to determine the value of x, subtract equation 1 from 2
2x = 70
Dvidie both sides of the equation by 2
x = 70 / 2
x = 35
Substitute for x in equation 1
y - 35 = 15
y = 35 + 15
y = 50
To learn more about simultaneous equations, please check: https://brainly.com/question/25875552
company xyz know that replacement times for the quartz time pieces it produces are normally distributed with a mean of 12.6 years and a standard deviation of 0.9 years.find the probability that a randomly selected quartz time piece will have a replacement time less than 10 years?
Answers
The probability that a randomly selected quartz time piece from company XYZ will have a replacement time of less than 10 years can be determined using the normal distribution with a mean of 12.6 years and a standard deviation of 0.9 years.
To calculate the probability, we need to find the area under the normal distribution curve to the left of 10 years. First, we need to standardize the value of 10 years using the formula z = (x - μ) / σ, where x is the value (10 years), μ is the mean (12.6 years), and σ is the standard deviation (0.9 years). Substituting the values, we get z = (10 - 12.6) / 0.9 = -2.89.
Next, we look up the corresponding z-score in the standard normal distribution table or use statistical software. The table or software tells us that the area to the left of -2.89 is approximately 0.0019
. This represents the probability that a randomly selected quartz time piece will have a replacement time less than 10 years. Therefore, the probability is approximately 0.0019 or 0.19%.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
The average score of 100 students taking a statistics final was 70 with a standard deviation of 7. Assuming a normal distribution, what is the probability that a student scored greater than 65?
Multiple Choice
0.7611
−0.714
0.2611
0.2389
Answers
the probability that a student scored greater than 65 is 0.2389.
The probability that a student scored greater than 65 can be calculated using the standard normal distribution and the z-score. The z-score represents the number of standard deviations a value is from the mean, and can be calculated as follows:
z = (x - mean) / standard deviation
Where x is the score of interest (65)
Mean is the average score of the students (70)
Standard deviation is the standard deviation of the scores (7).
Plugging in the values, we get
z = (65 - 70) / 7 = -0.714.
Using a standard normal distribution table, we can find the probability that a student scored greater than 65 by finding the area to the right of the z-score. The probability of a student scoring greater than 65 is approximately 0.2389, or 23.89%.
To know more about probablity click here:
https://brainly.com/question/30034780#
#SPJ11
Let F(x) be an antiderivative of (ln x)^3/x. If F(1) = 0, then F(9) =
a. .048
b. .144
c. 5.827
d. 23. 308
e. 1,640.250
Answers
the value of F(9) is approximately 23.308.
To find the value of F(9) given that F(x) is an antiderivative of (ln x)^3/x and F(1) = 0, we can use the fundamental theorem of calculus.
According to the fundamental theorem of calculus, if F(x) is an antiderivative of a function f(x), then:
∫[a,b] f(x) dx = F(b) - F(a)
Since F(1) = 0, we can write:
∫[1,9] (ln x)^3/x dx = F(9) - F(1)
To evaluate the integral, we can make a substitution:
Let u = ln x, then du = (1/x) dx
The integral becomes:
∫[ln 1, ln 9] u^3 du
Integrating u^3 with respect to u:
[(1/4)u^4] | [ln 1, ln 9] = (1/4)(ln 9)^4 - (1/4)(ln 1)^4
Since ln 1 = 0, we have:
(1/4)(ln 9)^4 - (1/4)(ln 1)^4 = (1/4)(ln 9)^4
Therefore, F(9) - F(1) = (1/4)(ln 9)^4
Since F(1) = 0, we can conclude that F(9) = (1/4)(ln 9)^4.
Calculating this value:
F(9) = (1/4)(ln 9)^4 ≈ 23.308
to know more about calculus visit:
brainly.com/question/29097043
#SPJ11
Which point do the graphs of f and g have in common?
f(x) = log2x and
g(x) = log10x.
Answers
The point that the graphs of f and g have in common are (1,0)
How to get the points?The given functions are:
f(x) = log₂x
and
g(x) = log₁₀x
We know that logarithm of 1 is always zero.
This means that irrespective of the base, the y-values of both functions will be equal to 0 at x=1
Therefore the point the graphs of f and g have in common is (1,0).
Learn more about graph on:
https://brainly.com/question/19040584
PLEASE ANSWER THESE! I WILL GIVE BRAINLIEST!! YOU NEED TO Solve each equation. Find the missing number by step by step!

Answers
Step-by-step explanation:
4. E=-6
-9
multiply both sides by the LCM=-9
-9 × (e) = -6×-9
-9
therefore the LCM will cancel I out the denominator
e = -6×-9
e= -54
5. K =2
12
multiply through by the LCM=12
12×(k)=2×12
12
cross out
k=24
6. m=-10
6
multiply through by the LCM=6
6×m=-10×60
6
cross out
m=-60
So follow suit
Porter is visiting India and would like to purchase some local spices. He finds some spices that cost 401.39 rupees. If the current exchange rate is 1 dollar:73.6500 rupees, how much do the spices cost in U.S. dollars?
Answers
Answer:
hey
Step-by-step explanation:
A recipe needs 1/2 cup of water for every 2 cup at of sugar.if toy plan to use 8 cups of sugar,how much water will you need?
Answers
4 cups of water is your answer.
Step-by-step explanation:
Determine all values of h and f for which the system x + 3y = h and -4x + ky = -9 has no solution.
Answers
For any price of h and k = -12, the system x + 3y = h and -4x + ky = -9 will haven't any answer.
To determine the values of h and okay for which the device of equations has no answer, we want to locate the situations underneath which the equations are inconsistent or parallel.
The given system of equations is:
Equation 1: x + 3y = h
Equation 2: -4x + ky = -9
For the gadget to haven't any answer, the lines represented with the aid of these equations should be parallel and in no way intersect. In different phrases, the slopes of the traces need to be equal, but the y-intercepts should be specific.
Let's first discover the slopes of the traces. The slope-intercept form of Equation 1 is y = (-1/3)x + (h/3), wherein the slope is -1/3. The slope-intercept shape of Equation 2 is y = (4/k)x - (9/k), wherein the slope is 4/k.
For the strains to be parallel, the slopes should be equal. Therefore, we have the condition: -1/3 = 4/k.
To locate the values of h and okay for which the gadget has no answer, we need to locate the values of h that satisfy the situation -1/3 = 4/k.
Solving this equation for ok, we've got:
-1/3 = 4/k
-1 = 12/k
k = -12
Substituting k = -12 returned into the equation -1/3 = 4/k, we've:
-1/3 = 4/(-12)
-1/3 = -1/3
Since the equation holds real for any value of h, there aren't any restrictions at the price of h.
Therefore, for any price of h and k = -12, the system x + 3y = h and -4x + ky = -9 will haven't any answer.
To know more about equations,
https://brainly.com/question/29797709
#SPJ4
The system of equations has no solution when k is equal to 12. The value of h can be any real number.
To determine the values of h and f for which the system has no solution, we need to analyze the coefficients of the variables and the constants in the equations.
The given system of equations is:
x + 3y = h
-4x + ky = -9
We can rewrite the second equation as:
-4x + ky = -9
Dividing both sides of the equation by -4, we get:
x - (k/4)y = 9/4
Comparing the coefficients of x and y in the two equations, we can see that the slopes of the lines represented by the equations are different when k is not equal to 12.
Therefore, for the system to have no solution, k must be equal to 12.
As for the value of h, it can be any real number since it does not affect the slopes of the lines.
Learn more:About system of equations here:
https://brainly.com/question/21620502
#SPJ11
14. balls in an urn two balls are selected at random from an urn containing two white balls and three red balls. what is the conditional probability that both balls are white, given that at least one of them is white?
Answers
Given at least one white ball, the conditional probability of two white balls is (1/10) / (7/10) = 1/7.
what is probability?A probability is a number that expresses the possibility or probability that a specific event will take place. Probabilities can be stated as percentages ranging from 0% to 100% or as percentages ranging from 0 to 1.
\(P(WW) = (2/5)(1/4) = 2/20\\P(RW) = (3/5)(2/4) = 6/20\\P(RR) = (3/5)(2/4) = 6/20\\P(WR) = (2/5)(3/5) = 6/20\)
Because there are three to two more red than white balls in the urn, we would anticipate getting white on eight of them and red on twelve on the first draw.
We would anticipate 2 white and 6 red if the experiment were run eight times if we drew white on the second draw (8 experiments).
We would anticipate 6 white and 6 red on those 12 experiments if we drew red on the first draw (12 experiments), as there would only be 2 white and 2 red remaining on the second draw.
Now, have a look at the 20 tests. There are 2 white-white, 12 red-white, and 6 red-red pairs.
We no longer count the red-red experiments because of the conditional probability, which states, "provided that at least one of them is white." It's as though things never took place.
Given at least one white ball, the conditional probability of two white balls is (1/10) / (7/10) = 1/7.
P(two white balls) / P(at least one white ball) is what this is.
To know more about probability visit:
https://brainly.com/question/30034780
#SPJ4
Simplify 3 ∙ 2x. What is the coefficient?
2
3
6
x
Answers
Answer:
2
Step-by-step explanation:
the coefficient is the number before a variable.
Answer:
6
Step-by-step explanation:
bc i said so
The scores of students on the ACT college entrance examination in a recent year had the normal distribution with mean 18.6 and standard deviation 5.9. Suppose the scores at a local high school have the same distribution as the national scores. If the average score for 25 students who took the test at the local high school was 19.5, what is the probability that the mean score for 25 students randomly selected from all who took the test nationally is 19.5 or higher? 0.2228 0.7772 0.4394 No enough information
Answers
Therefore, the probability that the mean score for 25 students randomly selected from all who took the test nationally is 19.5 or higher is 0.2228 (approximately) which is the complement of 0.7772.
The scores of students on the ACT college entrance examination in a recent year had the normal distribution with mean 18.6 and standard deviation 5.9.
Suppose the scores at a local high school have the same distribution as the national scores. If the average score for 25 students who took the test at the local high school was 19.5, the probability that the mean score for 25 students randomly selected from all who took the test nationally is 19.5 or higher is 0.2228.
The z-score can be calculated as:
z = (x - μ) / (σ / √n)z = (19.5 - 18.6) / (5.9 / √25)z = 1.5254
The probability that the mean score for 25 students randomly selected from all who took the test nationally is 19.5 or higher can be found using the normal distribution table by finding the area to the right of the z-score. This can be represented as:
P(Z > 1.5254) = 0.0666 (approximately)
Therefore, the probability that the mean score for 25 students randomly selected from all who took the test nationally is 19.5 or higher is 0.2228 (approximately) which is the complement of 0.7772.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
Suppose 2 varies jointly with the square of and the cube root of y. If it is know
that Z =
180 when
= 3 and y = 64, what is the value of Z when x = 6
and y = 8?
Answers
We can use the formula for joint variation, which states that a variable varies jointly with two other variables if it is proportional to their product.
In this case, we have:
2 = kxy^(2/3)
where k is a constant of proportionality. To solve for k, we can use the given values of x and y:
2 = k(3)(64^(2/3))
k = 2/(3*64^(2/3))
Now we can use this value of k to find Z when x = 6 and y = 8:
Z = kx^2y^(1/3)
Z = (2/(364^(2/3))) * (6^2)(8^(1/3))
Z ≈ 20.76
Therefore, when x = 6 and y = 8, Z is approximately 20.76.
In this problem, we used the concept of joint variation to find a formula for 2 in terms of x and y. We then solved for the constant of proportionality, k, using the given values of x and y.
Finally, we used this value of k to find Z when x = 6 and y = 8. The process involved using algebraic manipulations and substitution, and the final answer was obtained by plugging in the values of x and y into the formula we derived.
To learn more about constant proportionality click here :
brainly.com/question/12297217?
#SPJ11
Convert 5.87 x 10^5 cg to kg
Show all of your work
Answers
To convert 5.87 x 10^5 centigrams (cg) to kilograms (kg), we need to use the conversion factor of 1 kg = 100,000 cg. Therefore, 5.87 x 10^5 centigrams is equal to 5.87 kilograms.
First, we'll divide 5.87 x 10^5 cg by 100,000 cg/kg to convert centigrams to kilograms:
5.87 x 10^5 cg ÷ 100,000 cg/kg
Next, we'll simplify the expression:
5.87 ÷ 1 x 10^5 ÷ 10^5
Dividing 5.87 by 1 gives us:
5.87 x 10^5 ÷ 10^5
To divide numbers in scientific notation, we subtract the exponents:
5.87 x (10^5 ÷ 10^5)
10^5 ÷ 10^5 equals 1, so the expression simplifies to: 5.87 x 1
Finally, we multiply 5.87 by 1 to get the result: 5.87 kg
To learn more about conversion click here: https://brainly.com/question/28770698
#SPJ11
Do Dilation's always increase the length of line segments?
true or false
i'm marking someone brainliest with the right answer?
Answers
Answer:
true
Step-by-step explanation:
I'm pretty sure it's trur
Pls help
Show workings

Answers
Answer:
2:3
3:2
Step-by-step explanation:
The mean age of 4 women in an office is 28 years old. the mean age of 4 men in an office is 30 years old. what is the mean age(nearest year) of all the people in the office?
Answers
Answer:
29
Step-by-step explanation:
its obvious
Help please! I just don’t understand

Answers
===================================================
Work Shown:
(angle HID) + (angle DIJ) = angle HIJ
(100) + (8x+11) = 21x+7
100+8x+11 = 21x+7
8x+111 = 21x+7
111-7 = 21x-8x
104 = 13x
13x = 104
x = 104/13
x = 8
Use this x value to find angle HIJ
angle HIJ = 21x+7
angle HIJ = 21*8+7
angle HIJ = 175 degrees
---------------------------
Extra info:
You can also use that x value to find angle DIJ
angle DIJ = 8x+11
angle DIJ = 8*8+11
angle DIJ = 75
Then add this to angle HID to get
angle HID + angle DIJ = 100+75 = 175
This matches with angle HIJ = 175
So this confirms angle HID + angle DIJ = angle HIJ which helps confirm our answers.
if the dot product of two nonzero vectors is zero, the vectors must be perpendicular to each other. a) true b) false
Answers
The statement "if the dot product of two nonzero vectors is zero, the vectors must be perpendicular to each other" is true. The dot product of two vectors is zero if and only if the vectors are perpendicular.
The dot product of two vectors is defined as the product of their magnitudes and the cosine of the angle between them. When the dot product is zero, it means that the cosine of the angle between the vectors is zero, which occurs when the vectors are perpendicular.
In other words, the dot product being zero indicates that the vectors are at a 90-degree angle to each other, supporting the statement that they are perpendicular.
Learn more about dot product here: brainly.com/question/23477017
#SPJ11
Rewrite the polynomial in standard form.
5x^3 – 7x^5 + 4x^2 – 3x
Answers
Answer: -7x^5 + 5x^3 + 4x^2 - 3x