Answers
Answer:
L is (2,4) M (3,1,) N(0,4)
Step-by-step explanation:
L 0+2=2 so x is 2
L 1+3=4 so y is 4
M 1+2=3 so x is 3
M -2+3=1 so y is 1
N -2+2=0 so x is 0
N 1+3=4 so y is 4
Related Questions
On a baseball diamond with 90-foot sides, the pitcher's mound is 60.5 feet from home plate. How far is the pitcher's mound from third base? (Round your answer to one decimal place.)
Answers
The distance between third base and the pitcher's mound is roughly 80.0 feet.
To solve this problemThe Pythagorean theorem can be used to resolve this issue.
The pitcher's mound and third base can be thought of as the two ends of a right triangle in this situation, with home plate and third base serving as the hypotenuse. One of the triangle's legs is the distance between home plate and the pitcher's mound.
Let's call the distance between the pitcher's mound and third base "x". Then we can set up the following equation:
\(60.5^2 + x^2 = 90^2\)
Simplifying and solving for x, we get:
\(x^2 = 90^2 - 60.5^2\)
\(x^2 = 6406.25\)
x ≈ 80.0
Therefore, the distance between third base and the pitcher's mound is roughly 80.0 feet.
Learn more about Pythagorean theorem here : brainly.com/question/28981380
#SPJ1
Find the value of x

Answers
Answer: The value of x is 49.
Step-by-step explanation:
To find the value of x, you will first need to cross multiply the fractional variables together.
5x - 80 = 3x + 18
Then, move the numerical term 80 to the right side of this equation and add it to 18.
5x - 80 = 3x + 98
Move 3x to the left side of the equation and subtract it this time to the variable 5x.
2x = 98
Finally, you divide both of the equation's sides by 2 and you will get 49.
x = 49
When you actually add x to this problem, you would get 33/55.
49 - 16/49 +6 = 33/55
You can then simplify 33/55 and get the same answer 3/5.
3/5
Therefore, the value of x for this variable equation with the fractions would be equal to x = 49. Hope this helps!
-From 5th Grader Honors Student
I need help with these two problems 4-155 and 4-156

Answers
a)
\(\frac{12}{5}+\frac{7}{10}=\frac{24}{10}+\frac{7}{10}=\frac{31}{10}\)b)
\(\frac{9}{4}+(-\frac{1}{3})=\frac{9}{4}-\frac{1}{3}=\frac{27-4}{12}=\frac{23}{12}\)c)
\(-\frac{3}{5}+(-\frac{1}{6})=-\frac{3}{5}-\frac{1}{6}=\frac{-18-5}{30}=-\frac{23}{30}\)In a figure, D and E are points on side BC of a△ ABC such that BD = CE and AD = AE. Show that △ABD ≅ △ACE

Answers
Step-by-step explanation:
AD=AE
BD=EC
D=E
....ABD=ACE
Donovan is buying plates and cups for a party do you want to same number of each plate or solid in packs of 8 cups are sold in packs of 12 what is the least number of plates and cups that Donovan can buy
Answers
Answer:
the awnser is 4
Step-by-step explanation:
Convert the rectangular coordinates (-√√2, -√2) into polar form.
Express the angle using radians in terms of 7 over the interval
0 ≤0 < 27, with a positive value of r.

Answers
The polar form of the rectangular coordinates (-√√2, -√2) is (2√(1 + √2), 15π/28)
Converting into polar formTo convert the rectangular coordinates (-√√2, -√2) into polar form, we first need to find the value of r (the radius) and θ (the angle).
r = √((-√√2)^2 + (-√2)^2) = √(2 + 2√2) = 2√(1 + √2)
To find the value of θ, we can use the following formula:
θ = atan(y/x)
where atan is the inverse tangent function, and (x, y) are the rectangular coordinates.
θ = atan(-√2/(-√√2)) = atan(√2) = π/4 radians
However, we need to express the angle in terms of 7 over the interval 0 ≤ θ < 2π/7, with a positive value of r.
To do this, we can add a multiple of 2π/7 to the value of θ until we get an angle in the desired interval.
θ = π/4 + 2π/7 = (7π + 8π)/28 = 15π/28 radians
So the polar form of the rectangular coordinates (-√√2, -√2) is:
(2√(1 + √2), 15π/28)
Learn more on polar form here https://brainly.com/question/29045307
#SPJ1
A skating champion moves along with circumference of a Circe of radius 21 meters in 44 seconds how many seconds will it take her to move along perimeter of a hexagon of side 42 meters
Answers
Answer: Time required to travel along the perimeter of a hexagon = 84seconds
Step-by-step explanation: Given, The radius of the circle = 21m Time taken to travel the circumference of the circle = 44 seconds Side of a hexagon = 42m To find, The time taken to move along the perimeter of a hexagon. Recall the concept Circumference of the circle =2πr The perimeter of a hexagon = 6× length of a side Distance = speed × time Solution Since the radius of the circle = 21m, The circumference of the circle = 2× ×21 = 132m Since time taken to travel 132 m is 44seconds Speed = = = 3m/s Since the length of a side of a hexagon = 42m, the perimeter of a hexagon = 6×42 = 252m Time required to travel along the perimeter of a hexagon = = = 84seconds ∴ Time required to travel along the perimeter of a hexagon = 84seconds
Estimate 11,319+4,865 by first rounding each number to the nearest thousand.
Answers
Answer:
16,000
Step-by-step explanation:
11,319 rounded to the nearest thousand is 11,000.
4,895 rounded to the nearest thousand is 5,000.
11,000 + 5,000 is equal to 16,000.
Solve the system.
-5x - 6y = -17
-3x -5y + 5z = 2
-6x - 5y + z = -13
Enter your answer as an ordered triple.
(?, ?, ?)
Answers
The value of x, y and z in the system equation is (1, 2, 3).
What is the solution of the equation?The solution of the equation can be determined by using Cramer's rule as follows;
[-5 -6 0] = [ -17]
[-3 -5 5] [2 ]
[-6 -5 1] [-13 ]
The determinant of the matrix is calculate as;
Δ = -5 (-5 + 25) + 6(-3 + 30) + 0(15 + 30)
Δ = 62
The x-determinant of the matrix is calculated as follows;
Δx = -17(-5 + 25) + 6(2 + 65) + 0
Δx = 62
The y-determinant of the matrix is calculated as follows;
Δy = -5(2 + 65) + 17(-3 + 30) + 0
Δy = 124
The z-determinant of the matrix is calculated as follows;
Δz = -5(65 + 10) + 6 (39 + 12) - 17(15 - 30)
Δz = 186
The value of x, y and z is calculated as follows;
x = Δx/Δ = 62/62 = 1
y = Δy/Δ = 124/62 = 2
z = Δz/Δ = 186/62 = 3
Learn more about system equations here: https://brainly.com/question/13729904
#SPJ1
Pleasssseeeeee hhhhheeeelllpppp

Answers
Answer:
what can I help you miss
Answer: A' = (1, 5)
B' = (-3, 5)
C' = (-3, 2)
D' = (1, 2)
Step-by-step explanation:
Reflecting across the y-axis provides the opposite x-value.
Z = (x, y) --> Z' = (-x, y)
A = (-1, 5) --> A' = (1, 5)
B = (3, 5) --> B' = (-3, 5)
C = (3, 2) --> C' = (-3, 2)
D = (-1, 2) --> D' = (1, 2)
The height of a tree is 42 inches. After 6 years the height is 15 feet 6 inches. How many inches did the tree grow each year?
Answers
Height of the tree after 6 years,
→ 15 feet 6 inches = 186 inches.
→ 186 - 42 = 144 inches.
Height of the tree after 1st year = 144/6 = 64
∴ The tree grows 24 inches in each year.
Of the population of all fruit flies we wish to give a 90% confidence interval for the fraction which possess a gene which gives immunity to fungal infections. To this end we have obtained a random sample of 400 fruit flies. We find that 280 of the flies in the sample possess the gene. Give the margin of error for the 90% confidence interval. Round your answer to 3 decimal places.
Answers
Answer:
The margin of error for the 90% confidence interval is of 0.038.
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the zscore that has a pvalue of \(1 - \frac{\alpha}{2}\).
The margin of error is of:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
To this end we have obtained a random sample of 400 fruit flies. We find that 280 of the flies in the sample possess the gene.
This means that \(n = 400, \pi = \frac{280}{400} = 0.7\)
90% confidence level
So \(\alpha = 0.1\), z is the value of Z that has a pvalue of \(1 - \frac{0.1}{2} = 0.95\), so \(Z = 1.645\).
Margin of error:
\(M = z\sqrt{\frac{\pi(1-\pi)}{n}}\)
\(M = 1.645\sqrt{\frac{0.7*0.3}{400}}\)
\(M = 0.038\)
The margin of error for the 90% confidence interval is of 0.038.
Use the graph to answer the question.
Determine the translation used to create the image.
A. 7 units to the right
B. 7 units to the left
C. 3 units to the right
D. 3 units to the left

Answers
The correct option is A, we have a translation of 7 units to the right.-
How to determine the translation?To find it, we need to analyze two correspondent vertices.
We can see that vertex A is at (1, 5), while the correspondent vertex A' is at (8, 5)
Taking the difference between that, we will get:
A' - A = (8, 5) - (1, 5) = (8 - 1, 5 - 5) = (7, 0)
The first value gives the horizontal translation and the second the vertical one
So,we have a translation of 7 units to the right, the correct option is A.
Learn more about translations at:
https://brainly.com/question/24850937
#SPJ1
Graph y=4x
Please do it on a graph lol
Answers
thus answers.hooe it's right

Answer:
Look at the screenshot
Step-by-step explanation:
Since it is just y=4x, and there is no b, we start at the origin (0, 0). Now, since slope is rise/run, and 4 can be written as 4/1. we go up 4 and to the right one. You can repeat this as many times as you need. Check the attached screenshot for the graph.

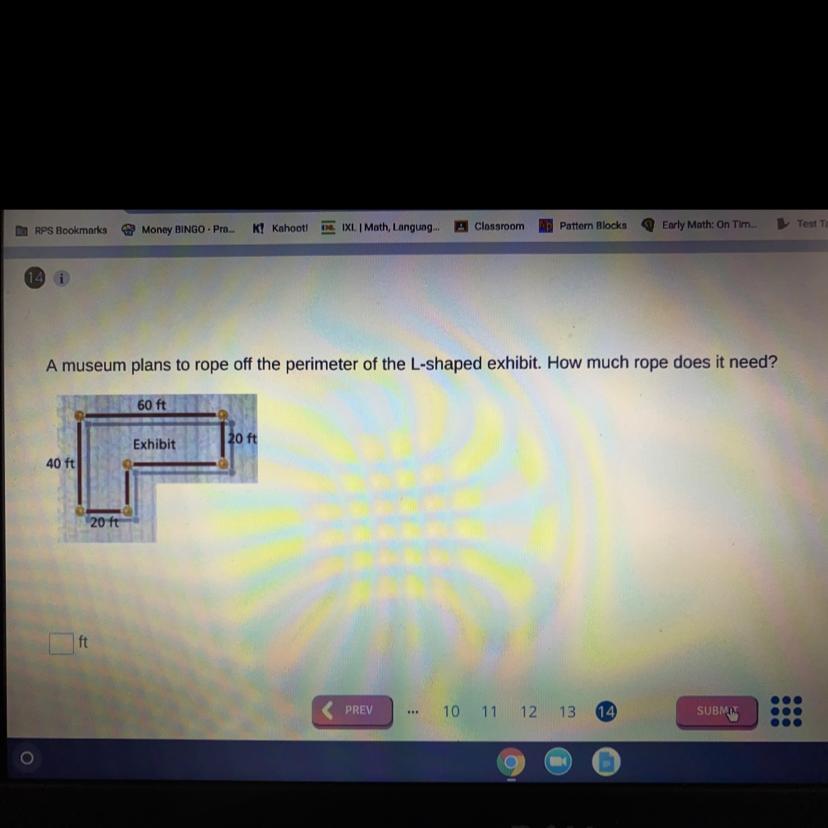
A museum plans to rope off the perimeter of the L shaped exhibit. How much rope does it need
Answers
Answer:
200ft of rope
Step-by-step explanation:
Write an equation of the line with the given slope and y-intercept.
Slope
1
6
, y−intercept (0, −2)
Answers
The equation of line is \(6y=6x$-$12\).
The given slope is \(\frac{1}{6}\).
The \(y $-$\)intercept is \((0, $-$2)\).
We have to write the equation of line using the given slope and \(y $-$\)intercept.
The equation of line with the slope m and \(y $-$\)intercept of \((0,a)\) is \(y=mx+a\).
From the question,
The value of \(m=\frac{1}{6}\)
The value of \(a= $-$2\)
Now putting the value of \(m\) and \(a\) in the equation of line.
\(y=\frac{1}{6}x+( $-$2)\\y=\frac{1}{6}x$-$2\)
Multiply by \(6\) on both side
\(y\times6=6\times(\frac{1}{6}x$-$2)\\6y=6\times\frac{1}{6}x$-$6\times2\\6y=6x$-$12\)
The equation of line is \(6y=6x$-$12\).
To learn more about slope and \(y-\)intercept form here link
https://brainly.com/question/12952118
#SPJ1
Robert is going on a 2-day canoeing trip with his outdoor adventure group. Robert paddled at a constant sped and travels 3/4 of a mile in 15 minutes.
a. Create a table to determine how long it takes Robert to canoe 1 mile.
b. On the first day of the trip, Robert canoes for 3 hours. How far did Robert travel?
c. On the second day of the trip, Robert travels 6 miles down the river. How many hours did he send paddling?
d. Another member of the group, Matthew, can canoe 3/2 miles in 45 minutes. Who is traveling at a faster rate, Robert or Matthew? Explain your reasoning. (NO LINKS)
Answers
Answer:
i think the Answer is D
Step-by-step explanation:
There are really questions to answer .
A researcher wishes to see if the average weights of newborn male infants are higher than the
average weights of newborn female infants. She selects a random sample of 12 male infants and
finds the mean weight is 7.70 pounds. She selects a random sample of 9 female infants and finds
that the mean Leight is 7.80 pounds. Assume that the variables are normally distributed and the
population standard deviation is 0.5 for each group.
Using alpha=0.05 to test if the mean weight of the males is higher than the mean weight of the
females, the pvalue of the test is:
Answers
Answer:
The p-value is \(p-value = 0.62578\)
Step-by-step explanation:
From the question we are told that
The sample size of male infant is \(n_1 = 12\)
The sample size of female infant is \(n_2= 9\)
The sample mean of male infant is \(\= x_1 = 7.70 \ lb\)
The sample mean of female infant is \(\= x_2 = 7.80 \ lb\)
The population standard deviation is \(\sigma = 0.5\)
The significance level is \(\alpha = 0.05\)
The null hypothesis is \(H_o : \mu_ 1 = \mu_2\)
The alternative hypothesis is \(H_1 : \mu_1 > \mu_2\)
The test statistics is mathematically represented as
\(t =\frac{\= x_1 - \= x_2 }{\sqrt{\frac{\sigma }{n_1} } + \frac{\sigma }{n_2} } }\)
=> \(t = \frac{7.70 -7.80}{\sqrt{\frac{0.5 }{12} } + \frac{0.5 }{9} } }\)
=> \(t = -0.3207\)
From the z-table the p-value is obtained, the value is
\(p-value = P(Z > -0.3207) = 0.62578\)
\(p-value = 0.62578\)
At a local college, only 30% of students live off campus. Of those who live off campus, 62% of those students get a part-time job. Of those who live on campus, 65% work part-time. The tree diagram shows how the college students are divided into subgroups.
The tree diagram shows college students branching off into two categories, off campus and on campus students. Off campus students branches off into two sub-categories, work part-time and do not work. On campus branches off into two subcategories, work part-time and do not work.
What is the percentage of students who live on campus who do not have a part-time job?
18.6%
24.5%
35%
38%
Answers
Answer:
24.5%
Step-by-step explanation:
Given
P(Off-Campus) = 0.30
P(Part-Time Job | Off-Campus) = 0.62
P(Part-Time Job | On-Campus) = 0.65
Inferred
P(On-Campus) = 0.70
P(No Part-Time Job | Off-Campus) = 0.38
P(No Part-Time Job | On-Campus) = 0.35
Calculation
P(No Part-Time Job | On-Campus) = P(No Part-Time Job ∩ On-Campus)/P(On-Campus)
0.35 = P(No Part-Time Job ∩ On-Campus)/0.70
0.245 = P(No Part-Time Job ∩ On-Campus)
Therefore, 24.5% of students that live on campus do not have a part-time job.
Pls help!!!
Question in the picture

Answers
Answer:
-7, -\(\pi\) -\(\sqrt{3}\) , 9
Step-by-step explanation:
Answer:
The answer will be... -7, -\(\pi\), -\(\sqrt{3}\), 9Step-by-step explanation:
Hope this helped you.Petra jogs 6 miles in 42 minutes. At this rate, how long would it take her to jog 8 miles?
Answers
Distance 1 / Time 1 = Distance 2 / Time 2
Using the information given:
6 miles / 42 minutes = 8 miles / Time 2
To solve for Time 2, we can cross-multiply and then divide:
6 miles * Time 2 = 8 miles * 42 minutes
6 * Time 2 = 8 * 42
6 * Time 2 = 336
Now, we divide both sides by 6 to isolate Time 2:
Time 2 = 336 / 6
Time 2 = 56 minutes
Therefore, it would take Petra 56 minutes to jog 8 miles at the same rate.
Answer:
56 minutes
Step-by-step explanation:
We can use proportions to solve.
6 miles 8 miles
------------ = ------------------
42 minutes x minutes
Using cross products.
6x = 42 *8
Divide each side by 6
x = 42/6 * 8
x = 7*8
x = 56
Help me with questions please

Answers
Hope this helped
Greta currently works 45 hours per week and earns a weekly salary of $729. She
will soon be starting a new job where her salary will be increased by 10% and her hours reduced by 10%.
How much more will she be earning per hour at her new job?
PLEASE SHOW YOUR WORK!!
Answers
Answer:
Greta will be earning 3.6/h more at her new job.
Step-by-step explanation:
To find the difference subract Greta‘s salary from her current job from Greta’s salary from her future job.
To find Greta’s salary (numerator) at her future job divide her current weekly salary ($729) by 45h then multiply that answer (16.2) by the increase in salary 10% or 1.1. You should end up with $17.82- this is your numerator. To find the denominator divide her current hours (45h) by 45 then multiply that answer (1) by 0.9 which is the 10% decrease in hours. Now you have a fraction ($17.82/0.9) then multiply that fraction by 1.1/1.1 to get the denominator to 1 hour so you can subtract the fractions. You should end up with $19.8/h.
Now subtract Greta’s current salary ($16.2/h)- you just take the numbers from the first part before you increase or decrease- from her future salary ($19.8/h), you will end up with 3.6/h.
I was challenged to write this in a single equation:
[((($729\45h)x1.1)/((45h\45)x0.9))x1.1/1.1]-[($729\45h)/(45h\45)]
=$3.6/h
/ means a fraction bar
\ means division
Also I am just a student so please tell me if you find any mistakes I could fix or any suggestions to make this a better explanation, and if you have any questions ask away.
Given (x – 7)2 = 36, select the values of x.
x = 13
x = 1
x = –29
x = 42
Answers
Answer:
x=1,13
Step-by-step explanation:
(x – 7)^2 = 36
Take the square root of each side
sqrt((x – 7)^2) = sqrt(36)
x-7 = ±6
x-7 = 6 x-7 =-6
Add 7 to all sides
x-7+7 = 6+7 x-7+7 = -6+7
x = 13 x=1
-50 POINTS- Already asked 3 times someone help pls. Don’t guess either.

Answers
Answer:
To find the coordinates of the point on the x-axis that is reflected over the x-axis from the point P, you can use the formula (x, -y). In this case, the x-coordinate of point P is 4, so the x-coordinate of the reflected point will also be 4. The y-coordinate of point P is 7, so the y-coordinate of the reflected point will be -7. Therefore, the coordinates of the reflected point are (4, -7).
7- At the school car wash, Kelly washes a car in 13 minutes, and Libby washes a car in 17 minutes, How many more minutes does it take Kelly to wash a car alone than it takes Kelly and Libby to wash a car when working together? Express your answer as a decimal to the nearest tenth.
Answers
Kelly will take 5.64 minutes more to wash the car as compared to Kelly and Libby when they are working together
Time taken by Kelly to wash the car = 13 minutes
Time taken by Libby to wash the car = 17 minutes
Time taken by Kelly and Libby to wash the car together:
LCM of 13 and 17 is 221. So, the total work required to be done is 221 units
Hence, Kelly does 17 units of work each minute and Libby does 13 units of work each minute
If both work together, they will finish the work in = Total work required to be done/ Work done in a minute by Kelly + Work done in a minute by Libby
= 221/(17+13)
= 221/30 = 7.36 minutes
The extra time taken by Kelly working alone = 13-7.36 = 5.64 minutes
Learn more about work and time:
https://brainly.com/question/3854047
#SPJ1
A student takes a subway to a public library. The table shows the distance d (in miles) the student travels in t minutes. Determine whether the data can be modeled by a linear, exponential, or a quadratic function and then select a function rule to model the situation.
t
d
1
0.83
2
1.66
3
2.49
4
3.32
5
4.15
Answers
The linear function that models the situation is given as follows:
d = 0.85t.
What is a proportional relationship?A proportional relationship is a relationship in which a constant ratio between the output variable and the input variable is present.
The equation that defines the proportional relationship is a linear function with slope k and intercept zero given as follows:
y = kx.
The slope k is the constant of proportionality, representing the increase or decrease in the output variable y when the constant variable x is increased by one.
The constant ratio for this problem is given as follows:
k = 0.83, as each division of d by t has a result of 0.83.
Hence the equation is given as follows:
d = 0.83t.
A similar problem, also featuring proportional relationships, is presented at https://brainly.com/question/7723640
#SPJ1
an airlane is on heading of 075 degree at 250 km/h wind is blowing from 300 Determine the resultan velocity of the airplane using cartesian vectors and state the ground speed and bearing of the resultant
Answers
The airplane's groundspeed is approximately 242.25 km/h, and the resultant bearing is approximately 55.04° (relative to true north, measured clockwise).
How to solve for the airplane's groundspeed
To determine the resultant velocity of the airplane, we need to break down the airplane's velocity and the wind's velocity into their respective components and add them. Let's assume that the angles are measured clockwise from true north.
Let's denote:
Vp = airplane's speed = 250 km/h
θp = airplane's heading = 075 degrees
Vw = wind's speed = 85 km/h
θw = wind's heading = 300 degrees
We can then find the eastward (x) and northward (y) components of the velocities:
For the airplane:
Vpx = Vp * cos(θp) = 250 * cos(75 degrees) = 64.95 km/h
Vpy = Vp * sin(θp) = 250 * sin(75 degrees) = 241.92 km/h
For the wind:
Vwx = Vw * cos(θw) = 85 * cos(300 degrees) = 73.60 km/h
Vwy = Vw * sin(θw) = 85 * sin(300 degrees) = -42.50 km/h
We then sum the x and y components of the two velocities to find the resultant velocity components:
Vrx = Vpx + Vwx = 64.95 km/h + 73.60 km/h = 138.55 km/h
Vry = Vpy + Vwy = 241.92 km/h - 42.50 km/h = 199.42 km/h
The magnitude of the resultant velocity, which represents the groundspeed (Vr), is found using the Pythagorean theorem:
Vr = sqrt((Vrx)^2 + (Vry)^2) = sqrt((138.55)^2 + (199.42)^2) = 242.25 km/h
The bearing (θr) of the resultant velocity (relative to north) can be found using inverse tangent:
θr = atan2(Vry, Vrx) = atan2(199.42, 138.55) = 55.04 degrees
Therefore, the airplane's groundspeed is approximately 242.25 km/h, and the resultant bearing is approximately 55.04° (relative to true north, measured clockwise).
Read more on resultant velocity here https://brainly.com/question/4945130
#SPJ1
how many solutions does the eqaution below have? 4x-3-2x+5=6-3x+2+5x
Answers
Answer:
4x - 3 - 2x + 5 = 6 - 3x + 2 + 5x
2x + 2 = 2x + 8
2 ≠ 8, so this equation has no solutions.
Answer:
No solution
Step-by-step explanation:
Given:
\(4x-3-2x+5=6-3x+2+5x\)
rearrange terms so like terms are together
\(4x-2x-3+5=6+2-3x+5x\)
combine like terms
\(2x+2=8+2x\)
subtract 2x to both sides
\(2\neq 8\)
2 doesn't equal 8, meaning that there are 0 solutions to this problem.
Hope this helps! :)
A package of 3 pairs of gloves costs $16.17. What is the unit price per pair of gloves. PLS HELP ASAP
Answers
Since 3 gloves is $16.17, divide 16.17 by 3 to get $5.39