What is
(
f
∘
g
)
(
x
)
if
f
(
x
)
=
2
x
+
3
and
g
(
x
)
=
x
4
?
(
f
∘
g
)
(
x
)
=
3
4
x
+
1
2
(
f
∘
g
)
(
x
)
=
1
2
x
+
3
4
(
f
∘
g
)
(
x
)
=
1
2
x
+
3
2
Answers
Answer: -11 and 0
Step-by-step explanation:
If the functions f(x) = 2x + 3 and g(x) = x⁴ then the (f ∘ g)(x) is 2(x⁴) + 3
To find (f ∘ g)(x), we need to substitute g(x) into f(x) and simplify.
Given function f(x) = 2x + 3.
g(x) = x⁴
Substituting g(x) into f(x):
(f ∘ g)(x) = f(g(x))
(f ∘ g)(x) = f(x⁴)
Now let us find the value of f(x⁴).
(f ∘ g)(x) = 2(x⁴) + 3
Therefore, the correct answer is (f ∘ g)(x) = 2x⁴ + 3.
To learn more on Functions click:
https://brainly.com/question/30721594
#SPJ7
Complete question.
What is ( f∘g )(x) if f(x) = 2x+3 and g(x) = x⁴ ?
Related Questions
Simplify the following expression:
(i-3) +6i-3(8 - i)
Answers
Answer:
10i-27
Step-by-step explanation:
(i-3)+6i-3(8-i)
(i-3)+6i-24+3i
(i-3)+9i-24
10i-3-24
10i-27
Answer:
-27 + 10i
Step-by-step explanation:
What is the reference angle for 289°?
Answers
Answer:
71º
Step-by-step explanation:
360 - 289 = 71º
Explain how to evaluate 3 to the fourth power
Answers
Answer:
3 to the fourth power would basically mean 3 x 3 x 3 x 3
Step-by-step explanation:
Alot of people get this confused with 3 x 4 but when multuply to the power of four its 3 x 3 x 3 x 3 which is 81
Brainliest?
I need help solving this math problem step by step.
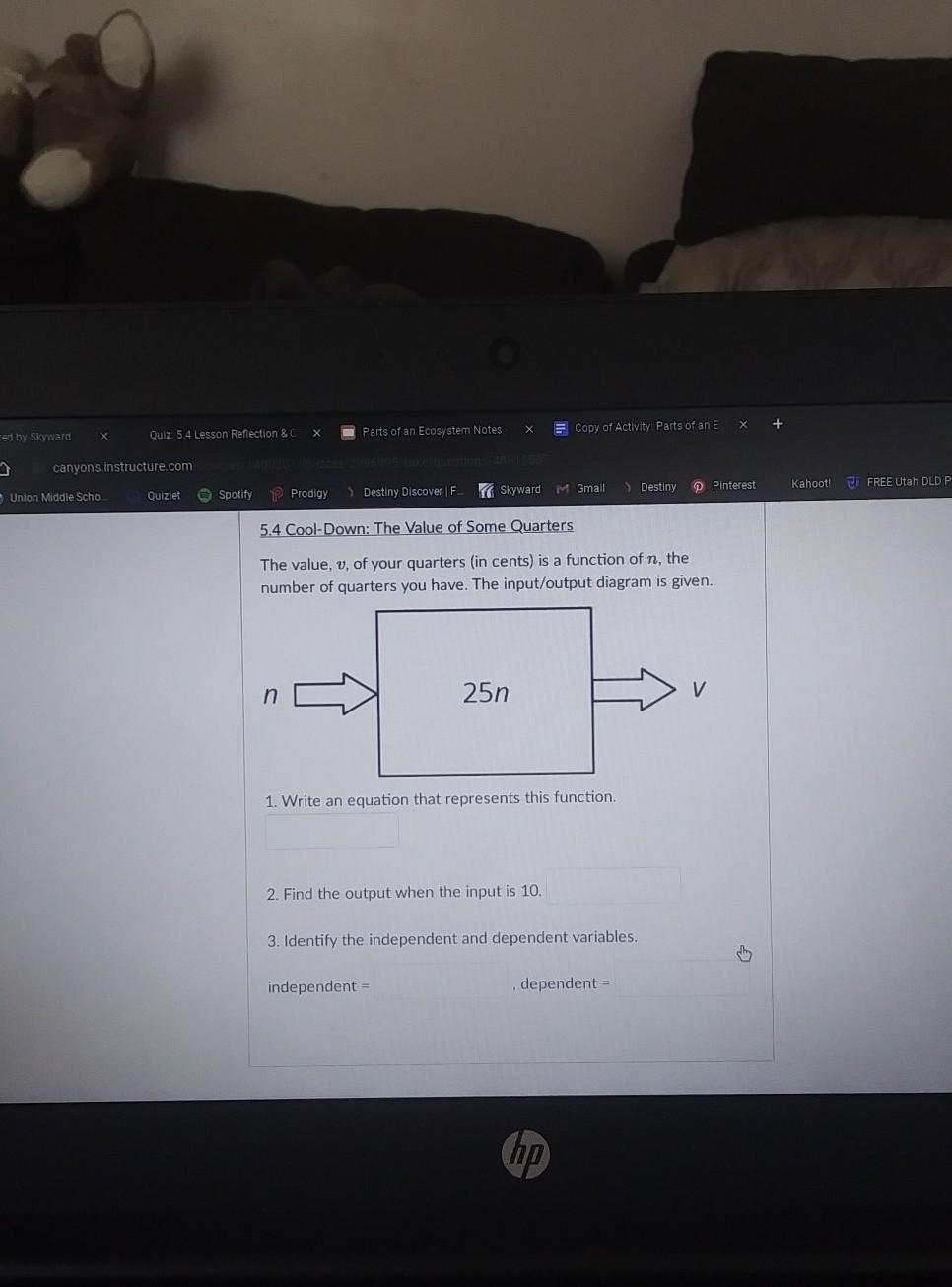
Answers
Answer:
\(\begin{gathered} 1.\text{ }v=25n \\ 2.\text{ }v=250 \end{gathered}\)Step by step explanation:
By the input/output diagram we can state that:
\(v=25n\)Then, to find the output when n=10, substitute in the function above:
\(\begin{gathered} v=25(10) \\ v=250 \end{gathered}\)1 2 Q8 (x - 3)2 + (v +0.5)2 = 1 The result of a transformation of circle A using the rule (x,y) → (1 +4, y - 1), followed by a dilation of centered at the origin will result in which crcle (x - 2)2 + 12 = 4 from the choices below? (x + 2)2 + (1 - 1)2 = 4 (x + 1)2 + (1 -0.5)2 = 2 A
Answers
first we write the equation of the incial circle
general equation is
\((x+a)^2+(y+b)^2=r^2\)where (-a,-b) is the origin and r the radious
From the graph, the origin is (2,0) and radious 2 units
then the equation is
\(\begin{gathered} (x-2)^2+(y-0)^2=2^2 \\ \\ (x-2)^2+y^2=2^2 \end{gathered}\)now apply the trasnformations
(x+4 , y-1)
we add 4 to x and subtrat 1 to y
\(\begin{gathered} (x-2+4)^2+(y-1)^2=2^2 \\ \\ (x+2)^2+(y-1)^2=2^2 \end{gathered}\)dilation of 1/2
multiply the radious by the dilation
\((x+2)^2+(y-1)^2=(2\times\frac{1}{2})^2\)Finally the equation of the new circle is
\((x+2)^2+(y-1)^2=1\)An advertisement for a popular weight-loss clinic suggests that participants in its new diet program lose, on average, more than 10 pounds. A consumer activist decides to test the authenticity of the claim. She follows the progress of 18 women who recently joined the weight-reduction program. She calculates the mean weight loss of these participants as 10.8 pounds with a standard deviation of 2.4 pounds. It may be assumed that the weight loss of participants to the weight-reduction program is normally distributed.
a) set up the competing hypotheses to test the advertisement's claim
b) at the 5% significance level, what is the critical value(s)? specify the decision rule
c) what does the consumer activist conclude?
Answers
Testing the hypothesis, it is found that:
a)
The null hypothesis is: \(H_0: \mu \leq 10\)
The alternative hypothesis is: \(H_1: \mu > 10\)
b)
The critical value is: \(t_c = 1.74\)
The decision rule is:
If t < 1.74, we do not reject the null hypothesis.If t > 1.74, we reject the null hypothesis.c)
Since t = 1.41 < 1.74, we do not reject the null hypothesis, that is, it cannot be concluded that the mean weight loss is of more than 10 pounds.
Item a:
At the null hypothesis, it is tested if the mean loss is of at most 10 pounds, that is:
\(H_0: \mu \leq 10\)
At the alternative hypothesis, it is tested if the mean loss is of more than 10 pounds, that is:
\(H_1: \mu > 10\)
Item b:
We are having a right-tailed test, as we are testing if the mean is more than a value, with a significance level of 0.05 and 18 - 1 = 17 df.
Hence, using a calculator for the t-distribution, the critical value is: \(t_c = 1.74\).
Hence, the decision rule is:
If t < 1.74, we do not reject the null hypothesis.If t > 1.74, we reject the null hypothesis.Item c:
We have the standard deviation for the sample, hence the t-distribution is used. The test statistic is given by:
\(t = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}}\)
The parameters are:
\(\overline{x}\) is the sample mean. \(\mu\) is the value tested at the null hypothesis. s is the standard deviation of the sample. n is the sample size.For this problem, we have that:
\(\overline{x} = 10.8, \mu = 10, s = 2.4, n = 18\)
Thus, the value of the test statistic is:
\(t = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}}\)
\(t = \frac{10.8 - 10}{\frac{2.4}{\sqrt{18}}}\)
\(t = 1.41\)
Since t = 1.41 < 1.74, we do not reject the null hypothesis, that is, it cannot be concluded that the mean weight loss is of more than 10 pounds.
A similar problem is given at https://brainly.com/question/25147864
Find the output, y, when the input, x, is -9.
y =

Answers
Answer:
when x=-9, y=1
Step-by-step explanation:
the graph shows when the x is at -9, the y is at 1

Which of these is not a possible r-value?
ОА. 1.2
Ов. 0.5
Ос. -0.75
OD. -0.1
Answers
Answer:
Step-by-step explanation:
A
The logarithmic property
\( log_{b}(m) - log_{b}(n) \)
=
\( log_{b}( \frac{m}{n} ) \)
can be proven by using which exponential property.
Answers
Answer:
using divisional law of indices logab-logan=log(b/n)therefore logbM-logbN=logb(M/N)
help asap! i will give brainliest!



Answers
#1
\(\\ \sf\longmapsto f(x)=5x-1\)
\(\\ \sf\longmapsto f(0.2)=5(0.2)-1=1-1=0\)
#2
\(\\ \sf\longmapsto f(x)=89\)
\(\\ \sf\longmapsto 5x-1=89\)
\(\\ \sf\longmapsto 5x=89+1=90\)
\(\\ \sf\longmapsto x=\dfrac{90}{5}\)
\(\\ \sf\longmapsto x=18\)
You pick a card at random, put it back, and then pick another card at random. 5 6 7 8 What is the probability of picking a prime number and then picking a prime number? Simplify your answer and write it as a fraction or whole number.
Answers
In fraction form, the answer is 1/4, which represents the simplified probability of the given event occurring.
To find the probability of picking a prime number and then picking another prime number, we first need to determine the total number of possible outcomes and the number of favorable outcomes.
Given the four numbers: 5, 6, 7, and 8, we can see that there are two prime numbers (5 and 7) and two non-prime numbers (6 and 8).
The total number of possible outcomes is 4 since there are four cards to choose from.
Now, let's consider the favorable outcomes, which are picking a prime number and then picking another prime number.
The probability of picking a prime number on the first draw is 2/4, as there are two prime numbers out of the four total cards.
Since we replace the card before the second draw, the probability of picking a prime number on the second draw is also 2/4.
To find the probability of both events occurring, we multiply the individual probabilities:
(2/4) * (2/4) = 4/16 = 1/4
Therefore, the probability of picking a prime number and then picking another prime number is 1/4.
For more such questions on probability
https://brainly.com/question/24756209
#SPJ8
An airplane has an airspeed of 528 mi/hr bearing 25° west of north. Which of the following vectors best describes the path of the airplane? O v= 528 cos(155°)i + 528 sin(1550); O v = 25 cos(528°)i + 25 sin(528°); O None of these O v = 528 cos(25°)i + 528 sin(259); O v = 528 cos(115°)i + 528 sin(115)
Answers
An airplane has an airspeed of 528 mi/hr bearing 25⁰ west of north. The path can be described as a vector v = (528 cos 115⁰) i + (528 sin 115⁰) j
Suppose we have a vector with magnitude v and angle α with the positive x-axis, then the vector can be expressed as its component as:
vx = v cos α
vy = v sin α
or
v = vx i + vy j
v = (v cos α) i + (v sin α) j
In the given problem, the magnitude is 528, while the angle is:
α = 25⁰ west of north = 25⁰ + 90⁰ = 115⁰
Hence,
vx = 528 cos 115⁰
vy = 528 sin 115⁰
v = (528 cos 115⁰) i + (528 sin 115⁰) j
Learn more about vector here:
https://brainly.com/question/25705666
#SPJ4
g(x) = -5x + 2. need help fr
Answers
Answer:
g= −5x+2/x
x = 2/g+5
Step-by-step explanation:
Ronald was 1.5 times olderthan Megan. If Ronald was 27years old, how old is Megan?Write an equation to solve.
Answers
Solution:
Let x represent Ronald's age, and y represent Megan's age.
Thus,
\(\begin{gathered} x\Rightarrow Ronald^{\prime}s\text{ age} \\ y\Rightarrow Megan^{\prime}s\text{ age} \end{gathered}\)Given that Ronald was 1.5 times older than Megan, we have the equation to be represented
\(x=1.5y\text{ ---- equation 1}\)If Ronald was 27 years old, we have
\(x=27\)Substituting the value of 27 for x into equation 1, we have
\(\begin{gathered} 27=1.5y \\ solve\text{ for y by dividing both sides by the coefficient of y,} \\ \frac{27}{1.5}=\frac{1.5y}{1.5} \\ \Rightarrow y=18 \end{gathered}\)This implies that Megan's age is
\(18\text{ years}\)Which expression is equivalent to the given expression? 2x^2 - 14x - 24
Answers
Answer:
\( 2( {x}^{2} - 7x - 12)\)
Step-by-step explanation:
\( \huge \: 2x^2 - 14x - 24 \\ \huge \: = 2( {x}^{2} - 7x - 12)\)
A scale drawing for an apartment is shown below.
In the drawing, 5 cm represents 6 m.
Assuming the bedroom is rectangular, find the area of the real bedroom.
Answers
Answer:
16
Step-by-step explanation:
3x^3-2x^2+7x+9 divided by x^2-3x
Answers
The quotient is 3x + 7, and the remainder is (28x + 9) / (x^2 - 3x).
What is Division?A division is a process of splitting a specific amount into equal parts.
We have to find 3x³-2x²+7x+9 divided by x²-3x
3x³-2x²+7x+9 is the dividend and x²-3x is the divisor.
The steps to solve this are given below.
Step 1: Take the first digit of the dividend from the left. Check if this digit is greater than or equal to the divisor.
Step 2: Then divide it by the divisor and write the answer on top as the quotient.
Step 3: Subtract the result from the digit and write the difference below.
Step 4: Bring down the next digit of the dividend (if present).
Step 5: Repeat the same process.
Hence, the quotient is 3x + 7, and the remainder is (28x + 9) / (x^2 - 3x).
To learn more on Division click:
https://brainly.com/question/21416852
#SPJ9

Out of 190 CDs tested, 26 are defective. Estimate the number of defective CDs in a batch of 1000.
Answers
Divide the number of defective by the number checked:
26/190 = 0.1368
Multiply that by 1000:
0.1368 x 1000 = 136.8
Round up to 137
Out of 1000 cd’s 137 would be defective
What is the perimeter of a rectangle 15x4
Answers
Answer:
38
Step-by-step explanation:
perimeter = 2(l+b)
Where l is the length of the rectangle
b is the breadth of the rectangle
P = 2(15+4)
P = 2 × 19
P = 38
Find the course and ground speed for the following: Track 090°, airspeed 300km/h; wind 060°, 50km/h.
Answers
The course of the airplane relative to true north is 094°, and the ground speed is 344.2 km/h.
What is the ground speed of the plane?The horizontal and vertical component of the airspeed is calculated as follows;
Vx = 300 cos(30) = 259.8 km/h
Vy = 300 x sin(30) = 150 km/h
The horizontal and vertical component of the wind velocity is calculated as follows;
Vx = 50 cos(60) = 25 km/h
Vy = 50 sin(60) = 43.3 km/h
To find the resultant velocity, we can add the x and y components separately:
Vx = 259.8 km/h + 25 km/h = 284.8 km/h
Vy = 150 km/h + 43.3 km/h = 193.3 km/h
The magnitude of the resultant velocity is calculated as;
V = √(284.8² + 193.3²)
V = 344.2 km/h
The direction of the resultant velocity is calculated as;
θ = arc tan (193.3/284.8)
θ = 34.2⁰
The resultant direction to true north is calculated as;
track = 34.2 + 60 = 94.2°
Learn more about ground speed here: https://brainly.com/question/24208048
#SPJ1
PLEASE HELP AS SOON AS POSSIBLE

Answers
Answer:
B
Step-by-step explanation:
Yes, because for each input there is exactly one output. You can have two of the same x values but you cannot have 2 of the same y values. if you have two of the same y values, it is not a function as it doesn't pass the vertical line test.
College level Trigonometry any help will do!!

Answers
The magnitude of the resultant force is approximately 9.07 lb.
We have,
To use the parallelogram rule to find the magnitude of the resultant force for the two forces, we first draw a diagram:
B (11 lb)
/|
/ |
/ |
/ |
/ |
/ |
/θ |
/ |
A (7 lb) |
\ |
\ |
\ |
\ |
\ |
\ |
\ |
\|
C
where A and B are the magnitudes of the given forces, and θ is the angle between them.
Using the parallelogram rule, we draw a parallelogram with sides AB and BC:
B (11 lb)
/|
/ |
/ |
/ |
/ |
/ |
/θ |
/ |
A (7 lb) D
\ |
\ |
\ |
\ |
\ |
\ |
\ |
\|
C
The diagonal BD represents the magnitude and direction of the resultant force.
To find its magnitude, we use the Law of Cosines:
BD^2 = AB^2 + BC^2 - 2(AB)(BC)cos(θ)
BD^2 = (7 lb)^2 + (11 lb)^2 - 2(7 lb)(11 lb)cos(133 degrees)
BD^2 = 49 + 121 - 2(77)cos(133 degrees)
BD^2 = 170 - 154cos(133 degrees)
BD ≈ 9.07 lb (rounded to two decimal places)
Therefore,
The magnitude of the resultant force is approximately 9.07 lb.
Learn more about the parallelogram rule here:
https://brainly.com/question/28244212
#SPJ1
quentin is filling a glass that holds 1 3/4 cups of water. he is using 1/4 cup measuring cup. how many times will he have to fill the smaller measuring cup to equal 1 3/4 cups?
Answers
Answer: 7 lol
Step-by-step explanation:
The number of times he will have to fill the smaller measuring cup to equal 1 3/4 cups is 7 times.
What is a fraction?A fraction is written in the form of a numerator and a denominator where the denominator is greater that the numerator.
Example: 1/2, 1/3 is a fraction.
We have,
Glass holds = 1(3/4) cups of water
One cup holds = 1/4 cup of water
Now,
The number of 1/4 cups needed to fill the 1(3/4) cups of water glass.
1/4 x C = 1(3/4)
C/4 = 7/4
C = 7/4 x 4
C = 7
Thus,
The number of times the smaller cup fills the glass is 7.
Learn more about fractions here:
https://brainly.com/question/24370499
#SPJ2
What is 1/5 divided by 4?
Answers
Answer:
0.8
Step-by-step explanation:
Answer:
I believe that answer is 0.05
Step-by-step explanation:
Matthew eat 8 crackers for a snack each weekday. On Friday, he drops 4 and only eats 4. What
is the total number of crackers Matthew eats during the week?
Answers
Answer:
36 crackers
Step-by-step explanation:
If he normally eats 8 crackers every weekday, he consumes about 40 crackers.
On the last day however, he dropped 4, so he only ate 4.
8 * 4 = 32
32+ 4
= 36
Choose all the expressions that are equal to 34 × 8,010.
A. 8,010 × 34
B. 34 × (801 × 102)
C. 30 × 4 × 8,010
D. 34 × (8,000 + 10)
E. (30 + 4) × 8,010
Answers
A. 8,010 × 34
D. 34 × (8,000 + 10)
E. (30 + 4) × 8,010
g (x)=√-3x+6
Look at photo please

Answers
Answer:
\((-\infty,2)\)
Step-by-step explanation:
Since \(-3x+6\nless 0\), then \(x\ngtr 2\), therefore, the domain of the function is \((-\infty,2)\).
A particular fruit's weights are normally distributed, with a mean of 720 grams and a standard deviation of 38 grams. The heaviest 19% of fruits weigh more than how many grams? Give your answer to the nearest gram.
Answers
Answer: The heaviest 19% of fruits weigh more than 753grams.
Step-by-step explanation:
Let X = fruit's weights that are normally distributed.
Given: \(\mu=720,\ \ \ \sigma=38\)
To find : x such that P(X>x)=19%
i.e. P(X<x) = 81% [100%-19%=81%]
i.e. P(X<x) = 0.81
\(P(\dfrac{X-\mu}{\sigma}<\dfrac{x-720}{38})=0.81\)
Since, \(Z=\dfrac{X-\mu}{\sigma}\) and from z-table the z value for p-value of 0.81 (one -tailed) = 0.8779
\(\dfrac{x-720}{38}=0.8779\\\\\Rightarrow\ x-720 =38\times0.8779\\\\\Rightarrow\ x-720 =33.36\\\\\Rightarrow\ x = 33.36+720=753.36\approx753\)
Hence, the heaviest 19% of fruits weigh more than 753grams.
Find the measure of the circumscribed angle.

Answers
Applying the tangent theorem, the measure of the circumscribed angle is calculated as: m<BCD = 58°
How to Find the Measure of the Circumscribed Angle?To find the measure of the circumscribed angle, let us remember the theorem regarding the angles formed by intersecting tangents: "When two tangents intersect at a point outside a circle, the angle between them is equal to half the positive difference of the measures of the arcs intercepted by the angle."
Therefore:
m<BCD = 1/2(238 - 122)
m<BCD = 1/2(116)
m<BCD = 58°
Learn more about the circumscribed angle on:
https://brainly.com/question/29164079
#SPJ1
You want to determine the percentage of seniors who drive to campus. You take a random sample of 125 seniors and ask them if they drive to campus. Your 95% confidence interval turns out to be from 0.69 to 0.85. Select each correct interpretation of this situation. There might be no, one, or more than one correct statement. Explain, the reason if it is not a correct interpretation.
Answers
Answer:
The statements that are true are: A, B, F, G, and H.
Step-by-step explanation:
The statements are:
A. A 90% confidence interval would be narrower than the interval given.
TRUE.
The less confidence, the less conservative is the interval and the narrower it can be. So this statement is true.
B. You are 95% confident that the proportion of all seniors who drive to campus is in the interval from .69 to .85.
TRUE.
That is the definition of confidence interval.
C. 95% of all seniors drive to campus from 69% to 85% of the time, and the rest drive more frequently or less frequently.
FALSE.
The confidence interval only has meaning referred to the population proportion, not the individual values. So we can not claim this is true.
D. All seniors drive to campus an average of 77% of the time.
FALSE.
The average is expected to be, with 95% confidence, between 0.69 and 0.85. The sample proportion is 0.77*, and this outcome is used to calculate the confidence interval, but we don't know if the true average is 0.77.
*Sample proportion:
\(p=(LL+UL)/2=(0.69+0.85)/2=1.54/2=0.77\)
E. You are 95% confident that the proportion of seniors in the sample who drive to campus is between .69 and .85.
FALSE.
The sample proportion is known and it is 0.77.
F. 77% of the seniors in your sample drive to campus.
TRUE.
This is the sample proportion.
G. If the sampling were repeated many times, you would expect 95% of the resulting samples to have a sample proportion that falls in the interval from .69 to .85.
TRUE.
This is a property of the confidence intervals.
H. If the sampling were repeated many times, you would expect 95% of the resulting confidence intervals to contain the proportion of all seniors who drive to campus.
TRUE.
This is a property of the confidence intervals.