What is 14/20 as a percent
Answers
Remember 'bout :
Percent is /100
So :
14 ×5 70
-------- = ----- -
20×5 100
70 %
Im sorry if im wrong
Related Questions
please help what is (2n-7)
Answers
Answer:
The answer is 1
Step-by-step explanation:
3. What is the area of the triangle below? (1 point) O 6.0 ft2 O 8.6 ft2 O 15.0 ft? O 17.2 ft2

Answers
Answer:
A ≈ 8.6 ft²
Step-by-step explanation:
the area (A) of the triangle is calculated as
A = \(\frac{1}{2}\) × 7 × 3 × sin55°
= \(\frac{1}{2}\) × 21 × sin55°
= 10.5 × sin55°
≈ 8.6 ft²( to 1 dec. place )
Fine the value of x and y

Answers
Answer:
x = 62 and y = 28
Step-by-step explanation:
Solving for x:
\(47+15 = 62\\180-62 = 118\\180 - 118 = 62 \\x = 62\)
Solving for y:
\(62 + 90 =152\\180-152=28\\y = 28\)
Find the area if the shaded region. REALLY URGENT m!

Answers
i hope this helps you

What is the speed, in miles per hour, of an object traveling at 66 feet per second?
Answers
Answer:
0.75 miles cause 66x60 = 3960 and there are 5280 feet in a mile so 3960 divided by 5280= 0.75
Step-by-step explanation:
How to create the equation of an exponential function given two points
Answers
The final equation will be in the form: y =\(ab^x,\) where 'a' and 'b' are the values you obtained from solving the system of equations.
To create the equation of an exponential function given two points, follow these steps:
Step 1: Identify the two points
Determine the coordinates of the two points on the exponential function. Let's say we have two points: (x₁, y₁) and (x₂, y₂).
Step 2: Set up the exponential function
The general form of an exponential function is y = ab^x, where 'a' is the initial value or y-intercept, 'b' is the base, and 'x' is the independent variable.
Step 3: Set up the system of equations
Substitute the x and y values from the two given points into the exponential function. This will give you two equations:
For the first point (x₁, y₁):
y₁ = \(ab^(x₁)\)
For the second point (x₂, y₂):
y₂ = \(ab^(x₂)\)
Step 4: Solve the system of equations
To solve the system of equations, divide the second equation by the first equation to eliminate 'a':
\(y₂/y₁ = (ab^(x₂))/(ab^(x₁))\)
Simplifying, we get:
\(y₂/y₁ = b^(x₂ - x₁)\)
Take the logarithm of both sides:
\(log(y₂/y₁) = (x₂ - x₁)log(b)\)
Now, you can solve for log(b):
\(log(b) = (log(y₂) - log(y₁))/(x₂ - x₁)\)
Step 5: Find 'b' and 'a'
Using the value of log(b) obtained from the previous step, substitute it back into the equation log(b) = (\(log(y₂) - log(y₁))/(x₂ - x₁\)) to solve for 'b'.
Once 'b' is found, substitute it into one of the original equations (e.g., y₁ = \(ab^(x₁))\) and solve for 'a'.
Step 6: Write the equation of the exponential function
After finding the values of 'a' and 'b', substitute them back into the general form of the exponential function (y = ab^x) to obtain the specific equation.
The final equation will be in the form: y = ab^x, where 'a' and 'b' are the values you obtained from solving the system of equations.
By following these steps, you can create the equation of an exponential function that passes through the given two points.
for more such question on equation visit
https://brainly.com/question/17145398
#SPJ8
If f( x ) = 2 x - 9, then f(3) = -3.
True or False
Answers
Answer:
True
Step-by-step explanation:
f(x)= 2x - 9
f(3) = 2 X 3 -9
f(3)=6-9
=-3
Answer:
true
Step-by-step explanation:
Evaluate f(3), then set it equal to −3
Saeed rented a truck for one day. There was a base fee of $18.95, and there was an additional charge of 78 cents for each kilometer driven. Saeed had to pay $130.49 when he returned the truck. For how many kilometers did he drive the truck?
Answers
Base fee to drive a truck = $18.95
Money payed by Saeed at the end of his drive = $130.49
Money he had to pay for the distance he drove :-
\( = 130.49 - 18.95\)
\( = $111.54\)
Money payed by Saeed for the distance he drove = $111.54
Money charged for an hour's drive = 78 cents
78 cents = $0.78
Distance Saeed drove :-
\( = \frac{111.54}{0.78} \)
\( \color{orange}= 143 \: km\)
Therefore , Saeed drove the truck for 143 km .
step 2 of 3: what is the adjusted coefficient of determination for this model, r2a? round your answer to four decimal places.
Answers
The adjusted coefficient of determination, R2a, cannot be determined without additional information about the model.
To calculate the adjusted coefficient of determination, R2a, we need additional information about the model. The adjusted R2 value takes into account the number of predictors and the sample size to provide a more accurate measure of the model's goodness of fit. Without knowing the specific model, the number of predictors, and the sample size, it is not possible to calculate the adjusted coefficient of determination.
The adjusted R2 formula is given by:
R2a = 1 - [(1 - R2) * (n - 1) / (n - p - 1)]
Here, R2 represents the coefficient of determination, n represents the sample size, and p represents the number of predictors in the model.
Without these values, it is not feasible to determine the adjusted coefficient of determination.
Question: What is the adjusted coefficient of determination, R2a?
To learn more about “coefficient” refer to the https://brainly.com/question/1038771
#SPJ11
step 1 of 4 : state the null and alternative hypotheses in terms of the expected proportion for each day. write your answer as a fraction or a decimal rounded to six decimal places, if necessary.
Answers
By using the concept of testing of hypothesis, the null and alternative hypothesis is given by
\(H_0 :p_i = \frac{1}{5}\)
\(H_a : p_i \neq \frac{1}{5}\) for atleast one day
What is testing of hypothesis?
Suppose there is a hypothesis and there is a data at hand. Testing of Hypothesis determines whether a particular hypothesis is supported by the data at hand.
The null and alternative hypothesis can be written are as follows-
Null hypothesis: \(H_0\) : There is no difference in the number of swimmers from day to day.
Alternative hypothesis: \(H_a\) : There is a difference in the number of swimmers from day to day.
\(H_0 :p_i = \frac{1}{5}\)
\(H_a : p_i \neq \frac{1}{5}\) for atleast one day
To learn more about testing of hypothesis, refer to the link-
https://brainly.com/question/15980493
#SPJ4
Complete Question
The manager of the city pool has scheduled extra lifeguards to be on staff for Saturdays. However, he suspects that Fridays may be more popular than the other weekdays as well. If so, he will hire extra lifeguards for Fridays, too. In order to test his theory that the daily number of swimmers varies on weekdays, he records the number of swimmers each day for the first week of summer. Test the manager’s theory at the 0.10 level of significance.
Swimmers at the City Pool
Monday Tuesday Wednesday Thursday Friday
Number 46 68 43 51 70
Step 1 of 4 :
State the null and alternative hypotheses in terms of the expected proportion for each day. Enter your answer as a fraction or a decimal rounded to six decimal places, if necessary.
H0: pi=⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
Ha: There is a difference in the number of swimmers from day to day.
7th grade math!
Can somebody plz help answer these questions correctly (only if you remmeber how to do this) thx so much :3
WILL MARK BRAINLIEST WHOEVER ANSWERS FIRST :DD

Answers
Answer:
I just learned about this, and if its wrong i am so so sorry
Step-by-step explanation:
a= 120
b= 60
w= 120
x= 120
r= 105
q= 105
p= 105
Answer:
a= 120
b= 60
w= 120
x= 120
r= 75
q= 105
p= 105
Step-by-step explanation:
I need help ! Solve for x.

Answers
The solution for x in the pentagon is 90
How to determine the solution for x?From the question, we have the following parameters that can be used in our computation:
Shape = pentagon
This means that
n = 5
The sum of the internal angles is calculated as
Angles = 180(n - 2)
Substitute the known values in the above equation, so, we have the following representation
Angles = 180(5 - 2)
So, we have
Angles = 540
This means that
x + 90 + 90 + 135 + 135 = 540
So, we have
x + 450 = 540
Evaluate
x = 90
Hence, the value of x is 90
Read more about angles at
https://brainly.com/question/7620723
#SPJ1
i need help with this.. help please?? :,))

Answers
Answer:
C: adding on the right and subtracting on the left; n = 4S: dividing on the left and subtracting on the right; y = 2J: multiplying on the left and dividing on the right; b = 512Step-by-step explanation:
You want the solutions to three equations, and the error in the work shown.
Cullen: -6n +22 = -4n +14Seraphina: 8.4y -6.8 = -3.2y +16.4Jasper: 7/8b -32 = 3/4b +32CullenThe correct solution is ...
\(-6n+22=-4n+14\\\\22=2n+14\qquad\text{add $6n$}\\\\8=2n\qquad\text{subtract 14}\\\\\boxed{4=n}\)
Cullen's error was adding 4n to one side, and subtracting 4n from the other side of the equation. (The same operation must be done to both sides.)
SeraphinaThe correct solution is ...
\(8.4y -6.8 = -3.2y +16.4\\\\11.6y-6.8=16.4\qquad\text{add $3.2y$}\\\\11.6y=23.2\qquad\text{add 6.8}\\\\\boxed{y=2}\)
Seraphina's error was dividing one side of the equation by 11.6 and subtracting 11.6 from the other side. (The same operation must be done to both sides.)
JasperThe correct solution is ...
\(\dfrac{7}{8}b -32 = \dfrac{3}{4}b +32\\\\\dfrac{1}{8}b-32=32\qquad\text{subtract $\dfrac{3}{4}b$}\\\\\dfrac{1}{8}b=64\qquad\text{add 32}\\\\\boxed{b=512}\qquad\text{multiply by 8}\)
Jasper's error was multiplying one side of the equation by 8 and dividing the other side by 8. (The same operation must be done to both sides.)
There is a guitar that originally costs $249.99. It is on sale for 15% off. You also have to pay 6% sales tax. How much will you pay for the guitar? Please show work!!!
Answers
Answer:
225.24099
Step-by-step explanation:
249.99(0.15) = 37.4985
249.99 - 37.4985 = 212.4915
212.4915(0.06) = 12.74949
212.4915 + 12.74949 = 225.24099
Given √2 = 1.414, find the value of (3+ √2)/(3- √2).
Answers
The value of (3 + √2)/(3 - √2) is approximately 11/7 + (6√2)/7.
To find the value of (3 + √2)/(3 - √2), we can use a technique called rationalizing the denominator.
Let's multiply the numerator and denominator of the expression by the conjugate of the denominator, which is (3 + √2):
(3 + √2)/(3 - √2) × (3 + √2)/(3 + √2)
Expanding the numerator and denominator:
[(3 × 3) + (3 × √2) + (√2 × 3) + (√2 × √2)] / [(3 × 3) + (3 × √2) - (√2 × 3) - (√2 × √2)]
Simplifying further:
[9 + 3√2 + 3√2 + 2] / [9 + 3√2 - 3√2 - 2]
Combining like terms:
[11 + 6√2] / [7]
Dividing each term by 7:
11/7 + (6√2)/7
For similar questions on value
https://brainly.com/question/27944341
#SPJ8
EXAMPLE 3.3 What is the chance of getting either 1, 2, 3, 4, 5, or 6 on the next roll? 100%. The outcome must be one of these numbers.
Answers
The chance of getting either 1, 2, 3, 4, 5, or 6 on the next roll of a standard six-sided die is 100%. The outcome must be one of these numbers, as these are the only possible outcomes on a standard six-sided die.
A standard six-sided die has six faces, numbered from 1 to 6. Each face has an equal chance of landing face-up when the die is rolled, assuming the die is fair and not biased. Therefore, the probability of getting any one of the six numbers (1, 2, 3, 4, 5, or 6) on the next roll is 1 out of 6, or 1/6, which is equivalent to approximately 0.1667 or 16.67%. Since there are no other possible outcomes on a standard six-sided die other than these six numbers, the chance of getting either 1, 2, 3, 4, 5, or 6 on the next roll is 100%.
Therefore, the answer is: The chance of getting either 1, 2, 3, 4, 5, or 6 on the next roll is 100% as these are the only possible outcomes on a standard six-sided die.
To learn more about outcome here:
brainly.com/question/27292589#
#SPJ11
PLEASE HELP
Mia I had to create a scale drawing of a football field that is 120 yards by 53 1/3 yards
Explain how she could use a scale of 1: 1,000
Answers
Mia can create a scale drawing of a football field using a scale of 1:1,000. The scale drawing will provide a Visual representation of the field, allowing for easier analysis and planning.
To create a scale drawing of a football field using a scale of 1:1,000, Mia can follow these steps:
1. Determine the dimensions: The football field's dimensions are given as 120 yards by 53 1/3 yards. Convert the fractional measurement to a decimal for simplicity. In this case, 1/3 yard is approximately 0.333 yards.
2. Decide on the units: Since the scale is 1:1,000, Mia needs to determine the unit of measurement she will use in her scale drawing. For consistency, she can choose to use feet as the unit.
3. Calculate the scaled dimensions: To create the scale drawing, Mia needs to scale down the dimensions of the football field. Since the scale is 1:1,000, she can divide the actual dimensions by 1,000 to obtain the scaled dimensions. The scaled dimensions would be 120 yards / 1,000 = 0.12 yards (or 0.36 feet) for the length and 53.333 yards / 1,000 = 0.053333 yards (or 0.16 feet) for the width.
4. Draw the scaled football field: Using a ruler and a grid paper, Mia can draw a rectangle with dimensions of 0.12 feet by 0.053333 feet (or inches, depending on the size of the grid paper). She can label the sides of the rectangle with the corresponding measurements in feet.
5. Add additional markings: Mia can add other markings to the scale drawing, such as the goal posts, yard markers, and any other important features of the football field. She can refer to the actual measurements and proportions of these elements to ensure accuracy.
By following these steps, Mia can create a scale drawing of a football field using a scale of 1:1,000. The scale drawing will provide a visual representation of the field, allowing for easier analysis and planning.
For more questions on Visual .
https://brainly.com/question/28028820
#SPJ8
Here is a data set (n = 117) that has been sorted. 58.5 59.4 60.5 62.1 65.9 65.9 66.2 66.3 66.5 67.4 67.8 68 68.1 68.2 68.2 68.7 69.3 69. 469. 469.8 70. 270.5 70. 771.2 71.5 71.6 71. 9 72. 1 72.6 72.8 73.1 73.4 74.6 | 74.8 74.9 74.9 74.9 75 75.4 75.4 76. 2 76. 4 76. 5 76. 7 76.8 76.9 77.1 . 77.2 77.7 77.9 78 78. 1 78. 2 78. 9 79.4 79.5 79. 8 79.9 80.2 80.5 80. 6 80.7 81.2 81.5 81.7 81. 8 81.8 82.4 82.6 83.183. 1 83.5 83.9 83.9 84.1 | 84.2 84.3 84.3 84.6 85.2 85.6 86 86.1 | 86.1 86.5 86. 6 86. 7 87.1 87.8 88.6 89.1 90. 2 90. 6 90.7 91.4 922 93 93.3 93. 3 94.1 94. 3 95.3 95.5 | 96.1 66.4 69 71.4 74.5 76.2 77.4 79.5 81.6 83.5 85.3 87.3 92.7 101.8 Find the 33rd-Percentile: P. = Preview
Answers
The 33rd percentile is 75.4.
Percentile is defined as the value below which a given percentage falls under. The percentile formula is used when we need to compare the exact values or numbers over the other numbers from the given data i.e. the accuracy of the number.
To find the percentile, here are a few steps to use the percentile formula. If q is any number between zero and hundred, the qth percentile is a value that divides the data into two parts i.e the lowest part contains the q percent of the data and the rest of the data is the upper part.
We find the rank.
Rank = Percentile ÷ 100
Rank = 33 ÷ 100 = 0.33
So, the rank is 0.33.
Using the percentile formula,
Percentile = Rank × Total number of the data set
Percentile = 0.33 × 117
Percentile = 38.61 ≅ 39
Now, counting 39 values from left to right we reach 75.4, and we can say that all the values below 75.4 will come under the 33rd percentile. In other words, 33% of the values are below 75.4.
Therefore, the 33rd percentile is 75.4.
To learn more about percentile, visit: brainly.com/question/1594020
#SPJ4
Frank walked 2400 meters at a rate of 96 meters per minute. If he started walking at 6:45 a.m. and did not take any breaks, at what time did he finish his walk? A. 7:25 a.m. B. 7:20 a.m C. 7:15 a.m. D, 7:10 a.m.
Answers
Since he walks 96 meters per minute Frank will take 2400/96=25 minutes to complete the walk, then he will end by 7:10 a.m
ANSWER FAST WITH WORK
p2+7p divided by 3 for p=5
Answers
Answer:
20
Step-by-step explanation:
I must assume that you meant
p^2 + 7p
---------------
3
If p = 5, then this expression becomes:
5^2 + 7(5) 25 + 35
------------------ = -------------- = 60/3 = 20
3 3
write three equations of lines with a positive slope
Answers
Based on this data, for every inch in height, the arm span increases by 1.1 inches.
Here, we have,
I put the height of people on the x-axis because this is what I am trying to correlate the arm span to. I put the arm span on the y-axis because it is dependent on height.
I used point (60,61) and (70,72) to draw the line of best fit and to get the equation. First, to get the slope I would use the slope formula of m = 72-61/70-60 or 11/10 to get a slope of approximately 1.1. Then I used (60,61) to get the rest of the equation by plugging it in: y-61 = 1.1(x -60). This becomes y-61 = 1.1x - 66. Add 61 to both sides and the final equation is y = 1.1x – 5.
The slope represents the rate of change arm span based on height. The y intercept is the arm span.
Using points (66,68) and points (70,72) I plug each into the equation y=1.1x-5 to figure each out based on the difference from the actual points and get .4 for (66,68) and 0 for point (70,72) so I would say, based on .4 and 0 for these two points that this is a good line of best fit.
Based on this data, for every inch in height, the arm span increases by 1.1 inches.
Learn more about scatterplot on:
brainly.com/question/6592115
#SPJ1
complete question:
There are many measurements of the human body that are positively correlated. For example, the length of one's forearm (measured from elbow to wrist) is approximately the same length as the foot (measured from heel to toe). They are positively correlated because, as one measurement increases, so does the other measurement.
Please help this is timed!!

Answers
Answer:
can i see the rest of the problem...
Step-by-step explanation:
The volume of a cube is given by V = x3 , where x is the length of an edge of the cube. The area of a square is given by A = x2 , where x is the length of a side of the square. A given cube has a volume of 1728 cubic inches.
**Explain how the information given can be used to calculate the surface area of the cube. Use specific details and domain specific vocabulary to construct a coherent response.**
Answers
Answer:
65
Step-by-step explanation:
A presidential candidate plans to begin her campaign by visiting the capitals in 3 of 47 states. What is the probability that she selects the route of three specific capitals? P(she selects the route of three specific capitals) 97290 (Type an integer or a simplified fraction:)
Answers
The probability that she selects the route of three specific capitals is 97290/1.
The probability that she selects the route of three specific capitals can be calculated by taking the total number of possible routes and dividing it by the total number of routes that involve the three specific capitals. To calculate the total number of possible routes, multiply the number of states (47) by the number of routes that could be selected from each state (2). This gives 94 total possible routes.
47 x 46 x 45 ways = 97290 ways
= 1/97290
Now, calculate the number of routes that involve the three specific capitals. Since the president is selecting three states, the total number of routes will be 3. Therefore, the probability that she selects the route of three specific capitals is 3/94, which can be simplified to 97290/1.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
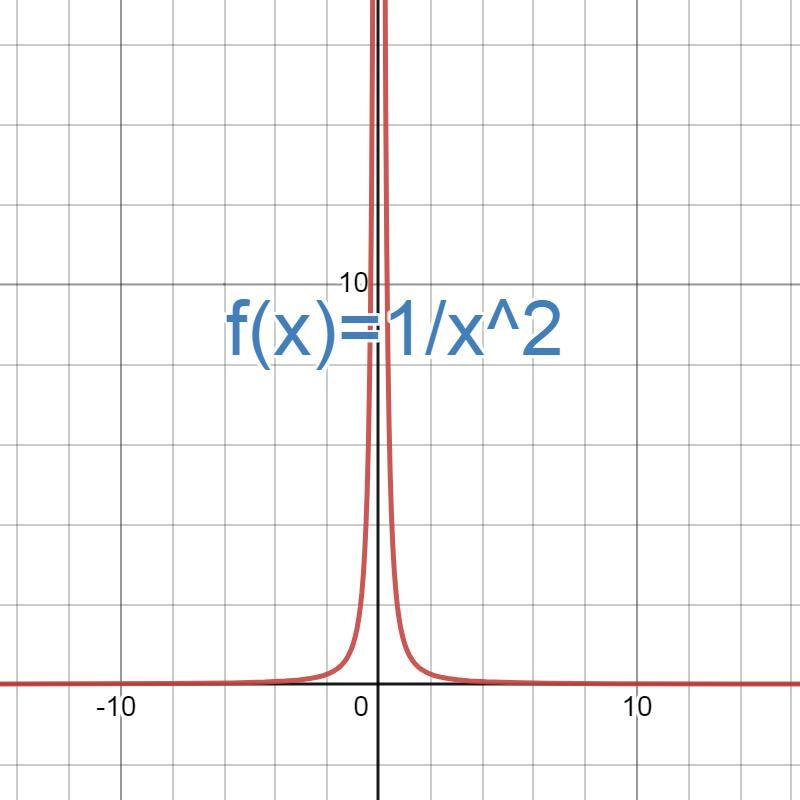
Which of the following rational functions is graphed below?

Answers
Answer: A.
Step-by-step explanation:
1. The function is even (symmetric about the y-axis)
2. The function F(x) is positive
\(\displaystyle\\Hence,\\F(x)=\frac{1}{x^2}\)
Can somebody please help me?
Thank you! :)

Answers
Answer:
Step-by-step explanation:

For the following vectors a = [4,8,8], v = [1,1,0] calculate projection of the vector a in the direction of the vector v a = (**) v = [(a) )x, (a )y, (a )z] av VV a = a, +a mi = a - a a = a ū = TS3 0 VU Find magnitude of the vector a. al = [6,6,0) Submit the Answer 2 Question 2 grade: 0
Answers
The magnitude of vector a is 6√2.
To calculate the projection of vector a onto vector v, we can use the formula:
proj_v(a) = (a · v) / ||v||² × v
where · represents the dot product and ||v|| represents the magnitude of vector v.
Given:
a = [4, 8, 8]
v = [1, 1, 0]
First, let's calculate the dot product (a · v):
(a · v) = 41 + 81 + 8×0 = 4 + 8 + 0 = 12
Next, let's calculate the magnitude of vector v:
||v|| = √(1² + 1² + 0²) = √(2)
Now, we can calculate the projection of vector a onto v:
= 12 / ((√2)² × [1, 1, 0]
= 12 / 2 x [1, 1, 0]
= 6 [1, 1, 0]
= [6, 6, 0]
The projection of vector a onto v is [6, 6, 0].
To find the magnitude of vector a, we can use the formula:
||a|| = √a1² + a2² + a3²
||a|| = √ 6² + 6² + 0²
= √ 36+36
= √72
= 6√2
Thus, The magnitude of vector a is 6√2.
Learn more about Vector here:
https://brainly.com/question/30958460
#SPJ1
For all three of these matrices, follow steps A1 = [2 1 1]
[1 2 0]
[2 2 2]
A2=
[0 1 1]
[2 -1 1]
[2 -2 -1]
A3 =
[-2 -5 -4 -3]
[0 -4 0 0]
[0 0 0 0]
[0 -3 0 2]
a. Calculate the characteristic polynomial by hand.
b. Find the eigenvalues of the matrix A; using matlab or octave's roots() function. Then find the matrix P such that A; = PDP-¹ by hand. c. Use the matrix P to compute by hand the diagonal matrix D = P¹A;P and verify that the elements along the diagonal are indeed the eigenvalues of the matrix A₁.
Answers
a. The characteristic polynomial of matrix A1 is determined by setting det(A1 - λI) = 0, where λ represents an eigenvalue. b. Using MATLAB or Octave's roots() function, we find the eigenvalues of matrix A1. We then obtain the matrix P such that A1 = PDP^(-1), where D is a diagonal matrix consisting of the eigenvalues. c. By computing D = P^(-1)A1P using the matrix P, we can verify that the elements along the diagonal of D are indeed the eigenvalues of matrix A1.
a. To calculate the characteristic polynomial of a matrix, we need to find the eigenvalues. The characteristic polynomial is obtained by setting the determinant of the matrix minus lambda times the identity matrix equal to zero, where lambda represents an eigenvalue. For matrix A1, the characteristic polynomial is obtained by solving the equation det(A1 - lambda*I) = 0.
b. To find the eigenvalues of matrix A1, we can use MATLAB or Octave's roots() function, which calculates the roots of a polynomial. By calculating the eigenvalues, we can find the matrix P such that A1 = PDP^(-1), where D is a diagonal matrix consisting of the eigenvalues of A1.
c. Using the matrix P, we can compute the diagonal matrix D = P^(-1)A1P. This diagonal matrix will have the eigenvalues of matrix A1 along its diagonal. By verifying that the elements along the diagonal of D match the eigenvalues obtained in step b, we can confirm that the computation is correct.
In summary, to solve the problem, we need to calculate the characteristic polynomial of matrix A1, find the eigenvalues using MATLAB or Octave, obtain the matrix P such that A1 = PDP^(-1), and finally compute the diagonal matrix D = P^(-1)A1P. This process confirms that the elements along the diagonal of D are indeed the eigenvalues of matrix A1.
Learn more about matrix here: https://brainly.com/question/29132693
#SPJ11
2 Use a five-variable Karnaugh map to find the minimized SOP expression for the following logic function: F(A,B,C,D,E) = 2m(4,5,6,7,9,11,13,15,16,18,27,28,31)
Answers
The minimized SOP expression for F(A,B,C,D,E) using a five-variable Karnaugh map is D'E' + BCE'. A five-variable Karnaugh map is a graphical tool used to simplify Boolean expressions.
The map consists of a grid with input variables A, B, C, D, and E as the column and row headings. The cell entries in the map correspond to the output values of the logic function for the respective input combinations.
To find the minimized SOP expression, we start by marking the cells in the Karnaugh map corresponding to the minterms given in the function: 2m(4,5,6,7,9,11,13,15,16,18,27,28,31). These cells are identified by their binary representations.
Next, we look for adjacent marked cells in groups of 1s, 2s, 4s, and 8s. These groups represent terms that can be combined to form a simplified expression. In this case, we find a group of 1s in the map that corresponds to the term D'E' and a group of 2s that corresponds to the term BCE'. Combining these groups, we obtain the expression D'E' + BCE'.
The final step is to check for any remaining cells that are not covered by the combined terms. In this case, there are no remaining cells. Therefore, the minimized SOP expression for the given logic function F(A,B,C,D,E) is D'E' + BCE'.
Learn more about combinations here: https://brainly.com/question/29595163
#SPJ11
6- Karen is making a frame for a square picture with an area of 169 square inches. How
many inches of framing are needed?
a) 13
b) 14
c) 15
d) 16
PLEASE HURRY! I WILL MARK YOU BRAINLIST OR WHATEVER... IF YOU DO IT PLEASE
Answers
Answer: a
Step-by-step explanation:
Tell me if it is correct