what 3D shape will be formed when the following shaoes are rotated around the y-axis
Answers
a) If we rotated around the y-axis the triangle we will obtain a cone as a 3d shape.
b) If we rotated around the y-axis the rectangle we will obtain a cylinder as a 3d shape.
c) If we ratated around the y -axis the circle we will obtain as 3d shape an sphere.
Related Questions
The factor tree below provides the factors of 18.
18
N.
2
9
3
3
What is the prime factorization of 18?
2 x 3
2 x 9
2 x 3x3
02x3x9
Answers
Answer: it is (c)
i hope this helped :)
Find x when f (x)= 25
Answers
Some entrepreneurs wish to establish a restaurant in a central location so that it will serve three suburbs. On a rectangular grid with axes labelled X1 (horizontal) and X2 (vertical), the centres of the three suburbs are located at (1,2, (6,18), and (12,8). All roads run east-west (parallel with the X1 axis) or north-south (parallel with the X2 axis). The distance between any two points is therefore rectilinear. For example, the distance between the centres of suburbs 2 and 3 is |12- 6| + | 8-18|= 6 +10 =16.
Required:
a. Formulate the restaurant location problem as a goal programming model.
b. Use the Excel Solver to determine the best location for the restaurant.
Answers
What is the 95% confidence interval for this population proportion? Answer choices are rounded to the hundredths place.
0.11 to 0.21
0.10 to 0.23
0.16 to 0.17
0.11 to 0.16
Answers
The 95% confidence interval for this population proportion is (0.10,0.23).
sample size n = 125
number of people planned to take an extended vacation = 21
sample proportion (p) = 21/125 = 0.168
Confidence level = 0.95
significance level (α) = 1-0.95 = 0.05
Z score = Z(0.05) = 1.96, from the Z table.
confidence interval for a population proportion is-
p±Zα/2 *\(\sqrt{\frac{p(1-p)}{n} }\) = 0.168± 1.96\(* \sqrt{\frac{0.168(1-0.168)}{125} }\)
= 0.168 ± 1.96*0.334
= 0.168 ± 0.0655
= (0.1025, 0.2335)
= (0.10,0.23)
Hence, the confidence interval is (0.10,0.23).
Read more about the confidence interval:
https://brainly.com/question/15712887
#SPJ4
The average spending at Neco's salad bar is $8.73 with a standard deviation of $3.41. The distribution follows t-distribution. The management is interested in the middle 90% of the customers (spending wise) as it believes that they represent their true customer base. What will be the difference between the upper and lower spending cut-offs which define the middle 90% of the customers if the sample contains 41 customers
Answers
Answer:
Difference between upper and lower limits is : 1,816
Step-by-step explanation:
A CI (confidence interval ) for t student distribution is:
( μ₀ - t(α/2)* s/√n ; μ₀ + t(α/2)* s/√n )
Where:
μ₀ is the mean and s the standard deviation of the dstribution
n size of the sample
CI = 90 % means α = 10 % α = 0,1 α/2 = 0,05
and degree of freedom df = n - 1 df = 40
From t student table we get:
tα/2 = 1,6839
Then:
t(α/2)* s/√n = 1,6839* 3,41/√40
t(α/2)* s/√n = 0,908
8,73 - 0,908 = 7,822
8,73 + 0,908 = 9,638
CI (90%) = ( 7,822 ; 9,638 )
Difference between upper and lower cut-offs points is:
Δ = 1,816
g a mathematician wishes to prove the following proposition using a proof by induction: the sum of the first n consecutive odd numbers equals n2. which of the following can be used as part of the inductive step in her proof?
Answers
the inductive step in her proof 1+2+3+…+k+(2k+1)=k2+(2k+1)=> 1+2+3+…+k+(2k+1)=(k+1)2…
a mathematician wishes to prove the following proposition using a proof by induction: the sum of the first n consecutive odd numbers equals n2. the following can be used as part of the inductive step in her proof:
We have:
1=12
true
1+3=4=22
true
1+3+5=9=32
true
We assume that for n=k
:
1+3+5+…+2k−1=k2…(1)
We will show that for n=k+1
:
1+3+5+…+2k−1+2(k+1)−1=(k+1)2=>
1+3+5+…+2k−1+2k+1=(k+1)2…(2)
We now add the term 2k+1
to both sides of (1)
and we take:
1+2+3+…+k+(2k+1)=k2+(2k+1)=>
1+2+3+…+k+(2k+1)=(k+1)2…(3)
Learn more about induction from brainly, visit: brainly.com/question/13540448
#SPJ4
Find the following measure for this figure.
Volume =

Answers
Answer:
91 2/3 pi cubic units
Step-by-step explanation:
The formula for the volume of cone is \(\dfrac{1}{3}\pi r^2 h\). Plugging in the given numbers, you get:
\(\dfrac{1}{3}\cdot \pi \cdot 5^2 \cdot 11= 91 \ 2/3 \pi\)
Hope this helps!
Answer:
\(Volume=\frac{1}{3} \,275\,\pi\) cubic units
Notice that this answer doesn't agree with any of the first three in the list provided via the screenshot
Step-by-step explanation:
Recall the formula for the volume of a cone:
\(Volume=\frac{1}{3} Base\,*\,Height\)
In this case the Height is 11 units, and they also give us the radius of the circular base (5 units) from which we can find the circle's base area:
\(Area_{circle} = \pi\,R^2\\Area_{circle}=\pi\,(5)^2\\Area_{circle}=25 \pi\)
therefore the total volume becomes:
\(Volume=\frac{1}{3} Base\,*\,Height\\Volume=\frac{1}{3} 25\,\pi\,*\,11\\\\Volume=\frac{1}{3} \,275\,\pi\)
at which points do the graphs of y= x+1 and y=2^2 intersection
Answers
The graphs of y = x + 1 and y = 2^x intersect at approximately (-0.3517, 0.6483) and (1.561, 3.561).
To find the points of intersection between the graphs of y = x + 1 and y = 2^x, we need to set the two equations equal to each other and solve for x.
Setting y = x + 1 equal to y = 2^x, we have:
x + 1 = 2^x
To solve this equation, we can use numerical methods or make observations to find the points of intersection. By observing the behavior of the two functions, we can see that they intersect at two points: one when x is negative, and another when x is positive.
For x < 0, the exponential function y = 2^x approaches 0 as x approaches negative infinity, while the linear function y = x + 1 continues to decrease as x becomes more negative. Thus, there is one point of intersection in this region.
For x > 0, the exponential function grows faster than the linear function, so there is another point of intersection in this region.
However, finding the exact values for the points of intersection requires numerical methods such as using a graphing calculator or solving the equation numerically. Approximate values for the points of intersection can be found as x ≈ -0.3517 and x ≈ 1.561.
for more such questions on graphs
https://brainly.com/question/29538026
#SPJ8
each function
f(x)=-4x-5;
ion for
Find ƒ(1)
for the given
Answers
When x is equal to 1, the Function f(x) = -4x - 5 yields a value of -9.
The find ƒ(1) for the function f(x) = -4x - 5, we need to substitute x = 1 into the function and evaluate the expression.
Replacing x with 1, we have:
ƒ(1) = -4(1) - 5
Simplifying further:
ƒ(1) = -4 - 5
ƒ(1) = -9
Therefore, when x is equal to 1, the value of the function f(x) = -4x - 5 is ƒ(1) = -9.
Let's break down the steps taken to arrive at the solution:
1. Start with the function f(x) = -4x - 5.
2. Replace x with 1 in the function.
3. Evaluate the expression by performing the necessary operations.
4. Simplify the expression to obtain the final result.
In this case, substituting x = 1 into the function f(x) = -4x - 5 gives us ƒ(1) = -9 as the output.
It is essential to note that the notation ƒ(1) represents the value of the function ƒ(x) when x is equal to 1. It signifies evaluating the function at a specific input value, which, in this case, is 1.
Thus, when x is equal to 1, the function f(x) = -4x - 5 yields a value of -9.
For more questions on Function .
https://brainly.com/question/11624077
#SPJ8
Pls help I’ll mark brainliest!!

Answers
Answer:
Answer is explained in the photo

Hi! I need the area of this figure! Please Help! Worth 20 points!

Answers
Answer:
A = (18π +72) cm²P = (12π +12) cmStep-by-step explanation:
areaThe area of a semicircle is ...
A = 1/2(πr²)
For a radius of 6 cm, the (top) semicircle area is ...
A = (1/2)π(6 cm)² = 18π cm²
__
We notice that the area of the bottom-most semicircle exactly fills the empty space next to it. That is, the area of the bottom part of the figure is exactly the area of 2 squares of side length 6 cm.
rectangle area = 2(6 cm)² = 72 cm²
Then the total area of the figure is ...
(72 +18π) cm²
__
perimeterThe perimeter of a semicircle of radius r is ...
P = 1/2(2πr) = πr
So, the length of arc AE is ...
AE = π(6 cm) = 6π cm
The two semicircles at the bottom of the figure have a total arc length exactly equal to the circumference of a circle 6 cm in diameter. That is ...
C = πd
C = π(6 cm) = 6π cm
The two straight sides of the figure have a total length equal to twice the side length of each square:
P = 2s = 2(6 cm) = 12 cm
Then the perimeter of the figure is ...
AE +(AB+DE) +BCD
= 6π cm + 12 cm + 6π cm
= (12 +12π) cm
_____
Additional comment
Usually, "completely simplified" means that parentheses are eliminated from the expression and like terms are combined. While the perimeter expression shown in the problem statement is numerically correct, it does not qualify as being "completely simplified". (You may prefer to write the π-term first. Often the answer checker will choke on parentheses, and it may prefer the value have no spaces. YMMV)
2. Suppose the price of good x increased from 4 birr to 5 birr. Because of change price of good x, quantity demand of good y changed from 5,000 to 6,250. a. Find cross price elasticity of demand b. What types of goods (good x and good y) are?
Answers
Based on the cross-price elasticity of Demand, we can conclude that good X and good Y are substitutes.
Let's calculate the cross-price elasticity of demand using the given information:
a. Find the percentage change in quantity demanded of good Y:
Percentage Change in Quantity Demanded of Good Y = (New Quantity Demanded - Initial Quantity Demanded) / Initial Quantity Demanded * 100
Percentage Change in Quantity Demanded of Good Y = (6250 - 5000) / 5000 * 100 = 25%
b. Find the percentage change in the price of good X:
Percentage Change in Price of Good X = (New Price - Initial Price) / Initial Price * 100
Percentage Change in Price of Good X = (5 - 4) / 4 * 100 = 25%
Now, we can calculate the cross-price elasticity of demand:
Cross-Price Elasticity of Demand = Percentage Change in Quantity Demanded of Good Y / Percentage Change in Price of Good X
Cross-Price Elasticity of Demand = 25% / 25% = 1
b. Based on the calculated cross-price elasticity of demand, we can determine the types of goods:
If the cross-price elasticity of demand is positive (as in this case, where it is 1), it indicates that the two goods are substitutes. This means that when the price of good X increases, the quantity demanded of good Y also increases, suggesting that consumers view these goods as alternatives to each other.
Therefore, based on the cross-price elasticity of demand, we can conclude that good X and good Y are substitutes.
For more questions on Demand.
https://brainly.com/question/14274996
#SPJ8
Answer:
Step-by-step explanation:
Use a calculator to graph f(x) = 2x ^ 3 - 6x ^ 2 - 4x + 1 Which are the approximate x-values of the local maximum and local minimum rounded to the nearest tenth?
A) max ≈ -15.6 , min ≈ 1.6
B) max ≈ 1.6 , min ≈ -15.6
C) max ≈ 2.3 , min ≈ -0.3
D) max ≈ -0.3 , min ≈ 2.3
Answers
The approximate x-values for the local maximum and the local minimum are given as follows:
D) max ≈ -0.3 , min ≈ 2.3.
What are the relative minimums and the relative maximums of a function?The relative minimums of a function are given by the points in which the function's behavior changes from decreasing to increasing.The relative maximums of a function, meanwhile, are given by the points in which the function's behavior changes from increasing to decreasing.Hence the critical points of the graphed function are given as follows:
Maximum: x = -0.3.Minimum: x = 2.3.More can be learned about relative minimums of a function at https://brainly.com/question/9839310
#SPJ1

For the question of total area of the cuboid is 200cm^.
I understand where we divide 150 by 4.
But why do I need to multiply by 5, when there are 6 faces.
Answers
You need to multiply by 5 instead of 6 because each pair of opposite faces on a cuboid has the same area, so by considering one face from each pair, you ensure that you don't count any face twice.
When calculating the total surface area of a cuboid, you need to understand the concept of face pairs.
A cuboid has six faces, but each face has a pair that is identical in size and shape.
Let's break down the reasoning behind multiplying by 5 instead of 6 in the given scenario.
To find the surface area of a cuboid, you can add up the areas of all its faces.
However, each pair of opposite faces has the same area, so you avoid double-counting by only considering one face from each pair. In this case, you have five pairs of faces:
(1) top and bottom, (2) front and back, (3) left and right, (4) left and back, and (5) right and front.
By multiplying the average area of a pair of faces by 5, you account for all the distinct face pairs.
Essentially, you are considering one face from each pair and then summing their areas.
Since all the pairs have the same area, multiplying the average area by 5 gives you the total surface area.
When dividing 150 by 4 (to find the average area of a pair of faces), you are essentially finding the area of a single face.
Then, by multiplying this average area by 5, you ensure that you account for all five pairs of faces, providing the total surface area of the cuboid.
Thus, multiplying by 5 is necessary to correctly calculate the total surface area of the cuboid by accounting for the face pairs while avoiding double-counting.
For similar question on cuboid.
https://brainly.com/question/29568631
#SPJ8
Which is the
4
graph of f(x) = 4[*?
-3-2--1₁-
-2-
2 3 4 5 6
4
1
1-2--11-
-2
2 3
56
4
2-11.
-2-
23
56

Answers
Option 2 is the correct graph for the function f(x) = \(4[(1/2)^{x}]\) .
Given ,
f(x) = \(4[(1/2)^{x}]\)
Mathematically the graph will of exponential in nature.
So,
Let us assume few values to understand the nature of graph.
Firstly,
Let x= 1
f(x) = \(4[(1/2)^{1}]\)
f(x) = 2
Let x = 2
f(x) = \(4[(1/2)^{2}]\)
f(x) = 1
Let x = 3
f(x) = \(4[(1/2)^{3}]\)
f(x) = 0.5
Thus from these values of f(x) corresponding to the values of x second graph will be correct .
Learn more about exponent graph,
https://brainly.com/question/13559671
#SPJ1
The average student at Rio Hondo takes 9.1 units per semester (SD = 1.2). Some people believe that students in transfer level math will be more likely to be on track to graduate quickly. Five students from PSY 190 were taking 12, 14, 6, 6, and 16 units. Conduct the steps of hypothesis testing to determine whether students in PSY 190 take more units compared to the average Rio Hondo student.
Answers
The critical value from the given data is 2.776.
Hypothesis Testing:
Step 1: State the null and alternative hypotheses.
Null Hypothesis (H0): The average number of units taken by students in PSY 190 is equal to the average number of units taken by Rio Hondo students.
Alternative Hypothesis (H1): The average number of units taken by students in PSY 190 is greater than the average number of units taken by Rio Hondo students.
Step 2: Calculate a test statistic.
To calculate a test statistic, we will use a one-sample t-test. The t-test will allow us to compare the average of the PSY 190 students to the average of all Rio Hondo students. The test statistic will be calculated as follows:
t = (x - μ) / (s/√n)
Where x is the sample mean, μ is the population mean, s is the sample standard deviation, and n is the sample size.
In this case, x = 10.6, μ = 9.1, s = 5.1, and n = 5.
Plugging these values into the equation, we get:
t = (10.6 - 9.1) / (5.1/√5) = 1.78
Step 3: Determine the critical value.
To determine the critical value, we need to determine the degrees of freedom, which is equal to n-1 = 4. We can then look up the critical value in a t-table with α = 0.05 and 4 degrees of freedom. The critical value is 2.776.
Step 4: Compare the test statistic to the critical value.
Since the test statistic (1.78) is less than the critical value (2.776), we fail to reject the null hypothesis.
Therefore, the critical value from the given data is 2.776.
Learn more about the critical value here:
https://brainly.com/question/14508634.
#SPJ1
Quiana measures the width of her doorway entrance using a measuring tape.She measures the width as 33 inches. She later finds a better tape measure that measures to the nearest half of an inch. After re-measuring,she determines that the actual measure of the doorway is 32 1/2 inches
Answers
2.
Carla is 5 years old and Jim is 13 years younger than Peter. One year ago, Peter's
age was twice the sum of Carla's and Jim age. How old is each child now?
Answers
Jim = Peter - 13
one year ago peter = one year ago
(carla + Jim) * 2
First put any numbers you can into the third equation
Step-by-step explanation:
enjoyyyyyy brooooooooooooooooo

In the figure, AB =
Inchesand AC=
inches.
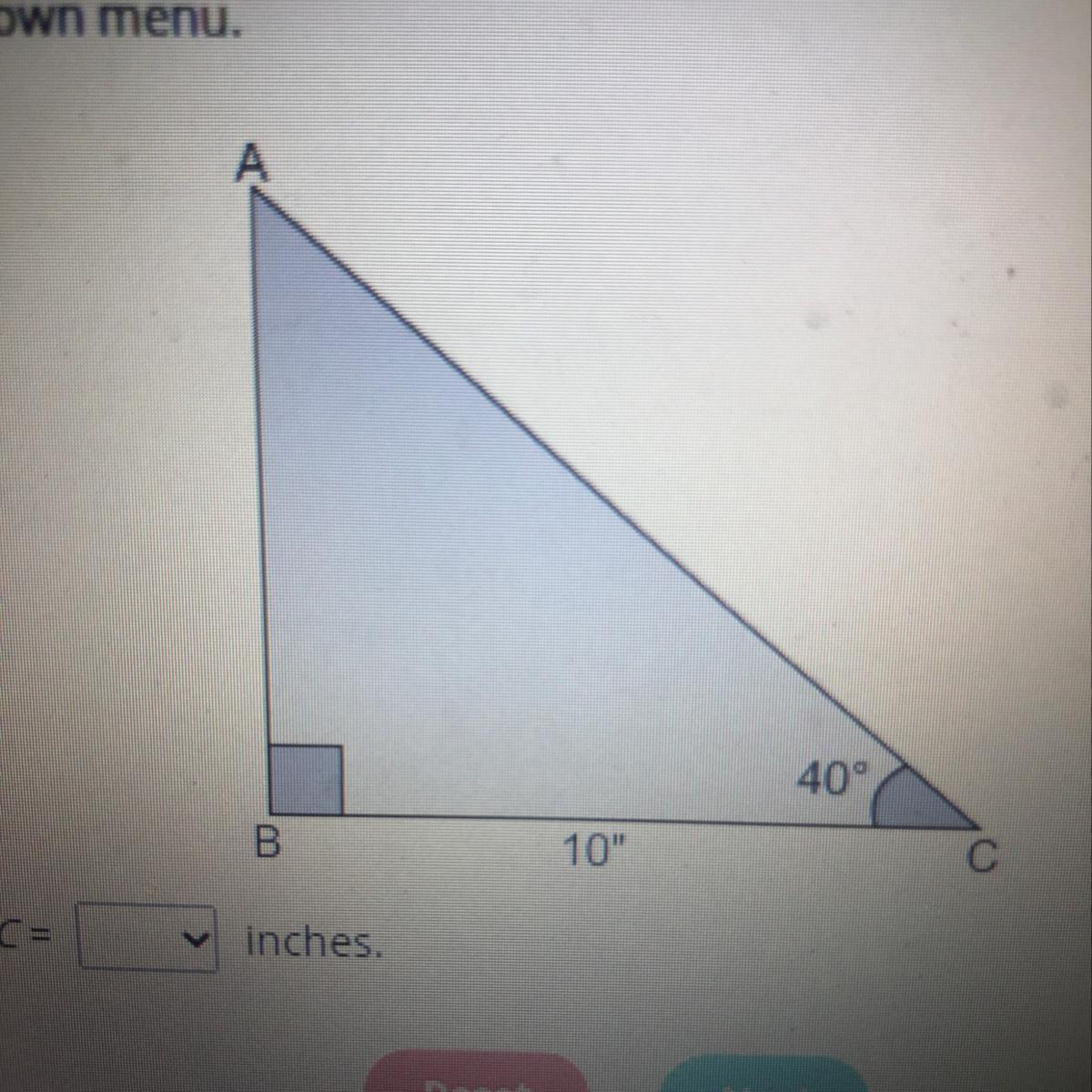
Answers
Answer:
\(\displaystyle AB \approx 8.39 \text{ inches} \text{ and } AC \approx 13.05 \text{ inches}\)
Step-by-step explanation:
Note that we are given the measure of ∠C and the length of side BC.
To find AB, we can use the tangent ratio. Recall that:
\(\displaystyle \tan\theta = \frac{\text{opposite}}{\text{adjacent}}\)
Substitute in appropriate values:
\(\displaystyle \tan 40^\circ = \frac{AB}{BC} = \frac{AB}{10}\)
Solve for AB:
\(\displaystyle AB = 10\tan 40^\circ \approx 8.39\text{ inches}\)
For AC, we can use cosine ratio since we have an adjacent and need to find the hypotenuse. Recall that:
\(\displaystyle \cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}}\)
Substitute in appropriate values:
\(\displaystyle \cos 40^\circ = \frac{BC}{AC} = \frac{10}{AC}\)
Solve for AC:
\(\displaystyle \begin{aligned} \frac{1}{\cos 40^\circ} & = \frac{AC}{10} \\ \\ AC & = 10\cos 40^\circ \approx 13.05\text{ inches} \end{aligned}\)
In conclusion, AB is about 8.39 inches and AC is about 13.03 inches.
I need help on this problem please?

Answers
Answer:
yes ur friend is correct
Step-by-step explanation:
because the value of x .
The diagram only shows that angles M and B are supplementary ( add up to 180 degrees) and that angel 4x is adjacent to angel M.However, there is no information about the measure of angle B or angel M, so we cannot determine the value of x
Which of these graphs shows line CD parallel to line MP and passing through point (1, -3)

Answers
A. y = -1
B. X = -1
C. y = 1
D. X = 1

Answers
The highest point in the number is X=1
Can someone help me with this problem

Answers
Answer:
c (88)
Step-by-step explanation:
find angle opposite to the arc BC
A=2 (92)=184
A=360-184
A=176
D=2÷A
D=2÷176
D=88
Find the missing side or angle. Round to the nearest tenth. C=53° B= 80° a=2 b=[ ? ]
Answers
9514 1404 393
Answer:
b ≈ 2.7
Step-by-step explanation:
The missing angle A is ...
A = 180° -53° -80° = 47°
The law of sines tells you ...
b/sin(B) = a/sin(A)
b = sin(80°)×2/sin(47°) ≈ 2.6931
Side b is about 2.7 units.
![Find the missing side or angle. Round to the nearest tenth. C=53 B= 80 a=2 b=[ ? ]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/uuZUY9piAAZ3A4LEyPYPXAKj1UL7YXNS.png)
Answer:
b~ 2.7Step-by-step explanation:
hope it helps much
HELP a movie theater charges $4 for a drink and $6 for pail of popcorn what is the total charge for d drinks and p popcorns
Answers
The total cost for d drinks and p popcorns can be calculated by multiplying the number of drinks by the cost per drink ($4) and adding it to the number of popcorns multiplied by the cost per popcorn ($6), like this:
Total cost = (cost per drink x number of drinks) + (cost per popcorn x number of popcorns)
Total cost = ($4 x d) + ($6 x p)
So the answer would be:
Total cost = $4d + $6p
The total charge for d drinks is 4d, and the total charge for p popcorns is 6p. Therefore, the total charge for d drinks and p popcorns is:
4d + 6p
A farmer earns $___ for each orange she sells. She had to pay $___ for fertilizer. Part A: Rewrite the description by filling in the blanks with values of your choice to show the amount of money the farmer could earn selling any number of oranges, n. Make sure the values you choose make sense for this situation. (6 points) Part B: Write an algebraic expression from your written description used in Part A. Let n stand for the number of oranges. (6 points)
Answers
Part B: The algebraic expression for the amount of money the farmer could earn selling any number of oranges, n, is 0.20n - 25.
Find x if angle 1 = 2x+10 and angle 2 = 3x-6
Answers
angle 1 + angle 2 = (2x + 10) + (3x - 6) = 5x + 4
Since this sum is equal to 180 degrees, we can write:
5x + 4 = 180
Subtracting 4 from both sides:
5x = 176
Dividing both sides by 5:
x = 35.2
Therefore, x is 35.2 degrees.
An actuary was analyzing the loss experienced by flooding on houses and concluded that it was uniformly distributed on [0, 1000]. After taking another look at the data, he realized the loss amounts used were in real dollars. He then determined that the inflation rate was at 6.5%. Assume that the rest of his analysis still holds true. Calculate the probability that the loss in nominal dollars is less than 1000, given that the loss in nominal dollars is greater than 200.
Answers
Answer:
100% probability that the loss in nominal dollars is less than 1000, given that the loss in nominal dollars is greater than 200.
Step-by-step explanation:
Uniform probability distribution:
An uniform distribution has two bounds, a and b.
The probability of finding a value of at lower than x is:
\(P(X < x) = \frac{x - a}{b - a}\)
The probability of finding a value between c and d is:
\(P(c \leq X \leq d) = \frac{d - c}{b - a}\)
The probability of finding a value above x is:
\(P(X > x) = \frac{b - x}{b - a}\)
Uniformly distributed on [0, 1000].
This means that \(a = 0, b = 1000\)
Given that the loss in nominal dollars is greater than 200.
This means that \(a = 200\)
Calculate the probability that the loss in nominal dollars is less than 1000
\(P(X < x) = \frac{x - a}{b - a}\)
\(P(X < 1000) = \frac{1000 - 200}{1000 - 200} = 1\)
100% probability that the loss in nominal dollars is less than 1000, given that the loss in nominal dollars is greater than 200.
5.3 MATHEMATICS HOLIDAY PACKAGE-TERM 2(2023) Instructions: Attempt ALL items 1. Your family has seven siblings; peter, John, Sarah, Joy, Ali, Mary and Ivan. There is an interval of 2 years between the ages of the children from Ivan to peter. Ivan is three years old. Task: Using an arrow diagram, explain the information about your family.
Answers
describe the effect on the graph of the parent f(x)=x

Answers
we know that
the parent function is
f(x)=x
The line passes throught the origin
the slope is m=1
Find the equation of the line g(x)