Wally Beige has painted a rectangular mural that is 7 ft tall and 11 ft wide. He plans to paint a border of equal width all the way around the outside of the mural. To end up with a border that has an area of 88 square ft, find the width of the border.
Answers
Answer:
Width = 4ft
Step-by-step explanation:
Area of the rectangular mural = Length × Breadth
7 ft tall and 11 ft wide.
(11 - 2W)(7 - 2W) = 88
77 -22W - 14W + 4W² = 88
77 -36W + 4W² = 88
4W² - 36W + 77 - 88
= 4W² - 36W - 11
W = 4ft
Related Questions
Continuously Compounding: A(t)=A(0)x e^rt
3. The amount of a radioactive element in a compound decreases continuously at an hourly rate of 15%. At noon there are 4500 nanograms of the element in the compound. How much of the element will there be at 6 p.m.?
4. A population of seabirds has been growing continuously at a rate of 4% per year. Today, the population is 16,000.
a. What will the population be 6 years from now?
b.What was the population 6 years ago?
Answers
Therefore, the population of seabirds 6 years ago was approximately 11,745.5.
What is percent?Percent is a way of expressing a number as a fraction of 100. It is represented by the symbol "%". For example, if there are 25 students in a class and 20 of them passed the test, the percentage of students who passed the test is 80%. This is calculated by taking the number of students who passed (20) and dividing it by the total number of students (25), then multiplying by 100.
Here,
3. The amount of the radioactive element can be modeled by the equation:
\(A(t) = A(0) *e^{rt}\)
where A(t) is the amount of the element at time t, A(0) is the initial amount at time t=0, r is the continuous rate of decrease, and e is the mathematical constant approximately equal to 2.71828.
In this problem, we know that the initial amount A(0) is 4500 nanograms, the continuous rate of decrease r is 15% per hour, and we want to find the amount of the element at 6 p.m., which is 6 hours after noon.
First, we need to convert the continuous rate of decrease from hourly to continuous, using the formula:
r = ln(1 - p)
where p is the hourly rate of decrease, expressed as a decimal. In this case, p = 0.15, so:
r = ln(1 - 0.15)
≈ -0.1707
Substituting the given values into the equation for A(t), we get:
\(A(t) = 4500*e^{-0.1707t}\)
where t is the time in hours since noon. To find the amount of the element at 6 p.m. (t = 6), we plug in t = 6 and evaluate:
\(A(6) = 4500*e^{-0.1707*6}\)
≈ 2595.5
Therefore, there will be approximately 2595.5 nanograms of the element at 6 p.m.
4a. The population of seabirds can be modeled by the equation:
\(P(t) = P(0)*e^{rt}\)
where P(t) is the population at time t, P(0) is the initial population at time t=0, r is the continuous rate of growth, and e is the mathematical constant approximately equal to 2.71828.
In this problem, we know that the initial population P(0) is 16,000, the continuous rate of growth r is 4% per year, and we want to find the population 6 years from now.
We need to convert the continuous rate of growth from years to continuous, using the formula:
r = ln(1 + p)
where p is the annual rate of growth, expressed as a decimal. In this case, p = 0.04, so:
r = ln(1 + 0.04)
≈ 0.0392
Substituting the given values into the equation for P(t), we get:
\(P(t) = 16000*e^{0.0392t}\)
where t is the time in years since the initial time. To find the population 6 years from now (t = 6), we plug in t = 6 and evaluate:
\(P(6) = 16000*e^{0.0392*6}\)
≈ 20661.7
Therefore, the population of seabirds will be approximately 20,661.7 in 6 years.
4b. To find the population 6 years ago, we can use the same equation but with t = -6 (since we are going back in time):
\(P(6) = 16000*e^{0.0392*-6}\)
≈ 11745.5
To know more about percent,
https://brainly.com/question/29172752
#SPJ1
what is −5/6÷9/10 HELP FAST
Answers
Answer:
the answer to the question is -25/27

Suppose you conducted an experiment with 20 participants in each group. You would have _____ degrees of freedom in an independent-groups design and _____ degrees of freedom in a correlated-groups design.
Answers
You would have 19 degrees of freedom in an independent-groups design and 20 degrees of freedom in a correlated-groups design..
In an independent-groups design, you would have 19 degrees of freedom. This is because the degrees of freedom for an independent-group design is equal to the number of participants minus one. Therefore, in this example, 20 participants minus one equals 19 degrees of freedom.
In a correlated-groups design, you would have 18 degrees of freedom. This is because the degrees of freedom for a correlated-groups design is equal to the number of participants minus two. Therefore, in this example, 20 participants minus two equals 18 degrees of freedom.
For more questions like Degrees of freedom click the link below:
https://brainly.com/question/13149870
#SPJ4
I’m confused on this question.

Answers
Answer:
The second box plot represents the data
Step-by-step explanation:
A box and whisker plot gives you the five-number summary of the data, which includes:
the minimum (lowest value of the data)
the maximum (highest value of the data)
Q1 (25% of the data lies below this point)
Q3 (75% of the data lies below this point), and
the median (the middle of the data).
The two ticks at the far left and far right of the box-and-whisker plot are the minimum and maximum respectively. From the data, we see that the minimum is 5 and the maximum is 10.
Although both plots have a minimum value of 5, only the second plot has the accurate maximum at 10.
How can limit be used in real life
Answers
Answer:
Engineers use limits in real life.
Step-by-step explanation:
Limits are also used as real-life approximations to calculating derivataves. So to make calculations, engineers will approximate a function using small differences in the function and then try and calculate the derivative of the function by having smaller and smaller spacing in the function sample intervals.
The base of a triangle is 3 inches shorter than twice the height. If the area is 10 inches squared,
what is the base and the height?
Answers
Answer:
height = 4 in
base = 5 in
Step-by-step explanation:
The area of a triangle can be found using the equation:
\(A = \frac{1}{2} bh\)
where \(b\) is the base of the triangle and \(h\) is the base.
In order to plug into this equation, we need to use the relationship between the base and height. It is given that the base is 3 inches shorter than twice the height. Converting this to a mathematical equation:
\(b = 2h-3\)
Since we are given that the area is 10 inches squared, we can now plug into the area equation to solve for the height (using the quadratic formula):
\(10 = \frac{1}{2} (2h-3)(h)\\2h^2 - 3h -20 = 0\\h = 4\)
** We reject the negative solution of -5/2, since the triangle's height cannot be negative.
Now, we can simply plug in this height to solve for the base:
\(b = 2(4) - 3\\b = 5\)
Question 6 of 24
The function f(x) = x2 - 6x + 9 is shifted 5 units to the right to create g(x).
What is g(x)?
A. g(x) = (x - 5)2 - 6(x - 5) + 9
B. g(x) = (x + 5)2 - 6(x + 5) + 9
C. g(x) = (x2 - 6x + 9) + 5
D. g(x) = (x2 - 6x + 9) - 5
Micr
SUBMIT
Answers
Answer:
Step-by-step explanation: its b
help
What are the solutions to the following system of equations? y = x2 + 8x + 12 3x + y = −6
Answers
The solutions for the given system of equations are (-9, 33) and(-2, 12).
What is a linear system of equations?A system of linear equations consists of two or more equations made up of two or more variables such that all equations in the system are considered simultaneously. The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently.
The given system of equations are y=x²+8x+12 -----(i) and 3x+y=-6 -----(ii).
Here, y=-6-3x in the equation (i), we get
-6-3x=x²+8x+12
x²+8x+12+6+3x=0
x²+11x+18=0
Splitting middle term method, we get
x²+9x+2x+18=0
x(x+9)+2(x+9)=0
(x+9)(x+2)=0
x=-9 or x=-2
Substitute x=-9 in the equation (ii), we get
y=-6-3(-9)
y=33
Substitute x=-2 in the equation (ii), we get
y=-6-3(-2)
y=12
So, solutions are (-9, 33) and(-2, 12)
Therefore, the solutions for the given system of equations are (-9, 33) and(-2, 12).
To learn more about the linear system of an equations visit:
https://brainly.com/question/27664510.
#SPJ1
The supplement of an angle is 3 times the measure. What is the measure of the angle?
Answers
find the value of the expression -x^3+3 x^2-x+20 if x=-1
Answers
The value of the expression -x³ + 3x² - x + 20 when x = -1 is 23.
What is the value of the given expression when x = -1?Given the expression in the question;
-x³ + 3x² - x + 20
x = -1To determine the value of the expression,
First, we substitute -1 for x in the expression:
-( -1 )³ + 3( -1 )² − ( -1 )) + 20
Next, we simplify each term using the order of operations (also known as PEMDAS):
-( -1 )³ = -( -1 ) = 1
(recall that the exponent is evaluated first, then the negative sign is applied)
3( -1 )² = 3(1) = 3
(recall that the exponent is evaluated first)
-( -1 ) = 1
(recall that subtracting a negative is the same as adding a positive)
Now, putting these simplified terms back into the original expression, we get:
1 + 3 + 1 + 20
Finally, we add these terms together to get the final answer:
23
Therefore, the value of the expression is 23.
Learn about PEMDAS here: https://brainly.com/question/36185
#SPJ1
I need to know the answer and how to solve this

Answers
Explanation
when a line intersect a pair of parallel lines, diverse angles are formed
As we can see, angles 1 and angle 2 are supplementary , ( the sum equal 180)
the same for angles 3 and 4,
also angle1 is congruent to angle 3
\(m\angle1=m\angle3\text{ Eq(1)}\)
and
angle 3 and 4 are supplementary ,so
\(\begin{gathered} m\angle3+m\angle4=180 \\ \text{replace m}\angle4=115 \\ m\angle3+115=180 \\ \text{subtract 115 in both sides} \\ m\angle3+115-115=180-115 \\ m\angle3=65 \\ m\angle3=m\angle1=65 \end{gathered}\)I hope this helps you

Calculate the ratio

Answers
Where the conditions above are given with regard to the above triangle, the ratio AD:DB is 1:1.
What is the explanation for the above response?Since D is the midpoint of AB, we have:
AD = DB
Let M and N be the midpoints of OA and OB, respectively. Then we have:
AM = MO = x/2
BN = NO = y/2
Also, from the given information, we have:
OD = 3/7x + 4/7y
Since D is the midpoint of AB, we have:
AD + DB = AB
Substituting AD = DB, we get:
2AD = AB
Therefore:
AD = AB/2
We can express AB in terms of x and y using the law of cosines:
AB^2 = OA^2 + OB^2 - 2(OA)(OB)cos(BOA)
Since M and N are midpoints, we have:
OM = OA/2 and ON = OB/2
Therefore, using the law of cosines, we have:
MN^2 = OM^2 + ON^2 - 2(OM)(ON)cos(MON)
Substituting OM = OA/2 and ON = OB/2, we get:
MN^2 = OA^2/4 + OB^2/4 - (OA)(OB)/2 cos(BOA)
But MN = OD, so we can also express this as:
OD^2 = (3/7x + 4/7y)^2 = OA^2/4 + OB^2/4 - (OA)(OB)/2 cos(BOA)
Substituting OD^2 = (3/7x + 4/7y)^2 and simplifying, we get:
9x^2 + 16y^2 = 49(OA^2 + OB^2) - 42(OA)(OB) cos(BOA)
Substituting AB^2 = OA^2 + OB^2 - 2(OA)(OB) cos(BOA) and simplifying, we get:
9x^2 + 16y^2 = 49AB^2
Substituting AD = AB/2, we get:
9x^2 + 16y^2 = 49(2AD)^2
Simplifying, we get:
x^2 + 4y^2 = 28AD^2
We want to find the ratio AD:DB, which is the same as the ratio AD:(AB - AD). Substituting AB = 2AD, we get:
AD:(AB - AD) = AD:AD = 1:1
Therefore, the ratio AD:DB is 1:1.
Learn more about triangle at:
https://brainly.com/question/2773823
#SPJ1
2/3=x/6 find the value of x
Answers
Answer: x=4
Step-by-step explanation:

Answer=X=9
3 cm
3 cm
Surface Area
3 cm
=
[?] cm²
Entor
Answers
By multiplying the surface area of one face by six, 54 cm2 is obtained as the area of six faces.
What is a 3 cm by 3 cm cube's surface area?The length of a side squared determines the area of one face. By multiplying the area of one face by six, 54 cm2 is obtained as the area of six faces.Six times the square of the cube's side length is the formula for surface area. It is represented by the number 6a2, where a represents the cube's side length. Basically, it is the whole amount of surface.Height + Breadth + Length equals a. As a result, an is the length of each cube edge. The volume of cube formula is thus a a a = a3.By multiplying the surface area of one face by six, 54 cm2 is obtained as the area of six faces.
To learn more about Surface Area refer to:
https://brainly.com/question/410493
#SPJ1
How many significant figures are in the number
43.6? 43.6 has [?] significant figures.
Answers
Answer:
43.6 has 3 significant figures.
every us state has 2 senators (there are 50 states). if there are 500 members in congress, what percent of the congress is made up of senators?
Answers
Answer:
20% of the Congress is made of Senators.
Step-by-step explanation:
Our whole here is 500, since the House of Representatives and Senate combined would have 500 members in this case. So, we now need to find out how many senators there are.
\(2\) x \(50\) = \(100\)
Now, since we know the fact that there are 100 senators in Congress, we will find out what percent of 500 is 100.
100 = 20% of 500. To check, we will multiply 5 by 100. We get 500.
Therefore, the answer is 20%.
what is the answer for 5 - ( -7) = 5 + _____
write as addition
please give explanation for this
Answers
The complete statement is 5 + 7
What is the commutative property of addition?The commutative property of addition is a mathematical rule stating that a change in the order or arrangement of the numbers being added does not affect the sum.
It is also important to note the following sign changes;
(-) (-) = +
(+) (+) = +
(-)(+) = -
(+)(-) = -
Given the expression;
5 - ( -7)
We know that the signs (-)(-) is equivalent to (+) sign
Substitute into the expression;
5 + 7
Thus, the complete statement is 5 + 7
Learn more about addition here:
https://brainly.com/question/4721701
#SPJ1
For her phone service, Melissa pays a monthly fee of $16, and she pays an additional $0.06 per minute of use. The least she has been charged in a month is $93.22. What are the possible numbers of minutes she has used her phone in a month? Use m for the number of minutes, and solve your inequality for m.
Answers
Answer:
1287
Step-by-step explanation:
93.22-16=77.22
77.22 devided by 0.06=1287
Which value below is included in the solution set for the inequality statement? -3(x-4) > 6(x-1) 0-1 02 07 0 3 NEXT QUESTION ASK FOR HELP
Answers
The solution set for the inequality is x < 2. Among the given options, the value that is included in the solution set is 0.
To determine which value is included in the solution set for the inequality statement -3(x-4) > 6(x-1), we need to solve the inequality for x.
Starting with the given inequality:
-3(x - 4) > 6(x - 1)
First, distribute -3 and 6 to the terms inside the parentheses:
-3x + 12 > 6x - 6
Next, combine like terms by subtracting 6x from both sides and adding 6 to both sides:
-3x - 6x > -6 - 12
-9x > -18
To isolate x, divide both sides of the inequality by -9. Remember that when dividing by a negative number, we need to reverse the inequality sign:
x < (-18) / (-9)
x < 2
Therefore, the solution set for the inequality is x < 2. Among the given options, the value that is included in the solution set is 0.
for such more question on inequality
https://brainly.com/question/17448505
#SPJ8
What is the quotient of 5/7 divided 3 1/3
Answers
Answer:
4 1/21 is the answer
What is the solution of the equation
5 = 22?
Answers
Answer:X=17
Step-by-step explanation:
Im not 100% sure
In art class students are mixing blue and red paint to make purple paint. Isaiah mixes 3 cups of blue paint and 7 cups of red paint. Casho mixes 4 cups of blue paint and 13 cups of red paint. Use Isaiah and Casho's percent of red paint to determine whose purple paint will be redder.
Answers
Based on the percent of red paint, Casho's purple paint will be redder than Isaiah's.
To determine whose purple paint will be redder based on the percent of red paint, we need to compare the ratios of red paint to the total paint used by Isaiah and Casho.
Isaiah's Ratio:
Isaiah mixes 3 cups of blue paint and 7 cups of red paint, making a total of 3 + 7 = 10 cups of paint.
To calculate the percent of red paint, we divide the amount of red paint (7 cups) by the total amount of paint (10 cups) and multiply by 100 to get the percentage:
Red paint percentage for Isaiah = (7 cups / 10 cups) * 100 = 70%
Casho's Ratio:
Casho mixes 4 cups of blue paint and 13 cups of red paint, making a total of 4 + 13 = 17 cups of paint.
To calculate the percent of red paint, we divide the amount of red paint (13 cups) by the total amount of paint (17 cups) and multiply by 100 to get the percentage:
Red paint percentage for Casho = (13 cups / 17 cups) * 100 = 76.47% (rounded to two decimal places)
Comparing the percentages, we can see that Casho's purple paint will be redder because Casho's paint has a higher percentage of red paint (76.47%) compared to Isaiah's paint (70%).
Therefore, based on the percent of red paint, Casho's purple paint will be redder than Isaiah's.
for such more question on percent
https://brainly.com/question/24877689
#SPJ8
Which graph represents the function g(z)=√2-1+1?
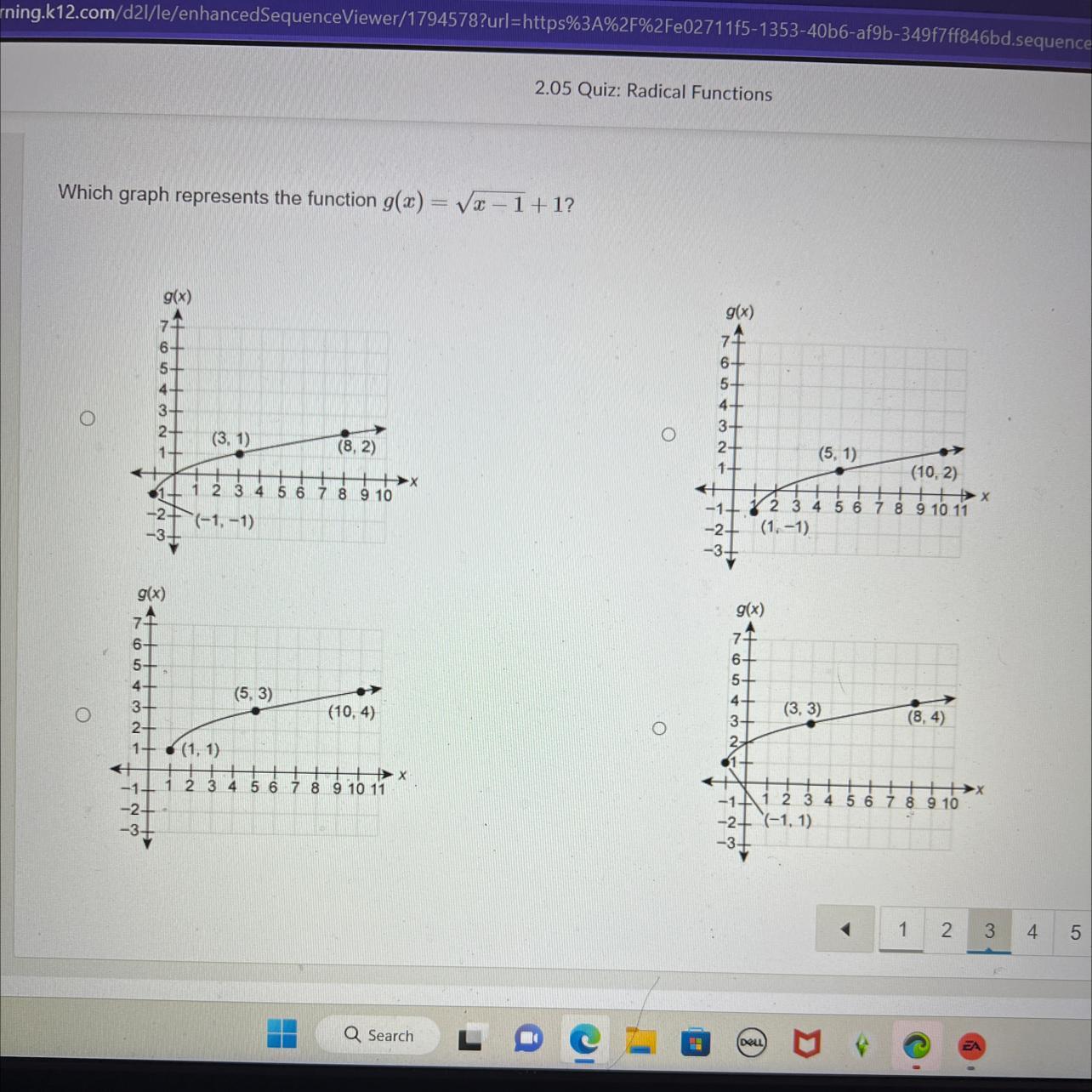
Answers
In response to the given question, we can state that Because it is independent of z, the function g(z) is a constant function. In particular, g(z) equals 2 - 1 + 1 = 2.
what is function?Mathematicians examine numbers and complex variations, equations and associated structures, forms and their locations, and prospective positions for these things. The term "functioning" signifies the connection between a collection of inputs, each of which has a corresponding output. A function is a connection of inputs and results in which each input leads to a single, identifiable outcome. Each function is assigned a domain, a codomain, or a scope. The letter f is widely used this to denote functions (x). The symbol for admission is an x. The four primary types of usable functions are on operations, one-to-one capabilities, so multiple functionality, in capabilities, and then on functions.
Because it is independent of z, the function g(z) is a constant function. In particular, g(z) equals 2 - 1 + 1 = 2.
To know more about function visit:
https://brainly.com/question/28193995
#SPJ1
a small library has 4 times as many story books as puzzle books. if it has 32 puzzle books, how many story books does it have?
Answers
I need Help please!!!

Answers
Step-by-step explanation:
it seems you solved the tricky part yourself already.
just to be sure, let's do the first derivative here again.
the easiest way would be for me to simply multiply the functional expression out and then do a simple derivative action ...
f(t) = (t² + 6t + 7)(3t² + 3) = 3t⁴ + 3t² + 18t³ + 18t + 21t² + 21 =
= 3t⁴ + 18t³ + 24t² + 18t + 21
f'(t) = 12t³ + 54t² + 48t + 18
and now comes the simple part (what was your problem here, don't you know how functions work ? then you are in a completely wrong class doing derivatives; for that you need to understand what functions are, and how they work). we calculate the function result of f'(2).
we simply put the input number (2) at every place of the input variable (t).
so,
f'(2) = 12×2³ + 54×2² + 48×2 + 18 = 96 + 216 + 96 + 18 =
= 426
can you please help me with this

Answers
Sathish will be going to pay a total of $64.8 for the gas.
What is the arithmetic operator?Arithmetic operators are four basic mathematical operations in which summation, subtraction, division, and multiplication involve.,
Summation = addition of two or more numbers or variable
For example = 2 + 8 + 9
Subtraction = Minus of any two or more numbers with each other called subtraction.
For example = 4 - 8
Division = divide any two numbers or variable called division.
For example 4/8
Multiplication = to multiply any two or more numbers or variables called multiplication.
For example 5 × 7.
The First 150 and last 150 km will cover by Satish only
Since 6 liters covers 100 km
So,
Cost of 300 km (18 liters) ⇒ 18×1.2 = 21.6
Now,
The journey 2100 - 300 = 1800 km has been covered by all three
Split 1800/3 = 600 km of money Satish will pay
So,
Cost of 600km(36 liters) ⇒ 36 × 1.2 = 43.2
Total paid = 21.6 + 43.2 = 64.8.
Hence "Satis will be going to pay a total of $64.8 for the gas".
To learn more about the arithmetic operators,
brainly.com/question/25834626
#SPJ1
I need expert answers for this

Answers
The last expression finally simplifies to cot β + tan α using quotient identity in trigonometric identities.
How to prove Trigonometric Identities?We want to verify the trigonometric identity;
cos (α - β)/(cos α sin β) = cot β + tan α
Now, according to trigonometric identities in mathematics, we know that;
cos (α - β) = (cos α cos β) + (sin α sin β)
Thus, plugging that back into our left hand side of the main question gives;
[(cos α cos β) + (sin α sin β)]/(cos α sin β)
Rewriting this expression by separating the denominator gives;
[(cos α cos β)/(cos α sin β)] + [(sin α sin β)]/(cos α sin β)
Using quotient identities, this can be simplified to;
cot β + tan α
Read more about Trigonometric Identities at; https://brainly.com/question/7331447
#SPJ1
Select the correct answer.
Function bis nonlinear, and b(9) = 4. Which equation could represent function b?
Answers
The nonlinear- function which represents b(9)=4 is given by b(x)=72/x - 4 .
In mathematics and physics, a nonlinear system is one in which the change in the output is not proportional to the change in the input. Engineers, biologists, physicists, mathematicians, and many other scientists are interested in nonlinear problems since the majority of systems are inherently nonlinear.
Nonlinear function graphs don't resemble lines at all. It contains the formula f(x) = ax + b. Its equation can take any form, with the exception of f(x) = ax + b. The slope of the curve is the same between any two points. The point pairs on the graph do not all have equal slopes.
Of all the given options: the only equations which imply that b(9)=4 are :
i) b(x)=72/x - 4 and (iv) b(x)=4
Of this two options only the first option is non-linear.
Hence the required option is b(x)=72/x - 4 .
To learn more about nonlinear function visit:
https://brainly.com/question/5758609
Disclaimer:
The missing options are:
i) b(x) = 72/x - 4
ii) b(x) = √x + 7
iii)b(x) = 2x+1
iv) b(x) = 4
#SPJ1
Which of the expression represents the Commutative Property of Addition?

Answers
Which ones right ????
