Twice the quotient of a number and -24 is -8 Find the number.
The number is ________.
Answers
The number for the given quotient is obtained as 6.
What are arithmetic operations?The arithmetic operations are the fundamentals of all mathematical operations. The example of these operators are addition, subtraction, multiplication and division. These operations follow the rule of PEDMAS which states that the priority should be given to the operators that comes first in the word PEDMAS.
Suppose the number be x.
Then, as per the question the following equation can be written as,
2(-24 ÷ x) = -8
⇒ -24 ÷ x = -4
⇒ x = -24 ÷ -4
⇒ x = 6
Hence, the required number is 6.
To know more about arithmetic operation click on,
https://brainly.com/question/25834626
#SPJ5
Related Questions
What are the variables in this expression?
f + 2g + h/4 - 7
A) f and g only
B) g and h only
C) f, g, and -7 only
D) f, g, and h only
Answers
hope this helps :)
Please help and hurry 15 points
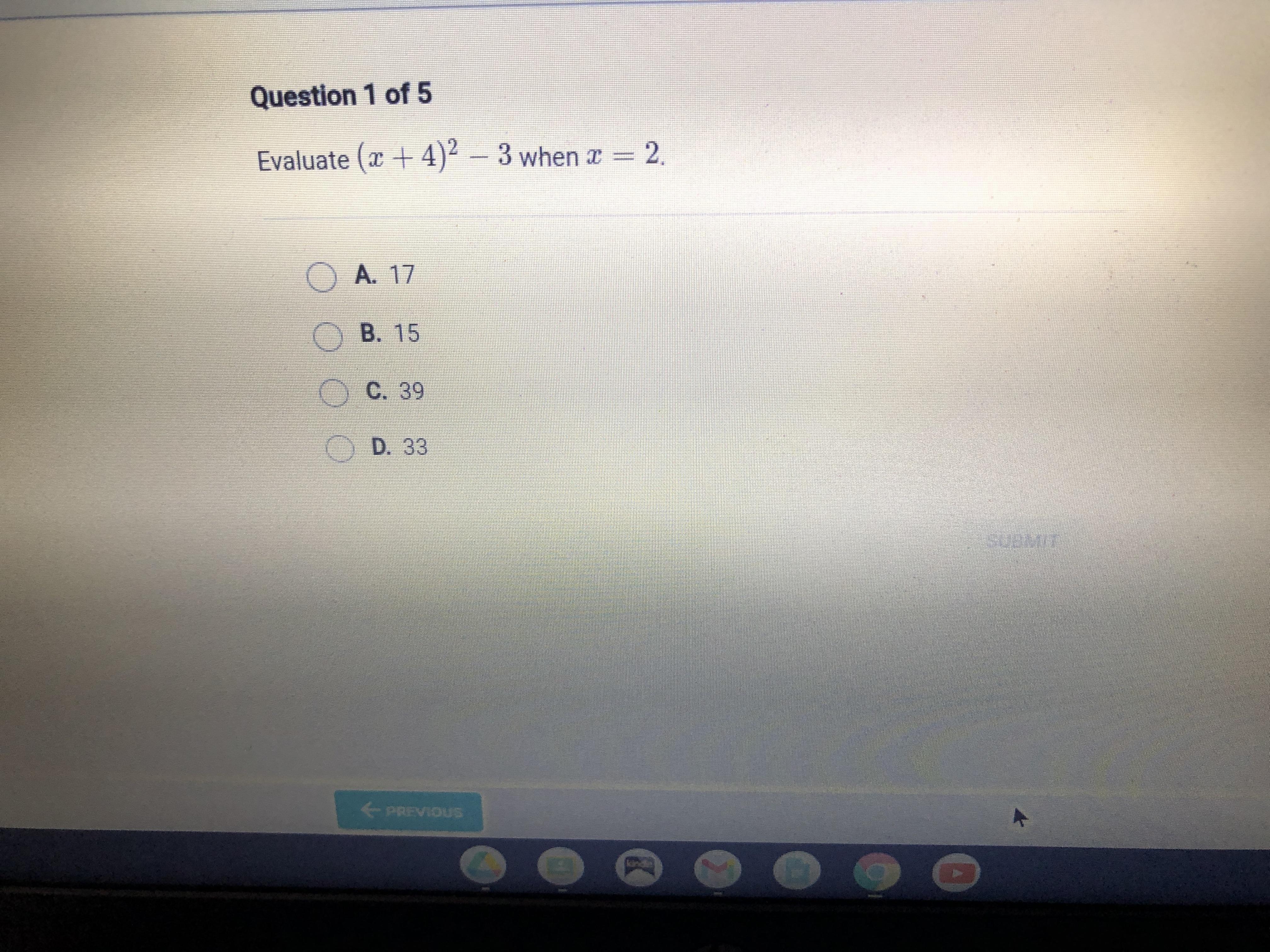
Answers
So substitute the x for 2
(2+4)^2-3
Pemdas
6^2
36-3
33
Answer:
23
Step-by-step explanation:
(x+4) ²-3 (Question)
x²+4x+16-3
x²+4x+13
(2)²+4(2)+13 (since x=2)
4+6+13
23
Find an equation for the line, in the indicated form, with the
given properties.4)Containing the points (-2,2) and (7,-4);
slope-intercept form
Answers
To find the equation of a line in slope-intercept form (y = mx + b) that passes through the points (-2, 2) and (7, -4), we first need to determine the slope (m) of the line.
The slope (m) can be calculated using the formula:
m = (y2 - y1) / (x2 - x1)
Substituting the coordinates (-2, 2) and (7, -4) into the formula, we get:
m = (-4 - 2) / (7 - (-2)) = -6 / 9 = -2/3
Now that we have the slope (m), we can use it along with one of the given points to find the y-intercept (b).
Let's use the point (-2, 2) and substitute the values into the slope-intercept form:
2 = (-2/3)(-2) + b
2 = 4/3 + b
b = 2 - 4/3
b = 2/3
Therefore, the equation of the line in slope-intercept form is:
y = (-2/3)x + 2/3
By using the formula for slope, we calculate the slope of the line passing through the given points. Substituting one of the points into the slope-intercept form equation, we solve for the y-intercept. Finally, we combine the slope and y-intercept to obtain the equation of the line in slope-intercept form, which is y = (-2/3)x + 2/3.
Learn more about equation here : brainly.com/question/22277991
#SPJ11
what’s the answer did anyone figure it out ?
Answers
Answer:
NAswer to what
Step-by-step explanation:
two diagonals of a regular heptagon (a $7$-sided polygon) are chosen. what is the probability that they intersect inside the heptagon?
Answers
14 diagonals is the probability that they intersect inside the heptagon.
What are examples and probability?
It is based on the probabilities that something could happen. The logic underpinning probability serves as the foundation for theoretical probability.A coin is tossed, for instance, and the theoretical likelihood of receiving a head is 1 in 2.A probability is a number that expresses the possibility or likelihood that a specific event will take place.Both proportions between 0 and 1 and percentages between 0% and 100% can be used to describe probabilities.there are 14 diagonals, not 30 diagonals.
This can be found by
\(\frac{n(n - 3)}{2} = \frac{7 * 4}{2}\) = 14 diagonals.
= 28+42/182(5/13),
because we can choose the first diagonal is 14 ways, the second is 13.
Learn more about probability
brainly.com/question/11234923
#SPJ4
to make 6 servings of soup, you need 5 cups of chicken broth. you want to know how many servings you can make with 2 quarts of chicken broth. which proportion should you use?
Answers
since we cannot have a fraction of a serving, we can only make 9 servings of soup with 2 quarts (or 8 cups) of chicken broth. Therefore, the proportion we should use is 5 cups of chicken broth to 6 servings of soup.
To answer this question, we need to convert 2 quarts to cups. Since there are 4 cups in a quart, 2 quarts would be 8 cups.
Now that we know we have 8 cups of chicken broth, we can set up a proportion to determine how many servings of soup we can make.
5 cups of chicken broth = 6 servings of soup
x cups of chicken broth = y servings of soup
To solve for x and y, we can cross-multiply:
5y = 6x
x = 8 cups of chicken broth
y = (6/5) * 8 = 9.6 servings of soup
However, since we cannot have a fraction of a serving, we can only make 9 servings of soup with 2 quarts (or 8 cups) of chicken broth.
Therefore, the proportion we should use is 5 cups of chicken broth to 6 servings of soup.
To determine how many servings you can make with 2 quarts of chicken broth, you should set up a proportion using the given information: 6 servings require 5 cups of broth. First, convert 2 quarts to cups (1 quart = 4 cups, so 2 quarts = 8 cups). Now, set up the proportion:
6 servings / 5 cups = x servings / 8 cups
Here, x represents the number of servings you can make with 8 cups (2 quarts) of chicken broth. By cross-multiplying and solving for x, you will find the number of servings possible with the available broth.
Visit here to learn more about cross-multiply : https://brainly.com/question/30764437
#SPJ11
What are the four things
that make up
galaxy ? I need a answer quickly and I need it to be correct! I need a answer ASAP! Thanks
Answers
Find the percent of the total area under the standard normal curve between the following z-scores. z=−1.5 and z=−0.7 The percent of the total area between z=−1.5 and z=−0.7 is %. (Round to the nearest integer.)
Answers
The percent of the total area under the standard normal curve between z = -1.5 and z = -0.7 is 18%.
To find the percent of the total area between two z-scores, we need to calculate the area under the standard normal curve between those two z-scores.
Using a standard normal distribution table or a statistical software, we can find the area to the left of each z-score and subtract the smaller area from the larger area to find the area between the z-scores.
For z = -1.5, the area to the left of z = -1.5 is approximately 0.0668.
For z = -0.7, the area to the left of z = -0.7 is approximately 0.2420.
The area between z = -1.5 and z = -0.7 is:
Area between z = -1.5 and z = -0.7 = Area to the left of z = -0.7 - Area to the left of z = -1.5
= 0.2420 - 0.0668
= 0.1752
To convert this area to a percentage, we multiply by 100:
Percentage of the total area between z = -1.5 and z = -0.7 = 0.1752 * 100 ≈ 17.52%
Rounding to the nearest integer, the percent of the total area between z = -1.5 and z = -0.7 is 18%.
The percent of the total area under the standard normal curve between z = -1.5 and z = -0.7 is approximately 18%.
To know more about percent , visit;
https://brainly.com/question/31323953
#SPJ11
Help me I will give brainliest to you, help me



Answers
Answer:
1) 46 cases to 1 min
2) 50 cans to 1 min
3) Cans are made faster
Step-by-step explanation:
1) 2 min per 92 cases so that's 2/2 and 92/2 which is 1 to 46
2) Now canned juice is as it shows in the graph as 50 cans per min.
3) 50 cans can be made in a min while only 46 cases can be made in a min.
if all your ancestors were extinct, what would be the total number of your ancestors for the past 42 generations (counting your parents' generation as number one)? (hint: use the formula for the sum of a geometric sequence.)
Answers
Answer:
The total number of your ancestors for the past 42 generations would be 8,796,093,022,206.
Step-by-step explanation:
To calculate the total number of your ancestors for the past 42 generations, we can use the formula for the sum of a geometric sequence:
Sum = a * (1 - r^n) / (1 - r)
where: - a is the first term in the sequence - r is the common ratio between terms - n is the number of terms in the sequence
For this problem: - a = 2 (since you have 2 parents) - r = 2 (each generation doubles the number of ancestors) - n = 42 (the number of generations)
Now, plug these values into the formula:
Sum = 2 * (1 - 2^42) / (1 - 2) Sum = 2 * (1 - 4398046511104) / (-1) Sum = 2 * (4398046511103) / 1 Sum = 8796093022206
So, the total number of your ancestors for the past 42 generations would be 8,796,093,022,206.
Know more about geometric sequence,
https://brainly.com/question/30376337
#SPJ11
Give cb/ba = de/ef find BA

Answers
The value of BA = 11.2
Determining the length of BA:Here we use the condition CB/BA = DE/EF to determine the Length of BA
Substitute the lengthS of each side as per the given figure and solve the condition for the Length of the side BA.
Given that CB/BA = DE/EF
From the given figure,
CB = 7, DE = 5, and EF = 8
Substitute the above values in the given condition
=> 7 /BA = 5 /8
Do cross multiplication
=> BA(5) = 7(8)
=> 5BA = 56
=> BA = 11.2
Therefore,
The value of BA = 11.2
Learn more about Length of the side at
https://brainly.com/question/12386987
#SPJ1
$600 at 4% for 9 months.
Answers
The simple interest for the principal amount of $600 at the rate of 4% for 9 months will be equal to $216.
What is Simple interest?A quick and simple way to figure out interest on that money is to use the simple interest approach, which adds interest at the same rate for each daily cycle, and it is to the initial principal amount. A way to figure out how much interest will be charged on an amount of money at a specific rate and for a specific duration of time is by using simple interest.
As per the given information in the question,
Principle amount, P = $600
Time, T = 9 months
Rate, R = 4%
SI = (600 × 9 × 4)/100
SI = $216.
The SI will be $216.
To know more about Simple interest:
https://brainly.com/question/25845758
#SPJ2
What is an equation of the line that passes through the point (4,2)(4,2) and is perpendicular to the line 4x+3y=214x+3y=21?
Answers
keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above
\(4x+3y=21\implies 3y=-4x+21\implies y=\cfrac{-4x+21}{3} \\\\\\ y=\stackrel{\stackrel{m}{\downarrow }}{-\cfrac{4}{3}}x+7\qquad \impliedby \qquad \begin{array}{|c|ll} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{\cfrac{-4}{3}} ~\hfill \stackrel{reciprocal}{\cfrac{3}{-4}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{3}{-4}\implies \cfrac{3}{4}}}\)
so we're really looking for the equation of a line whose slope is 3/4 and it passes through (4 , 2)
\((\stackrel{x_1}{4}~,~\stackrel{y_1}{2})\hspace{10em} \stackrel{slope}{m} ~=~ \cfrac{3}{4} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{2}=\stackrel{m}{ \cfrac{3}{4}}(x-\stackrel{x_1}{4}) \\\\\\ y-2=\cfrac{3}{4}x-3\implies {\Large \begin{array}{llll} y=\cfrac{3}{4}x-1 \end{array}}\)
Separate the number 27 into two
parts so that the first number is twice
the second number. What are the
numbers?
Answers
Answer:
18 and 9 are the numbers
Find the area 3/4 circle with the radius of 4.
THXXXXX
Answers
Step-by-step explanation:
If you were asking what is the 3/4 the area of circle with radius 4 I can answer this.
The area of a circle with radius 4 is π4 ^2=16π
3/4*16π= 12π, thus your answer.
Consider a circle with center C(5,8) that contains the point P(1,2) What is the radius? What is the circle equation?
Answers
Answer:
see explanation
Step-by-step explanation:
the radius r is the distance from the centre to a point on the circle.
calculate the radius using the distance formula
d = \(\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2 }\)
with (x₁, y₁ ) = P (1, 2 ) and (x₂, y₂ ) = C (5, 8 )
r = \(\sqrt{(5-1)^2+(8-2)^2}\)
= \(\sqrt{4^2+6^2}\)
= \(\sqrt{16+36}\)
= \(\sqrt{52}\)
the equation of a circle in standard form is
(x - h )² + (y - k )² = r²
where (h, k ) are the coordinates of the centre and r is the radius
here (h, k ) = C (5, 8 ) and r = \(\sqrt{52}\) , then
(x - 5 )² + (y - 8 )² = ( \(\sqrt{52}\) )² , that is
(x - 5)² + (y - 8)² = 52
GEOMETRY A diagonal is a line segment
that connects two non adjacent vertices.
Find the number of diagonals in an
octagon.
Answers
9600 is invested at 8% per annum simple interest for 5 years
Answers
Answer:
$3,840
Step-by-step explanation:
9600 x 0.08 = 768 per years (assuming flat rate)
768x5= 3,840
Answer:
3840
Step-by-step explanation:
9600 * 8% * 5 = 3840
Hope this helps!
Thenks and mark me brainliest :))
An acute angle, θ, is in a right triangle such that sin of theta is equal to 3 over 8 period What is the value of cot θ?
square root of 55 over 3
the quantity 3 times the square root of 55 end quantity over 55
square root of 55 over 8
the quantity 8 times the square root of 55 end quantity over 5
Answers
We want to find the value of cot(θ) given that sin(θ) = 3/8 and θ is an angle in a right triangle, we will get:
cot(θ) = (√55)/3
So we know that θ is an acute angle in a right triangle, and we get:
sin(θ) = 3/8
Remember that:
sin(θ) = (opposite cathetus)/(hypotenuse)hypotenuse = √( (opposite cathetus)^2 + (adjacent cathetus)^2)Then we have:
opposite cathetus = 3
hypotenuse = 8 = √(3^2 + (adjacent cathetus)^2)
Now we can solve this for the adjacent cathetus, so we get:
adjacent cathetus = √(8^2 - 3^2) = √55
And we know that:
cot(θ) = (adjacent cathetus)/(opposite cathetus)
Then we get:
cot(θ) = (√55)/3
If you want to learn more, you can read:
https://brainly.com/question/15345177
Question below plz answer it fast!

Answers
Answer:
The answer is 49 .
Step-by-step explanation:
Do i need to explain ?
Mortgage companies usually charge interest semi-annually. What would be the effective rate of interest on a mortgage at 8.15 percent compounded semi-annually? O a. 8.23 percent O b. 8.32 percent O c. 8.46 percent O d. 8.40 percent If you want to save $1,000,000 for retirement with $200 monthly deposits (end-of-month) at 6 percent interest compounded monthly, how long will it take? O a. 54.4 years O b. 55.9 years O c. 52.8 years O d. 57.2 years
Answers
a) The effective rate of interest on a mortgage at 8.15 percent compounded semi-annually is 8.23 percent.
b) It will take approximately 54.4 years to save $1,000,000 for retirement with $200 monthly deposits at 6 percent interest compounded monthly.
a) To find the effective rate of interest, we use the formula: Effective Rate = (1 + (Nominal Rate / Number of Compounding Periods))^Number of Compounding Periods - 1.
For a mortgage at 8.15 percent compounded semi-annually, the nominal rate is 8.15 percent and the number of compounding periods is 2 per year.
Plugging these values into the formula, we get Effective Rate = (1 + (0.0815 / 2))^2 - 1 ≈ 0.0823, or 8.23 percent. Therefore, the effective rate of interest on the mortgage is 8.23 percent.
b) To determine how long it will take to save $1,000,000 for retirement with $200 monthly deposits at 6 percent interest compounded monthly, we can use the formula for the future value of an ordinary annuity: FV = P * ((1 + r)^n - 1) / r, where FV is the future value, P is the monthly deposit, r is the monthly interest rate, and n is the number of periods.
Rearranging the formula to solve for n, we have n = log(FV * r / P + 1) / log(1 + r). Plugging in the values $1,000,000 for FV, $200 for P, and 6 percent divided by 12 for r, we get n = log(1,000,000 * (0.06/12) / 200 + 1) / log(1 + (0.06/12)) ≈ 54.4 years.
Therefore, it will take approximately 54.4 years to save $1,000,000 for retirement under these conditions.
Learn more about interest rate here:
https://brainly.com/question/32020793
#SPJ11
an extraneous solution is a value that appears to be part of the solution set. but when tested it does not create a true statement x-1=√x+1
Answers
The extraneous solution of the equation x - 1 = √x + 1 is x = 0
How to determine the extraneous solutionFrom the question, we have the following parameters that can be used in our computation:
x - 1 = √x + 1
Take the square of both sides
So, we have
x² - 2x + 1 = x + 1
Evaluate the like terms
x² - 3x = 0
So, we have
x(x - 3) = 0
Solving for x, we have
x = 3 and x = 0
Substitute x = 3 and x = 0 in x - 1 = √x + 1
3 - 1 = √3 + 1
2 = 2 ---- true
0 - 1 = √0 + 1
-1 = 1 ---- false
Hence, the extraneous solution is x = 0
Read more about extraneous solution at
https://brainly.com/question/16234285
#SPJ1
a rectangular storage container without a lid is to have a volume of 10m3. the length of its base is twice the width. material for the base costs 10$ per square meter. material for the sides costs 6$ per square meter. find the cost of materials for the least expensive such container.
Answers
The cost of materials for the least expensive such container is 245.31 dollars .
Suppose the width of container is x (m),
length of the base of container is 2x (m)
the base area of container is (length × width)sq. m i.e 2x² meter².
Since the volume of container is 10 m³.
the height of container = area of container/ volume of container
height of container= 10/2x² m = 5/x² m
The cost of making such container is cost of base = 2x²*10 = 20x².
cost of sides of container = (2×2x × 5/x² + 2× x × 5/x²)×6 = 180/x
The overall cost is hence the sum of the base and the sides: f(x) = 20x² + 180/x
The get the minimum,
df(x)/dx = 20×(2x - 9/x²) = 0
so 2x = 9/x^2 => 2x = 2.0800 ==> x = 1.651 m
f(x) = 245.31 dollars
To learn more about Maxima or minima, refer:
https://brainly.com/question/14378712
#SPJ4
\( \sqrt{147} - \sqrt{75} + \sqrt{27} \)
Answers
PLEASE HELP ITS DUE IS ONE HOUR !!!

Answers
The correct responses for the points, segments, lines, planes, are as follows;
1. M, S, X, and Y
2. Two lines are; \( \overleftrightarrow{SX}\), \( \overleftrightarrow{YR}\)
3. \( \overline {MX}, \overline{MY}, \overline {MS}, \overline{MR}\)
4. \(\overrightarrow{MT}\)
5. S, M, T
6. T
7. \( \overline{MT}\)
8. \( \overleftrightarrow{SX}\)
9. \( \overleftrightarrow{SX}\)
10. \( \overline{MR}\)
11. A line
12. A plane
13. A point
14. A plane
15. A ray
16. A segment
Please find attached the drawing for the figures in questions 17, 18, 19,and 20
What are the required points, segments, lines, planes and rays?1. A point in Euclidean geometry is a location in space.
Four points are; M, S, X, and Y
2. A line has no thickness and extends indefinitely in both directions.
Two lines are;
\( \overleftrightarrow{SX}\)
\( \overleftrightarrow{YR}\)
3. Four segments are;
\( \overline {MX}, \overline{MY}, \overline {MS}, \overline{MR}\)
4. A ray that has M as an endpoint is \overrightarrow{MT}
5. Three collinear points are; S, M, T
6. A point not on \( \overline{YR}\) is T
7. A segment with points T and M as its endpoints is \( \overline{MT}\)
8. A line that does not contain R is \( \overleftrightarrow{SX}\)
9. A line containing M is; \( \overleftrightarrow{SX}\)
10. A segment of lies on \( \overleftrightarrow{YR}\) is MR
11. A toothpick suggests a line
12. A floor suggests a plane
13. The tip of a pin suggests a point
14. The water surface of a swimming pool suggest a plane
15. A beam of light from a laser suggests a ray
16. A fence pole suggests a segment
Please find attached the drawing for the figures in questions 17, 18, 19, and 20
Learn more about points, segments, rays, lines, and planes here:
https://brainly.com/question/13241707
#SPJ1

Solve for measure of angle A.

Answers
1/2(44)
22
The measure of angle a is:
a = (140° - 96°) / 2 = 44° / 2 = 22°
Therefore, the answer is 22.
1
If two secant lines intersect outside a circle, the measure of the angle formed by the two lines is one half the positive difference of the measures of the intercepted arcs.
In the given diagram, we can see that the intercepted arcs are 96° and 140°. Therefore, the measure of angle a is:
a = (140° - 96°) / 2 = 44° / 2 = 22°
Therefore, the answer is 22.
Answer: 22
To know more about vectors
https://brainly.com/question/28028700
#SPJ3
Juanita studied 3/2 hours on Saturday and 5/4 hours on Sunday. How many total hours did she study those two days?
Answers
Answer:
11/4
Step-by-step explanation:
3/2 can be re-written as 6/4. they now have the same denominator. 6/4 + 5/4 = 11/4
Let theta be an acute angle of a right triangle. Find the values of the other five trigonometric functions of theta.

Answers
The exact values of the remaining trigonometric functions are listed below:
Case 3: cos θ = 3 / 5, tan θ = 4 / 3, cot θ = 3 / 4, sec θ = 5 / 3, csc θ = 5 / 4
Case 4: sin θ = √11 / 6, tan θ = √11 / 5, cot θ = 5√11 / 5, sec θ = 6 / 5, csc θ = 6√11 / 11
Case 5: cos θ = 8√73 / 73, sin θ = 3√73 / 73, tan θ = 3 / 8, cot θ = 8 / 3, csc θ = √73 / 3
Case 6: sin θ = 1 / 2, cos θ = √3 / 2, tan θ = √3 / 3, sec θ = 2√3 / 3, csc θ = 2
How to find the exact values of trigonometric functions
In this problem we find four cases of trigonometric functions, whose exact values of remaining trigonometric functions must be found. The trigonometric functions are defined below:
sin θ = y / √(x² + y²)
cos θ = x / √(x² + y²)
tan θ = y / x
cot θ = x / y
sec θ = √(x² + y²) / x
csc θ = √(x² + y²) / y
Now we proceed to determine the exact values of the trigonometric functions:
Case 3: y = 4, √(x² + y²) = 5
x = √(5² - 4²)
x = 3
cos θ = 3 / 5
tan θ = 4 / 3
cot θ = 3 / 4
sec θ = 5 / 3
csc θ = 5 / 4
Case 4: x = 5, √(x² + y²) = 6
y = √(6² - 5²)
y = √11
sin θ = √11 / 6
tan θ = √11 / 5
cot θ = 5√11 / 5
sec θ = 6 / 5
csc θ = 6√11 / 11
Case 5: x = 8, √(x² + y²) = √73
y = √(73 - 8²)
y = 3
cos θ = 8√73 / 73
sin θ = 3√73 / 73
tan θ = 3 / 8
cot θ = 8 / 3
csc θ = √73 / 3
Case 6: x = √3, y = 1
sin θ = 1 / 2
cos θ = √3 / 2
tan θ = √3 / 3
sec θ = 2√3 / 3
csc θ = 2
To learn more on trigonometric functions: https://brainly.com/question/25618616
#SPJ1
Which of these equations have no solution? Check all that apply.
a.) 2(x + 2) + 2 = 2(x + 3) + 1
b.) 2x + 3(x + 5) = 5(x – 3)
c.) 4(x + 3) = x + 12
d.) 4 – (2x + 5) = (–4x – 2)
e.) 5(x + 4) – x = 4(x + 5) – 1
Answers
Answer:
A, B, and C
Step-by-step explanation:
Answer:
a.) 2(x + 2) + 2 = 2(x + 3) + 1
b.) 2x + 3(x + 5) = 5(x – 3)
e.) 5(x + 4) – x = 4(x + 5) – 1
Step-by-step explanation:
a.) 2(x + 2) + 2 = 2(x + 3) + 1
0 ≠ 1
b.) 2x + 3(x + 5) = 5(x – 3)
0 ≠ -30
c.) 4(x + 3) = x + 12
x = 3
d.) 4 – (2x + 5) = (–4x – 2)
x = -½
e.) 5(x + 4) – x = 4(x + 5) – 1
0 ≠ -1
I hope this helps
Mk, someone knows this answer. I know it! Pwease help!

Answers
Answer:
16(base) x 15(height) x 1/2(basically just dividing by 2) = 120
120 x 2 = 240
17 x 17 = 289, 289 x 2 = 578
17 x 16 = 272
Add all given areas:
240 + 272 + 578 = 1,090 in2 is your answer