Answers
Answer:
B
Step-by-step explanation:
Using Pythagoras' identity in right triangle ABC
The square on the hypotenuse is equal to the sum of the squares on the other 2 sides, that is
AB² + AC² = BC² , substitute values
5² + AC² = 13²
25 + AC² = 169 ( subtract 25 from both sides )
AC² = 144 ( take the square root of both sides )
AC = \(\sqrt{144}\) = 12
Since the triangles are congruent then corresponding sides are congruent, then
DE = AC = 12 inches → B
Related Questions
Use a triple integral to find the volume of the solid enclosed by the paraboloids y = x^2 + z^2 and y = 32 - x^2 - z^2
Answers
The volume of the solid enclosed by the two paraboloids is approximately 1365.34π cubic units.
Here, we have to find the volume of the solid enclosed by the two paraboloids \(y = x^2 + z^2\) and \(y = 32 - x^2 - z^2\),
we need to set up a triple integral in cylindrical coordinates.
In cylindrical coordinates, we have:
x = r cos(θ)
z = r sin(θ)
y = y
The limits of integration for r, θ, and y will depend on the region of integration.
First, let's find the intersection points of the two paraboloids:
\(x^2 + z^2 = 32 - x^2 - z^2\\2x^2 + 2z^2 = 32\\x^2 + z^2 = 16\)
This represents a circular region with radius r = 4 in the x-z plane.
Now, let's find the limits of integration for r, θ, and y:
For r:
Since the circular region has a radius of 4, the limits of r will be from 0 to 4.
0 ≤ r ≤ 4
For θ:
The intersection points form a complete circle in the x-z plane, so the limits of θ will be from 0 to 2π.
0 ≤ θ ≤ 2π
For y:
The lower paraboloid is given by \(y = x^2 + z^2\), and the upper paraboloid is given by \(y = 32 - x^2 - z^2\).
The limits of y will be from the lower paraboloid to the upper paraboloid.
\(x^2 + z^2 \leq y \leq 32 - x^2 - z^2\)
Now, we can set up the triple integral to find the volume V:
V = ∫∫∫ (y) dy dθ dr
V = ∫∫∫ \((r^2 cos^2(\theta) + r^2 sin^2(\theta)) dy d\theta dr\)
V = ∫∫∫ \((r^2) dy d\theta dr\)
V = ∫∫ \((r^2) y|_{(x^2+z^2)}^{(32-x^2-z^2)} d\theta dr\)
V = ∫∫ \((r^2) (32 - 2x^2 - 2z^2) d\theta dr\)
V = ∫ \((32r^2 - 2r^2(x^2 + z^2)) d\theta dr\)
V = ∫ \((32r^2 - 2r^2r^2) d\theta dr\)
V = ∫ \((32r^2 - 2r^4) d\theta dr\)
Now, integrate with respect to θ from 0 to 2π:
V = ∫(0 to 2π) ∫(0 to 4) \((32r^2 - 2r^4)\) dr dθ
Now, integrate with respect to r from 0 to 4:
V = ∫(0 to 2π) \([(32/3)r^3 - (1/3)r^5] |_0 ^4\) dθ
V = ∫(0 to 2π) \([(32/3)(4^3) - (1/3)(4^5)]\) dθ
V = ∫(0 to 2π) [(32/3)(64) - (1/3)(1024)] dθ
V = ∫(0 to 2π) [682.67] dθ
V = 682.67 * (2π) - 682.67 * (0)
V = 1365.34π cubic units
Therefore, the volume of the solid enclosed by the two paraboloids is approximately 1365.34π cubic units.
To know more about Paraboloids visit:
brainly.com/question/14307074
#SPJ12
I don't get this at all and I need help

Answers
Answer:
Fraction: 63/100, Decimal 0.63
Step-by-step explanation:
Nayeli is a
75
7575 page manuscript. Filémon is a
40
4040 page manuscript.
Since proofreading is faster, Nayeli completes
11
1111 pages an hour, but Filémon only completes
4
44 pages an hour.
When Nayeli and Filémon have the same number of pages left, how many pages will that be
Answers
Answer:
20 pages
Step-by-step explanation:
Which of the rays or segments below IS chord of circle O?
UD
GR
UO
GD
Answers
A chord of a circle is a segment that connects two points on the circle. Therefore, in order to determine which of the rays or segments below is a chord of circle O, we need to identify which of them connects two points on the circle.
- UD: This is a ray that starts at point U and extends indefinitely in the direction of point D. It does not connect two points on the circle, so it is not a chord of circle O.
- GR: This is a segment that connects point G and point R. However, neither of these points is on circle O, so this segment is not a chord of circle O.
- UO: This is a segment that connects point U and point O. Both of these points are on circle O, so this segment is a chord of circle O.
- GD: This is a ray that starts at point G and extends indefinitely in the direction of point D. It does not connect two points on the circle, so it is not a chord of circle O.
To know more about chord visit:-
https://brainly.com/question/21686011
#SPJ11
The coordinate grid shows three points P, Q, and R:
PLEASE HELP!!!!!!!!
A four-quadrant coordinate grid from negative 10 to positive 10 in increments of 2 is drawn. Point P is plotted on the ordered pair negative 6, negative 2. Point Q is plotted on the ordered pair negative 6, negative 6. Point R is plotted on the ordered pair 4, negative 6.
The distance between Q and R is ______ units.
Answers
Answer:
the answer is 10 the other dude is right
Step-by-step explanation:
Answer:
10
Step-by-step explanation:i just took the test and got it right :)
a bicycle is sold at Rs 9040 after allowing 20% discount and imposing 13% vat find the Marked price of the bicycle
Answers
Answer:
sp with vat=9040
d=20%
vat=13%
mp=?
Step-by-step explanation:
sp with vat=9040
sp+vat%of sp=9040
sp(1+13/100)=9040
sp=9040/1.13=8000
mp=sp+d%ofmpmp-d%ofmp=spmp(1-20/100)=8000mp=8000/0.8=10000Write the equation of the line in slope-intercept form that goes through the points (4, -2) and (8, -9)
Answers
Answer:
y = 17/6 x - 40/3
Step-by-step explanation:
Slope-intercept form: y = mx + b
First, let's find the slope:
slope formula: (y2-y1) divded by (x2-x1)
(4, -2) and (8, -9)
(-9 - 8) divded by (-2 - 4) = 17/6
We found m, now we have to find b.
The new equation: y = 17/6 x + b
Insert any of the two points, in this case, I'll insert (4, -2)
-2 = 17/6 (4) + b
-2 = 68/6 + b
b = -2 - 68/6
b = -40/3
Overall equation: y = 17/6 x - 40/3
Steps are on paper.

Suppose $726.56 is deposited at the end of every six months into an account earning 6.45% compounded semi-annually. If the balance in the account four years after the last deposit is to be $31 300.00, how many deposits are needed? (This question asks for 'n')
Answers
We need approximately 10 deposits to reach a balance of $31,300 four years after the last deposit which is compounded semi-annually.
To solve this problem, we can use the formula for the future value of an annuity:
\(FV = P * ((1 + r)^n - 1) / r\)
Where:
FV is the future value of the annuity
P is the periodic payment or deposit amount
r is the interest rate per period
n is the number of periods
In this case, the deposit amount is $726.56, the interest rate is 6.45% compounded semi-annually, and the future value is $31,300. We need to find the number of deposits (n).
We can rearrange the formula and solve for n:
n = log((FV * r) / (P * r + FV)) / log(1 + r)
Substituting the given values:
n = log((31,300 * 0.03225) / (726.56 * 0.03225 + 31,300)) / log(1 + 0.03225)
Using a calculator or software, we find that n ≈ 9.989.
Therefore, we need approximately 10 deposits to reach a balance of $31,300 four years after the last deposit.
To know more about annual rate click here
brainly.com/question/6026546
#SPJ4
How many disks are in the bag of each colour? Can anyone explain how i should do B?

Answers
Answer:
10 red disks, 12 blue disks, 3 green disks
Step-by-step explanation:
a)
experimental probability = frequency / total amount of tries
experimental prob. of red = 20 / 50
b)
find the experimental probability of each disk
20/50 x 25 = red disks
20/50 x 25 = 10
-
24/50 x 25 = blue disks
24/50 x 25 = 12
-
6/50 x 25 = green disks
6 / 50 x 25 = 3
-
Hope this makes sense!
- profparis
A researcher wanted to estimate the mean number of hours adults spend formally exercising each week. She gathered a random sample and created a 95% confidence interval of (0.45 hours, 7.94 hours). Which of the following is the correct interpretation of this confidence interval?
Select one: O a. Weare 95% confident that the population mean number of hours adults spend on formal exercise each week lies between 0.45 and 7.94.
O b. There is a 0.95 probability that adults exercise formally between 0.45 hours and 7.94 hours per week.
O c. The sample mean number of hours adults spend on formal exercise each week lies between 0.45 and 7.94.
O d. The population mean number of hours adults spend on formal exercise each week lies between 0.45 and 7.94.
O e. We are 95% confident that the sample mean number of hours adults spend on formal exercise each week lies between 0.45 and 7.94.
Answers
The correct interpretation of the given confidence interval is: “We are 95% confident that the population mean number of hours adults spend on formal exercise each week lies between 0.45 and 7.94.”
Option (a) is the correct interpretation because a confidence interval provides an estimate of the range within which the true population parameter (in this case, the mean number of hours spent on formal exercise) is likely to fall. The confidence level of 95% indicates that if we were to repeat the sampling process and construct confidence intervals, 95% of those intervals would contain the true population mean.
Therefore, we can say with 95% confidence that the population mean lies within the interval (0.45 hours, 7.94 hours). Option (b) is incorrect because probabilities are not associated with confidence intervals. Options (c) and € refer to the sample mean, not the population mean. Option (d) incorrectly suggests that we know the true population mean is within the interval, whereas the confidence interval provides an estimate of the likely range.
Learn more about Population mean here: brainly.com/question/33543874
#SPJ11
If you draw a card with a value of three or less from a standard deck of cards, I will pay you $43, If not, you pay me $11 (Aces are considered the highest card in the deck.) Step 1 of 2 : Find the expected value of the proposition. Round your answer to two decimal places. Losses must be expressed as negative values
Answers
Answer:
$1.46
Step-by-step explanation:
Required cards for winning :
1's, 2's and 3's
There are 4 cards of each in a total of 52 cards ;
Therefore, number of winning cards ;
(4 * 3) = 12 cards
Hence,
P(winning) = 12 / 52 = 3 / 13
P(not winning) = 1 - 3 /13 = (13 - 3) / 13 = 10/13
Earning (X)
Amount earned for winning = $43
Amount lost for not winning = $11
X ___ $43 ______ - $11
P(X) _ 3/13 _______ 10/13
Expected value, E(X) = ΣX*P(X)
Σ(X) = (43 * 3/13) + (-11 * 10/13)
E(X) = 9.9230769 - 8.4615384
E(X) = 1.4615385
E(X) = $1.46
Sketch and label triangle ABC where A = 20°, B = 80°, c = 13 cm. Solve the triangle to find all missing measurements, rounding all results to the nearest whole number.
Answers
After solving the triangle we have the measurements as angles A = 20°, B = 80°, C = 80° and length of the sides as a ≈ 5 cm, b ≈ 13 cm, c = 13 cm
.
To sketch and solve triangle ABC, where A = 20°, B = 80°, and c = 13 cm, we start by drawing a triangle and labeling the given angle and side.
Sketching the Triangle:
Start by drawing a triangle. Label one of the angles as A (20°), another angle as B (80°), and the side opposite angle B as c (13 cm). Ensure the triangle is drawn to scale.
Solving the Triangle:
To find the missing measurements, we can use the Law of Sines and the fact that the sum of angles in a triangle is 180°.
a) Finding angle C:
Since the sum of angles in a triangle is 180°, we can find angle C:
C = 180° - A - B
C = 180° - 20° - 80°
C = 80°
b) Finding side a:
Using the Law of Sines:
a / sin(A) = c / sin(C)
a / sin(20°) = 13 / sin(80°)
a ≈ 5 cm (rounded to the nearest whole number)
c) Finding side b:
Using the Law of Sines:
b / sin(B) = c / sin(C)
b / sin(80°) = 13 / sin(80°)
b ≈ 13 cm (rounded to the nearest whole number)
Now we have the measurements of the triangle:
A = 20°, B = 80°, C = 80°
a ≈ 5 cm, b ≈ 13 cm, c = 13 cm
LEARN MORE ABOUT triangle here: brainly.com/question/31240589
#SPJ11
the balance in Ana's savings account may be modeled by the linear function y =50x + 2500, where x represents the number of months the have passed and y represents the account balance. Based on this function which of these is the best prediction of Ana's total savings after 3 years?
A. $2,650
B. $3,700
C. $4,300
D. $7,650
Answers
Answer:
C. $4,300
Step-by-step explanation:
3 years = 36 months so,
50(36) + 2500 = $4300
All 136 students in the Math Club went on a field trip. Some students rode in cars which hold 4
students each and some students rode in buses which hold 30 students each. How many of each type
of vehicle did they use if there were 8 vehicles total?
Answers
Answer:
They used 4 buses and 4 cars
Step-by-step explanation:
136/30= 4.5 (which means we can full 4 buses)
If we fill 4 buses : 4x30=120
We have 4 vehicles left and 16 students left too.
4x4= 16
We can fit every studens in the cars.
will mark branliest
Which graph shows the circle whose equation is (x−1)2+(y+3)2=16?

Answers
Which graph shows the circle whose equation is (x−1)2+(y+3)2=16?
circle formula:
\((x-h)^{2} +(y-k)^{2} =r^{2}\)
Given:
\((x-1)^{2} +(y+3)^{2} =4^{2}\)
put into circle formal format:
\((x-h)^{2} +(y-k)^{2} =r^{2}\\(x-1)^{2} +(y-(-3))^{2} =4^{2}\)
The center of the circle is at point (h,k)
\((x-1)^{2} +(y+3)^{2} =4^{2}\)
center should be at: (1,-3)
Answer:
lower row, left grid.
Answer:
Lower left, bottm, circle
Step-by-step explanation:
See attached graph

if possible can you include your method? :)

Answers
Step-by-step explanation:
11/15 = 73.333/100
73.333/100 = 0.73333
0.73333 = 0.73 (2sf/2dp)
Answer:
73/100
Step-by-step explanation
Since 0.73 =11/15 is false, there is no solution.
No solution
0.73 is the same as 73/100
so the answer is
73/100
in decimal form is 0.73
Find the product of (4 x 106) and (2 x 106). write the final answer in scientific notation. 8 x 106 8 x 1012 8 x 10012 8 x 1036
Answers
The product of (4 x 10⁶) × (2 x 10⁶) is 8 × 10⁶.
What is scientific notation?Scientific notation is similar to shorthand for writing extremely large or extremely small numbers. Rather than writing a number in decimal form, it is reduced to a number multiplied by ten.
The "coefficient" is the first number with in mathematical equation. The coefficient has to be greater than one and less than ten. The coefficient for creating scientific notation for number 256, for example, is 2.56.The second number as in equation is a power of ten, written as a power of ten with an exponent, such as 10², which stands for 10 x 10.Now, as per the given question;
The product of the given two number are-
= (4 x 10⁶) × (2 x 10⁶)
= 8 × 10⁶
Therefore, the scientific notation of the product of the give two numbers is 8 × 10⁶.
To know more about scientific notation, here
https://brainly.com/question/1767229
#SPJ4
The correct question is-
Find the product of (4 x 10⁶) and (2 x 10⁶). write the final answer in scientific notation. write the final answer in scientific notation.
Principal $1200Interest rate 6%Date borrowed May 15thDate repaid Aug 17thExact time ?Interest ?Maturity value ?

Answers
Given:
\(\begin{gathered} \text{ Principal}(p)=\text{\$}1200 \\ \text{ Interest rate}(r)=6\% \end{gathered}\)The date of borrowed is May 15th and the date of repayment is August 17th.
Required:
We have to find the exact time, interest, and maturity value.
Explanation:
The exact time between 15th May to 17th August is
\(t=94\text{ days.}\)Therefore the time given is
\(=\frac{94}{365}\text{ years.}\)We know that the formula to find the interest is
\(\text{ Interest}(I)=\frac{principal\times time\times interest\text{ rate}}{100}\)\(\Rightarrow I=\frac{p\times t\times r}{100}\)Therefore, the interest is
\(\begin{gathered} I=\frac{1200\times\frac{94}{365}\times6}{100} \\ \\ I=\frac{1200\times94\times6}{100\times365} \end{gathered}\)\(\begin{gathered} =\frac{12\times94\times6}{365} \\ \\ =\text{ \$}18.54 \end{gathered}\)Therefore, the maturity value is
\(\begin{gathered} =1200+18.54 \\ =\text{ \$}1218.54 \end{gathered}\)Final answer:
Hence the final answer is
\(\begin{gathered} \text{ exact time}=94\text{ days} \\ \text{ Interest}=\text{\$}18.54 \\ \text{ Maturity value}=\text{\$}1218.54 \end{gathered}\)Help!!! Bo and Erica are yoga instructors. Between the two of them, they teach 46 yoga classes each week. If Erica teaches 14 fewer than twice as many as Bo, how many classes does each instructor teach per week?
A.
22 Bo; 24 Erica
B.
24 Bo; 22 Erica
C.
17 Bo; 29 Erica
D.
20 Bo; 26 Erica
Answers
Answer: D
Step-by-step explanation:
2x - 14 + x= 46
3x = 60
x= 20
What is the domain of the function shown in the graph below?
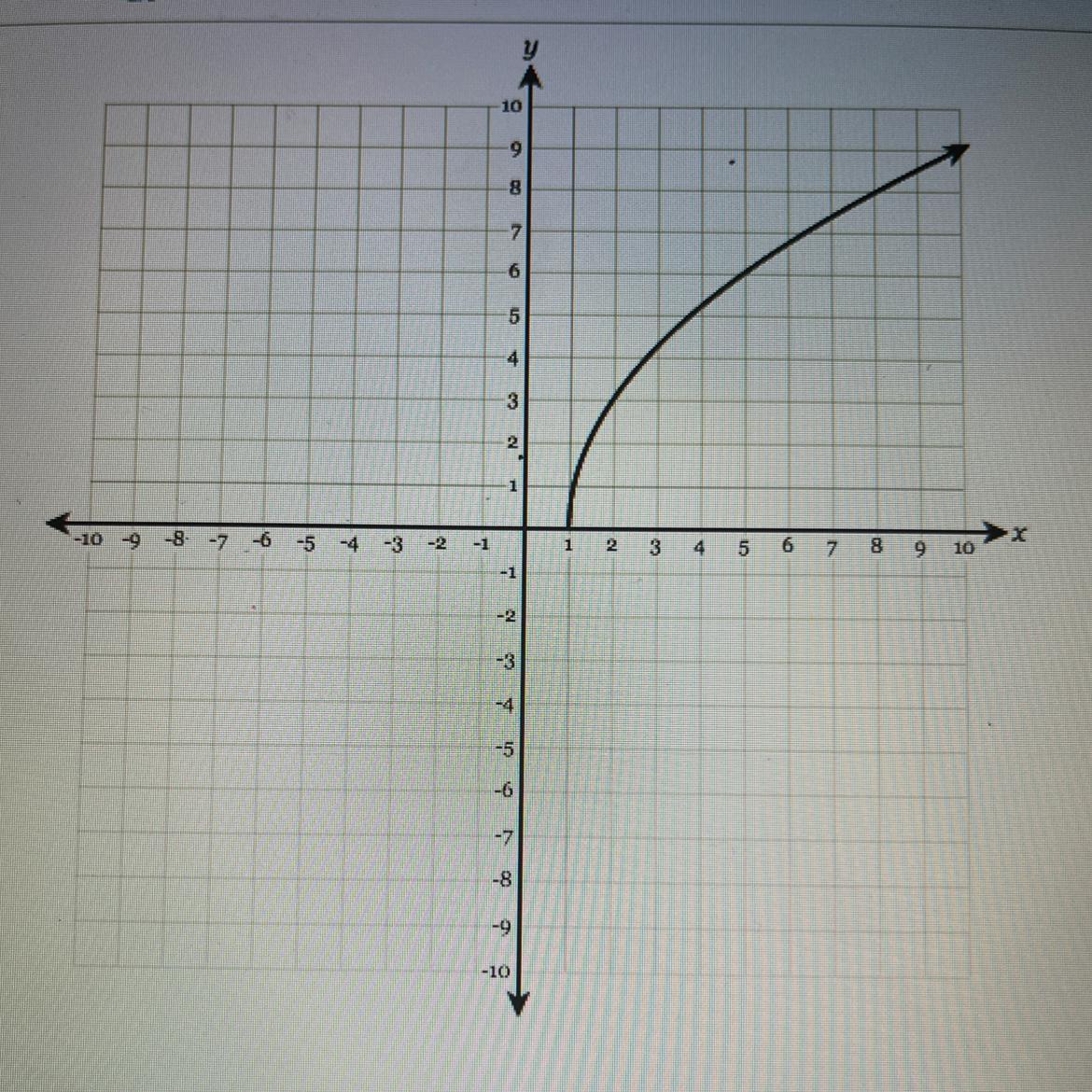
Answers
[1, oo)
domain = left to right
[where the point started and where it ends]
I really need help if anyone can help me plz help me right away

Answers
Answer:
C. g(x) = 4x²
Step-by-step explanation:
The function g(x) has a point (1,4) on its graph
Just plug in the values of x and y and see which of the options correct
A..............
g(x) =(4x)²4 = (4*1)²4 = 16Incorrect
B..............
g(x) = 1/4x²4 = 1/4*1²4 = 1/4Incorrect
C...............
g(x) = 4x²4 = 4*1²4 = 4Correct
D..............
g(x) = 16x²4 = 16*1²4 = 16Incorrect
A student makes the claim that 4x^2 - 81 = (x + 9)(x - 9) is a polynomial identity.
Which of the following statements is a correct analysis of the student's claim?

Answers
The student's claim is incorrect because , ( x + 9 ) ( x - 9 ) = x² - 81 , therefore the right side of the equation does not equal to the left side of the equation
Given data ,
Let the polynomial equation be represented as A
Now , the value of A is
A = ( x + 9 ) ( x - 9 )
On simplifying , we get
A = ( x + 9 ) ( x ) - ( x + 9 ) ( -9 )
A = x² + 9x - 9x - 81
On further simplification , we get
A = x² - 81
Hence , the equation is solved and A = x² - 81
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
Product of 1.25 (40)
Answers
Answer:
50
Step-by-step explanation:
1.25 (40) = 50
Please help on how to solve this

Answers
Answer:
11,73 cm (round to the nearest hundredths) ; 112 degrees
Step-by-step explanation:
circumference = 2 x radius x π = 2 x 6 x π = 37,699112 cm
measure of the arc =
37,699112 : 360 = x : 112
x = (112 * 37,699112)/360 = 11,728613 cm
the measure of the angle is given = 112 degrees
QUESTION 3 The initial value problem y' = √²-9. y(x)=yo has a unique solution guaranteed by Theorem 1.1 if Select the correct answer. O a.y=4 O b. yo = 1 Oc. yo=0 O d. yo = -3 O e. yo = 3 QUESTION 5 The solution of (x-2y)dx+ydy=0 is Select the correct answer. Oa. In 2 y+x MC X O b. lnx +In(y-x)=c Oc. In(-x) = -x O d. it cannot be solved ○e.In (-x)-y-x The solution of the differential equation y'+y=x is Select the correct answer. O a.y=-x-1+ce² Ob.y=x-1+cent Ocy=²0² Od.y=x-1+ce² Oe.
Answers
For question 3, the unique solution is guaranteed if yo = 3. For question 5, the solution is lnx + In(y-x) = c. For the last question, the solution is y = x - 1 + ce^(-x).
For question 3, the initial value problem y' = √(x²-9), y(x) = yo has a unique solution guaranteed by Theorem 1.1 if yo = 3. The reason is that the square root expression inside the differential equation is only defined when x²-9 is non-negative. Since the square root of a negative number is undefined in the real number system, yo cannot be any value that results in x²-9 being negative. Therefore, yo = 3 is the only valid choice.
For question 5, the given differential equation (x-2y)dx + ydy = 0 can be solved by integrating. By integrating the left-hand side of the equation, we obtain the solution lnx + In(y-x) = c, where c is the constant of integration. This is the correct answer (b).
For the last question, the differential equation y' + y = x can be solved using the method of integrating factors. Multiplying both sides of the equation by e^x, we get e^x * y' + e^x * y = xe^x. The left-hand side can be rewritten as (e^x * y)' = xe^x. Integrating both sides with respect to x, we have e^x * y = ∫xe^xdx = x * e^x - e^x + c. Dividing both sides by e^x, we get y = x - 1 + ce^(-x). Therefore, the correct answer is (b), y = x - 1 + ce^(-x).
To learn more about integration click here
brainly.com/question/31744185
#SPJ11
Question 4
What is the y-intercept of the line?
1
-2
1/2
0

Answers
Answer:
2.1
Step-by-step explanation:
The point at which the y axis is passed through is (0,1).
You buy 3.17 pounds of grapes, 1.45 pounds of pears, and 2.26 pounds of apples. What is you total bill
Answers
We buy:
• 3.17 pounds of grapes,
,• 1.45 pounds of pears,
,• 2.26 pounds of apples.
The total bill is just the sum of the money spent on each product:
Total bill = 3.17 pounds + 1.45 pounds + 2.26 pounds = 6.88 pounds.
Answer
The total bill is 6.88 pounds.
The clock shows the time that Ron left his home in the morning. He came home 7
hours and 35 minutes later. What time did Ron come home?
Answers
Answer: 14:35 hrs
Step-by-step explanation:
Missing time that Ron left was 07:00 hrs
Ron left the house at 07:00 hrs. If he arrived back to the house 7 hours and 35 minutes later, you can find out what time he arrived by simply adding the time he left to the time he stayed outside:
= 7 + 7hrs 35 minutes
= 14 hrs 35 minutes
= 14:35 hrs
Which is a composite number 37 or 29 or 43 or 21
Answers
Answer:
29
Step-by-step explanation:
It has more than 2 factors.
Which of the following correctly sets up the point-slope equation for this line?
y−7=13(x+6)y-7=\frac{1}{3}\left ( x+6 \right )y−7=
3
1
(x+6)
y+7=13(x+6)y+7=\frac{1}{3}(x+6)y+7=
3
1
(x+6)y+7=13(x+6)y+7=\frac{1}{3}(x+6)y+7=
3
1
(x+6)
y+7=13(x−6)y+7=\frac{1}{3}(x-6)y+7=
3
1
(x−6)
y−7=13(x−6)y-7=\frac{1}{3}(x-6)y−7=
3
1
(x−6)

Answers
Answer: \(y + 7 = \frac{1}{3}(x - 6)\\\\\)
Work Shown:
\(y - y_1 = m(x - x_1)\\\\y - (-7) = \frac{1}{3}(x - 6)\\\\y + 7 = \frac{1}{3}(x - 6)\\\\\)
