Triangle A′B′C′ is a dilation of triangle ABC about point P with a scale factor of 1/2. Is the dilation a reduction or an enlargement? reduction enlargement
Answers
Triangle A′B′C′ is a dilation of triangle ABC about point P with a scale factor of 1/2. The dilation is a reduction.
A dilation is a transformation that changes the size of a figure, but not its shape. It can be either an enlargement or a reduction depending on the value of the scale factor.
If the scale factor is greater than 1, then the image will be larger than the original figure. This is called an enlargement.
If the scale factor is between 0 and 1, then the image will be smaller than the original figure. This is called a reduction.
In this case, the scale factor is 1/2, which is less than 1. Therefore, the image of triangle ABC is smaller than the original triangle, and the dilation is a reduction.
Learn more about dilation at https://brainly.com/question/31009907
#SPJ11
Related Questions
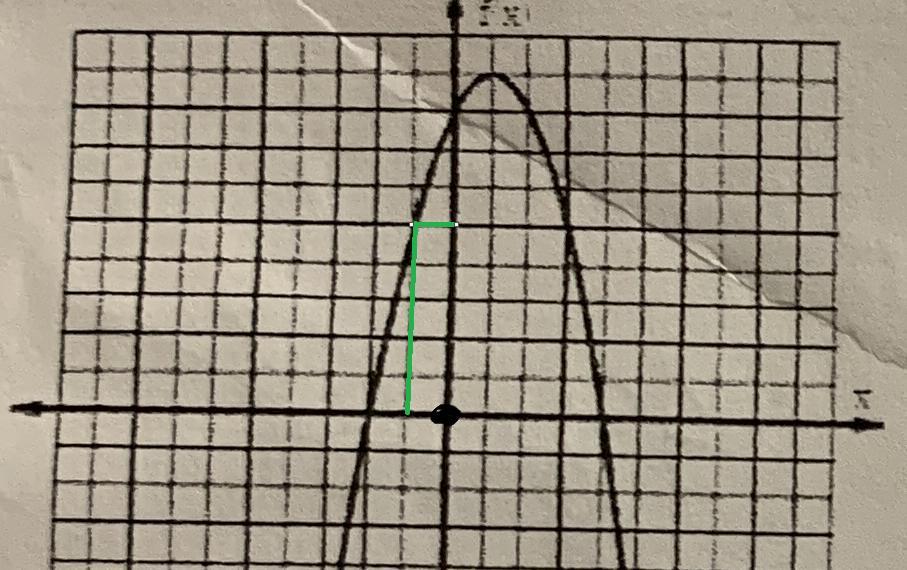
24. Find fl-1).For questions 24-27, use the graph below.25. Find f(4).26. Find f(-3).27. If f(x) = 9, find x.

Answers
Let's start by calculating the value for f(-1).
For this we go to the graph and count the number of squares to the left of the axis to be at -1. In this case f(-1) would be 5.
Now let's calculate f(4)
For this case the value of f(4) would be 0.
Similarly we calculate f(-3). As you can see in the graph it would be 6.
The last scenario would be for when f(x) = 9, we look for that value on the curve and realize that it corresponds to x = 1.



4t = 44 I just need help on what to do
Answers
Answer:
t is 11
Step-by-step explanation:
you divide each side by 4 to get rid of the coefficient on t and since theres
no equation left on either side you're left with t=11
Answer:
t = 11
Step-by-step explanation:
ima help explain it to you
Step one since the prime/first number is 4 put 4 as a denominator under both 4 and 44. That is the first step to these equations
Now, you have 4/4 and 44/4 if you divide 4 and 44 you will get 11. If you divide 4 and 4 you will get 1. equally you have 11/1 aka 11.
A EZ STEP IS TO LITTERALLY DIVDE 44 AND 4 RIGHT WHEN U SEE IT LOL
hope this helps!!
-Bacon
Solve each equation. log 5x+1=-1
Answers
Answer:
\(5x = - 1 - 1 = 5x \div 5 = - 2 \div 5 = 2 \div 5\)
If the mean is greater than the median, the data is likely: Group of answer choices Symmetric Normally distributed Left-skewed Right-skewed
Answers
If the mean is greater than the median, the data is likely Right-skewed.
In mathematics, the mean is the average of a set of data, which is calculated by adding all the numbers together and then dividing the result by the total number of numbers. Right-skewed distributions have long right tails and are characterized by having a mean that is greater than the median. There are two different sorts of means that may be calculated: the arithmetic mean and the geometric mean. The arithmetic mean is calculated by adding all of the numbers in a set and dividing by the total number of integers in the set.
Therefore, the answer is right-skewed. A data set that is skewed to the right is one where the tail to the right of the data clusters is longer than the tail to the left of the data clusters. This means that the data set will have a mean value that is greater than the median.
Learn more on mean here:
brainly.com/question/31101410
#SPJ11
i need help someone plzzz
Answers
Answer:
on what...like brush how do we help u if u don't have a question
Carlisle Transport had $4,520 cash at the beginning of the period. During the period, the firm collected $1,654 in receivables, paid $1,961 to supplier, had credit sales of $6,916, and incurred cash expenses of $500. What was the cash balance at the end of the period?
Answers
To calculate the cash balance at the end of the period, we need to consider the cash inflows and outflows.
Starting cash balance: $4,520
Cash inflows: $1,654 (receivables collected)
Cash outflows: $1,961 (payments to suppliers) + $500 (cash expenses)
Total cash inflows: $1,654
Total cash outflows: $1,961 + $500 = $2,461
To calculate the cash balance at the end of the period, we subtract the total cash outflows from the starting cash balance and add the total cash inflows:
Cash balance at the end of the period = Starting cash balance + Total cash inflows - Total cash outflows
Cash balance at the end of the period = $4,520 + $1,654 - $2,461
Cash balance at the end of the period = $4,520 - $807
Cash balance at the end of the period = $3,713
Therefore, the cash balance at the end of the period is $3,713.
To learn more about cash : brainly.com/question/31754110
#SPJ11
How do i find area of a rectangle
Answers
Answer: find an alength times a weight
Step-by-step explanation:
What is the Area of a Rectangle?
a Definition: The area of the rectangle is the region occupied by a rectangle within its four sides or boundaries.
The area of a rectangle depends on its sides. The formula for area is equal to the product of the length and breadth of the rectangle. Whereas when we speak about the perimeter of a rectangle, it is equal to the sum of all its four sides. Hence, we can say, the region enclosed by the perimeter of the rectangle is its area. But in the case of a square, since all the sides are equal, therefore, the size of the court will be equal to the court of side length.
the
1. Find the length of the rectangle. In most cases, you will be given the length; if not, you can find it using a ruler.
Note that the double hash marks on the long sides of the rectangle mean that the lengths of the two sides are the same.
2. Find the width of the rectangle. Use the same methods to find it.
Note that the single hash marks on the wide sides of the rectangle mean that the two widths have equal lengths.
3. Write the length and width next to each other. In this example, the length is 5 cm and the width is 4 cm.
4. Multiply the length times the width. Your length is 5 cm and your width is 4 cm, so you should plug them into the equation A = L * W to find the area.
A = 4 cm * 5 cm
A = 20 cm^2
5. State your answer in square units. Your final answer is 20 cm^2, which means "twenty centimeters squared.
You can write your final answer in one of two ways: either 20 cm. sq. or 20 cm^2.
What is equivalent to 3x – 2y = 4?
Answers
Answer:
This equation is equal to y=3/2x-2
Step-by-step explanation:
a careless university student leaves her iclicker device behind with probability 1/4 each time she attends a class. she sets out with her iclicker device to attend 5 different classes (each class is in a different lecture theatre). part 1) if she arrives home without her iclicker device and she is sure she has the iclicker device after leaving the first class, what is the probability (to 3 significant figures) that she left it in the 5th class? probability
Answers
The probability of leaving it in any given class is 1/4, the probability of leaving it in the 5th class is 1/4, or\(0.250 (25.0%).\)
The probability that the student left her iClicker device in the 5th class is 0.250 (25.0%). This is because the probability of leaving it in any given class is 1/4, and as she attends 5 different classes,
there is 5/4 or 1.25 chances of her leaving it in the 5th class.
To explain further, the probability of an event can be calculated by dividing the number of ways the event can occur by the total number of possible outcomes. In this case, the event is leaving the iClicker device in the 5th class, and the total number of possible outcomes is 5 (for the 5 classes).
for such more questions on probability
https://brainly.com/question/24756209
#SPJ11
What is your hypothesis from the activity in the lesson? Will the shorter cylinder or taller cylinder have the larger volume? Or, will both cylinders have the same volume? Explain your reasoning using complete sentences. [Note: There is no wrong answer as long as you make a hypothesis and explain your reasoning using complete sentences.]
Answers
Answer:
Taller because it is bigger and more likely to have greater volume
Step-by-step explanation:
its correct 100%
The correct statement is,
''The taller cylinder have the larger volume than shorter cylinder.''
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
Will the shorter cylinder or taller cylinder have the larger volume.
Since, We know that;
The volume of a cylinder is calculated by multiplying the area of the base by the height.
And, since the height of the taller cylinder is greater than the shorter cylinder, it is likely to have a larger volume.
Thus, The taller cylinder have the larger volume than shorter cylinder.
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ3
Please solve all of it

Answers
Answer:
a=f/3
b=8or it g
gf/3
c=-3gx*2
bonus=f(x)=h(−4x)
Step-by-step explanation:
Solve for x. Round your answer to the nearest tenth if necessary. NO SCAMS OR LINKS PLEASE!!!!!! ANSWER IS NOT 14.1

Answers
Answer:
\(\boxed {\boxed {\sf x\approx 7.3}}\)
Step-by-step explanation:
The triangle has a small square in the corner representing a 90 degree angle. This is a right triangle so we can use the Pythagorean Theorem to solve for the sides.
\(a^2+b^2=c^2\)
In this equation, a and b are the legs and c is the hypotenuse.
x and 8.5 are the legs because they make up the right angle. 11.2 is the hypotenuse because it is opposite the right angle.
a= xb=8.5 c=11.2Substitute the values into the formula.
\(x^2+(8.5)^2=(11.2)^2\)
Solve the exponents.
(8.5)²= 8.5*8.5= 72.25 (11.2)²= 11.2*11.2= 125.44\(x^2+72.25 =125.44\)
Solve for x by isolating the variable. 72.25 is being added, so we subtract 72.25 from both sides because subtraction is the inverse operation of addition.
\(x^2+72.25-72.25 = 125.44-72.25\)
\(x^2=125.44-72.25\)
\(x^2=53.19\)
x is being squared, so we take the square root of both sides.
\(\sqrt{x^2}=\sqrt {53.19}\)
\(x=\sqrt{53.19\)
\(x=7.29314746869\)
Round to the nearest tenth. The 9 in the hundredth place tells us to round the 2 up to a 3.
\(x \approx 7.3\)
The unknown side, x, is approximately 7.3
Wally is employed as an executive with Pay More Incorporated. To entice Wally to work for Pay More, the corporation loaned him $20,000 at the beginning of the year at a simple interest rate of 1 percent. Wally would have paid interest of $2,400 this year if the interest rate on the loan had been set at the prevailing federal interest rate.b. Assume instead that Pay More forgave the loan and interest on December 31. What amount of gross income does Wally recognize this year?
Answers
Answer:18000$
Step-by-step explanation:
What’s the measure of the other angle?

Answers
Which graph represents a function

Answers
Answer:
c
Step-by-step explanation:
it moves virticly across
make t the subject formula h=square root of 2t-3
Answers
h^2 = 2t - 3
2t = h^2 + 3
t = (h^2 + 3)/2
The subject formula for t in equation form is "t = (h² + 3)/2".
What is the equation?The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions.
Given, the subject formula h=square root of 2t-3
Since h = √2t-3
thus solving the equation for t
h² = 2t - 3
2t = h² + 3
t = (h² + 3)/2
Therefore, the Simplified form of the given equation in the terms of t is "t = (h² + 3)/2"
Learn more about equations here:
https://brainly.com/question/29657983
#SPJ2
12d^2 + 3dx + x
- (-4d^2 + 2dx - 8x)
Answers
Answer:
dx+9x+16d^2 dont know it it helps any but i tried
Step-by-step explanation:
a) Work out the minimum number of dogs that could have a mass of more than 24 kg
. b) Work out the maximum number of dogs that could have a mass of more than 24 kg. Mass, z (kg)

Answers
Answer:
......................
Which of the following could be an example of a function with a domain
(-∞0,00) and a range (-∞,4)? Check all that apply.
A. V = -(0.25)* - 4
-
□ B. V = − (0.25)*+4
c. V = (3)* +4
□ D. V = − (3)* — 4
-

Answers
The correct options that could be an example of a function with a domain (-∞0,00) and a range (-∞,4) are given below.Option A. V = -(0.25)x - 4 Option B. V = − (0.25)x+4
A function can be defined as a special relation where each input has exactly one output. The set of values that a function takes as input is known as the domain of the function. The set of all output values that are obtained by evaluating a function is known as the range of the function.
From the given options, only option A and option B are the functions that satisfy the condition.Both of the options are linear equations and graph of linear equation is always a straight line. By solving both of the given options, we will get the range as (-∞, 4) and domain as (-∞, 0).Hence, the correct options that could be an example of a function with a domain (-∞0,00) and a range (-∞,4) are option A and option B.
Know more about function here:
https://brainly.com/question/11624077
#SPJ8
While reviewing the previous day’s arrest report, a police sergeant notices that six suspects were arrested, all of whom had either one or two previous arrests. Including yesterday’s arrests, there were 16 total arrests among them. How many suspects had less than two prior arrests?
There were __ suspects that had less than two prior arrests
Answers
There were no suspects with less than two prior arrests in this scenario.
Let's solve the problem step by step:
Let's assume the number of suspects with one prior arrest is "x" and the number of suspects with two prior arrests is "y".
According to the given information:
The total number of suspects is 6.
So, x + y = 6 -- (Equation 1)
The total number of arrests, including yesterday's arrests, is 16.
The number of arrests for suspects with one prior arrest is x + 1 (yesterday's arrest plus their one prior arrest).
The number of arrests for suspects with two prior arrests is 2y (yesterday's arrest plus their two prior arrests).
So, (x + 1) + 2y = 16 -- (Equation 2)
Now, we have a system of two equations (Equation 1 and Equation 2) that we can solve to find the values of x and y.
Solving the equations:
From Equation 1, we can rewrite it as x = 6 - y and substitute it into Equation 2:
(6 - y + 1) + 2y = 16
7 - y + 2y = 16
y + 7 = 16
y = 16 - 7
y = 9
Now, substitute the value of y back into Equation 1 to find x:
x = 6 - y
x = 6 - 9
x = -3
Since we cannot have a negative number of suspects, we conclude that there was an error in the given information or calculations.
Therefore, there were no suspects with less than two prior arrests in this scenario.
Learn more about scenario here
https://brainly.com/question/29445672
#SPJ11
"Derive the demand function
Endowment (1,0)
U(x,y) = -e⁻ˣ — e⁻ʸ
Answers
To derive the demand function from the given utility function and endowment, we need to determine the optimal allocation of goods that maximizes utility. The utility function is U(x, y) = -e^(-x) - e^(-y), and the initial endowment is (1, 0).
To derive the demand function, we need to find the optimal allocation of goods x and y that maximizes the given utility function while satisfying the endowment constraint. We can start by setting up the consumer's problem as a utility maximization subject to the budget constraint. In this case, since there is no price information provided, we assume the goods are not priced and the consumer can freely allocate them.
The consumer's problem can be stated as follows:
Maximize U(x, y) = -e^(-x) - e^(-y) subject to x + y = 1.
To solve this problem, we can use the Lagrangian method. We construct the Lagrangian function L(x, y, λ) = -e^(-x) - e^(-y) + λ(1 - x - y), where λ is the Lagrange multiplier.
Taking partial derivatives of L with respect to x, y, and λ, and setting them equal to zero, we can find the values of x, y, and λ that satisfy the optimality conditions. Solving the equations, we find that x = 1/2, y = 1/2, and λ = 1. These values represent the optimal allocation of goods that maximizes utility given the endowment.
Therefore, the demand function derived from the utility function and endowment is x = 1/2 and y = 1/2. This indicates that the consumer will allocate half of the endowment to each good, resulting in an equal distribution.
Learn more about partial derivatives here: brainly.com/question/32624385
#SPJ11
The mean time required to repair breakdowns of a certain copying machine is 93 minutes. The company which manufactures the machines claims that breakdowns of its newer model are easier to fix. To test this claim, a sample of 18 breakdowns of the new model were observed, resulting in a mean repair time of 86.8 minutes with a standard deviation of 14.6 minutes. Using a significance level of a = 0.10, determine if the new copy machines are faster to repair. State clearly what your null and alternative hypotheses are, show your work, and state your conclusion.
Answers
A significance level of 0.10, we have enough evidence to conclude that the new copy machines have a significantly faster mean repair time compared to the older model.
To test if the new copy machines are faster to repair, we can set up the following null and alternative hypotheses:
Null Hypothesis (H₀): The mean repair time for the new copy machines is the same as the mean repair time for the older model.
Alternative Hypothesis (H₁): The mean repair time for the new copy machines is less than the mean repair time for the older model.
Let's perform a one-sample t-test to test these hypotheses. The test statistic is calculated as:
t = (sample mean - population mean) / (sample standard deviation / √(sample size))
Given:
Population mean (μ) = 93 minutes
Sample mean (\(\bar x\)) = 86.8 minutes
Sample standard deviation (s) = 14.6 minutes
Sample size (n) = 18
Significance level (α) = 0.10
Calculating the test statistic:
t = (86.8 - 93) / (14.6 / sqrt(18))
t = -6.2 / (14.6 / 4.24264)
t ≈ -2.677
The degrees of freedom for this test is n - 1 = 18 - 1 = 17.
Now, we need to determine the critical value for the t-distribution with 17 degrees of freedom and a one-tailed test at a significance level of 0.10. Consulting a t-table or using statistical software, the critical value is approximately -1.333.
Since the test statistic (t = -2.677) is less than the critical value (-1.333), we reject the null hypothesis.
To know more about significance level:
https://brainly.com/question/4599596
#SPJ4
log (x^2 – 5x + 14) = 2x + 4
Need an answer ASAP must be in exponential equation
Answers
Answer:
x=2 or x=5
Step-by-step explanation:
There are 16 girls and 20 boys in school band what is the ratio of girls to boys in simplest form
Answers
Answer:
4/5
Step-by-step explanation:
Since we know that the first ratio that we have is 16:20, all you have to do is simplify by dividing and you get 4/5.
There you go.
A STEAM tutoring center offers a robotics class and an app development class to its members. There are 280 members, all of which are registered for at least one class this spring. If 75% of members registered for a robotics class and 50% registered for an app development class, how many members registered for both robotics and app development?
Answers
The number of students who registered for both robotics and app development is 70.
What is a percentage?The percentage is calculated by dividing the required value by the total value and multiplying by 100.
Example:
Required percentage value = a
total value = b
Percentage = a/b x 100
Example:
50% = 50/100 = 1/2
25% = 25/100 = 1/4
20% = 20/100 = 1/5
10% = 10/100 = 1/10
We have,
Total members = 280
The number of members who registered for the robotics class.
= 75% of 280
= 3/4 x 280
= 3 x 70
= 210
The number of members who registered for the app development class
= 50% of 280
= 1/2 x 280
= 140
We see that,
210 + 140 = 350
But we have 280 members.
So,
The number of students who registered for both robotics and app development.
= 350 - 280
= 70
Thus,
The number of students who registered for both robotics and app development is 70.
Learn more about percentages here:
https://brainly.com/question/11403063
#SPJ1
While measuring a wire a 5cm wire, a construction worker measured it 5.2 cm by mistake. What is the percent error?
Answers
Answer:
4%
Step-by-step explanation:
Actual length of wire = 5 cm
The measured length of wire = 5.2 cm
We need to find the percent error in the measurement of the length of wire. It can be calculated as follows :
\(\%=\dfrac{\text{measured length-actiual length}}{\text{actual length}}\times 100\\\\=\dfrac{5.2-5}{5}\times 100\\\\=4\%\)
So, the required percent error is 4%.
Use the Laplace transform to solve the given initial-value problem. Use the table of Laplace transforms in Appendix III as needed. y' + y = t sin t, y(0) = 0
Answers
The solution to the given initial-value problem by using the Laplace transform is \(y(t) = e^{(-t) }- cos(t) + t sin(t) - t cos(t).\)
To solve the initial-value problem using Laplace transform, we'll first take the Laplace transform of both sides of the differential equation and use the initial condition to find the Laplace transform of the solution.
Taking the Laplace transform of the given differential equation, we have:
\(L{[y']} + L{[y]} = L{[t sin t]}\)
Applying the linearity property of the Laplace transform and using the derivative property \(L{[y']} = sY(s) - y(0)\), where Y(s) represents the Laplace transform of y(t), we get:
\(sY(s) - y(0) + Y(s) = L{[t sin t]}\)
Since y(0) = 0 according to the initial condition, the equation simplifies to:
\(sY(s) + Y(s) = L{[t sin t]}\)
Using the table of Laplace transforms, we find that the Laplace transform of t sin t is:
\(L{(t sin t)} = 2 / (s^2 + 1)^2\)
Substituting this into the equation, we have:
\(sY(s) + Y(s) = 2 / (s^2 + 1)^2\)
Now, we can solve this equation for Y(s):
\(Y(s)(s + 1) = 2 / (s^2 + 1)^2\)
Dividing both sides by (s + 1), we get:
Y(s) = 2 / ((s + 1)(s^2 + 1)^2)
\(Y(s) = 2 / ((s + 1)(s^2 + 1)^2)\)
Now, we need to find the inverse Laplace transform of Y(s) to obtain the solution y(t).
Using partial fraction decomposition, we can express Y(s) as:
\(Y(s) = A / (s + 1) + (Bs + C) / (s^2 + 1) + (Ds + E) / (s^2 + 1)^2\)
Solving for the constants A, B, C, D, and E, we can rewrite Y(s) as:
\(Y(s) = 1 / (s + 1) - (s + 1) / (s^2 + 1) + (2s - 1) / (s^2 + 1)^2\)
Taking the inverse Laplace transform, we find that the solution y(t) is:
\(y(t) = e^{(-t)} - cos(t) + t sin(t) - t cos(t)\)
Therefore, the solution to the given initial-value problem by using the Laplace transform is \(y(t) = e^{(-t) }- cos(t) + t sin(t) - t cos(t).\)
Learn more about Laplace transforms here:
https://brainly.com/question/31689149
#SPJ4
Prove
that BUGS is a trapezoid with coordinates B(-2,-1), U(0,3), G(3,2) and S(4,-3).
Answers
Answer:
Proved
Step-by-step explanation:
Given
\(B =(-2,-1)\)
\(U = (0,3)\)
\(G = (3,2)\)
\(S = (4,-3)\)
Required
Prove BUGS is a trapezoid
Given the coordinates, to prove a trapezoid; all we need to do is to check if one pair of sides is parallel.
Taking BU and GS as a pair
First, we calculate the slope using:
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
For BU
\(B =(-2,-1)\) --- \((x_1,y_1)\)
\(U = (0,3)\) --- \((x_2,y_2)\)
So, we have:
\(m = \frac{3 - -1}{0- -2}\)
\(m = \frac{4}{2}\)
\(m = 2\)
For GS
\(G = (3,2)\) --- \((x_1,y_1)\)
\(S = (4,-3)\) --- \((x_2,y_2)\)
So, we have:
\(m = \frac{-3-2}{4-3}\)
\(m = \frac{-5}{1}\)
\(m = -5\)
The slope of BU and GS are not the same; hence, they are not parallel.
Taking BS and GU as a pair
Calculate the slope
For BS
\(B =(-2,-1)\) --- \((x_1,y_1)\)
\(S = (4,-3)\) --- \((x_2,y_2)\)
So, we have:
\(m = \frac{-3 - -1}{4- -2}\)
\(m = \frac{-2}{6}\)
\(m = -\frac{1}{3}\)
For GU
\(G = (3,2)\) --- \((x_1,y_1)\)
\(U = (0,3)\) --- \((x_2,y_2)\)
So, we have:
\(m = \frac{3-2}{0-3}\)
\(m = \frac{1}{-3}\)
\(m = -\frac{1}{3}\)
The slope of BS and GU are the same; hence, they are parallel.
BUGS is a trapezoid because BS and GU have the same slope
Solve by factoring. Check your answers. x²=-x+6
Answers
The factoring of the expression x²=-x+6 is (x-2)(x+3)
By ordering the values, we get:
x² + x - 6 = 0
To solve this exercise, we have to follow the rules of factoring:
1. Looking for the a and b number that state the following equations:
a + b = 1a * b = - 6Analyzing that (a*b) is a negative number, it means that (a) and (b) have different signs, and due to the results of (a+b) is positive the higher number has to be the positive one.
The number could be:
a = -2
b = 3
Confirming:
a + b = -2 + 3 = 1
a * b = (-2) * 3 = - 6
2. Rewriting the factored expression (x+a)(x+b) with the obtained values, we get:
(x-2)(x+3)
What is factoring?Is a technique that consist of decomposition of a factor into a product of another factor, which when multiplied together give the original number.
Learn more about factoring at brainly.com/question/24734894
#SPJ4

Find a solution to this system of equations:
5x-3y=20
15x+6y=60
Write your solution in (x,y) form.
Please help!!!!!
Answers
Answer:
(x, y) = (4, 0)
Step-by-step explanation:
You want the solution to the system of equations ...
5x -3y = 2015x +6y = 60Standard formIt often works well to start the solution process by putting both equations into standard form. We do that by removing any common factors from the coefficients. Here, we see that the second equation's coefficients each have a factor of 3, so we can remove that and rewrite the system as ...
5x -3y = 205x +2y = 20ObservationChanging the coefficient of the y-term has no effect, telling us that y=0, and the equation reduces to ...
5x = 20
x = 4
More formally, if we subtract the first equation from the second, we get ...
(5x +2y) -(5x -3y) = (20) -(20)
5y = 0 . . . . . . simplify
y = 0 . . . . . . . divide by 5
The solution is (x, y) = (4, 0).
