To include the personal assets and transactions of a business's owner in the records and reports of the business would be in conflict with the
Answers
Answer:
Khgiqjdbdnekjfjwjehsio
Related Questions
2×1+1× 1/10 +5× 1/100 +5× 1/1000 =
Answers
Answer:
2.15500
Step-by-step explanation:
hope it's help
#MASTER GROUP
# FIRST MASTER
# PHILIPPINES

Which of the following is not a criteria for the construction of triangle ASA SSS AAA SAS?
Answers
Answer:
AAA
Step-by-step explanation:
There's no angle angle angle (AAA) because all triangle's angles add up to 180
6+754+537+633+632+11+98+2
Answers
Answer:
2673
Step-by-step explanation:
2673
I've lost my pen so I can't write it down on paper, sowwy
Does AAS prove congruence?
Answers
Yes, AAS proves congruence.
AAS stands for Angle-Angle-Side. When two angles and a non-included side of a triangle are equal to the corresponding angles and sides of another triangle, then the triangles are said to be congruent.
AAS congruence can be proved in easy steps.
Suppose we have two triangles ABC and DEF, where
∠B = ∠E [Corresponding angles] ∠C = ∠F [Corresponding angles] And
AC = DF [Adjacent sides]
By the angle sum property of the triangle, we know that;
∠A + ∠B + ∠C = 180 ………(1)
∠D + ∠E + ∠F = 180 ……….(2)
From equations 1 and 2 we can say;
∠A + ∠B + ∠C = ∠D + ∠E + ∠F
∠A + ∠E + ∠F = ∠D + ∠E + ∠F [Since, ∠B = ∠E and ∠C = ∠F] ∠A = ∠D
Hence, in triangles ABC and DEF,
∠A = ∠D
AC = DF
∠C = ∠F
Hence, by AAS congruency,
Δ ABC ≅ Δ DEF
To know more about congruent triangles visit: brainly.com/question/22062407
#SPJ4
PLZ HELP an apple juice container has a tiny hole in it so it is slowly leaking is the container leaks three ounces every 19 minutes how long will it take for 16 ounces of juice in the container to leak out?

Answers
Answer:
the answer is on line and it have the correct work
Find m/TRS if m/1 = 2x + 4 and
m/2= 3x - 3.
T
P
S
1
R

Answers
If the angles are ∠1 = 2x + 4 and ∠2 = 3x - 3, then m∠TRS = 36°.
What is an angle?
An angle is a figure in plane geometry that is created by two rays or lines that have a shared endpoint. The Latin word "angulus," which meaning "corner," is the source of the English term "angle." The shared terminus of two rays is known as the vertex, and the two rays are referred to as sides of an angle.
The measure of ∠1 = 2x + 4
The measure of ∠2 = 3x - 3
The measure of ∠TRS is -
∠TRS = ∠1 + ∠2
Since, PR is a bisector then ∠1 = ∠2.
The equation is -
2x + 4 = 3x - 3
2x - 3x = - 3 - 4
-x = -7
x = 7
Substitute the value of x in the angles -
∠1 = 2(7) + 4
∠1 = 14 + 4
∠1 = 18°
∠2 = 3(7) - 3
∠2 = 21 - 3
∠2 = 18°
So, the value of ∠TRS is -
∠1 + ∠2
18° + 18°
36°
Therefore, the measure of ∠TRS is 36°.
To learn more about angle from the given link
https://brainly.com/question/25716982
#SPJ1
−8tan 1+tan2x Use appropriate identities to rewrite the following expression in terms containing only first powers of sine
Answers
By using Pythagorean identities the expression can be written as
-8 (sin ( x ) + 1 -sin 2x)
The Pythagorean identity is an important identity in trigonometry derived from the Pythagorean theorem. These identities are used to solve many trigonometric problems where, given a trigonometric ratio, other ratios can be found. The basic Pythagorean identity, which gives the relationship between sin and cos, is the most commonly used Pythagorean identity:
sin2θ + cos2θ = 1 (gives the relationship between sin and cos)
There are two other Pythagorean identities as follows :
sec2θ - tan2θ = 1 (gives the relationship between sec and tan)
csc2θ - cot2θ = 1 (gives the relationship between csc and cot)
Given expression is:
-8tanx/ 1 +tan2x
we know that:
By the Pythagorean Theorem:
1 + tan²x = sec²x
and tan x = sin x/cos x
and, sec x = 1/cos x
Now, we can write as:
-8tanx / 1 +tan²x
= -8 tan x / sec²x
= -8 sin x /cos x ÷ 1/cos²x
= -8 sin x/cos x × cos²x/1
= -8 (sin ( x ) + 1 -sin 2x)
Complete Question:
Use appropriate identities to rewrite the following expression in terms containing only first powers of sine:
−8tan 1 + tan2x.
Learn more about Pythagorean identities
https://brainly.com/question/10285501
#SPJ4
(ASAPPPP!!!! POINTS INCLUDEDDDD!!!! ) An object attached to a spring oscillates around a position and is represented by the function y = 2 cos (x -0.02), with
time in a seconds. What is the maximum height of the object in inches, and how many times does the maximum occur on
the interval 0 < x < 20?
- 3times, 8inches
- 4times, 8inches
- 3times, 2inches
- 4times, 2inches
Answers
4times, 2inches occur on the interval 0 < x < 20
Find the maximum interval?y=2cos (x-0.02)(0<x<20)y max=2 inches-1<cos<1/-0.02<x<-0.02<1998when x - 0.02=0 2π 4 π4 times In mathematics, a interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers x satisfying 0 ≤ x ≤ 1 is an interval which contains 0, 1, and all numbers in betweenIntervals are written with rectangular brackets or parentheses, and two numbers delimited with a comma. The two numbers are called the endpoints of the interval. The number on the left denotes the least element or lower bound. The number on the right denotes the greatest element or upper bound.To learn more about interval refers to:
brainly.com/question/29004222
#SPJ1
Find a polynomial p(t) of degree 6 which has a zero of multiplicity 2 at t = 1 and a zero of multiplicity 3 at
t = 2, and also satisfying: p(0) = 2 and p`(0) = 1. What is the other root of p(t)?
Answers
The polynomial that satisfies the conditions is: p(t) = (1/4)(t - 1)² (t - 2)³
This polynomial has a root of multiplicity 2 at t = 1 and a root of multiplicity 3 at t = 2, and also satisfies p(0) = 2 and p'(0) = 1.
The other root of p(t) can be found by factoring the polynomial further, but since the degree of the polynomial is 6, it will have 3 additional roots, which can be found using various mathematical methods such as the Rational Root Theorem or numerical methods.
Polynomials are mathematical expressions that involve variables raised to a power and are combined using addition and subtraction operations. The degree of a polynomial is the highest power of the variable in the expression.
A zero of a polynomial is a value of the variable for which the polynomial evaluates to zero. The multiplicity of a zero is the number of times the factor (t - zero) appears in the polynomial's factorization.
Given the conditions that the polynomial p(t) has a zero of multiplicity 2 at t = 1 and a zero of multiplicity 3 at t = 2, we can write p(t) as the product of factors (t - 1)² and (t - 2)³:
p(t) = a(t - 1)² (t - 2)³
where a is some constant. To find the value of a, we use the fact that p(0) = 2 and p'(0) = 1. We evaluate p(0) and p'(0) using the polynomial expression above, then solve for a.
First, we find p(0):
p(0) = a(0 - 1)² (0 - 2)³ = a(-1)² (-2)³ = a * 8
Next, we find p'(0):
p'(t) = 2a(t - 1)(t - 2)³ + a(t - 1)² * 3(t - 2)²
p'(0) = 2a(-1)(-2)³ + a(-1)² * 3(-2)² = 16a + 12a = 28a
Now that we have expressions for p(0) and p'(0), we can solve for a:
p(0) = a * 8 = 2 => a = 1/4
p'(0) = 28a = 1 => 28 * 1/4 = 1
So the polynomial that satisfies the conditions is:
p(t) = (1/4)(t - 1)² (t - 2)³
Here you can learn more about Polynomials
https://brainly.com/question/11536910#
#SPJ11
volume of a cylinder is 1540 cm³ and the difference of its height and radius is 3 cm, then find the total surface area of the cylinder.
Answers
Answer:
Let's assume the height of the cylinder to be 'h' and its radius to be 'r'. We can use the given information to form two equations.
First, we know that the volume of the cylinder is 1540 cm³:
V = πr²h = 1540
Second, we know that the difference between the height and the radius is 3 cm:
h - r = 3
Using the second equation, we can solve for 'h' in terms of 'r':
h = r + 3
Substituting this into the first equation, we get:
πr²(r + 3) = 1540
Expanding the left side of the equation and simplifying, we get:
πr³ + 3πr² - 1540 = 0
We can solve for 'r' using the cubic formula, but it's easier to notice that 'r' must be close to 10. We can try different values of 'r' until we get an answer close to 1540. If we try 'r' = 10, we get:
π(10)²(10+3) = 3300π
So, the radius is approximately 10 cm and the height is approximately 13 cm.
To find the total surface area of the cylinder, we need to find the area of the top and bottom circles and the area of the curved surface. The area of each circle is πr², so the total area of the circles is:
2πr² = 200π cm²
The area of the curved surface is the circumference of the circle times the height of the cylinder, or 2πrh. Substituting the values of 'r' and 'h' that we found earlier, we get:
2π(10)(13) = 260π cm²
Therefore, the total surface area of the cylinder is:
200π + 260π = 460π ≈ 1442.4 cm²
So, the total surface area of the cylinder is approximately 1442.4 cm².
The graph of y=x3−6x2−58x+1 y = x 3 - 6 x 2 - 58 x + 1 has a
slope of 5 5 at two points. Find the coordinates of the points.
Enter the points in increasing order of x x -value.
Answers
The coordinates of the points where the graph of y = \(x^3\) - \(6x^2\) - 58x + 1 has a slope of 5 are (-3, -47) and (7, -153).
To find the coordinates of the points where the graph has a slope of 5, we need to determine the values of x for which the derivative of the function y = \(x^3 - 6x^2\) - 58x + 1 is equal to 5.
1. Find the derivative of the function:
The derivative of y = \(x^3 - 6x^2\) - 58x + 1 can be found by taking the derivative of each term separately:
dy/dx = \(3x^2\)- 12x - 58.
2. Set the derivative equal to 5:
Setting the derivative equal to 5 gives us the equation: \(3x^2\) - 12x - 58 = 5.
3. Rearrange the equation:
Rearranging the equation gives us: \(3x^2\) - 12x - 63 = 0.
4. Solve the quadratic equation:
We can solve the quadratic equation by factoring or using the quadratic formula. Factoring \(3x^2\) - 12x - 63 = 0 gives us (x - 7)(3x + 9) = 0.
Setting each factor equal to zero, we have two possible values for x:
x - 7 = 0 --> x = 7,
3x + 9 = 0 --> x = -3.
5. Find the corresponding y-values:
Substituting the x-values into the original function, we can find the corresponding y-values:
For x = -3, y = (-\(3)^3 - 6(-3)^2\) - 58(-3) + 1 = -47.
For x = 7, y = \(7^3 - 6(7)^2\) - 58(7) + 1 = -153.
Therefore, the coordinates of the points where the graph has a slope of 5 are (-3, -47) and (7, -153), in increasing order of x-value.
For more such questions on graph, click on:
https://brainly.com/question/19040584
#SPJ8
Assign smallest to the smallest number of students they should sample to ensure that a 95% confidence interval for the parameter has a width of no more than 6% from left end to right end.
Answers
To determine the smallest number of students to sample for a 95% confidence interval with a width of no more than 6%.
We need to consider the desired level of confidence and the desired margin of error.
Determine the margin of error: The margin of error is the maximum allowable distance from the sample estimate to the true parameter value. In this case, the width of the confidence interval is given as 6%, so the margin of error is half of that, which is 3%.
Find the critical value: The critical value is determined based on the desired level of confidence. For a 95% confidence interval, the critical value is approximately 1.96.
Use the formula: The formula to calculate the minimum sample size is given by n = (Z * σ / E)^2, where n is the sample size, Z is the critical value, σ is the population standard deviation (if known), and E is the margin of error.
In this case, since the population standard deviation is not provided, we can use a conservative estimate by assuming the worst-case scenario of σ = 0.5 (assuming a binary outcome, such as success or failure).
Substitute values and solve: Plugging in the values into the formula, we have n = (1.96 * 0.5 / 0.03)^2. Calculating this expression gives us the minimum sample size required to achieve a 95% confidence interval with a width no more than 6%.
Note that the formula used assumes a finite population size. If the population is very large or infinite, a different formula may be used (such as using a 1.96 critical value for large samples).
To learn more about margin of error click here:
brainly.com/question/29419047
#SPJ11
HI umm CAN YOU PLEASE ANSWER ASAP!!!!
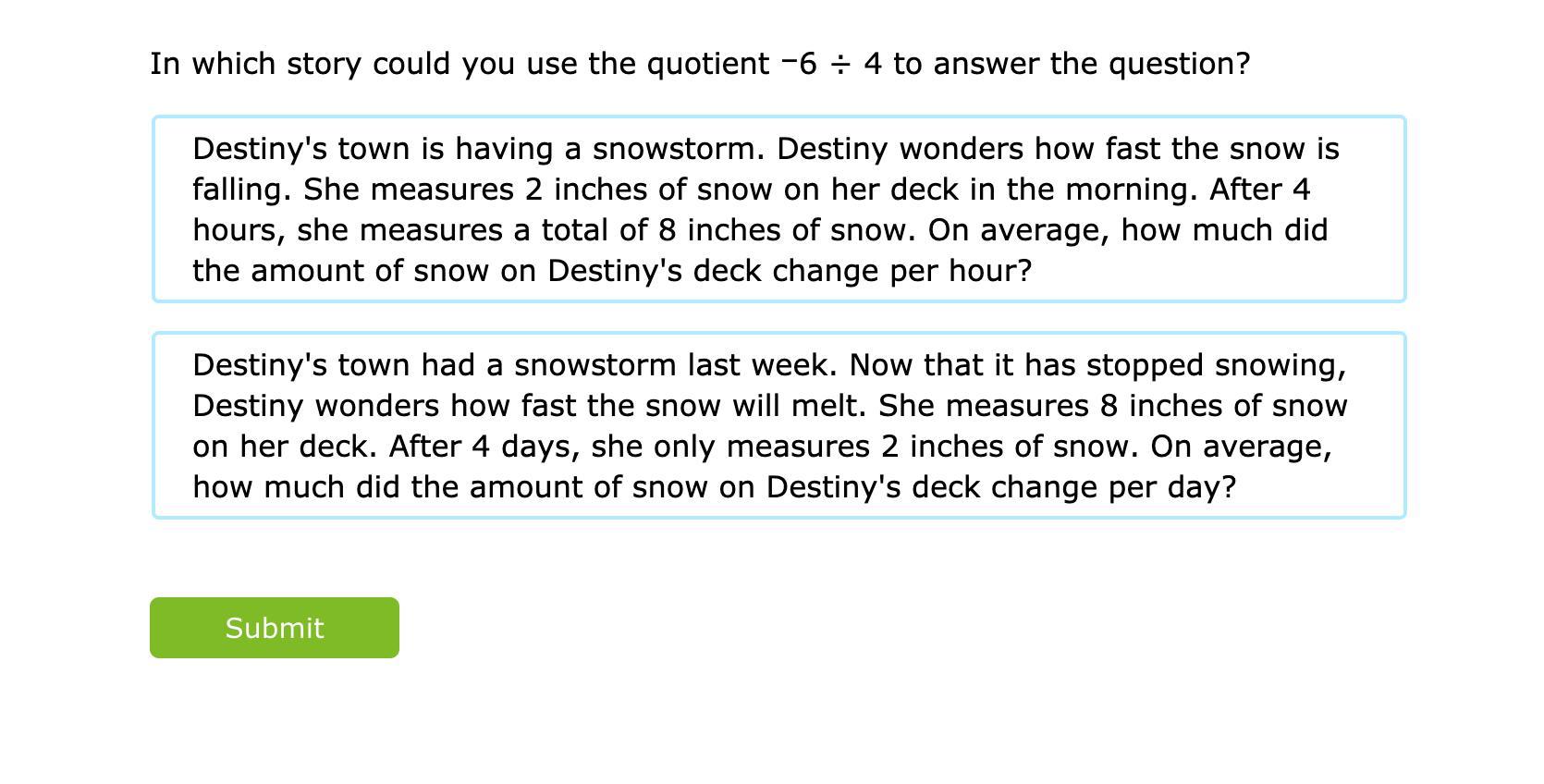
Answers
Answer:
2
Step-by-step explanation:
-6 divided by a positive number would make it a positive number welcome
How do you know if results are practically significant?
Answers
In order to determine the practical significance requires considering both the effect size measures and the context of the study
One way to determine practical significance is by using effect size measures. Effect size is a standardized measurement of the magnitude of a treatment or intervention.
A common equation used to calculate effect size is Cohen's d, which is the difference between the means of two groups divided by the standard deviation.
Another equation used is the odds ratio, which is the ratio of the odds of an event occurring in one group compared to another.
Additionally, it is important to consider the context of the study when evaluating practical significance.
To know more about ratio here
https://brainly.com/question/13419413
#SPJ4
PLS HELP ASAP I WILL GOVE 50 POINTS AND BRAINLEIST!!!!
A regular pentagon and a regular hexagon are both inscribed in the circle below, Which shape has a bigger area? explain your reasoning.

Answers
The shape that has a bigger area is the regular hexagon
Explaining the shape that has a bigger areaFrom the question, we have the following parameters that can be used in our computation:
Regular pentagonRegular hexagonBoth of these shapes are inscribed in a circle
By comparison, the number of sides are
Pentagon = 5 sides
Hexagon = 6 sides
This means that the regular hexagon has a larger area
The large area is as a result of the larger number of sides and longer side length compared to the regular pentagon.
Read more about area at
https://brainly.com/question/24487155
#SPJ1
The height of the sail on a boat is 7 feet less than 3 times the length of its base. If the The area of the sail is 68 square feet, find its height and the length of the base.
Answers
Step-by-step explanation:
It is given that,
The height of the sail on a boat is 7 feet less than 3 times the length of its base.
Let the length of the base is x.
ATQ,
Height = (3x-7)
Area of the sail is 68 square feet.
Formula for area is given by :
\(A=lb\\\\68=x(3x-7)\\\\3x^2-7x=68\\\\3x^2-7x-68=0\)
x = 8 feet and x = -3.73 feet
So, length is 8 feet
Height is 3(8)-7 = 17 feet.
So, its height and the length of the base is 17 feet and 8 feet respectively.
Please Help!!! Brainliest will be rewarded

Answers
The combined saving of Lucas and Owen is equal to $210.
What are ratios and proportions?An ordered pair of numbers a and b, represented as a / b, is a ratio if b is not equal to 0. A proportion is an equation that sets two ratios at the same value. The numerical relationship between two values demonstrates how frequently one value contains or is contained within another.
Given that the ratio of Owen's and Lucas's savings is 4:3. The ratio becomes 8:5 when 120 is added to Owen's and 60 is added to Lucas's amount.
The combined income will be calculated as,
O / L = 4 / 3
3O = 4L
6O = 8L
The new equation is,
( O + 120 ) / ( L + 60) = 8 / 5
8L - 5O = 120
Now solve the equation to get the values of O and L.
8L - 5O = 120
6O - 5O = 120
O = 120
The value of L will be,
L = ( 6O ) / 8
L = ( 6 x 120 ) / 8
L = 6 x 15
L = 90
Combine income = L + O
Combine income = 90 + 120 = $210
Therefore, the combined saving of Lucas and Owen is equal to $210.
To know more about ratios and proportions follow
https://brainly.com/question/2328454
#SPJ1
Write a recursive formula for the arithmetic sequence:
7,4,1,-2
Answers
a(sub)n = a(sub)n-1 - 3
(sub) indicates the values touching the parenthesis are written as a subscript.
The above would be the recursive formula as you are taking the previous number and subtracting 3 to get the next number in the sequence.
Answer:
N - 3
Step-by-step explanation:
It is a series of -3 so:
7 -3 = 4
4 - 3 = 1
1 - 3 = -2
So:
N-3
where N is the present value in the sequence.
how many license plates can be made using either 3 digits followed by 3 letters, or 3 letters followed by 3 digits?
Answers
Answer:
infinite
Step-by-step explanation:
the law in most states in the usa states there must be 3 letters and 3 numbers so there could be infinite
-hope this helps-
Farmer Jim keeps 12 hens in every cooper if farmer Jim has 20 coops how many hens does her in all if every hens lays 9 on Monday how many eggs will farmer Jim collect on Monday
Answers
Question
Farmer Jim keeps 12 hens in every cooper if farmer Jim has 20 coops
a) how many hens does she have ?
b) if every hens lays 9 eggs on Monday how many eggs will farmer Jim collect on Monday
Answer:
a) 240 hens
b) 2160 eggs
Step-by-step explanation:
a) Farmer Jim keeps 12 hens in every cooper if farmer Jim has 20 coops
Hence,
1 coop = 12 hens
20 coops = y hens
Cross Multiply
y hens = 20 coops × 12 hens/1 coop
y hens = 240 hens
Therefore Farmer Jim has 240 hens
b) We are told in question b that: if every hens lays 9 eggs on Monday how many eggs will farmer Jim collect on Monday?
From question a) we determine that the number of hens that Farmer Jim has:
240 hens
Hence,
1 hen = 9 eggs
240 hens = z eggs
z eggs = 240 hens × 9 eggs/1 hen
z eggs = 2160 eggs
Therefore, on Monday Farmer Jim will collect 2160 eggs
AB is the mid segment of the isosceles trapezoid WXYZ solve for the length of AB
Please helppppp

Answers
Answer:
8 units
Step-by-step explanation:
2(3x-3)=4x-1
6x-6=4x-1
2x=5
x=2.5
3x-3
3(2.5)-3
4.5
Please help it’s due in an hour

Answers
how to find the mean salary of 20 workers 12 men 8 women
Answers
To find the mean salary of 20 workers, 12 men and 8 women, you need to follow these steps:
Add the salaries of all 20 workers.Divide the total salary by the total number of workers (20) to find the average salary.Assuming you have the salaries of all 20 workers, the steps above will give you the mean salary. If you only have the salaries of the men and women separately, you can find the mean salary for each group and then take a weighted average based on the proportion of men and women in the sample. For example:
Add the salaries of the 12 men and divide by 12 to find the mean salary for men.Add the salaries of the 8 women and divide by 8 to find the mean salary for women.Multiply the mean salary for men by 12 and the mean salary for women by 8.Add the two products from step 3 and divide by 20 to find the weighted mean salary for all 20 workers.Learn more about mean at https://brainly.com/question/23045461
#SPJ11
The mean salary of all 20 workers is $46,000.
To find the mean salary of 20 workers, 12 men and 8 women, you need to sum up the total salaries of all the workers and divide by the total number of workers (20).
Assuming you have the salaries of all 20 workers, you can add up the salaries of all the workers and divide by 20 to get the mean salary.
If you don't have the salaries of each worker but have the average salary of men and women separately, you can use the weighted average formula to find the overall mean salary.
If the average salary of men is $50,000 and the average salary of women is $40,000, you can calculate the overall mean salary as follows:
(mean salary of men * number of men + mean salary of women * number of women) / total number of workers
= (50,000 * 12 + 40,000 * 8) / 20
= 46,000
Therefore, the mean salary of all 20 workers is $46,000.
Click the below link, to learn more about Mean:
https://brainly.com/question/31101410
#SPJ11
Your complete question is:
How to find the mean salary of 20 workers 12 men 8 women, If the average salary of men is $50,000 and the average salary of women is $40,000?
What percentage of the data values represented on a box plot falls between the lower quartile and the upper quartile?.
Answers
So, the percentage of data values represented on a box plot that falls between the lower quartile and the upper quartile is 50%.
In a box plot, the lower quartile (Q1) represents the 25th percentile, and the upper quartile (Q3) represents the 75th percentile. The interquartile range (IQR) is the range between the lower quartile and the upper quartile. To determine the percentage of data values that fall between the lower quartile and the upper quartile, we need to consider the IQR.
The IQR represents the middle 50% of the data. Therefore, the percentage of data values between the lower quartile and the upper quartile is 50%. In other words, half of the data values are within the IQR range, while the remaining 50% are outside this range, including the lower 25% below the lower quartile and the upper 25% above the upper quartile.
To know more about percentage,
https://brainly.com/question/14618268
#SPJ11
sec^2(pi/2 - x) [sin^2(x) – sin^4(x)]
Answers
it seems that is wrong.sorry for that.
![sec^2(pi/2 - x) [sin^2(x) sin^4(x)]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/MkpeMs6XnWEXUx5qUJqury4FbScQQkCI.jpeg)
i got b, but the answer is c.
can someone help please

Answers
64 out of 73 were opposed.
Set up a ratio as number opposed over number surveyed :
64/73 = x/657
Cross multiply:
73x = 42048
Divide both sides by 73:
X = 576
576 are opposed, now subtract this from total people surveyed:
657 - 575 = 81
81 are not opposed.
This is one that I have a lot of trouble with!

Answers
Given: The function given are
\(\begin{gathered} f(x)=4x^3+5x^2-3x-6 \\ g(x)=4x-5 \end{gathered}\)Required: To find the function-
\((f-g)(x)\)Explanation: The function can be determined as follows-
\((f-g)(x)=f(x)-g(x)\)Putting the values of the function f(x) and g(x)-
\(\begin{gathered} (f-g)(x)=(4x^3+5x^2-3x-6)-(4x-5) \\ =4x^3+5x^2-3x-6-4x+5 \\ =4x^3+5x^2-7x-1 \end{gathered}\)Final Answer: Option A is correct.
Name the algebraic property demonstrated in the example below: (1 point) x ⋅ y ⋅ z = y ⋅ x ⋅ z
Answers
Answer:
commutative property of multiplication
Step-by-step explanation:
You are wrapping a birthday gift that is packaged in a specially made pyramid-shaped box. The base of the box measures 10 inches by 10 inches and the slant height is 6 inches. How much paper do you need to wrap the box?
Answers
Answer:
2 1/4
Step-by-step explanation:
The amount of paper needed to wrap the considered box which has dimension of 10 by 10 by 6 inches is 440 sq. inches
What is the surface area of cuboid?Let the three dimensions(height, length, width) be x, y,z units respectively.
The surface area of the cuboid is given by
\(S = 2(a\times b + b\times c + c\times a)\)
A box is usually in shape of a cuboid.
For this case, its dimensions are 10 inches, 10 inches, and 6 inches.
The amount of wrapper we need is approx same as the area of its surface (assuming we're going to measure the paper needed in terms of its area).
Thus, we get:
Amount of the paper we need to wrap the considered box = surface area of that box = surface area of cuboid of dimension 10 inch by 10 inch by 6 inches = S (say), then:
\(S = 2(10\times 10+ 10\times 6 + 6\times 10)\\S = 440\)(in sq. inches)
Thus, the amount of paper needed to wrap the considered box which has dimension of 10 by 10 by 6 inches is 440 sq. inches
Learn more about surface area of cuboid here:
https://brainly.com/question/13522634
What is the initial value of the function

Answers
Answer:
initial value = 5
Step-by-step explanation:
the initial value is the value of y when x = 0.
this is the same as the y- intercept.
from the graph at (0, 5 )
that is when x = 0 the initial value is 5