Tina is saving to buy a notebook computer. She has two options. The first option is to put $300 awayinitially and save $30 every month. The second option is to put $100 away initially and save $50 everymonth. After how many months would Tina save the same amount using either option? How muchwould she save with either option?
Answers
The first step is to state the equations that describe the given situations.
The first one says that she can put $300 away and save $30 every month. This, written as an expression is:
\(30x+300\)Where x is the number of months.
For the second option she can put $100 away and save $50 every month. This, written as an expression is:
\(50x+100\)Now, to find how many months would Tina save the same amount of money using either options make both expressions equal and solve for x:
\(\begin{gathered} 30x+300=50x+100 \\ 30x-50x=100-300 \\ -20x=-200 \\ x=\frac{-200}{-20} \\ x=10 \end{gathered}\)After 10 months she would have the same amount using either options.
To find how miuch would she save, use one of the expressions, any of them, and replace x for 10, for example, let's use the first expression:
\(30(10)+300=600\)She will save $600 using either option.
Related Questions
What is the solution to the following system of equations?
a. (3,-2)
b. (-3,1)
c. (-2,3)
d. (1,-3)
Answers
Have a wonderful day!:)
HELP I NEED THE ANSWERS QUICK
Answers
Answer:
$244
Step-by-step explanation:
Plug in the numbers and solve from there
$=3(r)+12(p)+10(t)
3(10)+12(12)+10(7)
30+144+70
$=244
A development economist is studying income growth in a rural area of a developing country. The last census of the population of this area, several years earlier, showed that mean household annual income was 425 dollars, and the variance of household income was 2500 (dollarssquared). A current random sample of 100 households yields a sample mean income of $433.75. Assume that household annual incomes are approximately normally distributed, and that the population variance is known still to be 2500. Test the null hypothesis that population mean income has not increased ( H0 : "m"(greek letter) greater than equal to< 425 ) against the alternative hypothesis that it has increased ( HA :"m"(greek letter > 425 ), at a 1% level of significance.
What is the form of the rejection region?
a. Reject H0 if x < cv
b. Reject H0 if x > cv
c. Reject H0 if x < cv or if x > cv
d. Reject H0 if x = cv 3
What is the critical value?
a. 436.63
b. 433.75
c. 425
d. 437.88
What is the conclusion of the hypothesis test?
a. Accept H0
b. Reject H0 in favor of HA
Answers
Answer:
Reject H0 if x > cv
Step-by-step explanation:
The hypothesis :
H0 : μ ≤ 425
H1 : μ > 425
Standard deviation, s = √2500 = 50
Sample size, n = 100
xbar = 433.5
The test statistic, Z :
(xbar - μ) / s/√n
(433.5 - 425) / 50/10
Z = 8.5 / 5 = 1.7
The decision region ;
|Z| > Z0.01 ; Reject H0
From Z table ;critical value, Z0.01 = 2.33
1.7 < 2.33 ; We fail to reject then Null and conclude that thee is no significant evidence support the claim that population mean income has increased.
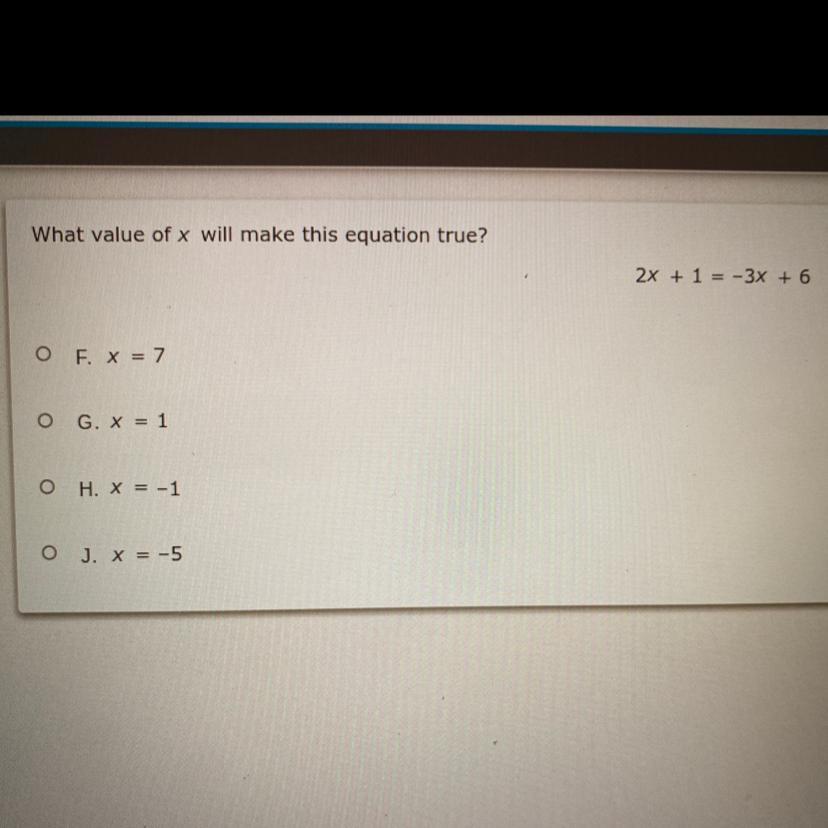
What are the answers to these questions?
Answers
Step-by-step explanation:
the inside expression of an absolute value expression can be positive or negative, but the result is only the positive one.
therefore, for our example here the negative case would be
2.5x - 6.8 = -12.9
which gives us
2.5x = -6.1
x = -6.1/2.5 = -2.44
and the positive case would be
2.5x - 6.8 = 12.9
and that gives us
2.5x = 19.7
x = 19.7/2.5 = 7.88
the squares of the first five whole numbers
Answers
Answer:
Square each number: 1 , 2 , 3 , 4 , 5:
1² = 1 * 1 = 1
2² = 2 * 2 = 4
3² = 3 * 3 = 9
4² = 4 * 4 = 16
5² = 5 * 5 = 25
~
Round 15,485,516 to the nearest ten thousands
Your answer
Answers
Answer:my answer is 15,490,000
Step-by-step explanation: cuz that is what rounding does
As the CAPS document outlines, the Content Specification and Content Clarification for Patterns, Functions, and Algebra shows sequenced mathematics content topics and a content area spread. In the Intermediate Phase, select one topic and report on the topic sequence and content area spread. Your report should demonstrate mathematics concepts and procedures’ hierarchical and logical progression.
Answers
Answer:
Step-by-step explanation:
In the Intermediate Phase of mathematics education, one topic that demonstrates a hierarchical and logical progression in patterns, functions, and algebra is the concept of "Linear Equations."
The topic of Linear Equations in the Intermediate Phase builds upon the foundation laid in earlier grades and serves as a stepping stone towards more advanced algebraic concepts. Here is an overview of the topic sequence and content area spread for Linear Equations:
Introduction to Variables and Expressions:
Students are introduced to the concept of variables and expressions, learning to represent unknown quantities using letters or symbols. They understand the difference between constants and variables and learn to evaluate expressions.
Solving One-Step Equations:
Students learn how to solve simple one-step equations involving addition, subtraction, multiplication, and division. They develop the skills to isolate the variable and find its value.
Solving Two-Step Equations:
Building upon the previous knowledge, students progress to solving two-step equations. They learn to perform multiple operations to isolate the variable and find its value.
Writing and Graphing Linear Equations:
Students explore the relationship between variables and learn to write linear equations in slope-intercept form (y = mx + b). They understand the meaning of slope and y-intercept and how they relate to the graph of a line.
Systems of Linear Equations:
Students are introduced to the concept of systems of linear equations, where multiple equations are solved simultaneously. They learn various methods such as substitution, elimination, and graphing to find the solution to the system.
Word Problems and Applications:
Students apply their understanding of linear equations to solve real-life word problems and situations. They learn to translate verbal descriptions into algebraic equations and solve them to find the unknown quantities.
The content area spread for Linear Equations includes concepts such as variables, expressions, equations, operations, graphing, slope, y-intercept, systems, and real-world applications. The progression from simple one-step equations to more complex systems of equations reflects a logical sequence that builds upon prior knowledge and skills.
By following this hierarchical progression, students develop a solid foundation in algebraic thinking and problem-solving skills. They learn to apply mathematical concepts and procedures in a systematic and logical manner, paving the way for further exploration of patterns, functions, and advanced algebraic topics in later phases of mathematics education.
Combine the likes terms to create an equivalent expression y - (-3y)
Answers
Answer:
4y
Step-by-step explanation:
y - (-3y)
y + 3y
4y
When you see two negatives they basically become an addition symbol. In this case you then add the like terms which are y and 3y to get 4y. Hope this helps!!
What is the GCF of 12, 30, and 18?
Answers
Answer:
6
Step-by-step explanation:
Answer: 6
The factors of 12 are: 1, 2, 3, 4, 6, 12
The factors of 18 are: 1, 2, 3, 6, 9, 18
The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30
Then the greatest common factor is 6.
Kay loves to save coins. She has a piggy bank that she has been filling for a long time with only dimes and nickels. Recently, her piggy bank was filled to the brim so Kay counted her coins and she discovered that she had $10. She also noticed that she has 11 less dimes than nickels. How many coins were in Kay's bank?
Answers
The total number of coins that were in Kay's bank are 137 coins.
How to determine the number of coins?In order to determine the number of dimes and nickels, we would assign a variables to the unknown numbers and then translate the word problem into algebraic equation as follows:
Let d represent the number of dimes.Let n represent number of nickels.Since she has 11 less dimes than nickels, an equation which models this situation is given by;
n = d + 11 ....equation 1.
Note: 1 nickel is equal to 0.05 dollar and 1 dime is equal to 0.1 dollar.
Additionally, the coins are worth 10 dollars;
0.1d + 0.05n = 10 ....equation 2.
By solving both equations simultaneously, we have:
0.1d + 0.05(d + 11) = 10
0.1d + 0.05d + 0.55 = 10
0.15d = 9.45
d = 63 dimes.
For nickels, we have:
n = d + 11
n = 63 + 11
n = 74
Now, we can determine the total number of coins;
Total number of coins = n + d
Total number of coins = 74 + 63
Total number of coins = 137 coins.
Read more on equations here: brainly.com/question/1511173
#SPJ1
How many ways can 5 different cards be dealt from a standard 52-card deck?
Answers
Answer:
There are 2598960 different ways to choose 5 cards from a standard 52-card deck.
Answer:
(52−5)5 = 2598960 different ways to choose 5 cards from the available 52 cards.
Step-by-step explanation:
Directions: Select the correct answer from each drop-down menu. Consider the expression below. 12x - 6x + 5 + 4x
If the expression is set equal to 10x + 5, then there would be solution(s).
If the expression is set equal to 10x + 7, then there would be solution(s).
If the expression is set equal to -10x + 5, then there would be solution(s).
Answers
Given statement solution is :- If the expression is set equal to 10x + 5, then there would be one solution.
If the expression is set equal to 10x + 7, then there would be no solution.
If the expression is set equal to -10x + 5, then there would be one solution.
If the expression 12x - 6x + 5 + 4x is set equal to 10x + 5, then there would be solution(s).
If the expression is set equal to 10x + 5, then there would be one solution.
If the expression is set equal to 10x + 7, then there would be no solution.
If the expression is set equal to -10x + 5, then there would be one solution.
For such more questions on Solutions to Given Equations
https://brainly.com/question/13729904
#SPJ8
What are the quartiles of the data
Answers
The quartiles of the data are: 60.5,64,66
Option(b) is correct.
The quartile divides the distribution into four groups and calculates the range of values above and below the mean.
A quartile separates the dataset into four categories by dividing the data into three points: the lowest, median, and upper quartiles.
Similar to how the median divides the data in half, with 50% of the measurements falling below it and 50% falling above it, the quartile divides the data into fourths, with 25% of the measurements falling below the lower quartile, 50% falling below the median, and 75% falling below the upper quartile.
The interquartile range, a measurement of variation around the median, is calculated using quartiles.
For the given data set: 58,60,60,61,62,64,64,64,66,70,72
Median = 64
Lower quartile = Median of the lower half = 60.5
Upper quartile = Median of the upper half = 66
Learn more about quartiles here:
https://brainly.com/question/10005803
#SPJ1
Can somebody please help?? i’ll give Brainliest to whoever answers first.
There are 625 students in Leon's school. He takes a random sample of 75 students from the entire school population. In the sample, 33
students are planning to attend the end of year picnic.
Based on his data, how many students from the entire school are planning to attend the end of year picnic? Show ALL your work!
Answers
Answer:
The answer is 275 students.
Step-by-step explanation:
In 75 students, 33 students attend.
So the ratio is 33/75.
so multiply with 625.
625 x 33/75 = 275
The Venn diagram below shows the events A and B, and the probabilities p, q and r.
It is known that P(A)=0.43 , P(B)=0.62 and P(A∩B)=0.27 .
Calculate the value of p
Calculate the value of q
Calculate the value of r
Find the value of P (A given NOT B)
Answers
The value of q is 0.35.
The value of p is 0.16.
The value of r is 0.27.
The value of P(A given NOT B) is approximately 0.4211.
To calculate the values of p, q, and r, we can use the information provided in the Venn diagram and the probabilities of events A and B.
Given:
P(A) = 0.43
P(B) = 0.62
P(A∩B) = 0.27
Calculating the value of p:
The value of p represents the probability of event A occurring without event B. In the Venn diagram, p corresponds to the region inside A but outside B.
We can calculate p by subtracting the probability of the intersection of A and B from the probability of A:
p = P(A) - P(A∩B)
= 0.43 - 0.27
= 0.16
Therefore, the value of p is 0.16.
Calculating the value of q:
The value of q represents the probability of event B occurring without event A. In the Venn diagram, q corresponds to the region inside B but outside A.
We can calculate q by subtracting the probability of the intersection of A and B from the probability of B:
q = P(B) - P(A∩B)
= 0.62 - 0.27
= 0.35
Therefore, the value of q is 0.35.
Calculating the value of r:
The value of r represents the probability of both event A and event B occurring. In the Venn diagram, r corresponds to the intersection of A and B.
We are given that P(A∩B) = 0.27, so the value of r is 0.27.
Therefore, the value of r is 0.27.
Finding the value of P(A given NOT B):
P(A given NOT B) represents the probability of event A occurring given that event B does not occur. In other words, it represents the probability of A happening when B is not happening.
To calculate this, we need to find the probability of A without B and divide it by the probability of NOT B.
P(A given NOT B) = P(A∩(NOT B)) / P(NOT B)
We can calculate the value of P(A given NOT B) using the provided probabilities:
P(A given NOT B) = P(A) - P(A∩B) / (1 - P(B))
= 0.43 - 0.27 / (1 - 0.62)
= 0.16 / 0.38
≈ 0.4211
Therefore, the value of P(A given NOT B) is approximately 0.4211.
for such more question on value
https://brainly.com/question/27746495
#SPJ8
Here are the shopping times (in minutes) of ten shoppers at a local grocery store.
Complete the grouped frequency distribution for the data.
In the distribution, the frequency of a class is the number of shopping times in that class.
(Note that we are using a class width of 5.)
Answers
The frequency which is to filled in the table is 1, 4, 2 and 4.
Given that;
All shopping time of ten shopkeeper:
25, 29, 25, 18, 24, 28, 36, 25, 33, 37
We have to complete the frequency in the table. Frequency of something is the number of times that number is coming.
Since, Shopping time is given as ,
25, 29, 25, 18, 24, 28, 36, 25, 33, 37
And, Intervals for which frequency is given is ,
18 to 22, 23 to 27, 28 to 32, 33 to 37.
Hence, WE get;
Numbers in the range 18 to 22 = 18 therefore 1
Numbers in the range 23 to 27 = 25, 25, 24, 25 therefore 4
Numbers in the range 28 to 32 = 29, 28 therefore 2
Numbers in the range 33 to 37 = 36, 33, 37, therefore 3
Hence, the frequency which is to filled are 1, 4, 2 and 4.
Learn more about frequency visit:
brainly.com/question/254161
#SPJ1
Keep getting stuck on this question don’t really understand what to do
Answers
The Solution:
Given the functions below:
\(\begin{gathered} f(x)=-4x-8 \\ \text{and} \\ g(x)=3x^2+x \end{gathered}\)We are required to find the value of f(-1)g(2)
So,
\(f(-1)\text{ means that we should substitute -1 for x in f(x)}\)\(f(-1)=-4(-1)-8=4-8=-4\)Similarly,
g(2) means we should substitute 2 for x in g(x).
\(g(2)=3(2)^2+2=3(4)+2=12+2=14\)Now, we shall multiply f(-1) and g(2) together.
\(f(-1)g(2)=f(-1)\times g(2)=-4\times14=-56\)Therefore, the correct answer is [option C]
Find the slope.
2
3) y=-x + 5
5
=
12
C)-
A
)
B)
5
2
D)
2
5
Answers
Answer:
D
Step-by-step explanation:
Snow-House sells a $1,501 snow thrower on the installment plan. The installment agreement includes a 20% down payment and 12 monthly payments of $170 each. What is the finance charge?
Answers
Answer:
$839.20
Step-by-step explanation:
To find the finance charge, we need to first calculate the total amount financed, which is the price of the snow thrower minus the down payment.
The down payment is 20% of $1,501, which is:
0.20 x $1,501 = $300.20
So the total amount financed is:
$1,501 - $300.20 = $1,200.80
The total amount of the 12 monthly payments is:
12 x $170 = $2,040
The finance charge is the difference between the total amount of the payments and the amount financed:
$2,040 - $1,200.80 = $839.20
Therefore, the finance charge is $839.20.
Judith has just become eligible to participate in her company’s retirement plan. Her company does not match contributions, but the plan does average an annual return of 12%. Judith is 40 and plans to work to age 65. If she contributes $200 per month, how much will she have in her retirement plan at retirement?
Answers
Answer:
She will have $375,769.33 in her retirement plan at the time of retirement.
Explanation:
The future value of an annuity is the value of a group of recurring payments at a certain date in the future, assuming a particular rate of return or discount rate.The higher the discount rate, the greater the annuity's future value.According to the question,
Periodic Payments(P) = $200
Rate of Return(r) = 12%(annual)
\(=\frac{12}{12}%\)
= 1% monthly
= 0.01
Number of payments(n) = 65 - 40
= 25(annual)
= 25 × 12 monthly
= 300 monthly
Future value =?
The formula for calculating future value is:
Future Value = \(P[\frac{(1+i)^{n}-1 }{i}]\)
= \(200[\frac{(1+0.01)^{300}-1 }{0.01}]\)
= \(200[\frac{19.7884663-1}{0.01}]\)
= 200[1878.84663]
= 375,769.326
= 375,769.33
Final Answer:
Therefore, the future value of her retirement when she retires is
$ 375,769.33 .
To learn more about the future value of the annuity, visit:
brainly.com/question/13119823
#SPJ9
For the following exercises, evaluate the functionf at the indicated values.
1. W (x, y) = 4x2 + y
2. Find W (2 - 1) , W (-3, 6) .
Answers
Answer:
\(W (2, -1) = 15\)
\(W (-3, 6) = -30\)
Step-by-step explanation:
Given
\(W (x, y) = 4x^2 + y\)
Required
Find W (2 - 1) , W (-3, 6) .
Solving (1): W (2, - 1)
Substitute 2 for x and -1 for y
\(W (x, y) = 4x^2 + y\)
\(W (2, -1) = 4 * 2^2 + (-1)\)
\(W (2, -1) = 16 -1\)
\(W (2, -1) = 15\)
Solving (2): W (-3, 6)
Substitute -3 for x and 6 for y
\(W (x, y) = 4x^2 + y\)
\(W (-3, 6) = 4 * (-3^2) + 6\)
\(W (-3, 6) = -36 + 6\)
\(W (-3, 6) = -30\)
Help help help help I really need help on this question please
Answers
Answer:60 cents per taco
Step-by-step explanation:
120/2=60
180/3=60
300/5=60
480/8=60
Solving by Completing the Square
Answers
Answer:
16
Step-by-step explanation:
Hello,
\(x^2-8x=10 \text{ *** we complete the square ***}\\ \\(x-4)^2-4^2=10 <=> (x-4)^2-16=10 \text{ *** we add 16 to both sides ***}\\\\(x-4)^2-16\boxed{+16}=(x-4)^2=10\boxed{+16}=26\)
Thanks
harriet is making loaves of bread for her grandmothers bakery. she has 12 1/2 cups of flour. the recipe calls for 5 1/2 cups of flour to make 3 loaves of bread. which equation can be used to find L, the total number of loaves of bread harriet can make
A 12 1/2 x 5 1/2 = L/3
B 12 1/2 divided by 5 1/2 = L/3
C 12 1/2 + L/3 = 5 1/2
D 12 1/2 - L/3 = 5 1/2
Answers
9514 1404 393
Answer:
B 12 1/2 divided by 5 1/2 = L/3
Step-by-step explanation:
The proportion ...
(recipe flour)/(recipe loaves) = (available flour)/(available loaves)
can be rearranged to ...
(available flour)/(recipe flour) = (available loaves)/(recipe loaves)
(12 1/2) / (5 1/2) = L / 3 . . . . . . matches choice B
Can someone please help me :(
Answers
Answer:
1
Step-by-step explanation:
2x + 1 = -3x + 6
add 3x
5x + 1 = 6
subtract 1
5x=5
Divide by 5
x=1
If this is correct, please mark brainliest!
Answer:
x=7
Step-by-step explanation:
2x + 1 = 15
-3x+6 = - 15
Since they are equal the equation is true
Solve the inequality.
Question 1
3y≤−9
The solution is
Answers
The solution of the given inequality is y ≤ -3.
The given inequality is -
3y ≤ −9
We have to solve this given inequality.
Now, we have the inequality as -
3y ≤ −9
=> y ≤ -3
Thus, the solution of the given inequality is y ≤ -3.
To learn more about inequality visit https://brainly.com/question/28823603
#SPJ1
If a middle school has 1,256 books to divide among 13 teachers. How many will each teacher get
Answers
Answer:
96.61
Step-by-step explanation:
Answer:
96 R (remainder) 8
Step-by-step explanation:
96 R8
1) In a class of 30 children, 18 of the children
are girls. What percentage of the class are
girls?
Name
Answers
Answer:
60%
Step-by-step explanation:
What percentage of 30 is 18?
Number or girls/Total number of students×100
= 18/30
= 0.6 × 100
= 60%
Point C has the same y-coordinate as point B and the distance between point B and point C is equal to the distance between point C and the y-axis. Point A has the same x-coordinate as point C and the distance between point A and point C is twice the distance between point B and point C. What is one possible location of point A? How many possible locations are there for point A?
Answers
The possible location of point A is (x, y), which is the same as the location of point B and point C, there is only one possible location for point A, and it is the same as the location of point B and point C.
Let's solve this step by step.
First, let's consider the information given:
Point C has the same y-coordinate as point B.
The distance between point B and point C is equal to the distance between point C and the y-axis.
Point A has the same x-coordinate as point C.
The distance between point A and point C is twice the distance between point B and point C.
Let's denote the coordinates of point B as (x, y), and we'll let y be the y-coordinate of point B.
From point 2, we know that the distance between point B and point C is equal to the distance between point C and the y-axis. This implies that point C lies on the vertical line passing through point B. So, the x-coordinate of point C is the same as that of point B, which is x.
From point 1, we know that point C has the same y-coordinate as point B, so the coordinates of point C are (x, y).
From point 4, we know that the distance between point A and point C is twice the distance between point B and point C. Since the distance between two points can be calculated using the distance formula, let's write the equations based on the given information:
Distance between point B and point C = Distance between point C and y-axis
√((x - x)² + (y - y)²) = √(x² + y²)
Simplifying the equation:
0 = √(x² + y²) - √(x² + y²)
This implies that the distance between point B and point C is 0, which means point B and point C coincide. Therefore, point A and point C also coincide since they have the same x-coordinate.
In summary, the possible location of point A is (x, y), which is the same as the location of point B and point C. So, there is only one possible location for point A, and it is the same as the location of point B and point C.
For such more questions on One Location for Point A
https://brainly.com/question/31857605
#SPJ8
1. The full Renegade dance Jalaiah created is 56 seconds long. For a 15-second-long TikTok, what percent of Renegade is used?
Answers
Answer:
3.7
Step-by-step explanation:
You have to divide
Answer:
i do not know tbh .
Step-by-step explanation: