Three boxes are stacked one on top of the other. One box is 3 feet 5 inches tall, one is 5 feet 11 inches tall, and one is 4 feet 9 inches tall. How high is the stack?
Write your answer in feet and inches. Use a number less than 12 for inches.
Answers
Answer:
14 ft. and 1 in. (14' 1")
Step-by-step explanation:
First, you add all of the feet together.
3 + 5 + 4 = 12 ft.
Next, add all of the inches.
5 + 11 + 9 = 25 in.
Because 12 inches is equal to 1 foot, we need to divide 12 into 25, which gives us 2 ft. and 1 in.
But that's not all. Lastly, you need to put everything together.
12 + 2 = 14 ft, and 1 in.
Hope this helps.
Related Questions
You are choosing between two health clubs club a offers membership for a fee of $13 plus a monthly fee of $28 club B offers membership for a fee of $19 plus a monthly fee of $27 after how many months will the total cost of each health club be the same? What will be the total cost for each club?
Answers
To determine when the total cost of each health club will be the same, we can set up an equation and solve for the number of months.
Let's assume the number of months is represented by 'x'.
For Club A, the total cost is given by:
Total cost of Club A = $13 (one-time fee) + $28x (monthly fee)
For Club B, the total cost is given by:
Total cost of Club B = $19 (one-time fee) + $27x (monthly fee)
To find the number of months when the total cost is the same, we set the two equations equal to each other:
$13 + $28x = $19 + $27x
Simplifying the equation, we get:
$28x - $27x = $19 - $13
$x = 6
Therefore, after 6 months, the total cost of each health club will be the same.
To find the total cost for each club after 6 months, we substitute the value of 'x' back into the equations:
Total cost of Club A after 6 months = $13 + $28(6) = $13 + $168 = $181
Total cost of Club B after 6 months = $19 + $27(6) = $19 + $162 = $181
So, the total cost for both Club A and Club B will be $181 after 6 months.
For such more question on equation
https://brainly.com/question/29174899
#SPJ8
Find the length of AC. Round your answer to two decimal places. A 10 in. b 40° C B a

Answers
Using relations in a right triangle, it is found that the length of AC is of 6.43 inches.
What are the relations in a right triangle?The relations in a right triangle are given as follows:
The sine of an angle is given by the length of the opposite side to the angle divided by the length of the hypotenuse.The cosine of an angle is given by the length of the adjacent side to the angle divided by the length of the hypotenuse.The tangent of an angle is given by the length of the opposite side to the angle divided by the length of the adjacent side to the angle.In this problem, the length of side AC is b, which is opposite to the angle of 40º, while the hypotenuse is of 10 in, hence:
\(\sin{40^\circ} = \frac{b}{10}\)
\(b = 10 \times \sin{40^\circ}\)
Using a calculator:
\(b = 6.43\)
More can be learned about relations in a right triangle at https://brainly.com/question/26396675
10 point if you solve this

Answers
A downhill skier was able to move 560 meters in 25 seconds. What is the skier’s average speed? (Round your answer to the nearest tenth of a meter per second.)
Answers
Answer:
20 m/s
Step-by-step explanation:
560 m/25 s
=22.4 m/s
≈ 20 m/s ( nearest tenth of m/s )
Answer:
22.4
Step-by-step explanation:
Just divide 560 by 25 .
Prove that "If α is an ordinal and β ∈ α, then β is an ordinal" ?
Answers
If α is an ordinal and β ∈ α, then β satisfies all three properties of an ordinal. Therefore, β is also an ordinal.
To prove the statement "If α is an ordinal and β ∈ α, then β is an ordinal," we need to demonstrate that if α is an ordinal and β is an element of α, then β satisfies the three properties of an ordinal:
Well-Ordering: Every element of β is strictly well-ordered by the membership relation ∈. This property holds because α is an ordinal and satisfies the well-ordering property, and β being an element of α inherits this property.
Transitivity: For any two elements γ and δ in β, if γ ∈ δ and δ ∈ β, then γ ∈ β. Since β is an element of α and α is transitive, the transitivity property carries over to β.
Trichotomy: For any two elements γ and δ in β, either γ ∈ δ, δ ∈ γ, or γ = δ. Again, this property is inherited from α, as β is an element of α.
For more such questions on ordinal
https://brainly.com/question/30648205
#SPJ8
The figure shown a circle and two semicircles. O is the centre of the big circle.
The diameter of the big circle RQ is 56 cm. What is the area of the unshaded part? (Take
π: 22/7

Answers
The area of the unshaded part is 2464 cm²
How to solve for the areaThe diameter of 56 cm, which means the radius is half of that: 56/2 = 28 cm.
The area of a circle is given by the formula: A = πr², where r is the radius.
= π(28)²
= π(784)
= 2464 cm².
The two semicircles form a complete circle with a diameter of 56 cm, so each semicircle has a radius of 28 cm.
The area of a semicircle is half the area of a full circle.
So, the combined area of the two semicircles is:
A₂ = 0.5π(28)²
= 0.5π(784)
= 1232 cm².
The total area of the entire figure is:
total = A₁ + A₂
= 2464 cm² + 1232 cm² = 3696 cm².
Area of the shaded regions:
The shaded regions are the two semicircles, which have a combined area of A₂
= 1232 cm².
unshaded = A total - A₂
= 3696 cm² - 1232 cm²
= 2464 cm²
Read more on diameter here
https://brainly.com/question/23220731
#SPJ1
A group of 5 students was asked, "How many hours did you watch television last week?" Here are their responses:
14, 6, 18, 15, 13
Find the median and mean number of hours for these students.
If necessary, round your answers to the nearest tenth.
Median: hours
?
Mean: [hours

Answers
Find the solution to the situation “the number n divided by the number 5 equals 10”. Enter your answer in the box.
a 0.5
b 50
c 500
d 2
Answers
Answer:
B. 50
Step-by-step explanation:
n/5=10
n/5×5=10×5
n=50
what two numbers multiply to -120 and add to 37?
Answers
40 x -3= -120
40+-3= 37
If a car travels 200km in 2.5 hours, how far would it travel in 6 hours at the same rate of speed?
Answers
Answer: 480
Step-by-step explanation:
To solve this, you need to set up a proportion: 200/2.5 x/6
The 200 represents the km, and the 2.5 and 6 represent the hours. You can either solve this by multiplying 200 by 6 and setting it equal to 2.5 by x then solving for x, or you can find the rate the car travels in km in one hour. To do that, you divide 200 by 2.5 and get 80: this is your km per hour. Then you multiply that to 6 to see how far the car will go in 6 miles if it continues at the speed of 80 km per hour.
Answer:
Answer: 480 km
Step-by-step explanation:
As we know that if we keep speed or velocity constant, distance is directly proportional to time.
• In the first case:
\({ \rm{d_{1} = kt _{1}}}\)
d1 is 200 kmt1 is 2.5 hoursk is a constant of proportianality• Substitute the variables with their respective values to find the value of constant, k
\({ \rm{200 = (k \times 2.5)}} \\ \\ { \rm{k = \frac{200}{2.5} }} \\ \\ { \underline{ \rm{ \: \: k = 80 \: km {h}^{ - 1} \: \: }}}\)
• In the second case
\({ \rm{d _{2} = kt _{2} }}\)
d2 is what we needt2 is 6 hoursk is 80 kmh-¹\({ \rm{d _{2} = (80 \times 6)}} \\ \\ { \boxed{ \boxed{ \rm{ \: \: d _{2} = 480 \: km \: \: }}}}\)
Simplify: (8c2−10c−5)−(−9c2−9c−8).
Answers
= -c2-c+3
The length of a rectangle is 5 ft longer than its width.
If the perimeter of the rectangle is 46 ft, find its area.
Answers
A $35 item is marked as 25% off. What is the discounted price?
Answers
Answer:
$26.25
Step-by-step explanation:
35×.25=8.75
35-8.75= 26.25
plz give me brainliest
How many solutions does the system have?
You can use the interactive graph below to find the answer.
y = 3x + 3
y = -2x + 3
Choose 1 answer:
Exactly one solution
B
No solutions
Infinitely many solutions
Answers
solve;
i) X+10%of X =22
ii)x+20%of X=rs60
iii)X+25%ofx=rs120
iv)X=rs200+50%of X
v)X=180+10%of x
question from equation and inequality
Answers
Answer:
i) 20
ii) 50
iii) 96
iv) 400
v) 200
Step-by-step explanation:
Given equations, for which we have to solve for the variable.
i)
\(X+$10\% of X $=22\\\Rightarrow X + \dfrac{10}{100}X =22\\\Rightarrow \dfrac{11}{10}X=22\\\Rightarrow X = 20\)
ii)
\(x+$20\% of x = Rs.\ 60 $\\\Rightarrow x+\dfrac{20}{100}x =60\\\Rightarrow \dfrac{6}{5}x = 60\\\Rightarrow x = 50\)
iii)
\(x+$25\% of x = Rs. 120$\\\Rightarrow x + \dfrac{25}{100}x = 120\\\Rightarrow \dfrac{5}{4}x = 120\\\Rightarrow x = 96\)
iv)
\(X= $ Rs. 200+50\% of X$\\\Rightarrow \dfrac{50}{100}X = 200\\\Rightarrow X = 400\)
v)
\(X=180+$10\% of X$\\\Rightarrow X - \dfrac{10}{100}X = 180\\\Rightarrow \dfrac{9}{10}X = 180\\\Rightarrow X = 200\)
What is 2 ^ 4 in standard form?
Answers
use the table to write a proportion.

Answers
Answer:
22
Step-by-step explanation:
The weights of bags of chips are normally distributed with a mean of 180 grams and a standard deviation of 4 grams.
What percent of the bags of chips weigh less than 176 grams?
2.5%
16%
32%
34%
Answers
The percent of the bags of chips weigh less than 176 grams is b 16%
What percent of the bags of chips weigh less than 176 grams?From the question, we have the following parameters that can be used in our computation:
Mean = 180
Standard deviation = 4
Bags of chips weigh less than 176 grams
This means that
x = 176
So, the z-score is
z = (176 - 180)/4
Evaluate
z = -1
The percent of the bags of chips weigh less than 176 grams is represented as
P = P(z < -1)
Using a graphing calculator, we have
Percentage = 0.15866
So, we have
Percentage = 16%
Hence , the percentage is 16%
Read mroe about z-scores at
brainly.com/question/25638875
#SPJ1
This year, a small business had a total revenue of 28900 . If this is 15% less than their total revenue the previous year, what was their total revenue the previous year?
Answers
The previous year's total revenue for the small business was approximately $25,130.43.
The total revenue of the small business the previous year can be calculated by finding the value that is 15% more than the revenue of $28,900 this year.
To determine the previous year's revenue, we can set up the equation:
Previous Year's Revenue + 15% of Previous Year's Revenue = $28,900
Let's solve the equation to find the previous year's revenue:
Let x be the previous year's revenue.
x + 0.15x = $28,900
Combining like terms, we have:
1.15x = $28,900
Dividing both sides by 1.15, we get:
x = $28,900 / 1.15 ≈ $25,130.43
Therefore, the previous year's total revenue for the small business was approximately $25,130.43.
We set up the equation by adding 15% of the previous year's revenue to the previous year's revenue. This is done to find the total revenue that is 15% more than the previous year's revenue. By solving the equation, we find that the previous year's revenue was approximately $25,130.43.
For more such answers on revenue
https://brainly.com/question/30495119
#SPJ8
Raspberries cost twice as much as blueberries. The prices of blueberries and raspberries represent proportional relationships. Select all of the graphs that could represent the cost of raspberries and blueberries.
Answers
Graph 1 and 3 will represent the cost of raspberries and blueberries perfectly.
How to illustrate the graph?The general equation of a straight line is
[y] = [m]x + [c]
where -
[m] → is slope of line which tells the unit rate of change of [y] with respect to [x].
[c] → is the y - intercept i.e. the point where the graph cuts the [y] axis.
The equation of straight line also represents direct proportionality as y = mx
m = y/x
[m] is constant of proportionality.
We have Raspberries (R) cost twice as much as blueberries (B). The prices of blueberries and raspberries represent proportional relationships. In this case, 1 and 2 Illustrates this perfectly.
Learn more about graph on:
https://brainly.com/question/19040584
#SPJ1
Complete question
Raspberries cost twice as much as blueberries. A B The prices of blueberries and raspberries represent proportional relationships. Cost (dollars) Raspberries Weight (lb.) Raspberries Select all of the graphs that could represent the cost of raspberries and blueberries. (Select all that apply.)

(1) y - 11 = 4
(2) y = 2x + 3
Answers
Answer:
y = 15 , x = 6
Step-by-step explanation:
you can easily find y from first equation
Move y to the other side of the equation and reverse its sign
so (-11) changes to (+11) and now we have this equation
y = 15
now you must replace 15 instead of y in second equation ,then we have this equation
15 = 2x + 3
now we have to find x
move (+3) to other side of equation and reverse its sign
(+3) changes to (-3)
we have this equation now
15 - 3 = 2x
12 = 2x
x = 12 ÷ 2 = 6
A baseball team plays in a stadium that holds 52000 spectators. With the ticket price at $9 the average attendance has been 21000. When the price dropped to $7, the average attendance rose to 26000.a) Find the demand function p(x) where x is the number of the spectators. (Assume that p(x) is linear.) p(x)=----------------b) How should ticket prices be set to maximize revenue? The revenue is maximized by charging $ --------per ticket.
Answers
The required demand function and revenue per ticket are p(x) = -0.4 * (x - 21000) + $9 and $9.
How to find demand function?a) To find the demand function p(x), we can use the two data points: (21000, $9) and (26000, $7). To find the slope of the demand function, we can use the formula:
slope = (change in price) / (change in attendance)
Plugging in the two data points, we get:
slope = ($9 - $7) / (26000 - 21000) = -$2 / 5000 = -0.4
To find the y-intercept, we can use either data point and the slope we just found. Let's use the first data point:
p(x) = slope * (x - 21000) + $9
Now we have our demand function:
p(x) = -0.4 * (x - 21000) + $9
b) To maximize revenue, we need to find the price that will result in the maximum number of tickets sold. This is equal to the price that corresponds to the peak of the demand function, or the maximum value of x for which p(x) is decreasing. To find this, we can take the derivative of the demand function and set it equal to zero:
dp/dx = -0.4 = 0
x = 21000
So the maximum revenue is obtained by selling 21000 tickets at the price of $9 each, for a total revenue of $189,000. To maximize revenue, the ticket price should be set at $9.
To know more about function visit:
brainly.com/question/28278699
#SPJ4
William leaves his home at 15:03 and walks for 12 minutes to Euston station.
He spends 4 minutes buying a ticket and then catches the next train to Bletchley.
What time will he arrive at Bletchley?
Train timetable
Euston
14:49 15:18 15:29
14:52
15:32 15:35
Harrow
Watford 15:01
15:30
15:41 15:44 16:11
Hemel
15:39 15:50
15:53
16:20
Tring
15:31
16:00
Q
16:14 16:41
Bletchley 15:47
16:16
16:30
Bedford 15:54 16:23 16:34 16:37 17:04
15:32 15:59
Answers
To find out what time he will arrive at Bletchley, we need to look at the arrival time for the train that departs Euston at 15:32. According to the timetable, this train arrives at Bletchley at 16:16.
William spends 12 minutes walking to Euston station and 4 minutes buying a ticket, so his total journey time is 12 + 4 + 44 = 60 minutes (since there are 60 minutes in an hour). Therefore, he will arrive at Bletchley at 16:16 + 60 minutes = 17:16.
So, William will arrive at Bletchley at 17:16.
*Answer*
15:47
Step-by-step explanation:
He left; 15:03
Walk for; 12mins
Spends extra;4min
So by my side,
I'll sum up those values we're having to find the total time that was spent
12+4= 16mins
So, at that time when he reached at the station it was 15:19 when we add those extra mins
And so I think it'll 15:47
My thought told me so though
of the following fractions which is 50% greater than 3/7
Answers
Answer:
9/14
Step-by-step explanation:
3/7 + 50%×3/7 =
= 3/7 + 1/2×3/7
= 3/7 + 3/14
= 6/14 + 3/14
= 9/14
The required fraction which 50% grater than 3/7 is 9/14.
Fraction to determine that 50% grater than 3/7.
Fraction of the values is number represent in form of Numerator and denominator.
Here, fraction = 50% grater than 3/7
= 1.5 x 3/7
= 4.5/7
= 45/70
= 9/14
Thus, The required fraction which 50% grater than 3/7 is 9/14.
Learn more about fraction here:
https://brainly.com/question/10354322
#SPJ5
what is the value of the expression shown below
2 3/5 - 1 3/5
^ ^
TWO THREE-FIFTHS MINUS ONE THREE-FIFTHS
THE NUMBERS ARE MIXED FRACTIONS
Answers
Answer:
1
Step-by-step explanation:
1. One way to do this is converting both into improper fractions. To do this, multiply the whole number by the denominator and add that to the numerator.
2 3/5 --> 2*5 is 10 --> 10+3 is 13. --> 13/5
2. This leaves us with 13/5 - 8/5
3. Subtract the numerators
13/5 - 8/5 = 5/5
4. Simplify. If the numerator is the same number as the denominator, it's a whole number.
5/5 = 1
2.
(05.02)
A triangle can be formed with side lengths 2 in, 3 in, and 6 in. (5 points)
True
False
Answers
False
Explanation:
No, a triangle cannot be constructed with sides of 2 in., 3 in., and 6 in.
For three line segments to be able to form any triangle you must be able to take any two sides, add their length and this sum be greater than the remaining side.
Answer:
It's false! because 2 3 and 6 do not sum up to each side!
Step-by-step explanation:
x/6−7=12 what is x
if its a good enough answer I WILL GIVE BRAINLIEST
Answers
Answer:
x/6=12+7
x/6=19
x=19*6
x=114
Help!! I’m not sure what to do

Answers
Answer:
h=23
Step-by-step explanation:
triangle equals 180 degrees
180-40=140
140/4=35
Fill in the missing values below one at a time to find the quotient when
3x³ 10x + 4 is divided by a + 2.
30
+2
3.2.3
try

Answers
Answer:
Step-by-step explanation:
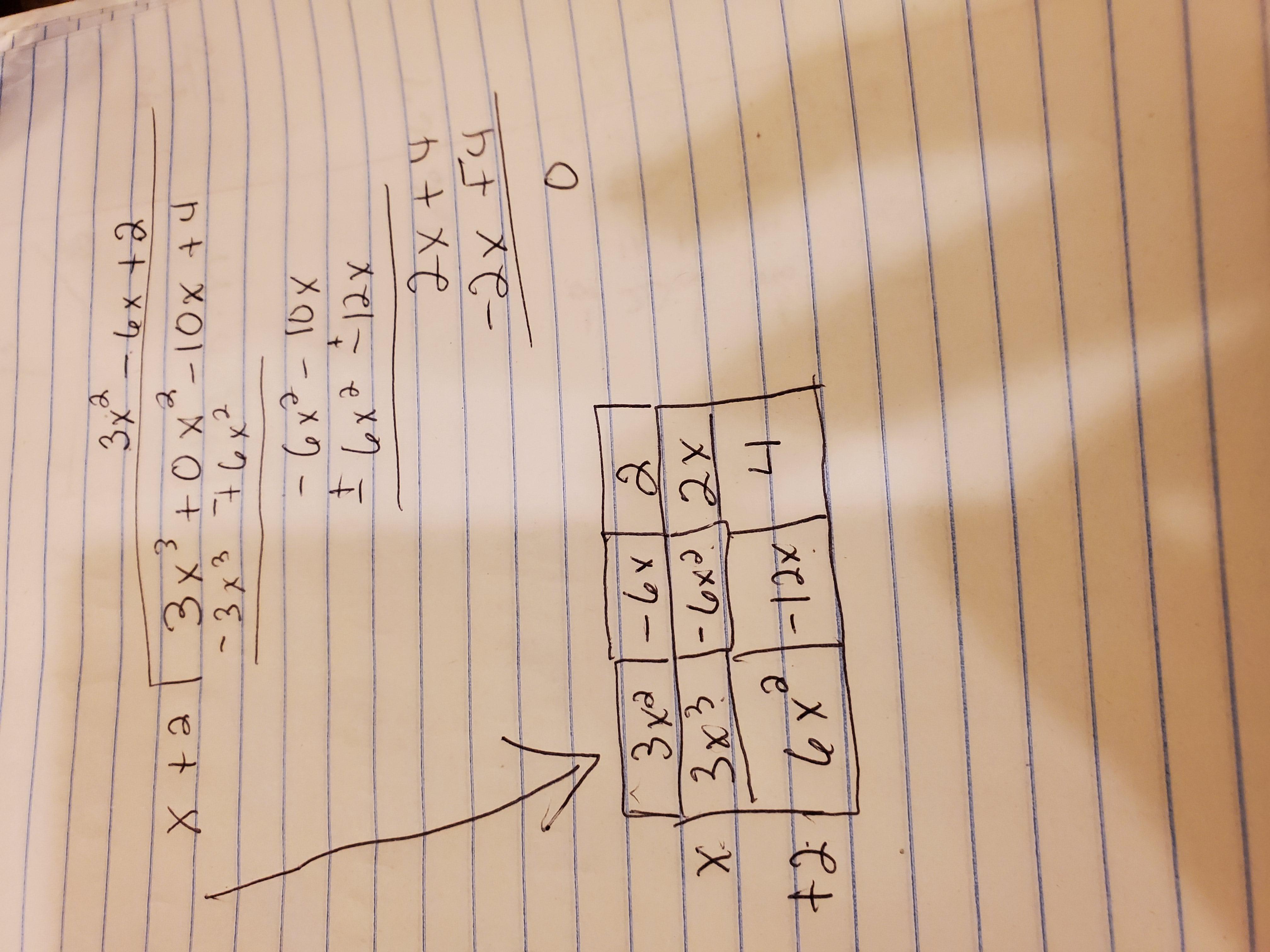
5x/8x^2+5x
Find the restricted values of x for the following rational expression. If there are no restricted values of x, indicate "No Restrictions".
Answers
Answer:
\(x\neq 0\)
Step-by-step explanation:
Dividing by 0 is undefined, hence not allowed.
The denominator of the first term contains x^2.
Hence 0 is not allowed.