**THIS IS DUE SOON, PLEASE HELP**Lin missed math class on the day they worked on expanding and factoring, Kiran is helping Lincatch upLin understands that expanding is using the distributive property, but she doesn'tunderstand what tactoring is or why it works. How can Kiran explain factoring to Lin?Lin asks Kiran to help her factor the expression -4xy - 12xz + 20xw. How can Kiran usethis example to Lin understand factoring?
Answers
You have to explain that factoring means to convert a combination of additions and/or subtractions of algebraic terms into a PRODUCT.
Under such premises, the use of the distributive property *in REVERSE form) is critical.
You should make clear that the first step consists in finding the COMMON factors for all terms. That is, the IDENTICAL factors that appear in ALL terms of the algebraic expression.
Then, given : - 4 x y - 12 x z + 20 x w
We start by writing all the numbers in each term as an expression of product of PRIME numbers:
- 4 = -1 * 2 * 2
- 12 = -1 * 2 * 2 * 3
20 = 2 * 2 * 5
then we look into what factors are common to all these three numbers. The answer is: 2 * 2 (4) is found common in all prime factor forms. Therefore, the factor "4" is going to be part of the factor we will be extracting.
Now the letter factors:
x y = x * y
x z = x * z
x w = x * w
So, the COMMON factor to all three letter expressions is "x".
Then we are going to extract "4 x" (4 times x) as factor common to all. This is similar to "divide"each term by "4 x".
then we do:
- 4 x y - 12 x z + 20 x w = 4 x ( - y - 3 z + 5 w)
The common extracted factor appears in bold outside the parenthesis, and we are lft inside the parqnthesis with the factors that were NOT common.
The explanation should continue with the "checking" of the correctness of the procedure performed. This is done by using now the Distributive Property aga\gain but to get rid of the parenthesis, and multiplying each term inside by the factor "4x" that we extracted, thus confirming that we get to the starting expression.
Related Questions
What the meaning of statement this?

Answers
The statement is asserting that the universal class (V) is defined as the collection of all sets, where every set is included. It signifies that V encompasses all possible sets within the given set theory framework.
The statement "The universal class set, or universe, is the class of all sets: V = {x: x = x}" is referring to the concept of the universal class or the universe in set theory.
In set theory, the universal class set, denoted as V, represents the collection or class that contains all sets. It includes every possible set that can be defined or exists within the context of the set theory being considered.
The notation "{x: x = x}" is used to define the elements of the universal class. Here, "x = x" represents a condition that is always true for any object or element, regardless of its nature. In other words, this condition holds for everything in the universe, as anything is equal to itself.
Learn more about sets here:
https://brainly.com/question/30705181
#SPJ1
y=2/3x-4 i need help i do not get this does anybody know slopes
Answers
Step-by-step explanation:
slope in this case is 2/3
this equation is in slope intercept form
y=mx+b
m is slope
and b is y-intercept
so
m =2/3
b=-4
Answer: The slope is 2/3 (0.666...)
Step-by-step explanation: The slope is the coefficient of X in slope-intercept form. y=2/3x-4 is in slope-intercept form (y=mx+b) m = slope, b = y-intercept (the Y value when the X is equal to 0)
On a graph, it looks like this:

\(9 + 3 (10 ÷ 2) - 5^2\)
Answers
\(9+3(10 \div 2)-5^2\\\\=9+3(5)-25\\\\=-16+15\\\\=-1\)
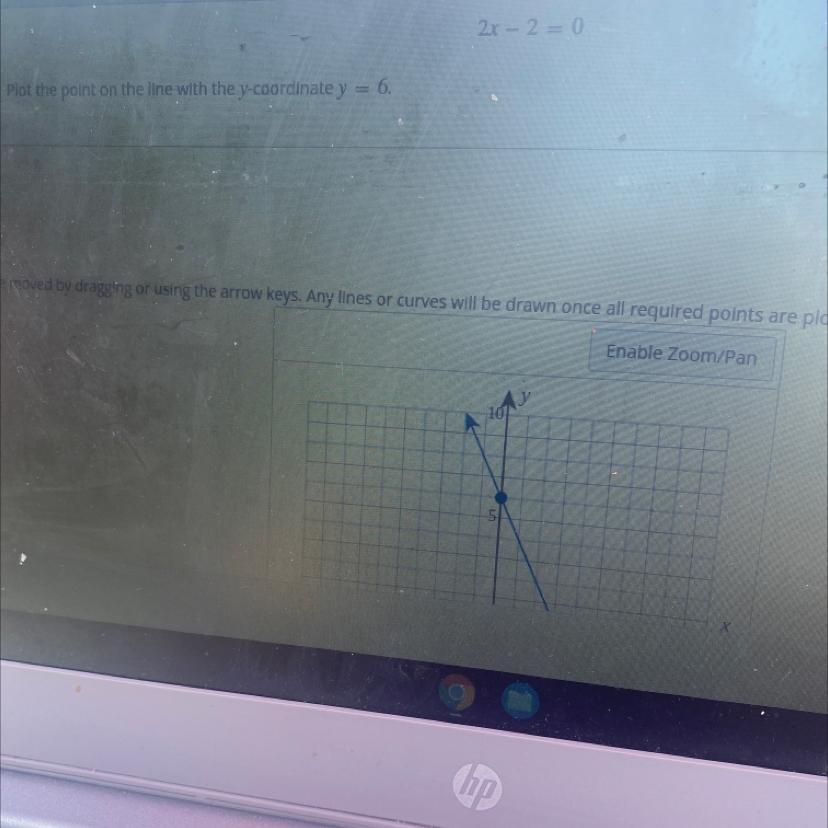
Plot the point on the line with the y- and y =6
Answers
In order to determine the point which coincides with y-coordinate y = 6, it is necessary to look for y = 6 on the y axis and then move to the right until the line is reached.
Based on the previous consideration, you get:
As you can notice, the point is (-1/2 , 6)
A rectangular prism has a length of 3 1/2 feet, a width of 5 1/3 feet, and a height of 12 feet. What is the volume of the prism?
Answers
Volume = length x width x height
First, we need to convert the mixed numbers to improper fractions:
3 1/2 = 7/2
5 1/3 = 16/3
Now we can substitute the values into the formula:
Volume = (7/2) feet x (16/3) feet x 12 feet
Multiplying the fractions and the whole number:
Volume = (7/2) x (16/3) x 12
Simplifying the fractions:
Volume = 56 cubic feet
Therefore, the volume of the rectangular prism is 56 cubic feet.
Answer:
The answer is 1054ft³
Step-by-step explanation:
Volume of rectangular prism =1/3LWH
V=1/3×31/2×51/3×12
V=1054ft³
12 dozen pieces of gum to a box 12 full boxes 1 ooen bix with 32 how many pieces of gum n all
Answers
The number of gums available, with the 12 boxes, each containing 12 dozens of gums and one open box containing 32 gums, found using the values of the non verbal units of measure, indicates that the number of gums are 1760 gums.
What is a non verbal unit of measure?Non verbal units of measure are used to describe the quantity of an item using verbal terms such as pairs (2 units), dozens (12 units), scores (20 units), gross (12 dozens or 144 units), bushels (8 gallons or 4 pecks), ream (500 units).
The number of dozens of pieces of gum are in a box = 12 dozens
The number of boxes of gum available = 12 boxes
The remaining number of gums = 1 open box with 32 gums
1 dozen of an items = 12 units of the specified item
12 dozens of an item = 1 gross of the item
The number of pieces of gums in a box, therefore is 1 gross of gums.
Therefore, the number of pieces of gum in all = 12 × 12 × 12 + 32 = 1760
The number of gums available are 1760 gumsLearn more about non numerical units of measure here:
https://brainly.com/question/7744911
#SPJ1
Express 602.16 dam in decimeters
Answers
The expression of 602.16 dam in decimeters can be written as 60216 decimeter.
How can the expression of 602.16 dam be converted to decimeters?The concept that will be used in the calculation is conversion. to perform this conversion, it is important to note that 1 Decimeter (dm) is equal to 0.01 dekameter (dam).
Then, if 1dm = 0.01 dam
Xdm = 602.16 dam
Where x is the value in decimeter.
Then we can cross multiply as :
X= (602.16 dam * 1dm)/ 0.01 dam
= 60216 decimeter.
Learn more about conversion at:
https://brainly.com/question/97386
#SPJ1
Please help me this is hard

Answers
Shaded Area=11*14 -5*7= 154- 35=119 sqm
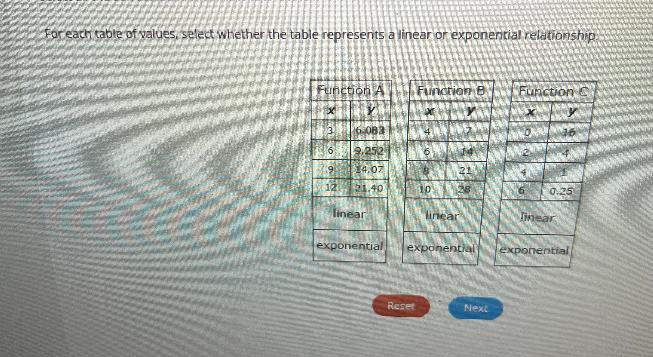
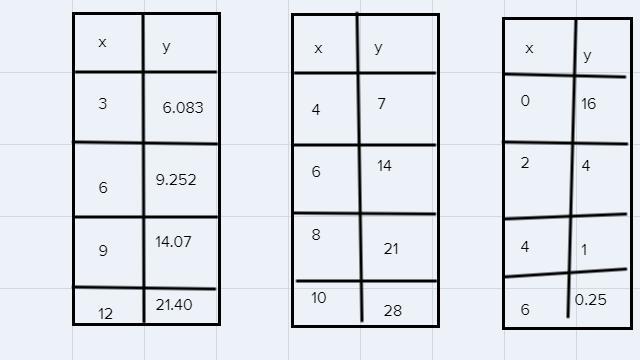
3Select all the correct locations below each table.For each table of values, select whether the table represents a linear or exponential relationship.Function Ay6.083X39.25214.0712 21.4069linearexponentialFunction Bу7X46810142128ResetlinearexponentialNextFunction CX y1602106410.25linearexponentially
Answers
Given:
The functions are:
Find-:
The function linear or exponential
Explanation-:
For linear function
\(m=\frac{y_2-y_1}{x_2-x_1}\)Check for points:
\(\begin{gathered} (x,y)=(3,6.083) \\ \\ (x,y)=(6,9.252) \\ \\ (x,y)=(9,14.07) \end{gathered}\)\(\begin{gathered} m=\frac{9.252-6.083}{6-3} \\ \\ m=1.056 \end{gathered}\)\(\begin{gathered} m=\frac{14.07-9.252}{9-6} \\ \\ m=1.606 \end{gathered}\)So, it is not a linear function it is an exponential function.
Function B
\(\begin{gathered} (x,y)=(4,7) \\ \\ (x,y)=(6,14) \\ \\ (x,y)=(8,21) \end{gathered}\)Then the slope is:
\(\begin{gathered} m=\frac{14-7}{6-4} \\ \\ m=\frac{7}{3} \end{gathered}\)\(\begin{gathered} m=\frac{21-14}{8-6} \\ \\ m=\frac{7}{2} \end{gathered}\)So, it is a linear function.
Function C-
\(\begin{gathered} (x,y)=(0,16) \\ \\ (x,y)=(2,4) \\ \\ (x,y)=(4,1) \end{gathered}\)\(\begin{gathered} m=\frac{4-16}{2-0} \\ \\ m=-6 \end{gathered}\)\(\begin{gathered} m=\frac{1-4}{4-2} \\ \\ m=-\frac{3}{2} \end{gathered}\)it is an exponential function.
Ocean waves move in parallel lines toward the shore. The figure shows Sandy Beaches windsurfing across several waves. For this problem, think of Sandy’s wake as a line. m∠1 = (2x + 10)° and m∠2 = (4y − 30)°. Find x and y

Answers
Angle 2 is the same as the given angle of 70 degrees so we can solve for y:
4y-30 = 70
Add 30 to both sides:
4y = 100
Divide both sides by 4:
Y = 25
Angle 1 and angle two are supplementary angles and when added together need to equal 180:
We know angle 2 = 70, so angle 1 must equal 180-70 = 110
2x + 10 = 110
Subtract 10 from both sides:
2x = 100
Divide both sides by 2:
X = 50
The answer is:
X = 50, y = 25
If you look at the figure, the angle marked red is equal to 70° because vertical angles are equal. So, that also means that the opposite angle 2 is also 70°. So, the first equation is:
70 = 5x + y
Next, the green angle as marked is equal to
Green angle = 180 - 70 = 110
Being vertical angles, angle 1 is then equal to 110°. So,the second equation is
110 = 5x + 3y
Subtract the two equations:
5x + y = 70
- 5x + 3y = 110
________________
-3y = -40
y = -40/-3 = 13.33°
Substituting y to either one of the equations,
5x + 13.33 = 70
Solving for x,
x = 11.33°
Is. She analyzes
st.
Martha graphs the data for the number of bracelets made, a, and the number of beads used,
y, and draws a line through the points.
Number of Beads Used
600
500
400
300
200
100
0
Bracelets Made
versus Beads Used
(31, 651)
(23, 483).
(10, 210)
5 10 15 20 25 30 35
Number of Bracelets Made
Write an equation that represents the relationship between the number of bracelets made
and the number of beads used. Show or explain how you found the slope and y-intercept.
Enter your equation and your work or explanation in the space provided.
You may use the drawing box to add a drawing to help explain your answer.
A
7
44
▶
Exhibits
P
Answers
The equation for the relationship between the number of bracelets made and the number of beads is y = 21x.
First, the rate of change
= (483 - 210) / (23 - 10)
= 273 / 13
= 21
So, the equation for the relationship between the number of bracelets made and the number of beads used.
(y - 210) = 21 (x- 10)
y - 210 = 21x - 210
y = 21x
Learn more about Slope here:
https://brainly.com/question/3605446
#SPJ1
each friend received 5/4 of a pound of berries, how many friends are sharing berries?
Answers
Answer:
2
Step-by-step explanation:
If 5 friends are sharing the berries, how many pounds of berries does each friend receive? Is the answer to 3/4 divided by 2/5 greater than or less than 1.
what number line shows the solution of -5x + 10 > -15
Answers
Answer: x<5
Step-by-step explanation: Subtract 10 from both sides. Simplify -15-10 to -25. Divide both sides by -5. Two negatives make a positive. Simplify 25/5 to 5.
A certain freezing process requires that room temperature be lowered from 35oC at the rate of 6oC every hour. What will be the room temperature 8 hours after the process begins?
Answers
Answer:
-13 degrees celcius.
Step-by-step explanation:
6 degrees are lowered every hour. 6*8 = 48 degrees, 48 degrees are lowered.
35-48 is -13. The room temperature will be -13 eight hours after the process begins.
The cost of 24 pounds of cat food is $54. What is the cost per pound of cat food?
O $2.20
O $2.50
O $2.00
O $2.25
Answers
Answer:
$2.25
Step-by-step explanation:
To find the cost per pound you have to divide $54 by 24.
Graphs of a function and its inverse are shown on the same coordinate grid.
Which statements accurately compare the function and its inverse? Check all that apply.
The domains of the two functions extend to positive infinity.
The ranges of the two functions are all real numbers.
The x-intercept of f(x) and the y-intercept of f–1(x) are reciprocals of each other.
The point of intersection of the two functions indicates that the functions are inverses.
Neither function has a minimum.
Answers
The correct statements are;
The x-intercept of f(x) and the y-intercept of f–1(x) are reciprocals of each other.
The point of intersection of the two functions indicates that the functions are inverses.
Option C and D
How to determine the correct statementsTo accurately compare a function and its inverse based on the graphs, we have to know the following;
The domains of the two functions extend to positive infinity if the domain of the inverse function is equivalent to the range of the original function.The ranges of the two functions are all real numbers if the graphs cover the entire y-axis without any gaps or discontinuities.If the graphs intersect at the point (a, b), it means that f(a) = b and f^(-1)(b) = a, indicating that the functions are inverses of each other.
Learn more about functions at: https://brainly.com/question/11624077
#SPJ1
Please help Me I really need this !!!

Answers
Step-by-step explanation:
Original Equation:
\(x^2+5=0\)
Subtract 5 from both sides
\(x^2 = -5\)
Take the square root of both sides
\(x=\pm\sqrt{-5}\)
Simplify
\(x=\pm i\sqrt{5}\)
Thus we have two non-real solutions, and zero real solutions. This implies that the graph will never cross the x-axis when graphing the function out, because it has no real solutions.
Matthew invested $8,000 in an account paying an interest rate of 3 1/8% compounded
continuously. Parker invested $8,000 in an account paying an interest rate of 2 3/4%
compounded annually. To the nearest dollar, how much money would Parker have in
his account when Matthew's money has tripled in value?
Answers
Parker would have approximately $13,774 in his account when Matthew's money has tripled in value.
We have,
For Matthew's investment, the continuous compounding formula can be used:
\(A = P \times e^{rt}\)
Where:
A = Final amount
P = Principal amount (initial investment)
e = Euler's number (approximately 2.71828)
r = Annual interest rate (in decimal form)
t = Time (in years)
In this case,
Matthew's money has tripled,
So A = 3P.
For Parker's investment, the formula for compound interest compounded annually is used:
\(A = P \times (1 + r)^t\)
Where:
A = Final amount
P = Principal amount (initial investment)
r = Annual interest rate (in decimal form)
t = Time (in years)
We need to find t when Matthew's money has tripled in value.
Let's set up the equation:
\(3P = P \times e^{rt}\)
Dividing both sides by P, we get:
\(3 = e^{rt}\)
Taking the natural logarithm of both sides:
ln(3) = rt
Now we can solve for t
t = ln(3) / r
For Matthew's investment,
r = 3 1/8% = 3.125% = 0.03125 (as a decimal).
For Parker's investment,
r = 2 3/4% = 2.75% = 0.0275 (as a decimal).
Now we can calculate t for Matthew's investment:
t = ln(3) / 0.03125
Using a calculator, we find t ≈ 22.313 years.
Now, we can calculate how much money Parker would have in his account at that time:
\(A = P \times (1 + r)^t\)
\(A = $8,000 \times (1 + 0.0275)^{22.313}\)
Using a calculator, we find A ≈ $13,774.
Therefore,
Parker would have approximately $13,774 in his account when Matthew's money has tripled in value.
Learn more about compound interest here:
https://brainly.com/question/13155407
#SPJ1
Answer:
20,763
Step-by-step explanation:
I saw the answer after I got it wrong
When Alana was born, her grandma put $1000 into a money market account that earns 9% interest each year. How much will be in the account when Alana is 21?
Answers
The amount that would be in the account when Alana is 21 is $2890
How to determine the valueWe have to know the formula for simple interest.
This is expressed as;
S.I = PRT/100
Given that the parameters of the formula are enumerated as;
SI is the simple interestP is the principal amountR is the interest rateT is the time takenFrom the information given, substitute the values, we have;
SI = 1000 × 9 × 21/100
Multiply the values,
Then, divide by the denominator, we have;
SI = $1890
Learn more about simple interest at: https://brainly.com/question/20690803
#SPJ1
What is number 61 and a step by step explaination please?

Answers
1/3 ln(x) + ln(2) - ln(3) = 3
Recall that \(m\log_b(n)=\log_b(n^m)\), so
ln(x ¹ʹ³) + ln(2) - ln(3) = 3
Condense the left side by using sum and difference properties of logarithms:
\(\log_b(m)+\log_b(n)=\log_b(mn)\)
\(\log_b(m)-\log_b(n)=\log_b\left(\dfrac mn\right)\)
Then
ln(2/3 x ¹ʹ³) = 3
Take the exponential of both sides; that is, write both sides as powers of the constant e. (I'm using exp(x) = e ˣ so I can write it all in one line.)
exp(ln(2/3 x ¹ʹ³)) = exp(3)
Now exp(ln(x)) = x for all x, so this simplifies to
2/3 x ¹ʹ³ = exp(3)
Now solve for x. Multiply both sides by 3/2 :
3/2 × 2/3 x ¹ʹ³ = 3/2 exp(3)
x ¹ʹ³ = 3/2 exp(3)
Raise both sides to the power of 3:
(x ¹ʹ³)³ = (3/2 exp(3))³
x = 3³/2³ exp(3×3)
x = 27/8 exp(9)
which is the same as
x = 27/8 e ⁹
let C be the curve y=5sqrtx for 1.1

Answers
We can integrate this S = 2π ∫(1.1 to 4.4) (5√(4x + 25))/(2√x) dx over the given interval (1.1 to 4.4) to find the surface area.
We can evaluate the integral using numerical methods or a calculator to find the final answer.
We have,
To find the surface area of the revolution about the x-axis of the function f(x) = 5√x over the interval (1.1 to 4.4), we can use the formula for the surface area of revolution:
S = ∫(a to b) 2πy√(1 + (f'(x))²) dx
In this case,
f(x) = 5√x, so f'(x) = (d/dx)(5√x) = 5/(2√x).
Let's calculate the surface area:
S = ∫(1.1 to 4.4) 2π(5√x)√(1 + (5/(2√x)²) dx
Simplifying the expression inside the integral:
S = ∫(1.1 to 4.4) x 2π(5√x)√(1 + 25/(4x)) dx
Next, we can integrate this expression over the given interval (1.1 to 4.4) to find the surface area.
To find the surface area of revolution about the x-axis of the function
f(x) = 5√x over the interval (1.1 to 4.4), we need to evaluate the integral:
S = ∫(1.1 to 4.4) 2π(5√x)√(1 + 25/(4x)) dx
Let's calculate the integral:
S = 2π ∫(1.1 to 4.4) (5√x)√(1 + 25/(4x)) dx
To simplify the calculation, let's simplify the expression inside the integral first:
S = 2π ∫(1.1 to 4.4) (5√x)√((4x + 25)/(4x)) dx
Next, we can distribute the square root and simplify further:
S = 2π ∫(1.1 to 4.4) (5√(4x + 25))/(2√x) dx
Thus,
We can integrate this expression over the given interval (1.1 to 4.4) to find the surface area.
We can evaluate the integral using numerical methods or a calculator to find the final answer.
Learn more about the surface area of revolutions here:
https://brainly.com/question/32268747
#SPJ1
Question Help The mean finish time for a yearly amateur auto race was 185.64 minutes with a standard deviation of 0.314 minute. The winning car, driven by Sam, finished in 185.29 minutes. The previous year's race had a mean finishing time of 110.3 with a standard deviation of 0.129 minute. The winning car that year, driven by Rita, finished in 110.02 minutes. Find their respective z-scores. Who had the more convincing victory?
Answers
Answer:
Sam has the more convincing victory with a greater Zscore value
Step-by-step explanation:
Given that :
Year 1:
Mean finish time (m) = 185.64
Standard deviation (s) = 0.314
Sam's time (x1) = 185.29
Year 2:
Mean finish time (m) = 110.3
Standard deviation (s) = 0.129
Rita's time (x1) = 110.02
Zscore = (x - mean) / standard deviation
Sam's Zscore :
(185.29 - 185.64) / 0.314
= - 0.35 / 0.314
= −1.114649
= - 1.115
Rita's Zscore :
(110.02 - 110.3) / 0.129
= - 0.28 / 0.129
= −2.170542
= - 2.171
Sam has the more convincing victory with a greater Zscore value
[1] 2 (a) Using the information given in the advertisement shown, find the sale price of the table. Answer.... SALE All prices reduced by 30% Save $180 on this table
Answers
Based on the information given in the advertisement, we can conclude that the sale price of the table is $420.
Here's how we can arrive at this answer:
Let the original price of the table be represented by P.
We know that the sale price of the table is obtained by reducing the original price by 30%. Mathematically, this can be represented as:
Sale price = P - 0.3P
Simplifying this expression, we get:
Sale price = 0.7P
We are also given that the sale saves us $180 on this table. Mathematically, this can be represented as:
0.7P - P = -$180
Simplifying this expression, we get:
-0.3P = -$180
Dividing both sides by -0.3, we get:
P = $600
Therefore, the original price of the table was $600.
Using the equation for sale price that we derived earlier, we can now find the sale price of the table:
Sale price = 0.7P = 0.7 x $600 = $420
Hence, the sale price of the table is $420.
Consider this function.
f(x) = |x – 4| + 6
If the domain is restricted to the portion of the graph with a positive slope, how are the domain and range of the function and its inverse related?
Answers
If we restrict the domain of the function to the portion of the graph with a positive slope, the domain of the inverse function will be the range of the original function for values of x greater than 4, and its range will be all real numbers greater than or equal to 4.
The given function f(x) = |x – 4| + 6 is a piecewise function that contains an absolute value. The absolute value function has a V-shaped graph, and the slope of the graph changes at the point where the absolute value function changes sign. In this case, that point is x=4.
If we restrict the domain of f(x) to the portion of the graph with a positive slope, we are essentially considering the piece of the graph to the right of x=4. This means that x is greater than 4, or x>4.
The domain of the inverse function, f⁻¹(x), will be the range of the original function f(x) for values of x greater than 4. This is because the inverse function reflects the original function over the line y=x. So, if we restrict the domain of f(x) to values greater than 4, the reflected section of the graph will be the range of f⁻¹(x).
The range of f(x) is all real numbers greater than or equal to 6 because the absolute value function always produces a positive or zero value and when x is greater than or equal to 4, we add 6 to that value. The range of f⁻¹(x) will be all real numbers greater than or equal to 4, as this is the domain of the reflected section of the graph.
for more such questions on domain
https://brainly.com/question/2264373
#SPJ8
The product of two negative integers is a negative integer.
Answers
Answer:
False. The product of two negative integers is a positive integer.
18. Graph the system of inequalities.
2x + y 21
x + 3y <-3
у
Name two points that are solutions to the system.
10
810
x
-10
End

Answers
Answer:
Graph the system of inequalities. 2x + y 21 x + 3y <-3 у Name two points that are solutions .
Find the equation that represents the relationship between the variables.

Answers
to get the equation of any straight line, we simply need two points off of it, hmmm let's use (0 , 10) and (8 , 30) from the table
\((\stackrel{x_1}{0}~,~\stackrel{y_1}{10})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{30}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{30}-\stackrel{y1}{10}}}{\underset{run} {\underset{x_2}{8}-\underset{x_1}{0}}}\implies \cfrac{20}{8}\implies \cfrac{5}{2}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{10}=\stackrel{m}{\cfrac{5}{2}}(x-\stackrel{x_1}{0}) \\\\\\ y-10=\cfrac{5}{2}x\implies y=\cfrac{5}{2}x+10\)
Which sum or difference is modeled by the algebra tiles?
Answers
As a result, choice C is the equation that best represents the algebraic tiles since we only need to determine the total or difference.
what is expression ?It is possible either multiply, distribute, add, or negate in mathematics. The trying to follow is how a expression is put together: Number, expression, and scientific operator The ingredients of a mathematical expression include numbers, variables, and operations (such as addition, subtraction, multiplication or division etc.) It is possible to combine expressions and phrases. An expressions, often known as an arithmetic operation, is any mathematical statement that contains variables, numerals, and a numerical operation between them. That instance, the word m there in given equation is separated from the terms 4m and 5 by the arithmetic symbol +, as is the variable m in the phrase 4m + 5.
given
To address this issue, we just need to determine the total or difference that yields 2x2 + 2x + 2
Option A: ( x2 + 4x -2) + (x2 - 2x - 4) = 2x2 + 2x - 6
Option B: ( x2 + 4x - 2 ) + ( x2 + 2x + 4 ) = 2x2 + 6x + 2
Option C: ( x2 + 4x - 2) - ( -x2 + 2x - 4)= x2 + 4x - 2 + x2 - 2x + 4
= 2x2 + 2x + 2
As a result, choice C is the equation that best represents the algebraic tiles since we only need to determine the total or difference.
To know more about expressions visit :-
brainly.com/question/14083225
#SPJ1
The complete question is:-
Select the correct answer.
Which sum or difference is modeled by the algebra tiles?
A. (-x2 + 2x + 3) − (x2 − 2x − 1) = -2x2 + 2
B. (-x2 + 2x + 3) − (-x2 + 2x + 1) = -2x2 + 2
C. (-x2 + 2x + 3) + (-x2 + 2x + 1) = -2x2 + 2
D. (-x2 + 2x + 3) + (-x2 − 2x − 1) = -2x2 + 2
Factors 3x^4-5x^3+6x^2-15x completely over the set of integers

Answers
The Factors of 3x^4-5x^3+6x^2-15x completely over the set of integers will give 5(1-3x).
How can this be calculated?In mathematics, factorization or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller
The expression can be broken down after the other as
[2x4 = 8] + [5x3=15] + [6x2=12]
= [8-15+12-15x]
=5-15x
then we can factorize as
5(1-3x)
Learn more about integers at:
https://brainly.com/question/17695139
#SPJ1
Please please please please help