The United States Capitol is
located at (2, 4) on a coordinate grid. The White
House is located at (-10, 16) on the same coordinate
grid. Find two different points on a segment joining
the United States Capital and the White House such
that the ratio of the two shorter segments created by
each point is 1:3.
Answers
Answer:
The two different point on a segment joining the United States Capital and the White House such that the ratio of the shorter segments created by each is 1 : 3 are \(\vec C_{1} =(-1,7)\) and \(\vec C_{2} = (-7,13)\).
Step-by-step explanation:
At first we need to calculate the vector distance between \(A(x,y) = (2, 4)\) and \(B(x,y) =(-10,16)\) by following vectorial subtraction:
\(\overrightarrow{AB} = \vec B - \vec A\) (Eq. 1)
Where:
\(\overrightarrow{AB}\) - Vector distance between points A and B, dimensionless.
\(\vec A\), \(\vec B\) - Vector distance between each point and origin, dimensionless.
If we know that \(A(x,y) = (2, 4)\) and \(B(x,y) =(-10,16)\), then we have the following result:
\(\overrightarrow {AB} = (-10,16)-(2,4)\)
\(\overrightarrow{AB} = (-10-2,16-4)\)
\(\overrightarrow{AB} = (-12,12)\)
Besides, we can find the location of any point inside the line segment by using the following vectorial equation:
\(\vec C = \vec A + r\cdot \overrightarrow{AB}\) (Eq. 2)
Where:
\(r\) - Segment factor, dimensionless.
\(\vec C\) - Location of resulting point, dimensionless.
There are two different options for the location of resulting point: \(r_{1} = \frac{1}{4}\) and \(r_{2} = \frac{3}{4}\). Now we proceed to find each option:
\(r_{1} = \frac{1}{4}\)
\(\vec C_{1} = (2,4) +\frac{1}{4}\cdot (-12,12)\)
\(\vec C_{1} = (2,4)+(-3,3)\)
\(\vec C_{1} =(-1,7)\)
\(r_{2} = \frac{3}{4}\)
\(\vec C_{2} = (2,4) +\frac{3}{4}\cdot (-12,12)\)
\(\vec C_{2} = (2,4) +(-9,9)\)
\(\vec C_{2} = (-7,13)\)
The two different point on a segment joining the United States Capital and the White House such that the ratio of the shorter segments created by each is 1 : 3 are \(\vec C_{1} =(-1,7)\) and \(\vec C_{2} = (-7,13)\).
Related Questions
What is the best answer to report for (515 x 0.0025) +24.57? A. 25.858. B. 25.85.
C. 25.8575. D. 26. E. 25.9
Answers
The best answer to submit for (515 x 0.0025) + 24.57 is 25.8575.
A decimal is a number with a whole and a fractional component. Decimal numbers, which are in between integers, are used to express the numerical value of full and partially whole amounts. Decimal notation is the name for the method used to represent numbers in the decimal system. The Hindu-Arabic numeral system has been expanded to include non-integer values.
To find the answer to the expression (515 x 0.0025) +24.57, we can simplify it by performing the multiplication and addition in the correct order:
(515 x 0.0025) + 24.57 = 1.2875 + 24.57 = 25.8575
Therefore, the best answer to report is C. 25.8575.
For more questions on Decimal Numbers
https://brainly.com/question/28579947
#SPJ4
please help me with this it's a huge test :) i'll mark brainliest!
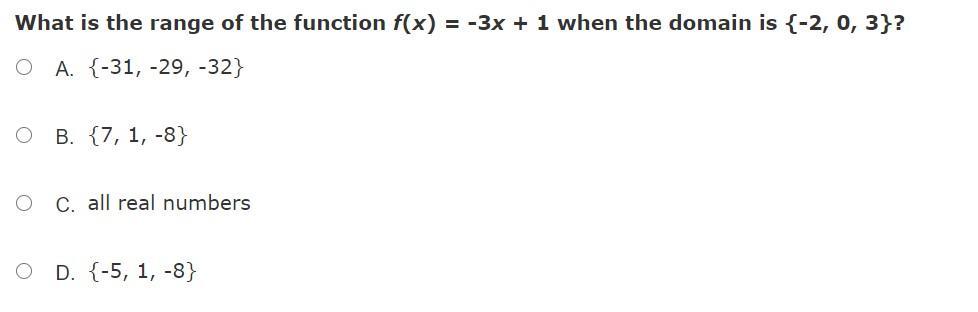
Answers
Answer:
I think A or D
Step-by-step explanation:
the diagram shows a cuboid 4cm, 5cm and 9cm what is the surface area of the cuboid?
Answers
length= 9 cm
width= 5 cm
height= 4 cm
to find:the surface area of the given cuboid.
solution:\(s.a = 2(lb + bh + lh)\)
\(s.a = 2((9 \times 5) + (5 \times 4) + (9 \times 4))\)
\(s.a = 2(45 + 20 + 36)\)
\(s.a = 2 \times 101\)
\(s.a = 202 \: {cm}^{2} \)
therefore, the surface area of the given cuboid is 202 square centimeters.
how much is 173 cm to feet?
Answers
Answer:
5 feet and 6 inches
Step-by-step explanation:
E15 gasoline contains 15% of alcohol calculate the volume in liters of alcohol in a full 20 gallon gas tank
Answers
Since, 1 gallon = 3.78541 liters
Therefore, 20 gallons = 75.7082 liters
That means amount of gasoline in the gas tank is 20 gallons or 75.7082 liters.
It's given in the question that E15 gasoline contains 15% of alcohol.
Therefore, amount of alcohol in the gas tank = 15% of 75.7082
= 11.35623
≈ 11.36 liters
Learn more,
https://brainly.com/question/618776
Amount of total Alcohol in liters is 11.355 liter.
Given:
Amount of total gas solution = 20 gallon
Amount of Alcohol in total gas = 15%
Find:
Amount of total Alcohol in liters
Computation:
1 Gallon = 3.785 liter (Approx.)
Amount of total gas solution in liter = 20 × 3.785
Amount of total gas solution in liter = 75.7 liter (Approx.)
Amount of total Alcohol in liters = Amount of total gas solution in liter × Amount of Alcohol in total gas
Amount of total Alcohol in liters = 75.7 × 15%
Amount of total Alcohol in liters = 75.7 × 0.15
Amount of total Alcohol in liters = 11.355 liter (Approx.)
Learn more:
https://brainly.com/question/1578538?referrer=searchResults
Five employees are available to perform four jobs. The lime it takes each person to perform each job is given in Table 50. Determine the assignment of employees to jobs that minimizes the total time required to perform the four jobs.
TABLE 50
Person
Time (hours)
Job 1
Job 2
Job 3
Job 4
1
22
18
30
18
2
18
—
27
22
3
26
20
28
28
4
16
22
—
14
5
21
—
25
28
Answers
To determine the assignment of employees to jobs that minimizes the total time required to perform the four jobs, we need to consider the time taken by each person to complete each job. Using the given Table 50, we can analyze the data and identify the optimal assignment.
By examining Table 50, we can identify the minimum time taken by each person for each job. Starting with Job 1, we see that Person 4 takes the least time of 16 hours. Moving to Job 2, Person 2 takes the least time of 18 hours. For Job 3, Person 1 takes the least time of 25 hours. Lastly, for Job 4, Person 4 takes the least time of 14 hours.
Therefore, the optimal assignment would be:
- Person 4 for Job 1 (16 hours)
- Person 2 for Job 2 (18 hours)
- Person 1 for Job 3 (25 hours)
- Person 4 for Job 4 (14 hours)
This assignment ensures that the minimum total time is required to perform the four jobs, resulting in a total time of 16 + 18 + 25 + 14 = 73 hours.
To learn more about minimize total time click here: brainly.com/question/15071332
#SPJ11
Un fabricante de carteras de la marca "C&L" vende cada cartera a su distribuidor argentino al precio de (230 - q) soles si la cantidad q es menor que 210. Si el costo unitario de cada cartera es S / 20 y el monto de los costos fijos a S / 2,000. A. Determine las ecuaciones de ingreso y costo total para el fabricante al producir y vender carteras q. Si. Determine la ecuación de utilidad del fabricante al vender q unidades de carteras. C. ¿Cuántas carteras se distribuirán, si la ganancia obtenida es de 1800 soles, sabiendo que es mayor que 50? D concentración
Answers
Answer:
A. 101 × q / 2000 S
B. Ingresos totales de q unidades = 230 · q - q²
Costo total para producir q unidades = 101 × q / 2000 S
C. 222 carteras
Step-by-step explanation:
A. Ingresos totales = q × (230 - q) = 230 · q - q²
El costo unitario = S / 20
El costo fijo = S / 2000
Costo total para producir q unidades = q × (S / 20 + S / 2000) = 101 × q / 2000 S
B. Las ganancias totales = Ingresos totales- Costo total
Las ganancias totales = 230 · q - q² - 101 · q / 2000
Las ganancias totales = 229.9495 · q - q²
C, cuando las ganancias obtenidas = 1800 soles, tenemos;
1800 = 229.9495 · q - q²
q² -229.9495 + 1800 = 0
(q - 8.114) × (q - 221.84) = 0
Por lo tanto, q = 8.114 o q = 221.84
Por lo tanto, sabemos que q> 50, por lo tanto, el valor correcto de q = 221.84 o 222 carteras.
Write the slope-intercept form of the equation of each line given the slope and y-intercept.
Slope= -10/3, y- intercept=5
Answers
Answer:
y = -10/3x + 5
Step-by-step explanation:
Hi there!
We are given that a line has a slope of -10/3, and a y intercept of 5
We want to write the equation of this same line in slope-intercept form, which is y=mx+b, where m is the slope and b is the y intercept
As we are already given the slope and y intercept, we can simply substitute these values into the format for slope-intercept form to find the equation of the line!
Starting with the slope, substitute -10/3 as m in y=mx+b
y = -10/3x + b
Now for the y intercept, substitute 5 as b in the equation
y = -10/3x + 5
Hope this helps!
See more on this topic here: https://brainly.com/question/17788099
an architect draws a plan for a wheelchair ramp on the plan, the ramp is 2cm high and 24cm long what might the dimensions of the actual ramp be
Answers
Answer:
Step-by-step explanation:
Check all properties that the following relations on the set of positive integers have. The relations are defined by (x,y)∈R if and only if the indicated condition is satisfied.
a. x and y have a common prime factor
1. symmetric
2. reflexive
3. transitive
4. antisymmetric
5. irreflexive
b. x−y is a multiple of 3
1. irreflexive
2. reflexive
3. transitive
4. symmetric
5. antisymmetric
Answers
The relations are defined by (x,y)∈R is antisymmetric.
The given sets of relations on the set of positive integers are (x,y) ∈ R if and only if the following conditions are met:a. x and y have a common prime factor1. Symmetric2. Reflexive3. Transitive4. Antisymmetric5. Irreflexiveb. x-y is a multiple of 31. Irreflexive2. Reflexive3. Transitive4. Symmetric5. Antisymmetric
Let's prove the above property one by one.(a) x and y have a common prime factor1. SymmetricLet's suppose (x, y) ∈ R such that x and y have a common prime factor. This implies that y and x also have a common prime factor. So, (y, x) ∈ R. Hence, R is symmetric.2. Reflexive Let's assume that x is a positive integer.
Then, x and x have a common prime factor, that is, x itself. Thus, (x, x) ∈ R. Hence, R is reflexive.3. TransitiveLet's assume that (x, y) ∈ R and (y, z) ∈ R. This means that x and y have a common prime factor, and y and z have a common prime factor.
So, x and z have a common prime factor too, since the greatest common divisor of a set of numbers is also a divisor of every linear combination of them. Thus, (x, z) ∈ R. Therefore, R is transitive.4. AntisymmetricLet's assume that (x, y) ∈ R and (y, x) ∈ R.
This implies that x and y have a common prime factor, and y and x have a common prime factor, respectively. Thus, x and y are the same integers. Hence, R is antisymmetric.5. IrreflexiveLet's assume that x is a positive integer, and (x, x) ∈ R. This implies that x and x have a common prime factor, which is x.
Thus, x/x = 1 is also a common prime factor, but this contradicts the fact that the set of common prime factors of a pair of integers is non-empty and must not contain 1. Therefore, R is irreflexive.(b) x - y is a multiple of 31. IrreflexiveLet's assume that x is a positive integer. Then, x - x = 0 is not a multiple of 3.
Therefore, (x, x) is not in R. Hence, R is irreflexive.2. ReflexiveLet's assume that x is a positive integer. Then, x - x = 0 is a multiple of 3. Therefore, (x, x) ∈ R. Hence, R is reflexive.3. TransitiveLet's assume that (x, y) ∈ R and (y, z) ∈ R. This means that x - y is a multiple of 3 and y - z is also a multiple of 3.
So, x - z = (x - y) + (y - z) is a multiple of 3, since the sum of multiples of 3 is a multiple of 3. Therefore, (x, z) ∈ R. Hence, R is transitive.4. SymmetricLet's assume that (x, y) ∈ R. This implies that x - y is a multiple of 3. Thus, y - x = - (x - y) is also a multiple of 3. Therefore, (y, x) ∈ R. Hence, R is symmetric.5. Antisymmetric
Let's assume that (x, y) ∈ R and (y, x) ∈ R. This implies that x - y is a multiple of 3, and y - x is also a multiple of 3. Thus, x - y = y - x, or x = y. Therefore, R is antisymmetric.
To know more about antisymmetric refer here:
https://brainly.com/question/31425841#
#SPJ11
Select the two values of x that are roots of this equation.
2x-5=-3x2
Answers
Answer:
Step-by-step explanation:

Use inductive and deductive reasoning to solve the problem. Draw a diagram and solve the problem Freddie the frog is a at the bottom of a 30- foot wall. Each day he jumps up 3 feet. Each night he slides back down 2 feet. How many days will it take Freddie to get on top of the wall ?
Answers
Answer:
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
Step-by-step explanation:
Determine whether the value given below is from a discrete or continuous data set
When a car is randomly selected and weighed it is found to weigh 1628.3 kg.
a. A discrete data set because there are infinitely many possible values
b. A discrete data set because the possible values can be counted
c. A continous data set because the possible values can be counted
d. A continous data set because there are infinitely many possible values
Answers
The value given is from a continuous data set because there are infinitely many possible values.
In statistics, a discrete data set is a set of data that can only take certain values, typically whole numbers, that can be counted. A continuous data set is a set of data that can take any value within a certain range, and the values can't be counted as they are infinite in number.
In the given scenario, the weight of a car can take any value within a certain range, and there are infinitely many possible values between any two values. For example, between 1628.3 kg and 1628.4 kg, the car's weight could be an infinite number of values. Hence, the weight of the car is a continuous variable, and the given value of 1628.3 kg is part of a continuous data set.
Hence, the correct answer is d.
To know more about continuous data set, here
https://brainly.com/question/13421250
#SPJ4
HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP
HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP HELP I NEED HELP ASAP

Answers
Answer:
The answer should be A I think
A man is trapped in a room at the center of a maze. The room has three exits. Exit 1 leads outside the maze after 3 minutes, on average. Exit 2 will bring him back to the same room after 5 minutes. Exit 3 will bring him back to the same room after 7 minutes. Assume that every time he makes a choice, he is equally likely to choose any exit. What is the expected time taken by him to leave the maze?Hint: Let X = time taken by the man to leave the maze from this room. Let Y = exit he chooses first. So Y belongs in { 1,2,3} Calculate the conditional expectation of time taken to leave the maze given that he chose each of the exits. Then use these conditional expectations to calculate the expectation of time taken to leave the maze.
Answers
The expected time taken by the man to leave the maze is 15 minutes.
To find the expected time taken by the man to leave the maze, we'll first calculate the conditional expectation of time taken given that he chose each of the exits, and then use these conditional expectations to calculate the overall expectation.
Step 1: Calculate the conditional expectations :
- If he chooses Exit 1 (probability 1/3), he leaves the maze after 3 minutes.
- If he chooses Exit 2 (probability 1/3), he returns to the same room after 5 minutes and starts again. So, the expected time in this case is 5 + E(X).
- If he chooses Exit 3 (probability 1/3), he returns to the same room after 7 minutes and starts again. So, the expected time in this case is 7 + E(X).
Step 2: Calculate the overall expectation :
E(X) = (1/3)*(3) + (1/3)*(5 + E(X)) + (1/3)*(7 + E(X))
Now, we'll solve for E(X):
3E(X) = 3 + 5 + 7 + 2E(X)
E(X) = 15 minutes
The expected time taken by the man to leave the maze is 15 minutes.
To learn more about conditional probability visit : https://brainly.com/question/30760899
#SPJ11
According to the problem, there are three possible exits (1, 2, and 3) from the room in the center of the maze. The probabilities of choosing each of these exits are equal.
Exit 1 leads to the outside of the maze, and it takes 3 minutes on average to reach it. Exit 2 leads back to the same room, so the man will need to start over again. Exit 3 also leads back to the same room, and it takes longer than exit 2 to get there (7 minutes).Let X be the time taken by the man to leave the maze from this room. Let Y be the exit he chooses first. Y belongs to {1, 2, 3}. Calculate the conditional expectation of the time taken to leave the maze given that he chose each of the exits. Then use these conditional expectations to calculate the expectation of the time taken to leave the maze.The expected value of X can be calculated as follows:() = ( | = 1) × ( = 1) + ( | = 2) × ( = 2) + ( | = 3) × ( = 3)Expected time to leave the maze through exit 1:( | = 1) = 3Expected time to leave the maze through exit 2:( | = 2) = 5 + ()Expected time to leave the maze through exit 3:( | = 3) = 7 + ()The probability of choosing each exit is 1/3, so:P(Y = 1) = 1/3P(Y = 2) = 1/3P(Y = 3) = 1/3Substituting these values into the equation for ():() = 3(1/3) + (5 + ())(1/3) + (7 + ())(1/3)() = 5 + (2/3)() + (7/3)()() = 15 minutes. Therefore, the expected time taken by the man to leave the maze is 15 minutes.
Learn More About Conditional Expectation: https://brainly.com/question/23382435
#SPJ11
Joe’s Coffee is having a stained glass window installed on their front door. Approximately how much glass will be needed to create the stained glass window?
PLSS USE STEPSSS!!!!
A) 2.4
B) 9.6
C) 11
D) 38.5
Answers
\(\color{plum}\tt \: D) 38.5 \)
Steps to derive correct answer :Diameter of the stained glass window Joey needs = 3.5
Area of the window = quantity of glass Joey needs
Area of the window :
\( = \tt\pi {r}^{2} \)
\( = \tt3.14 \times 3.5 \times 3.5\)
\( =\tt 3.14 \times 12.25\)
\( =\tt 38.46\)
38.46 can be rounded off to 38.5.
Therefore, quantity of glass needed to make the stained glass window = 38.5
what is 8 1/3x6 3/4=
Answers
Answer:
I think it is 56.25 not sure but try it
Answer:
56.25 or 56\(\frac{1}{4}\)
Step-by-step explanation:
First:
Convert any mixed numbers to fractions.
Then your initial equation becomes:
\(\frac{25}{3}\) × \(\frac{27}{4}\)
Applying the fractions formula for multiplication,
\(\frac{25}{3}\) × \(\frac{27}{4}\)
\(\frac{675}{12}\)
Simplifying 675/12, the answer is
56\(\frac{1}{4}\)
Micah is saving for a new skateboard. It costs $65, including tax. Micah has already saved $37. What in the equation?
Answers
Answer:
x + 37 ≥ 65
Step-by-step explanation:
Given:
Money Micah wants = $65
Money Micah had = $37
Find:
Money Micah need
Computation:
Money Micah need(x)
x + 37 ≥ 65
So,
Money Micah need = 65 - 37
Money Micah need = $28
Circles with centers $A$ and $B$ have radii 3 and 8, respectively. A common internal tangent touches the circles at $C$ and $D$, as shown. Lines $AB$ and $CD$ intersect at $E$, and $AE
Answers
The length of line segment $BC$, which is the hypotenuse of a right triangle with legs of length 5.41 and 11, is 13.93.
Let AB = x.
Then, using the Pythagorean Theorem, we have:
\($$x^2 + (3+8)^2 = (x+11)^2$$$$x^2 + 19^2 = (x+11)^2$$$$x^2 + 361 = x^2 + 242 + 22x$$$$22x = 119$$$$x = \frac{119}{22} = 5.41$$Therefore, $BC = x+11 = 5.41 + 11 = 16.41$.\)
Let $AB = x$. We can use the Pythagorean Theorem to determine the length of $AB$. Since $A$ and $B$ are the endpoints of $AB$, the length of $AB$ is the hypotenuse of a right triangle with two legs of length 3 and 8. Therefore, we have:
\($$x^2 = 3^2 + 8^2 = 9 + 64 = 73$$$$x = \sqrt{73} = 8.54$$\)
Now that we know the length of AB, we can use it to calculate the length of BC. Since BC is the hypotenuse of a right triangle with legs of length x and 11, we have:
\($$BC^2 = x^2 + 11^2$$$$BC^2 = 8.54^2 + 11^2$$$$BC^2 = 73.14 + 121$$$$BC^2 = 194.14$$$$BC = \sqrt{194.14} = 13.93$$\)
Therefore, the length of BC is 13.93.
The complete question is: Circles with centers A and B have radii 3 and 8, respectively. A common internal tangent touches the circles at C and D, as shown. Lines AB and CD intersect at E, and AE is perpendicular to BC. Find the length of BC.
Learn more about length here
https://brainly.com/question/13194650
#SPJ4
What value for x will make the equation −3x+1=2(4x−5)true?
Answers
I need help please!!!

Answers
Answer:
B
Step-by-step explanation:
i believe the answer is B because C and D don't make sense in the context of the problem
Highlight the major milestones in mathematics from Euclid to Euler.
Answers
The major milestones in mathematics from Euclid to Euler are shown below.
Here are some major milestones in mathematics from Euclid to Euler:
1. Euclid (circa 300 BCE):
Euclid's Elements: Euclid wrote a comprehensive mathematical treatise called "Elements.
2. Archimedes (circa 287 BCE - 212 BCE):
Archimedes' Principle: He formulated the principle of buoyancy, known as Archimedes' Principle, which states that an object submerged in a fluid experiences an upward force equal to the weight of the displaced fluid.
3. Leonardo Fibonacci (1170 - 1250):
Fibonacci Numbers: Fibonacci introduced the concept of Fibonacci numbers, a sequence in which each number is the sum of the two preceding ones (e.g., 0, 1, 1, 2, 3, 5, 8, ...).
4. René Descartes (1596 - 1650):
Cartesian Coordinate System: Descartes developed the Cartesian coordinate system, which allows for the representation of geometric figures and algebraic equations using a set of axes.
5. Isaac Newton (1642 - 1727) and Gottfried Wilhelm Leibniz (1646 - 1716):
Calculus: Newton and Leibniz independently developed calculus, a branch of mathematics that deals with rates of change and the calculation of areas and volumes.
6. Leonhard Euler (1707 - 1783):
Euler's Formula: Euler made numerous contributions to mathematics, including the development of graph theory and the discovery of many important mathematical relationships. One of his notable achievements is Euler's formula, which relates the number of vertices, edges, and faces of a polyhedron.
Learn more about Mathematicians here:
https://brainly.com/question/28191378
#SPJ1
Help!
Explain how to employ the Pythagorean theorem in calculating the volume of a right cylinder if you know the distance from the edge of the base to the center of the top along with either its radius or its height.
Answers
To use the Pythagorean theorem to calculate the volume of a right cylinder, you would first need to know the radius of the base and the height of the cylinder. Once you have those two measurements, you can use the Pythagorean theorem to calculate the distance from the edge of the base to the center of the top.
The formula for the volume of a cylinder is V = πr^2h where r is the radius of the base and h is the height of the cylinder.
So if you know the distance from the edge of the base to the center of the top along with either its radius or its height, you can use the Pythagorean theorem to calculate the missing measurement and then use the formula for the volume of a cylinder to calculate the volume.
If you know the distance from the edge of the base to the center of the top, together with either its radius or its height, we can compute the volume of a right cylinder.
What is the Pythagorean theorem?In a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides, according to Pythagoras's Theorem. The theorem can be used to determine how steep mountains or slopes are. To calculate the distance between an observer and a location on the ground when the observer is looking down from a tower or structure. It is mostly utilized in the construction industry.
Note that h refers to half of the total height of the cylinder. I chose to use
h instead of h/2 to simplify things later on.
To find the volume of our cylinder, we need to multiply the area of the top by the total height of the cylinder. In other words;
V = pi * (radius of cylinder)² (height of cylinder)
V = pi(r² - h²) 2h
V = 2pi h(r² - h²)
This is our volume function. Next, we take the derivative of the volume function and set it equal to zero. If we move the h inside the parenthesis, we only need to use the power rule to get the derivative.
d/dxV(h) = 2pi(r² -3 h²) = 0
The 2π divides out and we are left with;
r² − 3h²=0
After some rearranging;
h² = r²/3
Take the square root of both sides.
h = r/√3
That is how we can calculate the volume of a right cylinder, if you know the distance from the edge of the base to the center of the top along with either its radius or its height.
Learn more about Pythagorean theorem here:
https://brainly.com/question/10174253
#SPJ1
Please help me
Write an equation to represent the following statement
j is 14 less than 22.
Solve for j.
j =

Answers
Answer:
J is 8. (J= 22-14) So that would simplify to (J= 8)
Step-by-step explanation:
hope this helps :)
J is 8. (J= 22-14) So that would simplify to (J= 8)
A bug begins to crawl up a vertical wire at time t = 0. The velocity v of the bug at time t, 0 < t < 8, is given by the function whose graph is shown behind this text. At what value of t does the bug change direction? a. 2
b. 4
c. 6.5
d. 7
Answers
The bug changes direction at t = 4. This can be answered by the concept of velocity.
To determine when the bug changes direction, we need to find when its velocity changes sign from positive to negative. From the graph, we see that the bug's velocity is positive for t < 4 and negative for t > 4. Therefore, the bug changes direction at t = 4.
To verify this, we can look at the behavior of the bug's velocity as it approaches t = 4. From the graph, we see that the bug's velocity is increasing as it approaches t = 4 from the left, and decreasing as it approaches t = 4 from the right. This indicates that the bug is reaching a maximum velocity at t = 4, which is when it changes direction.
Therefore, the bug changes direction at t = 4.
To learn more about velocity here:
brainly.com/question/18084516#
#SPJ11
Help needed ASAP will give BRAINLIEST not a real test

Answers
Answer:
I believe the answer is $1702.50.
Step-by-step explanation:
If you multiply 1500 by 4.5% (0.045 as a decimal) you will get 67.5 which is $67.5 interest for one year. For three years, you have too multiply 67.5 by 3 and you get $202.5. Finally, you add the total interest to the starting amount, $1500, which results in $1702.50.
Given the points (7,3) and (k,−7), for which values of k would the distance between the points be 2√ 41 ?A. 17 or -4B. 17 or 2C. 15 or -1D. 14 or -4
Answers
For this problem, we use the formula for the distance between two points:
\(d((x_1,y_1),(x_2,y_2))=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}\)Substituting the given points, setting the distance equal to 2√41, and solving for k we get:
\(\begin{gathered} 2\sqrt[]{41}=\sqrt[]{(k-7)^2+(-7-3)^2}=\sqrt[]{k^2-14k+49+100} \\ 2\sqrt[]{41}=\sqrt[]{k^2-14k+149} \\ k^2-14k+149=4\cdot41=164 \\ k^2-14k+49=64 \\ (k-7)^2=8^2 \\ k-7=8\text{ or k-7=-8} \\ k=15\text{ or k=-1} \end{gathered}\)Find the Surface area of the trapezoid
please help
show work

Answers
Answer:
259.5
Step-by-step explanation:
8.1*12=97.2
Area of trapiezium = 1/2(b+a)h
(2.8+8.1)=10.9
10.9*3/2=16.35
16.35*2=32.7
2.8*12=33.6
33.6+32.7+97.2=163.5
4*12*2=96
163.5+96=259.5
(03.01 LC) The LCM of 8 and 10 is _______. (
Answers
Answer:
Step-by-step explanation:
1. Definition of Least common multiple: The least common multiple of two numbers is the smallest number that is a multiple of both of the numbers
2. Find the LCM 8 and 10=
Multiplies of 8= 8,16,24,32,40....
Multiplies of 10= 10,20, 30,40 ,50....
3. We found it!
40 is the least common multiple!
............................

Answers
Answer:
8.63
Step-by-step explanation:
It ends in a one and it has to end in the 100ths place sooo.... yeah
Hope this helps!