the product of 6 and 11 written as an algebraic expression
Answers
Answer:
(2×3)¹
(11×1)¹
Step-by-step explanation:
2×3=6 so 2 to the power 1 is 2 and 3 to the power 1 is 3 so 2×3=6
11×1=11 so 11 to the power 1 is 11 and 1 to the power 1 is 1 so 11×1 =11
Related Questions
If l is parallel to m, solve for x and y.

Answers
Answer:
x=17, y=9
Step-by-step explanation:
(5x - 38)° = (3x - 4)°
2x = 34
x=17
(5(17)-38))=47
90°+47°+(7y-20)=180°
7y-20=43°
y=9
The value of x is 17 and y is 9.
What are the properties of parallel lines?Following are the properties of parallel lines,
The pairs of vertically opposite angles are equal.The pairs of corresponding angles are equal.The pairs of alternate exterior angles are equal.The pairs of alternate interior angles are equal.Given:
<1 = 7y -20
<2 = 5x - 38
<3 = 90
exterior angle = 3x -4
Using alternate interior angle
5x - 38 = 3x-4
2x = 34
x=17
So, <2 = (5(17)-38))
<2 =47
Using angle sum property
90°+47°+(7y-20)=180°
7y-20=43°
y=9
Hence, the value of x is 17 and y is 9.
Learn more about parallel lines here:
https://brainly.com/question/16701300
#SPJ5
Let {
a
n
}
be a sequence and L
a real number such that lim
n
→
[infinity]
a
n
=
L
. Prove that {
a
n
}
is bounded.
Answers
To prove that the sequence {an} is bounded, we can utilize the fact that the limit of the sequence exists. Since the limit of {an} as n approaches infinity is L, we can conclude that there exists some positive integer N such that for all n greater than or equal to N, the terms of the sequence are arbitrarily close to L.
1. By considering the terms up to index N-1, we can find a maximum value M that is greater than or equal to all those terms. By choosing the larger of M and L, we can establish an upper bound for all terms of the sequence.
2. Let's assume that the limit of {an} as n approaches infinity is L. This means that for any given positive epsilon, there exists a positive integer N such that for all n greater than or equal to N, the absolute value of (an - L) is less than epsilon. In other words, the terms of the sequence {an} become arbitrarily close to L as n becomes larger.
3. Now, let's consider the terms of the sequence up to index N-1. Since there are only finitely many terms before index N, we can find the maximum value among those terms, denoted as M. We know that M is greater than or equal to all the terms before index N.
4. To establish an upper bound for the entire sequence {an}, we consider two cases: (1) M is greater than or equal to L, and (2) M is less than L. In case (1), we choose M as the upper bound for the entire sequence {an}. Since M is greater than or equal to all terms before index N, and for all n greater than or equal to N, the terms become arbitrarily close to L, M serves as an upper bound for the entire sequence.
5. In case (2), we choose L as the upper bound for the entire sequence {an}. Since L is the limit of the sequence, and for all n greater than or equal to N, the terms become arbitrarily close to L, L serves as an upper bound for the entire sequence.
6. Therefore, we have shown that in both cases, the sequence {an} is bounded, with an upper bound of either M or L, depending on the situation.
Learn more about sequence here: brainly.com/question/29394831
#SPJ11
If the scale factor between trapezoid ABCD and trapezoid is GHIJ is 2, how many feet will side GJ be?
Answers
Kindly find required figure in the picture attached below :
Answer:
14 feets
Step-by-step explanation:
From Trapezoid ABCD ;
The longer base, AD = 7 feets
Shorter Base ; BC = 5 feets
The Trapezoid GHIJ
Shorter Base = HI
Longer base = GJ
Given that the scale factor between ABCD and GHIJ is 2 ; then
GJ is similar to AD
Hence, side GJ = 2 * length of AD
GJ = 2 * 7 = 14 feets

need help on this one!!

Answers
Step-by-step explanation:
the square root of x squared is x.
this means the( cube root of x ) to the power of 6 is what we need
Solve the equation t − 5 = 12 for t.
17
7
−7
−17
Answers
Step-by-step explanation:
t - 5 = 12 | add 5 to both sides
t = 17
and that is it. that's all we needed to do.
Add 5 plus 12 and it equals 17 which you can sub in for y and it equals 12
At a coffee shop, two sizes of coffee are sold. A medium coffee costs $3, and a large coffee costs $5. Write an equation that represents the relationship between the number of medium coffees sold, x, and the number of large coffees sold, y, in an hour where sales totaled $68.
Answers
The equation that represent the relationship of the coffees is 3x + 5y = 68.
How to represent situation with system of equation?At a coffee shop, two sizes of coffee are sold. A medium coffee costs $3, and a large coffee costs $5.
The equation that represent the relationship between the number of medium coffees sold, x, and the number of large coffees sold, y, in an hour where sales totalled $68 is as follows:
where
x = number of medium coffees soldy = number of large coffees soldTherefore, the equation is as follows:
3x + 5y = 68
learn more on equation here:https://brainly.com/question/14177953
#SPJ1
f(−2) = ________ need help

Answers
Answer:
The answer is c
Step-by-step explanation:
Is the relation shown in the arrow diagram a function? Justify your answer.
Alternative text
Yes. The input 0.8 and 0.4 have only one output.
Yes. Each output has only one input.
No. Each input has only one output.
No. The input 1.2 has 2 outputs.
Answers
Answer:
No. The input 1.2 has 2 outputs.
Step-by-step explanation:
See attachment for complete question
The first circle represents the domain while the second represents the range of the function.
For a mapping to be a function, it must either be a one to one relationship or a many to one relationship.
One to one, in the sense that; there can be only one entry in the domain points to one entry in the range of the function.
Many to one, in the sense that: there can be multiple domain entries that point to one entry in the range of the function
However, from the attachment it can be seen that an entry in the domain (1.2) points to two entries in the range (6 and 8).
Hence, this does not represent a function.

Select the solutions of the equation.(select all that apply)
x2+4= 0
A.-2i
B.-2
C. 2i
D.2
Answers
This is because it is the sqrt(-4)
Can someone help me with stats?

Answers
Answer:
Step-by-step explanation:
I believe this is right.
Define T= X + Y
a. Find and Interpret Mu T.
Mu T= Mu x+y
Mu x+y= Mu x + Mu y
Mu x+y= 4.75+ 4.9
Mu T= 9.65
b. Calculate and Interpret Sigma T.
Sigma T= Sigma x+y
Sigma x+y= √σ^2 (of x)+ σ^2 (of y)
Sigma x+y= √(0.698)^2+(0.768)^2
Sigma T= 1.0378
Identify the correct graph of the system of equations. 3x − y = 12 x + 4y = 4 The graph shows a line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma 12. The graph shows a line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 12. The graph shows a line with an x--intercept at 4 comma 0 and a y-intercept at 0 comma negative 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma 12. The graph shows a line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 12.
Answers
The correct graph of the system of equations is D) The graph shows a line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 12.
What is the system of equations?
A system of equations is a set of two or more equations with the same variables. The goal of a system of equations is to find the values of the variables that simultaneously satisfy all the equations in the system.
The given equations are
3x + y = 12
x + 4y = 4
To graph the system of equations, we can start by finding the x-intercepts and y-intercepts of each line.
The x-intercept is the point where the line crosses the x-axis, which means that the y-value is 0. To find the x-intercept, we can set y = 0 and solve for x:
3x + y = 12
3x + 0 = 12
3x = 12
x = 4
So, the x-intercept of the first line is (4, 0).
Next, we can find the y-intercept, which is the point where the line crosses the y-axis, meaning that the x-value is 0. To find the y-intercept, we can set x = 0 and solve for y:
3x + y = 12
0 + y = 12
y = 12
So, the y-intercept of the first line is (0, 12).
We can repeat this process for the second line to find its x-intercept and y-intercept:
x + 4y = 4
x + 4 * 0 = 4
x = 4
So, the x-intercept of the second line is (4, 0).
Next, we can find the y-intercept by setting x = 0:
x + 4y = 4
0 + 4y = 4
4y = 4
y = 1
So, the y-intercept of the second line is (0, 1).
Now that we have found the x-intercepts and y-intercepts of each line, we can plot these points on a coordinate plane and draw lines through them to obtain the graph of the system of equations.
The graph shows a line with an x-intercept at (4, 0) and a y-intercept at (0, 12). There is a second line with an x-intercept at (4, 0) and a y-intercept at (0, 1).
Therefore, the correct graph of the system of equations is D) The graph shows a line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 1. There is a second line with an x-intercept at 4 comma 0 and a y-intercept at 0 comma negative 12.
To learn more about the system of equations, visit:
https://brainly.com/question/13729904
#SPJ1
LAST ONE PLS HELP PLS ASAP PLS PLS HELP ASAP THANKS ILL GIVE BRAINLKEST PLS THANKS PLS

Answers
Answer:
1/5
Step-by-step explanation:
Total Frequency is 14+21+70 = 105
Sewing has frequency of 21
21/105 = 0.2 = 1/5
Find 8 4 x sin(x2) dx 0 = 8 · 1 2 16 sin(u) du?
Answers
We can find the value of the integral ∫ 0 8 4 x sin(x^2) dx by using the substitution u = x^2 and evaluating the resulting integral ∫ 0 64 sin(u) du/2. The final answer is 4 - 4cos(64).
To solve this problem, we need to use a substitution. Let u = x^2, then du = 2x dx. We can rewrite the integral as:
∫ 0 8 4 x sin(x^2) dx = ∫ 0 64 sin(u) du/2
Using the limits of integration, we can evaluate the integral as follows:
∫ 0 64 sin(u) du/2 = [-cos(u)/2] from 0 to 64
= (-cos(64)/2) - (-cos(0)/2)
= (cos(0)/2) - (cos(64)/2)
= (1/2) - (cos(64)/2)
Therefore, the answer to the integral is:
∫ 0 8 4 x sin(x^2) dx = 8 · 1/2 - 8 · cos(64)/2
= 4 - 4cos(64)
Know more about integration here:
https://brainly.com/question/18125359
#SPJ11
The base of a hexagonal pyramid has an area of 82 square inches.The height of the pyramid is 9 inches.Find the volume of the pyramid.
Answers
The volume of the hexagonal pyramid is 246 inches squared.
How to find the volume of a pyramid?The base of a hexagonal pyramid has an area of 82 square inches. The height of the pyramid is 9 inches.
Therefore, the volume of the pyramid can be found as follows:
Volume of a pyramid = 1 / 3 Bh
where
B = base areah = height of the pyramidTherefore,
Volume of the pyramid = 1 / 3 × 82 × 9
Volume of the pyramid = 738 / 3
Volume of the pyramid = 246 inches³
learn more on pyramid here: https://brainly.com/question/31951661
#SPJ1
What are the perimeter and the area of a rectangle that is 3/4 yd long and a 1/3 yard wide
Answers
Answer:
Step-by-step explanation:
1/4 if you multiplying
1 1 /12 if you adding
Answer:
perimeter: \(2\frac{1}{6}\) yards
Area: \(\frac{1}{4}\) \(yards^{2}\)
Step-by-step explanation:
perimeter is 2(l)+2(w)
And area is (l)(w)
So to find perimeter we fill in the formula
2(3/4)+2(1/3)
6/4+2/3
Find common denominator
6*3/4*3+2*4/3*4
18/12+8/12
26/12
2 2/12
2 1/6 is the perimeter
Now for the area we multiply width by length
3/4x1/3
3/12
1/4 is the area
Hopes this helps please mark brainliest
Figure 222 is a scaled copy of Figure 111.
PLEASE HELP
Identify the side in Figure 222 that corresponds to side \overline{CD}
CD
start overline, C, D, end overline in Figure 111.
Choose 1 answer:
Choose 1 answer:
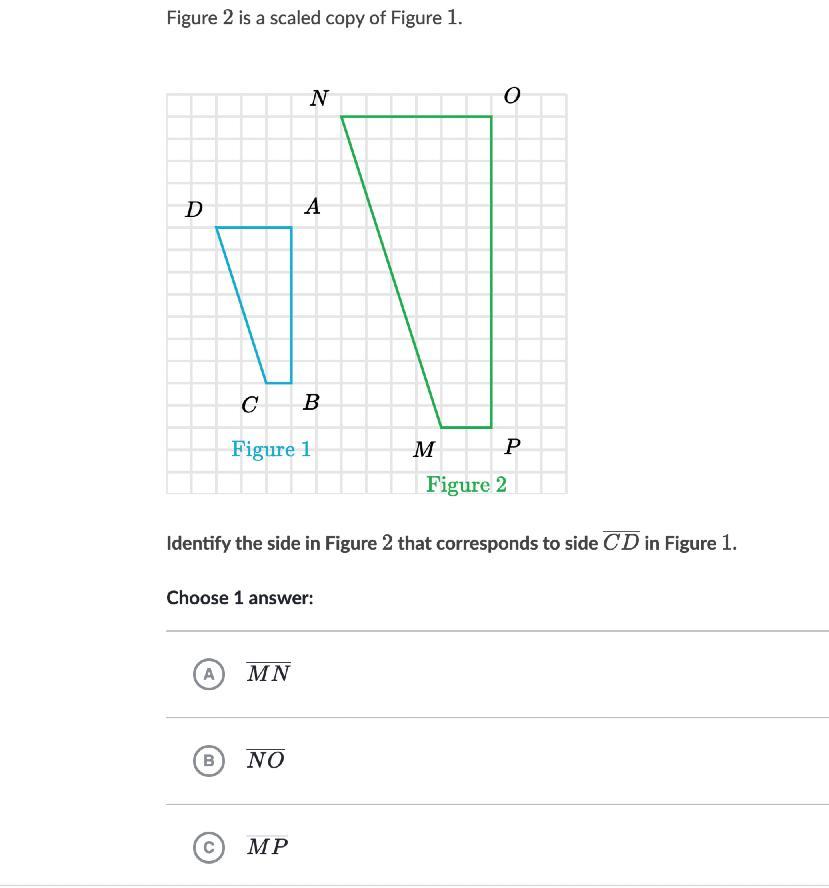
Answers
The bar graph in the following graphic represents fictional net exports in billions of dollars for five countries. Net exports are obtained by subtracting total imports from total exports; a negative net export means the country imported more goods than it exported.
What is the sum of net exports for Germany and China ?
a.
-80 billion dollars
c.
90 billion dollars
b.
180 billion dollars
d.
150 billion dollars

Answers
Answer:
d.) 150 billion dollars
Step-by-step explanation:
As per the given bar graph, we can draw the following conclusions:
Net exports for United States = ~ -110 Billion Dollars (It means import of 110 Billion Dollars)
Net exports for Denmark = ~ -30 Billion Dollars (It means import of 30 Billion Dollars)
Net exports for China = ~ 115 Billion Dollars
Net exports for Germany = ~ 35 Billion Dollars
We have to find the sum of net exports of Germany and China:
\(\Rightarrow\) 35 + 115 = 150 Billion Dollars.
Hence, correct answer is d. 150 Billion Dollars.
Answer: d
Step-by-step explanation:
150 billion dollars
Find the area of the surface. The part of the plane x+2y+3z=1 that lies inside the cylinder x2 + y2=3.
Answers
After calculating the partial derivatives and the cross product, we can find the double integral of the magnitude over the region (0 ≤ r ≤ √3, 0 ≤ θ ≤ 2π). This double integral gives the surface area of the part of the plane inside the cylinder.
To find the area of the surface of the part of the plane x + 2y + 3z = 1 that lies inside the cylinder x^2 + y^2 = 3, we can use a parametric representation for the plane and cylinder intersection.
Let x = r * cos(θ) and y = r * sin(θ), where r^2 = 3 (from the cylinder equation). Now, we can find z in terms of r and θ using the plane equation:
z = (1 - x - 2y) / 3
z = (1 - r * cos(θ) - 2r * sin(θ)) / 3
Now, we have the parametric representation of the intersection: (r * cos(θ), r * sin(θ), (1 - r * cos(θ) - 2r * sin(θ)) / 3). To find the surface area, we need to calculate the partial derivatives with respect to r and θ and then find the magnitude of the cross product.
After calculating the partial derivatives and the cross product, we can find the double integral of the magnitude over the region (0 ≤ r ≤ √3, 0 ≤ θ ≤ 2π). This double integral gives the surface area of the part of the plane inside the cylinder.
To know more about Derivatives visit :
https://brainly.com/question/29144258
#SPJ11
A local restaurant served 124 cups of pancake mix every hour it takes 1 1/4 cups of mix to make one pancake the pancakes are all equal in size about how many pancakes can the restaurant make in two hours
Answers
Answer: The restaurant can make 199 pancakes in two hours.
Step-by-step explanation:
Given: Total number of cups of pancake mix used in 1 hour = 124
Mix required for each pancake = \(1\dfrac14=\dfrac{5}{4}\)
Number of cups of pancake mix used in 2 hours = 2 x 124 = 248
Number of pancakes made = (Number of cups of pancake mix used in 2 hours ) ÷ (Mix required for each pancake )
\(=248\div\dfrac54\\\\=248\times\dfrac45\\\\= 198.4\approx199\)
Hence, the restaurant can make 199 pancakes in two hours.
A right triangle has side lengths that are consecutive interest and a perimeter of 12 feet what are the angles of the triangle
Answers
Answer:
Step-by-step explanation:
The sides are consecutive integers and the perimeter is 12 ft.
3 ft, 4 ft, 5 ft
One angle is 90°, one angle is arcsin(3/5) ≅ 36.9°
the remaining angle is 90-36.9 = 53.1°
if we compute a 95onfidence interval 12.65 ≤ μ ≤ 25.65 , then we can conclude that.
Answers
Based on the computed 95% confidence interval, we can conclude that we are 95% confident that the true population mean falls within the range of 12.65 to 25.65.
A confidence interval is a range of values that provides an estimate of the true population parameter. In this case, we are interested in estimating the population mean (μ). The 95% confidence interval, as mentioned, is given as 12.65 ≤ μ ≤ 25.65.
Interpreting this confidence interval, we can say that if we were to repeat the sampling process many times and construct 95% confidence intervals from each sample, approximately 95% of those intervals would contain the true population mean.
The confidence level chosen, 95%, represents the probability that the interval captures the true population mean. It is a measure of the confidence or certainty we have in the estimation. However, it does not guarantee that a specific interval from a particular sample contains the true population mean.
Therefore, based on the computed 95% confidence interval, we can conclude that we are 95% confident that the true population mean falls within the range of 12.65 to 25.65.
Learn more about confidence interval here:
https://brainly.com/question/13067956
#SPJ11
Solve the following equation: 3.3+4x=-6.9x+6.6
Round your answer to the nearest tenth.
Answers
The solution to the equation 3.3 + 4x = -6.9x + 6.6, rounded to the nearest tenth, is x ≈ 0.3.
To solve the equation 3.3 + 4x = -6.9x + 6.6, we need to isolate the variable x on one side of the equation.
First, let's simplify the equation by combining like terms:
3.3 + 4x = -6.9x + 6.6
Next, let's move the variable terms (4x and -6.9x) to one side and the constant terms (3.3 and 6.6) to the other side:
4x + 6.9x = 6.6 - 3.3
Combine the x terms on the left side:
10.9x = 3.3
Now, divide both sides of the equation by 10.9 to solve for x:
x = 3.3 / 10.9
Using a calculator, we can find the decimal approximation of x:
x ≈ 0.3028
Rounding to the nearest tenth, the solution to the equation is x ≈ 0.3.
In summary, the solution to the equation 3.3 + 4x = -6.9x + 6.6, rounded to the nearest tenth, is x ≈ 0.3.
To learn more about the equation;
https://brainly.com/question/12788590
#SPJ1
What is The answer to this problem -k+16-12k
Answers
Answer: The answer is − 1 3 + 1 6
I accidentally posted this without the picture but please answer

Answers
Answer:
i think its A sorry if wrong
Step-by-step explanation:
student masterconnect3. Which point is not a solution to the equation 2y + x = 87A (5, 1.5)B. (2, 3)C. (1, 4.5)D. (3, 2)

Answers
To determine if the point is a solution or not, we have to substitute the x-value and see if the y-value is correct:
*For x=5
\(\begin{gathered} -2y+5=8 \\ -2y=8-5 \\ y=-\frac{3}{2} \\ y=-1.5 \end{gathered}\)For x=2
\(\begin{gathered} -2y+2=8 \\ -2y=8-2 \\ y=-\frac{6}{2} \\ y=-3 \end{gathered}\)For x=-1
\(\begin{gathered} -2y-1=8 \\ -2y=8+1 \\ y=-\frac{9}{2} \\ y=-4.5 \end{gathered}\)For x=-3
\(\begin{gathered} -2y-3=8 \\ -2y=8+3 \\ y=\frac{11}{-2} \\ y=-5.5 \end{gathered}\)Then, the point that is NOT a solution for the equation is D. (-3, 2). The solution for x=-3 is -5.5.
The sum of 38 and twice a number x is 124. What is -2x - 5?
A)
-101
B)
-91
C)
46
D)
86
Answers
Answer:
B). - 91
Explanation:
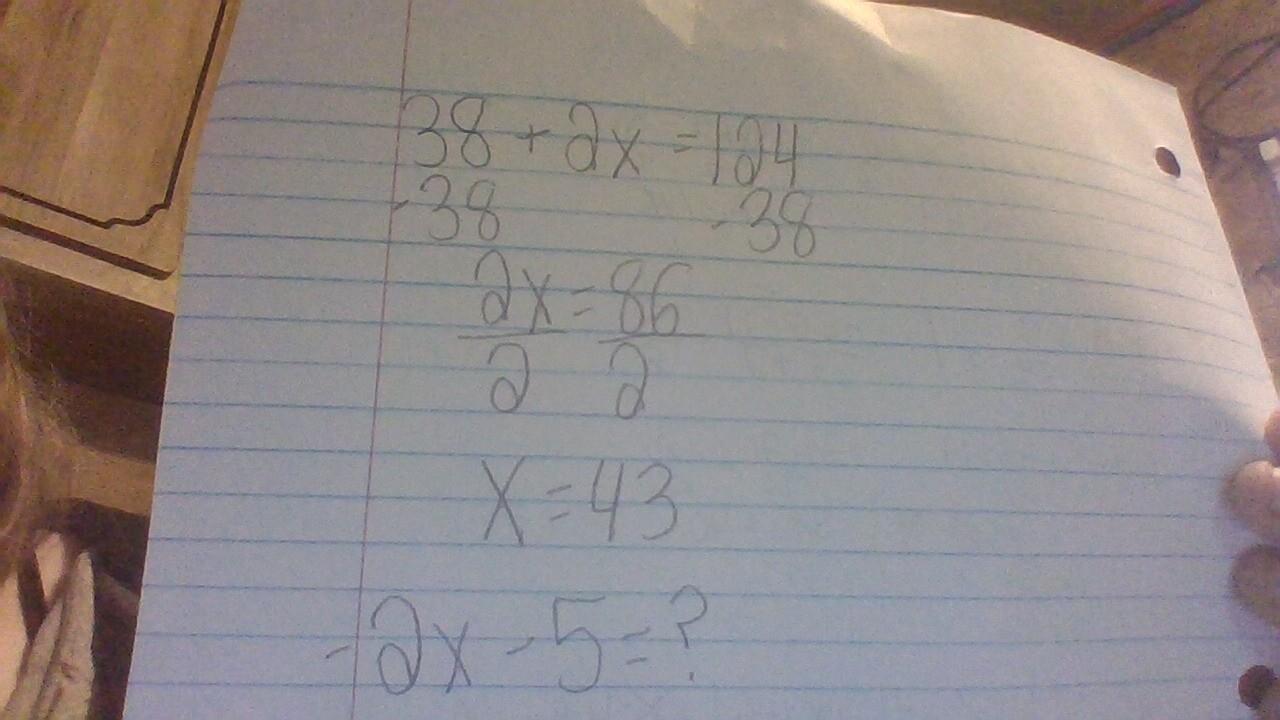

8x +32
Factor the gcf
Answers
Answer:
8(x+4)
Step-by-step explanation:
8x+32
nope that helped
Find the general solution to the given system. X' = (12 -9)X
(4 0)
Answers
The general solution to the given initial value problem is:
\(x_1(t) = 3c_1 * e^{6t},\\x_2(t) = 2c_1 * e^{6t}.\)
To find the general solution to the given system:
\(X' = \left[\begin{array}{ccc}12&-9\\4&0\end{array}\right]\)
Let X = [\(x_1; x_2\)] be the vector of variables, and X' represents its derivative.
The system of equations can be written as:
\(x_1' = 12x_1 - 9x_2\\x_2' = 4x_1 + 0x_2\)
To solve this system, we can rewrite it in matrix form:
X' = AX,
where A is the coefficient matrix:
\(A = \left[\begin{array}{ccc}12&-9\\4&0\end{array}\right]\)
To find the general solution, we need to find the eigenvalues and eigenvectors of matrix A.
First, we find the eigenvalues by solving the characteristic equation:
|A - λI| = 0,
where λ is the eigenvalue and I is the identity matrix.
A - λI = \(\left[\begin{array}{ccc}12-\lambda&-9\\4&-\lambda\end{array}\right]\)
Setting the determinant equal to zero:
(12 - λ)(-λ) - (-9)(4) = 0,
-λ(12 - λ) + 36 = 0,
\(\lambda^2 - 12\lambda + 36 = 0.\)
Factoring the quadratic equation:
(λ - 6)(λ - 6) = 0,
λ = 6.
Since we have repeated eigenvalue (λ = 6), we need to find the corresponding eigenvectors.
For λ = 6, we solve the equation (A - 6I)V = 0, where V is the eigenvector.
(A - 6I)V = [12 - 6 -9]\([v_1]\) = 0,
[4 -6] [\(v_2\)]
\(6v_1 - 9v_2 = 0,\\4v_1 - 6v_2 = 0.\)
We can choose \(v_1\) = 3 as a free variable.
Using \(v_1\) = 3, we get:
\(6(3) - 9v_2 = 0,\\4(3) - 6v_2 = 0.18 - 9v_2 = 0,\\12 - 6v_2 = 0.-9v_2 = -18,\\-6v_2 = -12.v_2 = 2.\)
Thus, the eigenvector corresponding to λ = 6 is V = [3; 2].
The general solution to the system is given by:
\(X(t) = c_1 * e^{6t} * V,\)
where c1 is an arbitrary constant and V is the eigenvector.
Substituting the values, we have:
\(X(t) = c_1 * e^{6t}\) * [3; 2],
or
\(x_1(t) = 3c_1 * e^{6t},\\x_2(t) = 2c_1 * e^{6t}.\)
Therefore, the general solution to the given system is:
\(x_1(t) = 3c_1 * e^{6t},\\x_2(t) = 2c_1 * e^{6t}.\)
To learn more about the initial value problem visit,
brainly.com/question/29594052
#SPJ4
Paul brought $24.50 to the art supply store. He bought a brush, a sketchbook, and a paint set. The brush was 1 3 as much as the sketchbook, and the sketchbook cost 1 2 the cost of the paint set. Paul had $2.00 left over after buying these items. What was the cost of each item
Answers
Answer:
so do
24.50-13=11.50
11.50-12.00= answer
Step-by-step explanation:
I think so
You are choosing between two health clubs. club a offers a membership for a fee of $40
Answers
After 5 months the total cost at each health club be the same.
Given that, club A offers membership for a fee of $40 plus a monthly fee of $25.
Let the number of months be x.
Membership fee of club A = 40+25x ------(i)
Club B offers a membership fee of $15 plus a monthly fee of $30.
Membership fee of club B = 15+30x
The total cost at each health club be the same
40+25x = 15+30x
30x-25x=40-15
5x=25
x=25/5
x=5
Therefore, after 5 months the total cost at each health club be the same.
To learn more about an equation visit:
https://brainly.com/question/14686792.
#SPJ4
"Your question is incomplete, probably the complete question/missing part is:"
You are choosing between two health clubs. Club A offers membership for a fee of $40 plus a monthly fee of $25. Club B offers a membership fee of $15 plus a monthly fee of $30.
Using variables of your choice, set-up an equation for each club’s membership cost. Make sure your variables are defined clearly.
After how many months will the total cost at each health club be the same?