The number of revolutions
made by a tire traveling over a fixed distance
varies inversely with the radius of the tire. a
12-inch radius tire makes 100 revolutions to
travel a certain distance. how many
revolutions would a 16-inch radius tire require
a
to travel the same distance?
define variables
identify constant of variation
write an equation and show work (please can someone help with this stuff, my deadline is in 4 days)
Answers
A 16-inch radius tire would require 75 revolutions to travel the same distance as a 12-inch radius tire that made 100 revolutions.
Let's start by defining some variables. Let "r" represent the radius of the tire and "n" represent the number of revolutions it makes over a fixed distance. We are given that the number of revolutions is inversely proportional to the radius of the tire. This means that as the radius increases, the number of revolutions decreases, and vice versa. We can express this relationship mathematically as follows:
n = k/r
Here, "k" is the constant of variation, which remains the same for any given tire traveling over the same distance. To solve the problem, we need to find the value of "k" first. We know that a 12-inch radius tire makes 100 revolutions to travel a certain distance. Substituting these values into the equation, we get:
100 = k/12
Solving for "k," we get k = 1200. Now we can use this value to find the number of revolutions required by a 16-inch radius tire to travel the same distance:
n = 1200/16 = 75
Therefore, a 16-inch radius tire would require 75 revolutions to travel the same distance as a 12-inch radius tire that made 100 revolutions.
In summary, we defined the variables, identified the constant of variation, wrote the equation (n=k/r), found the value of the constant by using the given information, and used it to solve the problem by finding the number of revolutions required by a tire with a different radius.
Know more about revolutions here:
https://brainly.com/question/20700248
#SPJ11
Related Questions
How do you calculate chain rule?
Answers
Answer:
If y = f(g(x)), then as per chain rule the instantaneous rate of change of function 'f' relative to 'g' and 'g' relative to x results in an instantaneous rate of change of 'f' with respect to 'x'. Hence, the derivative of y will be given as, y' = f'(g(x)).
Step-by-step explanation:
If y = f(g(x)), then as per chain rule the instantaneous rate of change of function 'f' relative to 'g' and 'g' relative to x results in an instantaneous rate of change of 'f' with respect to 'x'. Hence, the derivative of y will be given as, y' = f'(g(x)).
1. A variable is normally distributed with a mean of 16 and a standard deviation of 6 . Find the percent of the data set that: (a) is greater than 16 (b) falls between 10 and 22 (c) is greater than 28 (d) is less than 1 (e) falls between 4 and 19 (f) falls between 22 and 31 APPLICATIONS 2. The weights of Siamese cats are normally distributed with a mean of 6.4 pounds and a standard deviation of 0.8 pounds. If a breeder of Siamese cats has 128 in his care, how many can he expect to have weights between 5.2 and 7.6 pounds? (1) 106 (3) 98 (2) 49 (4) 111 3. If one quart bottles of apple juice have weights that are normally distributed with a mean of 64 ounces and a standard deviation of 3 ounces, what percent of bottles would be expected to have less than 58 ounces? (1) 6.7% (3) 0.6% (2) 15.0% (4) 2.3% 4. Historically daily high temperatures in July in Red Hook, New York, are normally distributed with a mean of 84
∘
F and a standard deviation of 4
∘
F. How many of the 31 days of July can a person expect to have temperatures above 90
∘
F ?
Answers
1. (a) 50% of the data set is greater than 16.
(b) 68.26% of the data set falls between 10 and 22.
(c) 2.28% of the data set is greater than 28.
(d) 0.62% of the data set is less than 1.
(e) 66.87% of the data set falls between 4 and 19.
(f) 15.25% of the data set falls between 22 and 31.
2. the breeder can expect to have approximately 111 Siamese cats with weights between 5.2 and 7.6 pounds.
3. approximately 2.28% of the bottles would be expected to have less than 58 ounces.
(a) Since the variable is normally distributed with a mean of 16 and a standard deviation of 6, we can use the Z-score formula:
Z = (X - μ) / σ
where X is the value we're interested in, μ is the mean, and σ is the standard deviation.
X = 16, μ = 16, and σ = 6.
Z = (16 - 16) / 6 = 0
The Z-score of 0 corresponds to the mean of the distribution. To find the area to the right of 16, we can look up the Z-score of 0 in the standard normal distribution table, which gives us a value of 0.5000. However, since we want the area to the right, we subtract this value from 1:
1 - 0.5000 = 0.5000
Therefore, 50% of the data set is greater than 16.
(b) To find the percent of the data set that falls between 10 and 22, we can calculate the area under the normal distribution curve between these two values.
Z₁ = (10 - 16) / 6 = -1.00
Z₂ = (22 - 16) / 6 = 1.00
Looking up these Z-scores in the standard normal distribution table, we find that the area to the left of Z = -1.00 is 0.1587 and the area to the left of Z = 1.00 is 0.8413. To find the area between these two Z-scores, we subtract the smaller area from the larger area:
0.8413 - 0.1587 = 0.6826
Therefore, 68.26% of the data set falls between 10 and 22.
(c) To find the percent of the data set that is greater than 28
Z = (28 - 16) / 6 = 2.00
Looking up this Z-score in the standard normal distribution table, we find that the area to the left of Z = 2.00 is 0.9772. Since we want the area to the right, we subtract this value from 1:
1 - 0.9772 = 0.0228
Therefore, 2.28% of the data set is greater than 28.
(d) To find the percent of the data set that is less than 1
Z = (1 - 16) / 6 = -2.50
Looking up this Z-score in the standard normal distribution table, we find that the area to the left of Z = -2.50 is 0.0062. Therefore, 0.62% of the data set is less than 1.
(e) To find the percent of the data set that falls between 4 and 19
Z₁ = (4 - 16) / 6 = -2.00
Z₂ = (19 - 16) / 6 = 0.50
Looking up these Z-scores in the standard normal distribution table, we find that the area to the left of Z = -2.00 is 0.0228 and the area to the left of Z = 0.50 is 0.6915. Subtracting the smaller area from the larger area:
0.6915 - 0.0228 = 0.6687
Therefore, 66.87% of the data set falls between 4 and 19.
(f) To find the percent of the data set that falls between 22 and 31
Z₁ = (22 - 16) / 6 = 1.00
Z₂ = (31 - 16) / 6 = 2.50
Looking up these Z-scores in the standard normal distribution table, we find that the area to the left of Z = 1.00 is 0.8413 and the area to the left of Z = 2.50 is 0.9938. Subtracting the smaller area from the larger area:
0.9938 - 0.8413 = 0.1525
Therefore, 15.25% of the data set falls between 22 and 31.
2. For the weights of Siamese cats, which are normally distributed with a mean of 6.4 pounds and a standard deviation of 0.8 pounds, we want to find the number of cats that have weights between 5.2 and 7.6 pounds.
Z₁ = (5.2 - 6.4) / 0.8 = -1.5
Z₂ = (7.6 - 6.4) / 0.8 = 1.5
The area to the left of Z = -1.5 is 0.0668, and the area to the left of Z = 1.5 is 0.9332. To find the area between these two Z-scores, we subtract the smaller area from the larger area:
0.9332 - 0.0668 = 0.8664
This means that 86.64% of Siamese cats are expected to have weights between 5.2 and 7.6 pounds.
To find the number of cats in a sample of 128 cats, we can multiply the percent by the total number of cats:
0.8664 * 128 = 110.87
Rounding to the nearest whole number, the breeder can expect to have approximately 111 Siamese cats with weights between 5.2 and 7.6 pounds.
3. For one quart bottles of apple juice with weights normally distributed with a mean of 64 ounces and a standard deviation of 3 ounces, we want to find the percent of bottles that would be expected to have less than 58 ounces.
To calculate this, we can convert the weight of 58 ounces to a Z-score:
Z = (58 - 64) / 3 = -2
Looking up the Z-score of -2 in the standard normal distribution table, we find that the area to the left of Z = -2 is 0.0228. Therefore, approximately 2.28% of the bottles would be expected to have less than 58 ounces.
Learn more about Z-score here
https://brainly.com/question/31871890
#SPJ4
In ΔOPQ, \text{m}\angle O = (2x-5)^{\circ}m∠O=(2x−5) ∘
, \text{m}\angle P = (3x-8)^{\circ}m∠P=(3x−8) ∘
, and \text{m}\angle Q = (10x-17)^{\circ}m∠Q=(10x−17) ∘. What is the value of x?x?
Answers
Answer: 14
Step-by-step explanation:
Expand (x-4)^4 with binomial theorem or pascal's triangle SHOW ALL STEPS!
PLS HELP ASAP WILL GIVE BRAINLIEST TO WHOEVER SHOWS ALL STEPS!
Answers
Answer:
x^4 - 16x^3 + 96x^2 -256x + 256
Step-by-step explanation:
The coefficients of this using the pascal triangle is ;
1 4 6 4 1
Thus, we have that;
1(x^4•(-4)^0) + 4(x^3)(-4)^1 + 6(x^2)(-4^2) + 4(x^1)(-4)^3 + 1(x^0)(-4)^4
= x^4 - 16x^3 + 96x^2 -256x + 256
2) If a system of linear equations has one solution, what does this mean
about the two lines?
A. intersecting lines
B. same lines
C. parallel lines
D. skew lines
Answers
Answer:
A is the answer half Irish die f Russian stuff right stuff he taught
Step-by-step explanation:
10/94+641=68000
the biblical account of joshua's long day is a miracle of: timing intervention of natural laws visible appearance all of these
Answers
Answer:
According to search result [1], the Biblical account of Joshua's long day is a miracle of "all of these": timing, intervention of natural laws, and visible appearance.
Step-by-step explanation:
Jeremy and Robin like to collect nickels. Jeremy has n nickels,
and Robin has 55 nickels. Together they have a total of 100
nickels.
Write an equation to describe this situation.
Report a problem
Answers
Answer:
n+55=100
Step-by-step explanation:
What is the equation of the graphed line written in standard form?
2x + 3y = -6
2x + 3y = 6
y=-2/3x-2
y= 2/3x-2
Answers
Answer:
What is the equation of the graphed line written in standard form?" has four options: 2x + 3y = -6, 2x + 3y = 6, y=-2/3x-2, and y= 2/3x-2. The standard form of a linear equation is Ax + By = C, where A, B, and C are constants. In this case, the first two options, 2x + 3y = -6 and 2x + 3y = 6 are already in standard form. The last two options, y=-2/3x-2 and y= 2/3x-2 are not in standard form. However, without additional information such as a graph or coordinates of points on the line, it is not possible to determine which of these options is the correct equation for the graphed line.
MARK AS BRAINLIEST!!!
Consider a committee consists of three members Rita, Sid and Tina. The Committee purports to decide between TWO options each time. The committee decision is determined by majority voting. There are four options A,B,C and D in total. We define the committee's preference Com based on the voting outcome: Suppose two options X and Y are put to vote. If committee always selects X, then X Com Y. If committee sometimes chooses X and sometimes chooses Y, then X Com Y Every committee member's preference is rational. They sincerely vote for their own preferred option (a) Suppose the committee members' preferences are given by • Rita's preference is ABD >C. • Sid's preference is B>D>A> C. Tina's preference is C > B>A> D. Write down a utility function representing the committee's preference. That is, what are the utility levels assigned to the options? (b) Suppose Rita leaves the committee and is succeeded by Ray. Ray's preference is A>D>> B. The committee's decision will be different. Find out the new committee's preference, and explain whether the new committee's preference can be represented by a utility function. Hint: The committee's preference needs not be rational. In this case, you should first work out the committee's preference for every pair of options.
Answers
The committee's preference is determined by majority voting. Each committee member has their own preference ranking for the options. Using the given preferences of Rita, Sid, and Tina, we can derive a utility function representing the committee's preference. However, when Rita is replaced by Ray, the new committee's preference may not be representable by a utility function.
To represent the committee's preference with a utility function, we assign utility levels to the options based on the given preferences. Let's denote the options as A, B, C, and D. From Rita's preference (ABD > C), we can assign a higher utility to options A, B, and D compared to option C. Sid's preference (B > D > A > C) implies that B has the highest utility, followed by D, A, and then C. Tina's preference (C > B > A > D) suggests that C has the highest utility, followed by B, A, and then D. Combining these preferences, we can assign utility levels to the options: U(A) > U(B) > U(C) > U(D).
When Rita is replaced by Ray, Ray's preference (A > D >> B) introduces a change in the committee's decision. To determine the new committee's preference, we need to consider all possible pairs of options and determine the majority preference in each case. For example, for the pair (A, B), Sid prefers B, Tina prefers A, and Ray prefers A. Thus, the majority preference is A > B. Similarly, we can analyze the preferences for other pairs and determine the committee's preference. However, it is important to note that the new committee's preference may not be representable by a utility function since it might not satisfy rationality properties such as transitivity or completeness. Utility functions are typically used to represent rational preferences, and in this case, the committee's preference might not adhere to rationality assumptions.
Learn more about utility function here:
https://brainly.com/question/32733866
#SPJ11
Find the result of |x-1|=2
Answers
The absolute value of x minus one is equal to two. Therefore, x must be either one greater than two (x = 3) or one less than two (x = 1).
One less than x results in a value of two in absolute terms. As a result, x minus 1 has an absolute value of 2, which is a positive number. The separation of an integer from zero is its absolute value. As a result, x minus 1 is two units from zero in absolute terms. As x minus one has an absolute value of two, its real value must either be two or a negative two. That is to say, x must either be one more than two (x = 3) or one less than two (x = 1).In order to confirm this, let's look at a few examples. If x = 3, then |x - 1| = |2 - 1| = |1| = 1 which is not equal to two. Therefore, x = 3 is not the answer we are looking for. On the other hand, if x = 1, then |x - 1| = |1 - 1| = |0| = 0 which is not equal to two. Therefore, x = 1 is also not the answer we are looking for. The only two possible solutions for the equation |x - 1| = 2 are x = 3 and x = 1. Therefore, the result of |x - 1| = 2 is that x must be either one greater than two (x = 3) or one less than two (x = 1)
Learn more about absolute value here
https://brainly.com/question/1301718
#SPJ4
If you borrow 700$ for five years at a annual interest rate of 7%, how much will you pay all together
Answers
Answer:
$2,245.
Step-by-step explanation:
Your interest will have grown to $2,245 dollars and you will have earned $1,545.
Hope this helped
HELLLLLLLLPPPPPPPPPPPP,
Find the value of x so that the function has the given value.
q(x)=12x−3; q(x)=−4
Answers
Answer:
-1/12
Step-by-step explanation:
12x-3 = -4
12x= -1
x= -1/12
help me out please explain too please :((
Answers
Answer:
bro I can’t do it TvT
how do you do problems like 4x=36 and -x=35
Answers
You have to divide both sides by the number that's multiplying x. A general example is:
\(ax=b\)To solve we have to divide both sides by a:
\(\begin{gathered} \frac{ax}{a}=\frac{b}{a} \\ x=\frac{b}{a} \end{gathered}\)find the value of w, need help quick pleaseeee
Answers
Answer:
w = 3
Step-by-step explanation:
we can solve with a proportion between the sides and the segments of the sides
9 ÷ 15 = w ÷ 5
w = 9 × 5 ÷ 15
w = 45 ÷ 15
w = 3
-------------------------
check9 ÷ 15 = 3 ÷ 5
0.6 = 0.6
same value the answer is good
how many meters are in 2.5 kilometers?
Answers
Answer:2500
Step-by-step explanation:
no cap
Answer:
2500 meters
Step-by-step explanation:
WILL MARK YOU BRAINLIEST HURRY IM ON A TIME LIMIT PLZ
Answers
Answer: L
Step-by-step explanation:
see in the picture, L is belong to the perpendicular bisector of RS
=> LR = LS (1)
L is belong to the perpendicular bisector of ST
=> LS = LT (2)
from (1)(2) => LS = LT = LR
=> L is equidistant from the points R, S, T
=> L is the center of circle
In Spring 2017, data was collected from a random selection of STA 2023 students. One of the questions asked how many hours they had exercised in the past 24 hours.For the 39 randomly selected upperclassmen, the sample mean was 0.76 and sample standard deviation was 0.75.For the 35 randomly selected underclassmen, the sample mean was 0.60 and the sample standard deviation was 0.73.What is the point estimate of the difference in the population mean exercised between underclassmen and upperclassmen?
Answers
The point estimate of the difference in the population mean exercised between underclassmen and upperclassmen is 0.16 hours.
In this case, we are estimating the difference in population means between two groups - upperclassmen and underclassmen. The point estimate is calculated by subtracting the sample mean of the underclassmen from the sample mean of the upperclassmen, which gives us
0.76 - 0.60 = 0.16.
the point estimate of the difference in population mean exercised between underclassmen and upperclassmen is 0.16 hours, which was calculated by subtracting the sample mean of underclassmen from the sample mean of upperclassmen.
Point Estimate = (Sample Mean of Upperclassmen) - (Sample Mean of Underclassmen)
Point Estimate = (0.76) - (0.60)
Point Estimate = 0.16
Hence, the point estimate of 0.16 suggests that, on average, upperclassmen exercised 0.16 hours more than underclassmen in the past 24 hours. This is a rough estimate of the difference between the two population means based on the provided sample data.
learn more about mean click here:
https://brainly.com/question/1136789
#SPJ11
BizCafe Simulation: Approximately how many medium cups of coffee will 30 lb. of coffee beans make?
Answers
Dividing the total ounces of brewed coffee by the size of a medium cup (8 ounces), we can estimate the number of medium cups of coffee:
8,160 ounces (brewed coffee) / 8 ounces (medium cup size) ≈ 1,020 medium cups of coffee.
To determine approximately how many medium cups of coffee 30 lb. of coffee beans will make, we need additional information about the brewing process, the coffee-to-water ratio, and the size of a medium cup of coffee in ounces or milliliters. Without these specific details, it is difficult to provide an accurate estimate.
However, as a general guideline, the coffee-to-water ratio typically used for brewing coffee is around 1:15 to 1:18. This means that for every gram or ounce of coffee, you would use 15 to 18 times the amount of water. Assuming a coffee-to-water ratio of 1:17, we can make an estimate.
Let's assume that a medium cup of coffee is approximately 8 ounces (236.6 milliliters). With a coffee-to-water ratio of 1:17, we would use 1 part coffee to 17 parts water. So, for every ounce of coffee beans, we would need approximately 17 ounces of water.
Now, converting the 30 lb. of coffee beans to ounces (1 lb. = 16 ounces), we have:
30 lb. * 16 ounces/lb. = 480 ounces of coffee beans.
Considering the coffee-to-water ratio and assuming 17 ounces of water for every ounce of coffee beans, we can estimate the total amount of brewed coffee:
480 ounces (coffee beans) * 17 (coffee-to-water ratio) = 8,160 ounces of brewed coffee.
Finally, dividing the total ounces of brewed coffee by the size of a medium cup (8 ounces), we can estimate the number of medium cups of coffee:
8,160 ounces (brewed coffee) / 8 ounces (medium cup size) ≈ 1,020 medium cups of coffee.
Please note that this is a rough estimate and can vary based on specific factors such as brewing method, coffee strength preferences, and cup sizes.
Learn more about number from
https://brainly.com/question/27894163
#SPJ11
PLEASE HELP NO LINKS OR FILES
1. When the outcome of one even has NO effect on the outcome of the other is called... A. likely events
B. dependent events
C. independent events
2.Lucy picks a marble at random. Without putting the first marble back, Lucy picks another marble at random. This is called...
A. independent probability
B. random ratios
C. dependent probability
D. natural occurrence
3. A bag contains 9 green marbles and 12 pink marbles. One marble is chosen at random and returned to the bag. Then, a second marble is chosen at random.
What is the probability that both marbles chosen will be green?
A. 6/9
B. 9/49
C. 3/4
D. 81/122
Answers
Answer:
1c
2c
3b
Step-by-step explanation:
What can divided 36 and 99
Answers
Step-by-step explanation:
GCF of 36 and 99 is the largest possible number that divides 36 and 99 exactly without any remainder. The factors of 36 and 99 are 1, 2, 3, 4, 6, 9, 12, 18, 36 and 1, 3, 9, 11, 33, 99 respectively.
I was going to just say the answer was 3 but the other person put multiple answers.So they have the correct answer.Good job!
Triangle ABC has vertices A(4, 4), B(1, 0), and C(1, 2). Find the coordinates vertex A after the triangle is dilated using a scale factor of 3. 5
Answers
Triangle ABC has vertices A(4, 4), B(1, 0), and C(1, 2). The coordinates of the vertex A' after the triangle is dilated using a scale factor of 3.5 is (14, 14).
Given the triangle ABC with vertices A(4, 4), B(1, 0), and C(1, 2).
Let A' be the vertex of triangle ABC after the dilation using a scale factor of 3.5
We know that the scale factor of dilation, say k, is equal to 3.5.
If (x, y) are the coordinates of vertex A', then coordinates of vertex A are (4, 4).
Then, using the scale factor k, we get:
x = k × 4
= 3.5 × 4
= 14y
= k × 4
= 3.5 × 4
= 14
Therefore, the coordinates of the vertex A' after the triangle is dilated using a scale factor of 3.5 is (14, 14).
Since the coordinates of vertex B and vertex C of the triangle ABC are already lying on the x-axis and y-axis respectively, their coordinates will remain the same after dilation.
Learn more about scale factor from the given link
https://brainly.com/question/25722260
#SPJ11
Given g(x)=4-2(3-x), what is the value of g(1)
Answers
Answer:
g(1) = 0
Step-by-step explanation:
To evaluate g(1) , substitute x = 1 into g(x), that is
g(1) = 4 - 2(3 - 1)
= 4 - 2(2)
= 4 - 4
= 0
Answer: its 0
Step-by-step explanation:
3. Solve the problem.In one area, the lowest angle of elevation of the sun in winter is 24°. Find the distance x that a plant needing full sun can be placed from a fence that is 10.5 feet high. Round your answer to the tenthsplace when necessary.
Answers
Answer:
The breakdown of the image of the question is given below as
Concept:
To figure out the value of x, we will use the trigonometric ratio below
\(\begin{gathered} \tan\theta=\frac{opposite}{adjacent} \\ opposite=10.5ft \\ adjacent=x \\ \theta=24^0 \end{gathered}\)By substituting the values, we will have
\(\begin{gathered} \tan\theta=\frac{oppos\imaginaryI te}{adjacent} \\ \tan24^0=\frac{10.5ft}{x} \\ \end{gathered}\)By cross multiplying the equation above, we will have
\(\begin{gathered} \tan24^0=\frac{10.5ft}{x} \\ x\times\tan24^0=10.5ft \\ divide\text{ both sides by tan24} \\ \frac{x\times\tan24^0}{tan24^0}=\frac{10.5ft}{\tan24^0} \\ x=23.58ft \\ x\approx23.6ft(nearest\text{ tenth\rparen} \end{gathered}\)Hence,
The final answer is
\(\Rightarrow x=23.6ft\)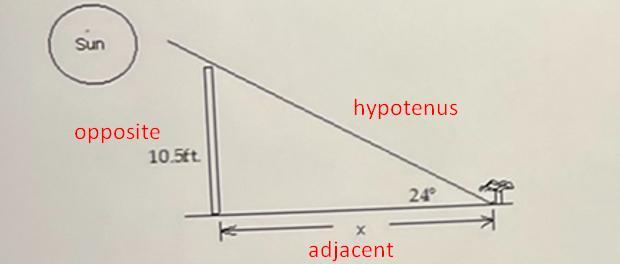
Which of the following is a trinomial with a constant term?
A. x - y + 3
B. y + x ^ 3
C. x ^ 7
D. x ^ 3 + 12x ^ 2 + x
E. x + 7y
F.y ^ 2 + 12
Answers
Answer:
A) x - y + 3
Step-by-step explanation:
A trinomial is a polynomial with 3 terms, and a constant term always stays constant (for example an integer). A seems to work best.
For the shape below, if side BD = 29 and side AC = 3x - 4, find x.
Answers
since sides BD and AC are congruent, then the equation would be 29=3x-4
Answer:
x = 11
Step-by-step explanation:
We know that the answer we will get will be the same as BD because BD and AC are congrudent, meaning that they are exactly equal shape and size. To find 'x' our equation would be: 29 = 3x - 4. To figure this out we just add 29 and 4 which gives us 33 and then divide that by 3 which gives us 11 (our answer)
Ben scored 3 times than Sam, together their score was 80. Find their scores.
Answers
Answer:
Sam = 20
Ben = 60
Step-by-step explanation:
We need to turn this into an equation.
Seeing as Ben is 3 times as much as Sam, if Sams score is represented by x then Ben can be 3* x or 3x, meaning:
3x + x = 80
4x = 80
Divide both sides by 4:
\(\frac{4x}{4} = \frac{80}{4}\)
x = 20
So Sam scored 20 and Ben scored 3 * 20 = 60.
Hope this helps!
Piper has a points card for a movie theater.
. She receives 60 rewards points just for signing up.
• She earns 13.5 points for each visit to the movie theater.
• She needs at least 195 points for a free movie ticket.
Write and solve an inequality which can be used to determine x, the number of visits
Piper can make to earn her first free movie ticket.
≤ ≥
Inequality:
Please send help
Answers
In order for there to be 10 visits, she needs to make 10.
What is system of linear equations?
The intersections or meetings of the lines or planes that represent the linear equations are known as the solutions of linear equations. The set of values for the variables in every feasible solution is known as a solution set for a system of linear equations.
points that piper earned 13.5x + 60
she cannot get free tickets until she has at least 195 points.
so 13.5x + 60 ≥ 195
13.5x ≥ 195 - 60
13.5x ≥ 135 x ≥ 10
So, In order for there to be 10 visits, she needs to make 10.
Learn more about the system of linear equations, by the following link.
https://brainly.com/question/25858757
#SPJ1
9. Look at some of the printed letters in a textbook. The small horizontal
and vertical segments attached to the ends of the letters are called
serifs. Most of the letters in a textbook are in a serif typeface. The
letters on this page do not have serifs, so these letters are in a sans-
serif typeface. (Sans means "without" in French.) The figure shows a
capital letter A with serifs. Use the given information to write a
paragraph proof that the serif, segment HI, is parallel to segment JK.
Given: 21 and 23 are supplementary.
Prove: HI || JK
Answers
By considering the given information that angles 21 and 23 are supplementary and analyzing the properties of supplementary angles and parallel lines, we have proven that segment HI is parallel to segment JK.
To prove that segment HI is parallel to segment JK based on the given information that angles 21 and 23 are supplementary, we can utilize the properties of supplementary angles and parallel lines.
First, let's examine the given figure and information.
We have a capital letter A with serifs, where segment HI represents one of the serifs, and segment JK represents a horizontal line within the letter A.
To begin the proof, we'll make use of the fact that angles 21 and 23 are supplementary.
Supplementary angles are defined as two angles whose measures sum up to 180 degrees.
We can observe that angle 21 is an interior angle of triangle AHI, and angle 23 is an interior angle of triangle AJK.
Since angles 21 and 23 are supplementary, their sum is equal to 180 degrees.
Now, let's assume that segments HI and JK are not parallel.
In this case, if we extend lines HA and JA, they will eventually intersect at point P.
Since the angles formed at the point of intersection are supplementary (angle 21 + angle 23 = 180 degrees), it would imply that angle 21 and angle PJK, as well as angle 23 and angle PHI, are also supplementary.
However, this leads to a contradiction. In the original figure, we can observe that angle 21 and angle PJK do not form a supplementary pair since angle PJK is a right angle (90 degrees) in the letter A.
Therefore, our assumption that segments HI and JK are not parallel must be incorrect.
Consequently, we can conclude that segment HI is indeed parallel to segment JK.
For similar question on angles.
https://brainly.com/question/25770607
#SPJ8
Solve the equation.
p−3=−4
p=
Answers
The value of p in the given equation is -1.
Given is an equation p-3 = -4, we need to find the value of p,
So,
p-3 = -4
p = -4+3
p = -1
Hence, the value of p in the given equation is -1.
Learn more about equations, click;
https://brainly.com/question/29657983
#SPJ1