The equation m = 1. 4p represents the mass, m, in grams, of
p polished stones.
Answers
We know that the total mass of 5 polished stones would be 7 grams according to this equation
Sure! The equation m = 1.4p represents the mass, m, in grams, of p polished stones.
This means that if you know the number of polished stones, p, you can use this equation to calculate their total mass, m, in grams. For example, if you have 5 polished stones, you can plug in p = 5 and solve for m: m = 1.4 x 5 = 7 grams.
So the total mass of 5 polished stones would be 7 grams according to this equation.
To know more about mass refer here
https://brainly.com/question/19694949#
#SPJ11
Based on the equation, the number of grams which the mass increase for every 7 polished stones is: D. 9.8 g.
What is the slope-intercept form?In Mathematics and Geometry, the slope-intercept form of the equation of a straight line is given by this mathematical equation;
y = mx + c
Where:
m represent the slope or rate of change.x and y are the points.c represent the y-intercept or initial value.Based on the information provided above, a linear equation that models the mass in grams is given by;
y = mx + c
m = 1.4p
By substituting the given parameter (x = 7 polished stones), we have the following:
m = 1.4(7)
m = 9.8 g
Read more on slope-intercept here: brainly.com/question/7889446
#SPJ4
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

Related Questions
Question2 of 25If ASTU AABC, which congruences are true by CPCTC? Check all that apply.

Answers
If triangle STU ≅ triangle ABC, then ∠T ≅ ∠B, ∠S ≅ ∠A, and segment TU ≅ Segment BC are true by CPCTC. Option A, option B, and option D are correct.
Let's understand what is the congruence of the triangle.
If all three corresponding sides are equal and all three corresponding angles are identical in measure, two triangles are said to be congruent. These triangles can be moved, rotated, flipped, and turned to look exactly the same.
CPCTC stands for corresponding parts of congruent triangles are congruent.
Let's check in the triangle STU and triangle ABC;
triangle STU ≅ triangle ABC
So,
∠S ≅ ∠A
∠T ≅ ∠B
∠U ≅ ∠C
segment ST ≅ Segment AB
segment TU ≅ Segment BC
segment SU ≅ Segment AC
Thus, if triangle STU ≅ triangle ABC, then ∠T ≅ ∠B, ∠S ≅ ∠A, and segment TU ≅ Segment BC are true by CPCTC. Option A, option B, and option D are correct.
To learn more about the congruence of the triangle visit:
https://brainly.com/question/19258025
#SPJ9
Find the amplitude and period of the function f(x)= -2 sin x. Show work
Answers
The period of the function f(x) = -2 sinx is 2π. So to summarize, the amplitude of the function is -2 and the period is 2π.
The general form of a sinusoidal function is f(x) = A sin(Bx - C) + D, where A is the amplitude, B determines the period, C is the phase shift, and D is the vertical shift.
For the function f(x) = -2 sinx, we can see that the amplitude (A) is -2, since the coefficient of the sin function is -2. The amplitude represents the maximum distance the graph oscillates above and below the midline, so in this case, the graph oscillates between y = -2 and y = 2.
To find the period (B), we can use the formula T = 2π/B, where T is the period and B is the coefficient of x in the sin function. In this case, B = 1, so T = 2π/1 = 2π.
Therefore, the period of the function f(x) = -2 sinx is 2π. So to summarize, the amplitude of the function is -2 and the period is 2π.
For more such questions on function , Visit:
https://brainly.com/question/25638609
#SPJ11
(q014) how many of the twenty-five top-grossing films of 2017 in the united states were part of a movie franchise?
Answers
five out of of the twenty-five top-grossing films of 2017 in the united states were part of a movie franchise
If you were to attribute this film, that means you'd say that (something) caused the success of the movie Rocky. This question is basically asking what do you think made this movie a big hit? Personally, I'd say it's because of how the storyline and plot turned out. It's very intriguing and it doesn't just make the movie about boxing. The film adds some love between the protagonist and some other character, and not only that, but the movie teaches you something. Because Rocky lost to Apollo, Rocky didn't care. At least he still had Adrian. So, the movie teaches you that, even if you do lose, at least you still have something and/or someone with you.
learn more about of film here
https://brainly.com/question/14824318
#SPJ4
order histograms a, b, and c from least to most variable. explain your reasoning. 5. between histograms d and e, which exhibits more variability? explain your reasoning.
Answers
To order histograms a, b, and c from least to a most variable, we would need to look at the spread of the data in each histogram. In other words, we want to see how much the values in each histogram vary from one another.
Histogram A has a narrow peak and doesn't seem to have much variability - the values are all clustered relatively close together. Histogram b has a slightly wider peak and some values that are more spread out, so it exhibits more variability than a. Finally, histogram c has the widest peak and the most spread-out values, so it exhibits the most variability of the three. Therefore, we would order the histograms from least to a most variable as follows: a, b, c.
Step 1: Examine the range and shape of each histogram. Histograms with a smaller range and more uniform distribution will have lower variability, while histograms with a larger range and a more uneven distribution will have higher variability.
Step 2: Compare histograms A, B, and C. Observe the distribution of data and identify which has the smallest range, followed by the next smallest, and finally the largest range.
Step 3: After identifying the order, we can provide a concise explanation for the reasoning. For example, "Histogram A has the least variability because it has the smallest range and the most uniform distribution of data. Histogram B has more variability than A but less than C, as it has a slightly larger range and a less uniform distribution. Histogram C has the most variability due to its large range and highly uneven distribution of data."
For the second part of your question:
To determine which histogram (D or E) exhibits more variability, follow the same steps as above:
Step 1: Examine the range and shape of histograms D and E.
Step 2: Compare the two histograms to determine which has a larger range and a more uneven distribution of data.
Step 3: Explain your reasoning. For example, "Histogram D exhibits more variability than histogram E because it has a larger range and a more uneven distribution of data."
To know more about histograms:- https://brainly.com/question/30354484
#SPJ11
evaluate the line integral, where c is the given curve. c xeyz ds, c is the line segment from (0, 0, 0) to (4, 3, 2)
Answers
The value of line integral is: 73038
Line Integrals:A line integral is any integral that is evaluated over a path. There are several ways to go about evaluating a line integral. Since our path is a simple line segment.
The parametric equations for the line segment from (0, 0, 0) to (2, 3, 4)
x(t) = (1-t)0 + t × 2 = 2t
y(t) = (1-t)0 + t × 3 = 3t
z(t) = (1-t)0 + t × 4 = 4t
We have to differentiation w.r.t "t"
x'(t) = 2
y'(t) = 3
z'(t) = 4
The given line integral is:
\(\int\limits_C {xe^y^z} \, ds=\int\limits^1_0 2te^1^2^t^2\sqrt{2^2+3^3+4^2} \, dt\\\\ds = \sqrt{2^2+3^3+4^2} dt\)
Now, We have to solve the integration and we get :
\(\int\limits_C {xe^y^z} \, ds=\frac{\sqrt{29} }{12} (e^1^2-1)\)
=> 73037.99 ≈ 73038
Hence, the value of line integral is, 73038.
Learn more about Line integral at:
https://brainly.com/question/30763905
#SPJ4
69% of all students at a college still need to take another math class. If 37 students are randomly selected, find the probability that a. Exactly 26 of them need to take another math class. b. At most 27 of them need to take another math class. c. At least 23 of them need to take another math class. d. Between 20 and 25 (including 20 and 25) of them need to take another math class. Hint:
Answers
We are asked to find the probability of different scenarios when 37 students are randomly selected.By using the binomial probability formula and the appropriate ranges, we can calculate the probabilities.
(a) To find the probability that exactly 26 students need to take another math class, we can use the binomial probability formula:
P(X = k) = (nCk) * (p^k) * ((1-p)^(n-k))
where n is the number of trials, k is the number of successes, p is the probability of success, and (nCk) is the binomial coefficient. Plugging in the values, we get:
P(X = 26) = (37C26) * (0.69^26) * (0.31^(37-26))
(b) To find the probability that at most 27 students need to take another math class, we need to calculate the cumulative probability:
P(X ≤ 27) = P(X = 0) + P(X = 1) + ... + P(X = 27)
(c) To find the probability that at least 23 students need to take another math class, we can calculate the complement of the probability that fewer than 23 students need to take another math class:
P(X ≥ 23) = 1 - P(X < 23)
(d) To find the probability that between 20 and 25 students (including 20 and 25) need to take another math class, we need to calculate the cumulative probability:
P(20 ≤ X ≤ 25) = P(X = 20) + P(X = 21) + ... + P(X = 25)
By using the binomial probability formula and the appropriate ranges, we can calculate the probabilities for each scenario.
To learn more about binomial probability formula click here : brainly.com/question/12474772
#SPJ11
When using the distributive property, the expression
3(2x - 1) would be simplified to
Answers
Answer:
\(6x - 3\)
Step-by-step explanation:
consider downloading photomath
Yes I give brainless answer today please !!

Answers
Answer:
The first answer is the correct answer.
Step-by-step explanation:
You see, when you add 11 to 0, you get 11, and when you take 5 away you subtract it from the positive 11.
So you see, number 1 is your clearest choice.
Mark Brainliest like promised!!
Answer:
The first one.
Becky and Barbara are shopping for clothes. Becky bought dresses that cost $14.50 and $20 and a pair of flip-flops for $8.25. Barbara bought a blouse for $8.25, a skirt for $20 and a pair of jeans for $14.50. How much did the two women spend together?
Answers
Answer:
$85.50 dollars
Step-by-step explanation:
Becky bought a $14.50 and $20 dress, and a $8.25 pair of flipflops. That is $42.75 . Barbara bought differernt things but still spent the same amount of $42.75 . So if you add those up, it would be $85.50 that they have spent together. Hope this helps :)
Seven years ago, Mrs Grey decided to invest R18 000 in a bank account that paid simple interest at 4,5% p.a. 4.1.1 Calculate how much interest Mrs Grey has earned over the 7 years. 4.1.2 Mrs Grey wants to buy a television set that costs R27 660,00 now. If the average rate of inflation over the last 5 years was 6,7% p.a., calculate the cost of the television set 5 years ago. 4.1.3 At what rate of simple interest should Mrs Grey have invested her money 7 years ago if she intends buying the television set now using only her original investment of R18 000 and the interest earned over the last 7 years?
Answers
The interest earned by Mrs Grey over the 7 years is R5670. The cost of the television set 5 years ago was R20,600.
4.1.1 To calculate the interest earned by Mrs Grey over 7 years, we use the formula for simple interest: Interest = Principal x Rate x Time. Mrs Grey's principal is R18,000 and the rate is 4.5% per annum. The time is 7 years. Using the formula, we can calculate the interest as follows:
Interest = R18,000 x 0.045 x 7 = R5670. Therefore, Mrs Grey has earned R5670 in interest over the 7 years.
4.1.2 To calculate the cost of the television set 5 years ago, we need to account for the inflation rate. The cost of the television set now is R27,660. The average rate of inflation over the last 5 years is 6.7% per annum. We can use the formula for compound interest to calculate the original cost of the television set:
Cost 5 years ago = Cost now / (1 + Inflation rate)^Time
Cost 5 years ago = R27,660 / (1 + 0.067)^5 = R20,600. Therefore, the cost of the television set 5 years ago was R20,600.
4.1.3 To determine the rate of simple interest Mrs Grey should have invested her money at 7 years ago, we can use the formula for interest: Interest = Principal x Rate x Time. We know the principal is R18,000, the time is 7 years, and the interest earned is R5670. Rearranging the formula, we can solve for the rate:
Rate = Interest / (Principal x Time)
Rate = R5670 / (R18,000 x 7) ≈ 0.0448 or 4.48% per annum. Therefore, Mrs Grey should have invested her money at a rate of approximately 4.48% per annum to have earned enough interest to purchase the television set using only her original investment and the interest earned over the 7 years.
Learn more about simple interest here:
brainly.com/question/30964674
#SPJ11
Intersecting Secant (Exterior)
Find X =

Answers
Answer: x = 13
Step-by-step explanation: the equation to solve this is:
4 × (4 + 8) = 3 × (3 + x)
so we solve the first half of that:
4 × (4 + 8)
4 × 12
48
now we have:
48 = 3 × (3 + x)
so we switch the sides to make it easier and solve
3 × (3 + x) = 48
divide both sides by 3
3 × (3 + x) ÷ 3 = 48 ÷ 3
and get
3 + x = 16
now subtract 3 from both sides
3 + x = 16
-3 -3
and finally we get
x = 13
hope this helped :)
HURRY PLS URGENT! HIGHLY APPRECIATE.

Answers
Answer:
b = 18
The mortar is 17 times ( 3 / 8 ) tall.
The brick height is equal to 18 times ( 2 + ( 1 / 4 ) ).
I don't know the options, so you have to use those values.
Step-by-step explanation:
DecipheringThe question uses imperial units which are generally bad.
12 inches = 1 feet;
The height of the wall should be written in inches for convenience.
4 feet = 4 * 12 inches;
4 feet = 48 inches;
The wall is short 1 + ( 1 / 8 ) inches short of 4 feet.
48 inches - ( 1 + ( 1 / 8 ) inches ) = 46 + ( 7 / 8 ) inches;
Now that the wall is done let's do the bricks. The height of the bricks is 2 + ( 1 / 4 ) inches and the mortar is ( 3 / 8 ) inches tall. The amount of mortar is the number of bricks - 1 because nobody puts extra mortar on the top of the wall.
Algebralet b;
46 + ( 7 / 8 ) = b( 2 + ( 1 / 4 ) ) + ( b - 1 )( 3 / 8 );
375 / 8 = b( 9 / 4 ) + ( 3 / 8 )b - ( 3 / 8 );
375 / 8 = ( ( 9 / 4 ) + ( 3 / 8 ) )b - ( 3 / 8 );
375 / 8 = ( ( 18 / 8 ) + ( 3 / 8 ) )b - ( 3 / 8 );
375 / 8 = ( 21 / 8 )b - ( 3 / 8 );
Multiply both sides by 8 to get rid of those annoying fractions.
375 = 21b - 3;
Add 3 to both sides.
378 = 21b;
Divide both sides by 21.
18 = b;
darwin's geometric ratio of increase pertains specifically to
Answers
Darwin's geometric ratio of increase pertains specifically to the growth rate of populations in biological organisms. According to Darwin's theory of evolution, populations have the potential to increase exponentially over time if certain conditions are met. The geometric ratio of increase, often denoted as "r" or the intrinsic rate of natural increase, represents the factor by which a population multiplies during each reproductive cycle or generation.
In the context of natural selection, individuals with higher reproductive rates (higher r-values) have a greater chance of passing on their genetic traits to the next generation. Over time, this can lead to significant population growth and evolutionary changes within a species. However, the geometric ratio of increase is limited by various factors, such as availability of resources, competition, predation, and environmental constraints, which can result in a balance between population growth and environmental carrying capacity.
To learn more about organisms : brainly.com/question/13278945
#SPJ11
help please !! super urgent

Answers
cosine = adjacent/hypotenuse (remember soh cah toa)
cos Z = 24/26, simplify it to 12/13
:)
If f(x) = x4 − x3 + x2 and g(x) = −x2, where x ≠ 0, what is (f ⁄g)(x)? m
Answers
Answer:x − x^{2} − 1.
Step-by-step explanation:
.
Al considerar 52 m como la distancia entre dos puntos situados realmente 53.06 m
Answers
two angels added together to produce 90 degrees so it is?rightcomputamenty supplementaryvertical
Answers
When the measure of two angles add 90 degrees, then they are called complementary angles.
If S={a,b,c} with P(a)=2P(b)=3P(c), find P(a). 9. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c) and P(d)=P(e)=P(f)=0.1, find P(a). 10. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c), P(d)=P(e)=P(f), and P(d)=2P(a), find P(a). 11. If E and F are two disjoint events in S with P(E)= 0.2 and P(F)=0.4, find P(E∪F),P(E
c
), and P(E∩F). 12. Why is it not possible for E and F to be two disjoint events in S with P(E)=0.5 and P(F)=0.7? 13. If E and F are two disjoint events in S with P(E)= 0.4 and P(F)=0.3, find P(E∪F),P(F
c
),P(E∩F), P((E∪F)
c
), and P((E∩F)
c
). 14. Why is it not possible for S={a,b,c} with P(a)= 0.3,P(b)=0.4, and P(c)=0.5 ?
Answers
Since the total probability of the sample space S must be equal to 1, it is not possible for three events with probabilities that add up to more than 1 to form the sample space.
9. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c) and P(d)=P(e)=P(f)=0.1, find P(a).
Since P(a), P(b), and P(c) are equal, we can let P(a) = P(b) = P(c) = x.
Then, we know that P(d) = P(e) = P(f) = 0.1.
The total probability of the sample space S is equal to 1. So, we can write the equation:
P(a) + P(b) + P(c) + P(d) + P(e) + P(f) = 1
Substituting the given values, we get:
3x + 0.1 + 0.1 + 0.1 = 1
3x + 0.3 = 1
3x = 1 - 0.3
3x = 0.7
Dividing both sides by 3, we find:
x = 0.7/3
So, P(a) = 0.233.
10. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c), P(d)=P(e)=P(f), and P(d)=2P(a), find P(a).
Let P(a) = P(b) = P(c) = x. And let P(d) = P(e) = P(f) = y.
We also know that P(d) = 2P(a).
Using the equation for the total probability:
P(a) + P(b) + P(c) + P(d) + P(e) + P(f) = 1
We can substitute the given values:
3x + 3y = 1
We also know that P(d) = 2P(a):
y = 2x
Substituting this into the previous equation:
3x + 3(2x) = 1
3x + 6x = 1
9x = 1
Dividing both sides by 9, we find:
x = 1/9
So, P(a) = P(b) = P(c) = 1/9.
11. If E and F are two disjoint events in S with P(E)=0.2 and P(F)=0.4, find P(E∪F), P(Ec), and P(E∩F).
Since E and F are disjoint, their intersection, E∩F, is empty.
The probability of the union of two disjoint events is the sum of their individual probabilities:
P(E∪F) = P(E) + P(F) = 0.2 + 0.4 = 0.6
The complement of E, Ec, is the event that consists of all outcomes in S that are not in E.
The complement of an event has a probability equal to 1 minus the probability of the event:
P(Ec) = 1 - P(E) = 1 - 0.2 = 0.8
Since E and F are disjoint, their intersection, E∩F, is empty, so its probability is 0:
P(E∩F) = 0
12. It is not possible for E and F to be two disjoint events in S with P(E)=0.5 and P(F)=0.7 because the sum of their probabilities would exceed 1.
Since the total probability of the sample space S must be equal to 1, it is not possible for two events with probabilities that add up to more than 1 to be disjoint.
13. If E and F are two disjoint events in S with P(E)=0.4 and P(F)=0.3, find P(E∪F), P(Fc), P(E∩F), P((E∪F)c), and P((E∩F)c).
Since E and F are disjoint, their intersection, E∩F, is empty.
The probability of the union of two disjoint events is the sum of their individual probabilities:
P(E∪F) = P(E) + P(F) = 0.4 + 0.3 = 0.7
The complement of F, Fc, is the event that consists of all outcomes in S that are not in F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P(Fc) = 1 - P(F)
= 1 - 0.3
= 0.7
Since E and F are disjoint, their intersection, E∩F, is empty, so its probability is 0:
P(E∩F) = 0
The complement of the union of two events, (E∪F)c, is the event that consists of all outcomes in S that are not in the union of E and F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P((E∪F)c) = 1 - P(E∪F) = 1 - 0.7 = 0.3
The complement of the intersection of two events, (E∩F)c, is the event that consists of all outcomes in S that are not in the intersection of E and F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P((E∩F)c) = 1 - P(E∩F) = 1 - 0 = 1
14. It is not possible for S={a,b,c} with P(a)=0.3, P(b)=0.4, and P(c)=0.5 because the sum of their probabilities exceeds 1.
Since the total probability of the sample space S must be equal to 1, it is not possible for three events with probabilities that add up to more than 1 to form the sample space.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
a person tosses a coin 15 times. in how many ways can he get 3 heads?
Answers
A person tosses a coin 15 times. In how many ways can he get 3 heads? The answer is 455 ways.
To find the answer, we can use the formula for combinations, which is:
C(n, k) = n! / (k! * (n-k)!)
Where n is the total number of tosses, and k is the number of heads we want to get.
In this case, n = 15 and k = 3, so we can plug these values into the formula:
C(15, 3) = 15! / (3! * (15-3)!)
C(15, 3) = 15! / (3! * 12!)
C(15, 3) = (15 * 14 * 13 * 12!)/ (3! * 12!)
C(15, 3) = 455
So there are 455 ways to get 3 heads when tossing a coin 15 times.
Learn more about probability theory and combinatorics here:https://brainly.com/question/29601156
#SPJ11
Solve for x using the Quadratic Formula: x² − 6x + 9 = 0 (reference photo)
A: x = 6
B: x = 3
C: x = 1
D: x = 0

Answers
Step-by-step explanation:
The answer of this equation is x = 3
B:x=3
Step-by-step explanation:
x2-3x+9=0x(x-3)-3(x-3)(x-3)(x-3)x-3=0x=3David sells electronics and works for wages plus commission. He earns a 5% commission for every electronic item sold. Based on the information in the table, what would David earn in wages plus commission for both weeks combined? ($_________)

Answers
Answer:
$925
Step-by-step explanation:
Week 1
Wage : 10x30=$300
Commission: 2000 x 5% = $100
Week 2
Wage ; 10x40=$400
Commission : 2500 x 5$ = $125
Add all together to get the total income for both weeks
$300 + $100 + $400 + $125 = $925 for the two week period including wages plus commission
David earns $925 in wages plus commission for both weeks combined.
How to calculate the percentage of commission?To calculate the commission,
Multiply the sale price with the commission percentage and divide it by 100.
I.e., sale price × commission percentage/100
Calculation:The commission percentage for every electronic item sold = 5%
Week 1:
Wage = $10.00 × 30 = $300
Commission = $2000 × (5/100) = $100
Wage + Commission = $300 + $100 = $400
Week 2:
Wage = $10.00 × 40 = $400
Commission = $2500 × (5/100) = $125
Wage + Commission = $400 +$125 = $525
Thus, for both weeks,
Wage + commision = $400 + $525 = $925
So, David earns $925 in wages plus commission for both weeks combined.
Learn more about commission percentages here:
https://brainly.com/question/9436892
#SPJ2
a) estimate the area under the graph of f(x) = 5 cos(x) from x = 0 to x = /2 using four approximating rectangles and right endpoints. (round your answers to four decimal places.)
Answers
The estimated area under the graph of f(x) = 5 cos(x) from x = 0 to x = π/2 using four approximating rectangles and right endpoints is approximately 0.8916.
To estimate the area under the graph of f(x) = 5 cos(x) from x = 0 to x = π/2 using four approximating rectangles and right endpoints, we can use the right Riemann sum method.
The width of each rectangle, Δx, is given by the interval width divided by the number of rectangles.
In this case, Δx = (π/2 - 0)/4 = π/8.
To calculate the right endpoint values, we evaluate f(x) at the right endpoint of each rectangle.
For the first rectangle, the right endpoint is x = π/8.
For the second rectangle, the right endpoint is x = π/4.
For the third rectangle, the right endpoint is x = 3π/8.
And for the fourth rectangle, the right endpoint is x = π/2.
Now, let's calculate the area for each rectangle by multiplying the width (Δx) by the corresponding height (f(x)):
Rectangle 1: Area = f(π/8) * Δx = 5cos(π/8) * π/8
Rectangle 2: Area = f(π/4) * Δx = 5cos(π/4) * π/8
Rectangle 3: Area = f(3π/8) * Δx = 5cos(3π/8) * π/8
Rectangle 4: Area = f(π/2) * Δx = 5cos(π/2) * π/8
Now, let's calculate the values:
Rectangle 1: Area = 5cos(π/8) * π/8 ≈ 0.2887
Rectangle 2: Area = 5cos(π/4) * π/8 ≈ 0.3142
Rectangle 3: Area = 5cos(3π/8) * π/8 ≈ 0.2887
Rectangle 4: Area = 5cos(π/2) * π/8 ≈ 0
Finally, to estimate the total area, we sum up the areas of all four rectangles:
Total Area ≈ 0.2887 + 0.3142 + 0.2887 + 0 ≈ 0.8916
Therefore, the estimated area under the graph of f(x) = 5 cos(x) from x = 0 to x = π/2 using four approximating rectangles and right endpoints is approximately 0.8916.
To know more about endpoints refer here:
https://brainly.com/question/31398203#
#SPJ11
Can you determine the solution of the |4x−2|≥−6 without solving?
Answers
Answer:
|4x-2|">"-6
add 2 to both sides
4x">"-4
divide both sides by 4
x">"-1
the ">" means greater than or equal to, I just don't have that character on my keyboard
Step-by-step explanation:
so the answer is x is greater than or equal to -1
IN: (-∞,-1]
for number line: You would write the number line from -1-10
then, you would put a closed dot on negative one, with an arrow going to the right!
Hope this helped! <3
What is System Effectiveness, if Operational Readiness is 0.89, Design Adequacy is 95%, Availability is 98%, Maintainability is 0.93, and Mission Reliability is 0.99? a. 0.763 b. 0.881 c. 0.837 d. 0.820
Answers
The System Effectiveness is approximately 0.763.
To calculate the System Effectiveness, we need to multiply the values of Operational Readiness, Design Adequacy, Availability, Maintainability, and Mission Reliability.
System Effectiveness = Operational Readiness * Design Adequacy * Availability * Maintainability * Mission Reliability
Plugging in the given values:
System Effectiveness = 0.89 * 0.95 * 0.98 * 0.93 * 0.99
System Effectiveness ≈ 0.763
Therefore, the System Effectiveness is approximately 0.763.
The correct answer is a. 0.763.
To know more about Maintainability refer here:
https://brainly.com/question/32350776#
#SPJ11
Evaluate the expression 2a+3d
Answers
Answer:
Step-by-step explanation:
Nothing further can be done with this topic
So, your answer would have to be 2a+3d
Pls help
Write a story about temperatures that this expression could represent:
27 + (-11)
Answers
Answer:
2333
Step-by-step explanation:
what is the value of x
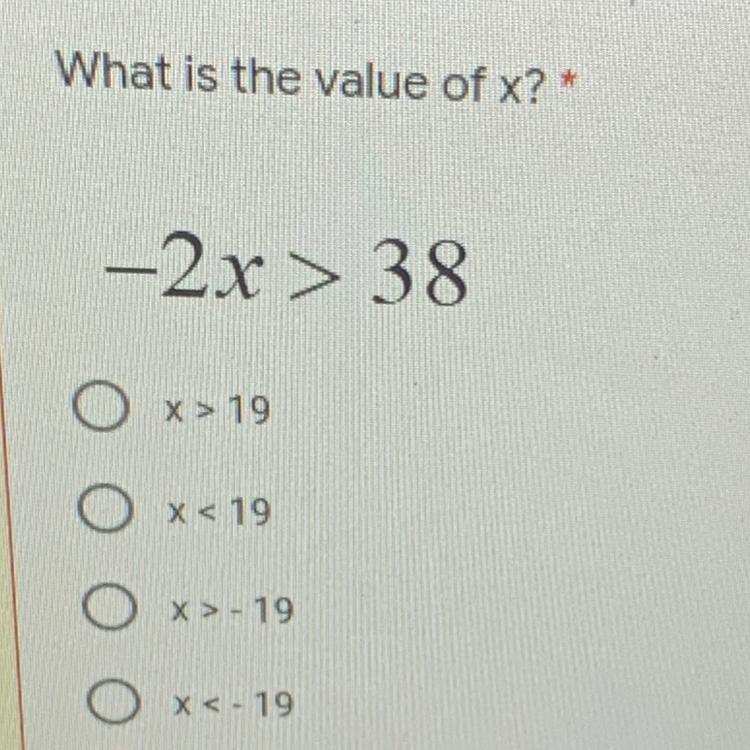
Answers
Answer:
x<-19
Step-by-step explanation:
hope that helps
Test for the commutative property of union and intersection of the sets P = { x : x is all real numbers between 2 and 7} and Q = { x : x is all rational numbers between 2 and 7}
Answers
Answer:
Step-by-step explanation:
P = {x : x is a real number between 2 and 7}
{x: 3,4,5,6}
Q = {x : x is all rational number between 2 and 7}
{4 }
We know that P contains all the rational numbers between 2 and 7.
And P ∪ Q and Q ∪ P each of them contain all the real numbers which are between 2 and 7.
{3,4,5,6}
Here Q is the proper subset of P
P ∩ Q = Q ∩ P = Q= {4}
there are 5 times as many tulips as rose bushes in a garden.there are 15 tulips . how many rose bushes are in the garden/
Answers
Answer:
There are 3 roses in the garden.
Step-by-step explanation:
If there are 5 times as man tulips in the garden as the roses, you would have to count 3, 5 times in order to get 15 which brings us to the answer of 3 roses in the garden.
what is the explicit rule for the nth term of the geometric sequence? 5, 20, 80, 320, 1,280, …
Answers
To determine the explicit rule for the nth term of the given geometric sequence 5, 20, 80, 320, 1,280, ..., use the formula:`an = a1 * r^(n - 1)`, where an represents the nth term of the sequence.`a1`represents the first term of the sequence.`r` represents the common ratio between terms of the sequence.
The given sequence is 5, 20, 80, 320, 1,280, ...Let's now apply the formula to find the explicit rule for the nth term of the given sequence.`an = a1 * r^(n - 1)`Where a1 = 5 (first term of the sequence)`r` can be found by dividing any term by the preceding term, as `r = (second term) / (first term)`In this case,`r = (20) / (5) = 4`
Substituting the values in the formula:`an = a1 * r^(n - 1)``an = 5 * 4^(n - 1)` Therefore, the explicit rule for the nth term of the given geometric sequence is `an = 5 * 4^(n - 1)`.You can use this formula to find the value of any term in the sequence, given its position (n) in the sequence.For example, to find the 150th term of the sequence, substitute n = 150 in the formula: `a150 = 5 * 4^(150 - 1)`. This simplifies to `a150 = 1.442 x 10^90`.
Learn more about geometric sequence
https://brainly.com/question/27852674
#SPJ11