Tashis money in her wallet how much money is remaining
Answers
Tashis originally had $100 in her wallet.
To find out how much money Tashis originally had in her wallet, we need to work backwards from the information given.
First, we know that she spent $60 on 1.5 kg of strawberries. This means that the price of the strawberries was $60 / 1.5 kg = $40 per kg.
Next, we know that she could have bought 2 kg of strawberries with the remaining money in her wallet. This means that she had $40/kg * 2 kg = $80 left in her wallet after the first purchase.
Finally, we know that she spent a fifth of her original amount on the first purchase. This means that $80 was four-fifths of her original amount. To find the original amount, we can set up the equation:
$80 = 4/5 * original amount
Multiplying both sides by 5/4 gives us:
$100 = original amount
Therefore, Tashis originally had $100 in her wallet.
Note: The question is incomplete. The complete question probably is: Tashis spent a fifth on the first purchase from the money in her wallet. From the remaining money, she could buy 2 kg of strawberries. But she purchased only 1.5 kg for $60. How much money was Marie originally in her wallet?
Learn more about Money:
https://brainly.com/question/3923016
#SPJ11
Related Questions
convert 36,400sec in day
Answers
Step-by-step explanation:
36400 sec = 0.421 day
I think this should be the answer
on exploration 4.3.3, what is a vertical asymptote for question 2?
Answers
A vertical asymptote is a line on the x-axis where the graph of a function approaches infinitely close but does not actually reach. In this case, the vertical asymptote is x = 4.
In exploration 4.3.3, the vertical asymptote for question 2 is at x = -2. Let's see what is meant by a vertical asymptote.What is a vertical asymptote?A vertical asymptote is a line that a function approaches but never touches.
The curve gets arbitrarily close to the vertical line but never touches it. When the function approaches a vertical asymptote, the function approaches infinity or negative infinity.For instance, consider the function f(x) = 1/x. It has a vertical asymptote at x = 0. This is because the function's value becomes increasingly larger as x approaches 0 from the positive side, and the value of the function becomes increasingly smaller as x approaches 0 from the negative side.Therefore, if a curve goes on increasing or decreasing on both sides of a vertical line (called a vertical asymptote), the curve approaches that line but never touches it. This is the basic idea of a vertical asymptote.What is the vertical asymptote for question 2?The rational function f(x) = (x + 2) / [(x + 2)^2 - 4] is being studied in question 2 of exploration 4.3.3. It can be seen that (x + 2)^2 - 4 = (x + 2 - 2)(x + 2 + 2) = (x)(x + 4).Therefore, the denominator (x + 2)^2 - 4 can be written as (x)(x + 4).The vertical asymptotes of a rational function occur where the denominator equals zero. Since the denominator is (x)(x + 4), the vertical asymptotes occur where x = 0 or x = -4.However, x = 0 is not a vertical asymptote because there is a hole in the graph. So, the only vertical asymptote is at x = -2. This means that the curve approaches x = -2 but never touches it. Therefore, the vertical asymptote for question 2 in exploration 4.3.3 is x = -2.
For more such asymptote related questions
https://brainly.com/question/28003042
#SPJ11
An article reported on a school​ district's magnet school programs. Of the 1882
qualified​ applicants, 987 were​ accepted, 309 were​ waitlisted, and 586
were turned away for lack of space. Find the relative frequency for each decision​ made, and write a sentence summarizing the results.
Answers
The school district's magnet school programs, of the 1882 qualified applicants, 52.44% were accepted, 16.41% were waitlisted, and 31.15% were turned away for lack of space.
The relative frequency for each decision made by the school district regarding their magnet school programs.
First, let's define relative frequency.
It is the fraction or proportion of the total data that belongs to a particular category or class. In this case, the categories are "accepted," "waitlisted," and "turned away."
To find the relative frequency for each decision, we need to divide the number of applicants in each category by the total number of qualified applicants, which is 1882.
So, the relative frequency for "accepted" is:
987/1882 = 0.524 or 52.4%
The relative frequency for "waitlisted" is:
309/1882 = 0.164 or 16.4%
And the relative frequency for "turned away" is:
586/1882 = 0.312 or 31.2%
To summarize the results, we can say that out of the 1882 qualified applicants for the school district's magnet school programs, 52.4% were accepted, 16.4% were waitlisted, and 31.2% were turned away due to lack of space.
This indicates that there is high demand for these programs and the school district needs to consider expanding their capacity to accommodate more students.
For similar question on school programs
https://brainly.com/question/21573814
#SPJ11
Given the function: f la!bldle ab ac ad cde Using Shannon's Expansion Theorem, what is (are) the cofactor(s) of f with respect to lab? ac cde d
la!b!dle !b!de
1 !d!e
C
Ab
Ad
b
Answers
1. When lab = 0: f_0 = f(lab = 0, cde, ac, ad) Here, we substitute lab with 0 in the function.
2. When lab = 1: f_1 = f(lab = 1, cde, ac, ad) Here, we substitute lab with 1 in the function.
So, the cofactors of the given function f with respect to lab are f_0 and f_1.
To find the cofactors of f with respect to lab using Shannon's Expansion Theorem, we need to consider two cases:
1. When lab = 0:
In this case, we need to remove the term that contains lab. So we can rewrite f as follows:
f = (ab ac ad) + (cde)
To find the cofactor of f with respect to lab = 0, we need to remove the terms that contain both lab and its complement (la!b):
Cofactor of f with respect to lab = 0 = (ac ad) + (cde) = acd + cde + ace + ade
2. When lab = 1:
In this case, we need to set lab to 1 and remove the term that contains its complement (la!b).
So we can rewrite f as follows: f = (ab ac ad) + (cde)
Setting lab to 1 gives us: f|lab=1 = ac ad cde
To find the cofactor of f with respect to lab = 1, we need to remove the terms that contain both lab and its complement (la!b):
Cofactor of f with respect to lab = 1 = ad cde
Therefore, the cofactors of f with respect to lab are acd + cde + ace + ade and ad cde.
Using Shannon's Expansion Theorem, we can determine the cofactors of the given function f with respect to the variable lab.
The theorem states that any function can be expressed as the sum of its cofactors.
Visit here to learn more about Cofactors:
brainly.com/question/12120216
#SPJ11
If AD = 5.1cm, find the height (in cm) of the triangle.

Answers
Answer:
I. AC = 15 cm
II. h = 7.4 cm
Step-by-step explanation:
I. Determination of AC
AB = 9 cm
BC = 12 cm
AC =?
The length AC can be obtained by using pythagoras theory as illustrated below:
AC² = AB² + BC²
AC² = 9² + 12²
AC² = 81 + 144
AC² = 225
Take the square root of both side
AC = √225
AC = 15 cm
II. Determination of the height.
AB = 9 cm
AD = 5.1 cm
BD = h =?
The height of the triangle can be obtained by using pythagoras theory as illustrated below:
AB² = AD² + BD²
9² = 5.1² + h²
81 = 26.01 + h²
Collect like terms
h² = 81 – 26.01
h² = 54.99
Take the square root of
h = √54.99
h = 7.4 cm
The parametric equations x=t+1 and y=t^2+2t+3 represent the motion of an object. What is the shape of the graph of the equations? what is the direction of motion?
A. A parabola that opens upward with motion moving from the left to the right of the parabola.
B. A parabola that opens upward with motion moving from the right to the left of the parabola.
C. A vertical ellipse with motion moving counterclockwise.
D. A horizontal ellipse with motion moving clockwise.
Answers
Answer:
A) A parabola that opens upward with motion moving from the left to the right of the parabola.
Step-by-step explanation:
\(x=t+1\rightarrow t=x-1\\\\y=t^2+2t+3\\y=(x-1)^2+2(x-1)+3\\y=x^2-2x+1+2x-2+3\\y=x^2+2\)
Therefore, we can see that the shape of the graph is a parabola that opens upward with motion moving from the left to the right of the parabola.
Find the slope of the line that passes through the pair of points
(-13,7) and (1, -14)
Answers
Answer:
m= -3/2
Step-by-step explanation:
I hope this helps

A circle has a radius of 50 cm. Which of these is closest to its area?
Answers
Answer:
Approximately 7853.98
Step-by-step explanation:
The formula to finding the area of a circle based on radius is \(\pi r^2\\\), where r is radius. Hope this helped :D
Please HELPPPPPPPP jkskjqinunuanuanunwuniam
Answers
Answer:
kakss ke sjene oeejrneme kenej ok?
Step-by-step explanation:
42 divided by (15-2 to the 3rd power) someone smart and fast help me! Please
Answers
42/ (15-8)
42/7
6
The value of the number expression 42 divided by (15-2 to the 3rd power) or 42 ÷ (15 - 2³) is 6.
What is an integer exponent?In mathematics, integer exponents are exponents that should be integers. It may be a positive or negative number. In this situation, the positive integer exponents determine the number of times the base number should be multiplied by itself.
It is given that:
42 divided by (15-2 to the 3rd power)
Mathematically,
= 42 ÷ (15 - 2³)
After applying the properties of integer exponent:
= 42 ÷ (15 - 8)
Because 2³ = 8
= 42 ÷ 7
After dividing
= 6
Thus, the value of the number expression 42 divided by (15-2 to the 3rd power) or 42 ÷ (15 - 2³) is 6.
Learn more about the integer exponent here:
brainly.com/question/4533599
#SPJ2
Solve the following quadratic equation for all values of x in simplest form.
3(x-5)^2=33
Answers
The value of x for the given quadratic expression is x = 5 ± √11.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given expression is 3(x-5)²=33. The value of x will be calculated as,
3(x-5)²=33
(x - 5 )² = 11
(x - 5 ) = ±√11
x = 5 ± √11
Therefore, the value of x for the given quadratic expression is x = 5 ± √11.
To know more about an expression follow
https://brainly.com/question/27826679
#SPJ1
x^2-4x^2y^2+y^2+2*x*y
Answers
Answer:
(x + y - 2xy)*(x + y + 2xy)
Step-by-step explanation:
x^2-4x^2y^2+y^2+2*x*y
=x^2 + 2xy + y^2 - (2xy)^2
=(x + y)^2 - (2xy)^2
=(x + y - 2xy)*(x + y + 2xy)
A new bank customer with $3,000 wants to open a money market account. The bank is offering a simple interest rate of 1.8%. How much interest will the customer earn in 10 years? b. What will the account balance be after 10 years?
Answers
Answer: See explanation
Step-by-step explanation:
The Simple Interest will be calculated as:
= P × R × T
= $3000 × 1.8% × 10.
= $3000 × 0.018 × 10
= $540
The interest that the customer earn in 10 years is $540.
Then, the account balance after 10 years will be:
= Principal + Interest
= $3000 + $540
= $3540
Therefore, the account balance will be $3540
A.)19
B.)132
C.)48
D.)21

Answers
Answer:
Hello! answer: 48
Step-by-step explanation:
3 × 19 - 9 = 48
7 × 19 - 1 = 132
48 + 132 = 180 so... 48 is the measure of ABC
Answer:
C.) 48
Step-by-step explanation:
I seem like it's multiple choice, I don't think you really need an explanation
PLEASE! HELP ASAP GIVING 100 POINTS AND BRAINLEST!
Write a system of equations to compare these two scenarios:
1) You buy a grande café latte from Starbucks every day, which costs 3.65
2) You spend 300 to buy an espresso machine and purchase supplies for lattes, which cost an additional 1.35 a day.
a) After how many days will the price of buying lattes for Starbucks equal the price of making lattes at home?
b) How much money will you have spent at this point?
Answers
The equations used to compare the two scenarios are as follows:
3.65x
300 + 1.35x
What is an equation?Identifying which variables values result in equality is part of solving a variable equation. The variables for which the equation must be solved are known as unknowns, whereas the unknown values that fulfill the equality are known as equation solutions. A mathematical expression with two equal sides separated by an equal sign is known as an equation. 4 + 6 = 10. We can see 4 + 6 on the left and 10 on the right side of the equal symbol.
We already have,
1) You often purchase a grande cafe latte from Starbucks, which costs $3.65.
This formula is:
Number of days = x
Total cost after x days = 3.65x
2) You spend $300 on an espresso machine and ingredients for lattes, which cost an extra $1.35 per day.
This formula is:
Number of days = x
Total cost after x days = 300 + 1.35x
Now, three days later,
3.65 x 3 = $10.95
300 + 1.35 x 3 = 300 + 4.05 = $304.05
Thus,
The equations used to compare the two scenarios are as follows:
3.65x
300 + 1.35x
To know more about equation, visit:
https://brainly.com/question/29538993
#SPJ1
Traveling carnivals move from town to town, staying for a limited number of days before moving to the next stop. The management of a certain carnival knows that each
time it opens in a new town, it can expect to bring in about $15,000 in revenue the first night. Each night after the first revenue will be about 75% of the previous night's
revenue.
To the nearest dollar, about how much revenue can the carnival anticipate on its 5th night in town?
Answers
Answer: 4746.09375 dollars (just round down to nine cents)
Step-by-step explanation:
The revenue in the 5th night in two will be $4746.093.
What is geometrical progression series?A geometric progression is a sequence in which any element after the first is obtained by multiplying the previous element by a constant which is called a common ratio denoted by r.
For example, the sequence 1, 4, 16, 64,… is a geometric sequence with a common ratio of r = 4.
Revenue in the first night = $15000
Since revenue of new night is 75% of the previous night
So,
2nd night = 15000 × 75/100 = 11250
3rd night = 8437.5
So the given sequence is ;
15000, 11250, 8437.5 ... it is a GP series.
First term(a) = 15000
Common ratio(r) = 11250/15000 = 0.75
The nth term of a GP is given by ;
\(a_{n} = ar^{n-1}\)
So for 5th-night n = 5
So,
a₅ = ar⁵⁻¹
a₅ = 15000(0.75)⁴
a₅ = 4746.093
Hence "The revenue in the 5th night in two will be $4746.093".
For more information about the geometrical progression,
brainly.com/question/4853032
#SPJ2
3(x + 1) + 2 ???????
Answers
Answer:
I love algebra anyways
the ans is in the picture with the steps
(hope it helps can i plz have brainlist :D hehe)
Step-by-step explanation:

Twelve months of sales data are provided in the table below
along with the associated seasonal relatives. This product
experiences a seasonal pattern that repeats every year. Create a
linear regressio
Answers
Linear regression is a technique used in statistics and machine learning to understand the relationship between two variables and how one affects the other.
In this case, we are interested in understanding the relationship between sales and seasonality. We can use linear regression to create a model that predicts sales based on seasonality. Here's how we can do it First, let's plot the data to see if there is a relationship between sales and seasonality.
We can see that there is a clear pattern that repeats every year. This indicates that there is a strong relationship between sales and seasonality. We can use the following equation: y = mx + b, where y is the dependent variable (sales), x is the independent variable (seasonality), m is the slope of the line, and b is the intercept of the line.
To know more about technique visit :
https://brainly.com/question/31609703
#SPJ11
2x + 4 = 16 Please Identify the following. What number is the coefficient? What is the variable? What is the constant?
Answers
Explanation: The coefficient is a number in front of your variable.
So here, the coefficient is 2 since it's before the variable x.
A variable is a letter that represents any number.
So here, the variable or the letter is x.
The constant is the number on its own.
So here, we have two constants, they are 4 and 16.
2.) South High School has 820 students. There are 40 more boys than girls. How many girls are
there? How many boys are there?
Answers
Foundation Geometry
midpoint of AC
A. 18
B. 6
C.27
D.54

Answers
Answer:
D
Step-by-step explanation:
Since B is the midpoint of AC , then
AB = BC , substitute values
4x + 3 = 3x + 9 ( subtract 3x from both sides )
x + 3 = 9 ( subtract 3 from both sides )
x = 6
Then
AC = AB + BC
= 4x + 3 + 3x + 9
= 7x + 12
= 7(6) + 12
= 42 + 12
= 54 → D
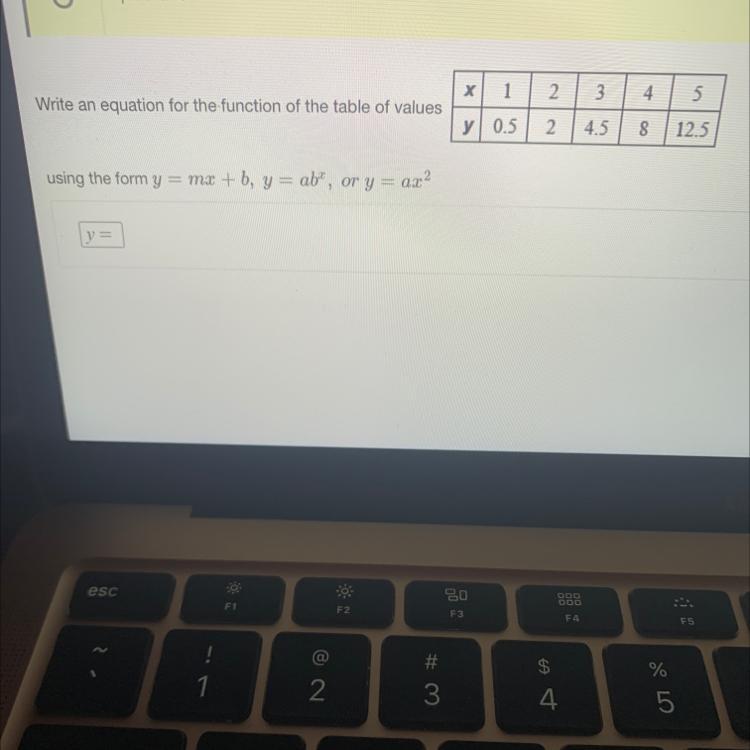
Can someone help me with this math problem?
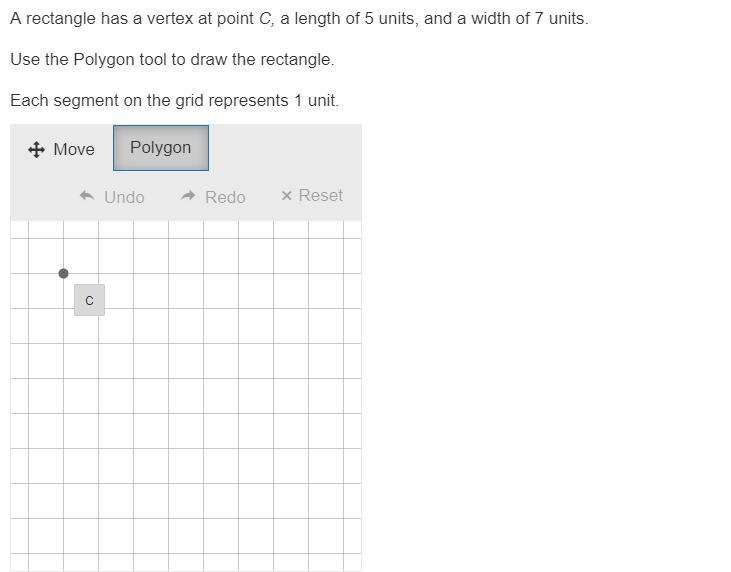
Answers
Answer:
Add a dot (Point A) 5 units to the left of point C, a dot (Point B) 7 units below point C, and a final dot (Point D) that is 5 units across from Point B
Step-by-step explanation:
Using the definition of a rectangle (4 right angles)
- Length is usually viewed as left to right
- Width is usually viewed as top to bottom

The covariance between the returns of A and B is -0. 112. The standard deviation of the rates of return is 0. 26 for stock A and 0. 81 for stock B. The correlation of the rates of return between A and B is closest to: A. )-1. 88 B. )-. 53 C. ). 53 D. )1. 88
Answers
The correlation of the rates return between stock A and B for the given covariance and standard deviation is given by option B. -0.53.
Covariance between stock A and B = -0.112
Standard deviation of the rates return for stock A = 0.26
Standard deviation of the rates return for stock B = 0.81
Formula for correlation in terms of covariance and standard deviations is
Correlation = covariance / (standard deviation of A x standard deviation of B)
Here correlation of the rates of return between A and B.
Substitute the given values we get,
⇒ Correlation = (-0.112) / (0.26 x 0.81)
⇒ Correlation ≈ -0.430769 / 0.81
⇒ Correlation ≈ -0.5318
⇒ Correlation ≈ -0.53
Therefore, the correlation of the rates of return between A and B is is equal to option B. -0.53.
Learn more about correlation here
brainly.com/question/30725780
#SPJ4
what easier way can you find out 8 times 9?
Answers
Answer & Step-by-step explanation:
8 is 2×2×2.
Doubling a number is the same as multiplying ×2.
So maybe you could take the 9 and double it, 18.
Double it again, 36.
Double it again, 72.
Or anyway that you can "take apart" 8 and 9 in smaller numbers and rearrange, because you can multiply in any order.
For example, if you don't know your 8 or 9 times tables, but you know your 3 and 4 and 6 times tables:
8 is 4×2 and
9 is 3×3.
8×9 is the same as 2×3 and 4×3
6×12
which is 72.
Hope this helps.
Find the value of x. Round to the nearest tenth.

Answers
Answer:
x = 10.8
Step-by-step explanation:
Cos∅ = adj/hyp
Cos26 = x/12
Multiply both sides by 12
12 * cos26 = x
Use calculator
10.785528555590004 = x
Round
x = 10.8
Find the missing side. Round to the nearest tenth. Will give Brainliest.
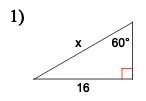
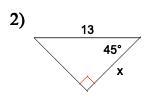
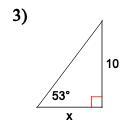
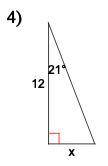
Answers
Answer:
Answers are below.
Step-by-step explanation:
Sin θ = Opposite / Hypotenuse
Cos θ = Adjacent / Hypotenuse
Tan θ = Opposite / Adjacent
1) sin (60) = 16/x
x = 16/(sin 60)
x ≈ 18.46
2) cos (45) = x/13
13 cos(45) = x
x ≈ 9.19
3) tan (53) = 10/x
x = 10/tan(53)
x ≈ 7.54
4) tan (21) = x/12
12 tan(21) = x
x ≈ 4.61
Use the Gram-Schmidt process to find orthonormal bases for the spaces a) span{(512),(−46)}; 2. (a) {131(512),131(−125)};
Answers
(a) The orthonormal basis for the space span{(5,12),(−4,6)} is {(5/13, 12/13), (-92/26√(13), 90/26√(13))}. (b) The orthonormal basis for the space span{13/1(5,12), 13/1(−1, 2, -5)} is {(5/13, 12/13), (6/26√(13), 358/26√(13), 6/26√(13))}.
(a) To find an orthonormal basis for the space span{(5,12),(−4,6)}, we can apply the Gram-Schmidt process:
Step 1: Normalize the first vector.
v₁ = (5, 12)
u₁ = v₁ / ||v₁|| = (5, 12) / √(5² + 12²) = (5/13, 12/13)
Step 2: Subtract the projection of the second vector onto the first vector.
v₂ = (−4, 6)
u₂ = v₂ - proj(u₁, v₂)
First, find the projection of v₂ onto u₁:
proj(u₁, v₂) = (v₂ · u₁) * u₁ = ((−4, 6) · (5/13, 12/13)) * (5/13, 12/13)
= (-20/13 + 72/13) * (5/13, 12/13)
= (52/13) * (5/13, 12/13)
= (20/13, 48/13)
Then, subtract the projection from v₂:
u₂ = v₂ - (20/13, 48/13) = (-4, 6) - (20/13, 48/13)
= (-4, 6) - (20/13, 48/13)
= (-4 - 20/13, 6 - 48/13)
= (-92/13, 90/13)
Step 3: Normalize u₂ to obtain the second vector in the orthonormal basis.
u₂ = (-92/13, 90/13) / ||(-92/13, 90/13)|| = (-92/13, 90/13) / √((-92/13)² + (90/13)²)
= (-92/13, 90/13) / (2√(13))
Therefore, the orthonormal basis for the space span{(5,12),(−4,6)} is {(5/13, 12/13), (-92/26√(13), 90/26√(13))}.
(b) To find an orthonormal basis for the space span{13/1(5,12), 13/1(−1, 2, -5)}, we can apply the Gram-Schmidt process:
Step 1: Normalize the first vector.
v₁ = (13/1)(5, 12)
u₁ = v₁ / ||v₁|| = (13/1)(5, 12) / √((13/1)²(5² + 12²))
= (5/√(5² + 12²), 12/√(5² + 12²))
= (5/13, 12/13)
Step 2: Subtract the projection of the second vector onto the first vector.
v₂ = (13/1)(-1, 2, -5)
u₂ = v₂ - proj(u₁, v₂)
First, find the projection of v₂ onto u₁:
proj(u₁, v₂) = (v₂ · u₁) * u₁
= (((13/1)(-1, 2, -5)) · (5/13, 12/13)) * (5/13, 12/13)
= (-1(5/13) + 2(12/13), -5(5/13) + 2(12/13), -1(5/13) - 5(12/13))
= (-19/13, -14/13, -77/13)
Then, subtract the projection from v₂:
u₂ = v₂ - (-19/13, -14/13, -77/13)
= (13/1)(-1, 2, -5) + (19/13, 14/13, 77/13)
= (13/1)(-1, 2, -5) + (19/13, 14/13, 77/13)
= (-13/1 + 19/13, 26/1 + 14/13, -65/1 + 77/13)
= ((-1313 + 19)/13, (2613 + 14)/13, (-65*13 + 77)/13)
= (6/13, 358/13, 6/13)
Step 3: Normalize u₂ to obtain the second vector in the orthonormal basis.
u₂ = (6/13, 358/13, 6/13) / ||(6/13, 358/13, 6/13)||
= (6/13, 358/13, 6/13) / √((6/13)² + (358/13)² + (6/13)²)
= (6/13, 358/13, 6/13) / (26√(13))
Therefore, the orthonormal basis for the space span{13/1(5,12), 13/1(−1, 2, -5)} is {(5/13, 12/13), (6/26√(13), 358/26√(13), 6/26√(13))}.
To know more about orthonormal basis,
https://brainly.com/question/32955526
#SPJ11
I pull the throttle in my racing plane at a = 12.0 m/s2. i was originally flying at v = 100. m/s. where am i when t = 2.0, t = 5.0, and t=10.0?
Answers
The distance covered by plane when t = 2s will be 176m and when t = 5s will be 350m and when t = 10s will be 400m found using equation of motion.
We have,
Acceleration of plane i.e. a = 12 m/s²
And,
Velocity of plane i.e. v = 100 m/s
And,
t₁ = 2s
t₂ = 5s
t₃ = 10s
So,
Now,
Using the equation of motion,
i.e.
S = vt - \(\frac{1}{2}\) at²
Here,
S = Distance,
v = initial velocity,
a = acceleration
t = time taken
Now,
For t₁ = 2s,
Putting values in above equation we get,
S = (100 * 2) - (\(\frac{1}{2}\) * 12 * 2²)
On solving we get,
S = 200 - 24 = 176 m,
So,
Plane will be at 176m distance.
Now,
For t₂ = 5s,
Putting values in above equation we get,
S = (100 * 5) - (\(\frac{1}{2}\) * 12 * 5²)
On solving we get,
S = 500 - 150 = 350 m,
So,
Plane will be at 350m distance.
Now,
For t₃ = 10s,
Putting values in above equation we get,
S = (100 * 10) - (\(\frac{1}{2}\) * 12 * 10²)
On solving we get,
S = 1000 - 600 = 400 m,
So,
Plane will be at 400m distance.
Hence, we can say that the distance covered by plane when t = 2s will be 176m and when t = 5s will be 350m and when t = 10s will be 400m found using equation of motion.
To learn more about equation of motion click here
https://brainly.com/question/12114762
#SPJ4
please assist with helping in the image below!!

Answers
What can we conclude if the omnibus null hypothesis is rejected in a one-factor anova?
Answers
Answer:
Not all the means are equal.
Step-by-step explanation:
In an ANOVA table, a sum of squares for the independent variable divided by its respective degrees of freedom.
So if the omnibus null hypothesis is rejected it means that there is sufficient evidence to conclude that not all the means are equal.
https://brainly.com/question/13045159
#SPJ4
If the omnibus null hypothesis is rejected in a one-factor ANOVA, then, we can conclude that at least one of the population means is different from at least one other population mean.
ANOVA table gives us the total sum of squares ( TSS ), the residual sum of squares ( RSS ) and the estimated sum of squares ( ESS ).
It establishes the relation that:
ESS + RSS = TSS.
If we reject the omnibus null hypothesis, then it means that:
at least one of the population means is different from at least one other population mean.
Therefore, we get that, if the omnibus null hypothesis is rejected in a one-factor ANOVA, then, we can conclude that at least one of the population means is different from at least one other population mean.
Learn more about ANOVA here:
https://brainly.com/question/15084465
#SPJ9