Sherri saves nickels and dimes in a coin purse for her daughter. The total value of the coins in the purse is $0.70. The number of nickels is two less than six times the number of dimes. How many nickels and how many dimes are in the coin purse?
Answers
Answer:
Therefore, there are 10 nickels in the coin purse.
Step-by-step explanation:
Let's call the number of dimes in the coin purse "D" and the number of nickels "N".
We know the total value of the coins in the purse is $0.70, which we can express in cents as 70 cents:
5N + 10D = 70
We also know that the number of nickels is two less than six times the number of dimes:
N = 6D - 2
We can substitute the second equation into the first equation to get an equation with only one variable:
5(6D - 2) + 10D = 70
Simplifying this equation, we get:
30D - 10 + 10D = 70
Combining like terms, we get:
40D = 80
Dividing both sides by 40, we get:
D = 2
So there are 2 dimes in the coin purse.
Using the equation N = 6D - 2, we can find the number of nickels:
N = 6(2) - 2 = 10
Therefore, there are 10 nickels in the coin purse.
Related Questions
Can you please help me thanks

Answers
Answer:
b . all of the other ones look the same and that one is the different one
Answer:
B
Step-by-step explanation:
A proportional relationship graph should be a straight line, no curves.
B Which expression is equivalent to -5 × 4?
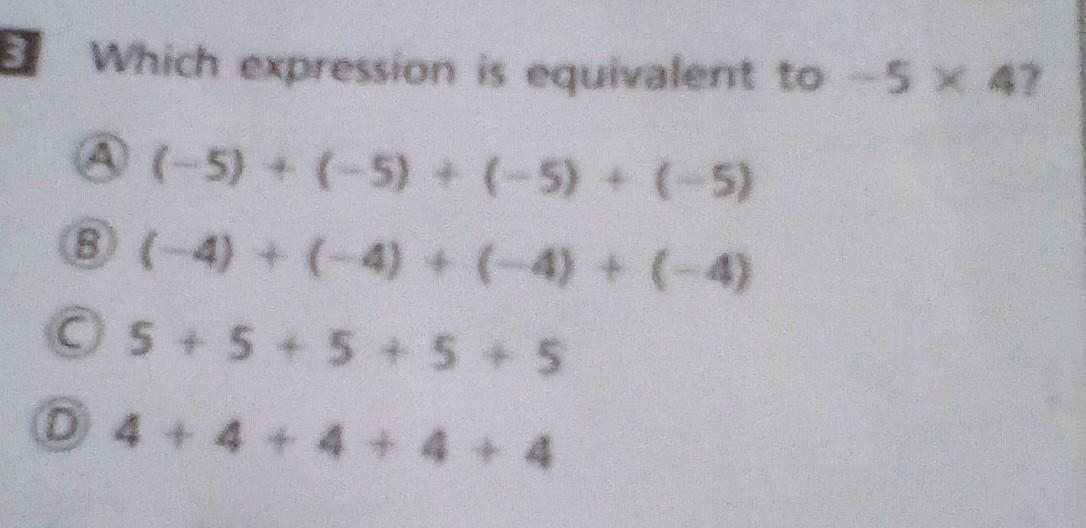
Answers
Answer: A
Step-by-step explanation:
-5+-5+-5+-5=-20
-4+-4+-4+-4=-16
5+5+5+5+5=25
4+4+4+4+4=20
The questions asks for -5 x 4 = -20
absolute value of -1/6
Answers
You get this answer because this is how far away from zero it is
One side of a square is 33 inches long. The area of the square is _ square inches.

Answers
The area of the square is 1084 square inches.
What is the area of a square?The area of a square can be calculated as the square of the sides of a given figure. A square is always a rectangle, parallelogram, a rhombus and a quadrilateral but its reverse statement may or may not be true.(ie it is not always necessary that a rectangle is a square or a parallelogram is a square or a rhombus is a square).
The area of a square = side x side
Given;
One side of square= 33inches
Area of square= A^2
=33x33
=1089
Therefore, the area will be 1089m^2
More about the area of the square link is given below.
brainly.com/question/1658516
#SPJ1
What is -6(-3+5r)=-5-7r
Answers
Answer:
r = 1
Step-by-step explanation:
Use the distributive property to multiply −6 by −3+5r.
18−30r=−5−7r
Add 7r to both sides.
18−30r+7r=−5
Add −30r and 7r to get −23r.
18−23r=−5
Subtract 18 from both sides.
−23r=−5−18
Subtract 18 from −5 to get −23.
−23r=−23
Divide both sides by −23.
r=−23/−23
Divide −23 by −23 to get 1.
r=1
[-12] + [4] find the absolute value of each integer then add them
Answers
Hello there!
Answer:
16
Step-by-step explanation:
\( |x| = x \: \: \: if \: \: x \: \geqslant 0 \\ |x| = - x \: \: \: if \: \: \: x \: \leqslant 0\)
-12 < 0 so |-12| = -(-12) = 12
4 > 0 so |4| = 4
|-12| + |4| = 12 + 4 = 16
Answer:
16
Step-by-step explanation:
Hello! This question is looking for the absolute value of integers. The absolute value is the distance the number has from zero. For example, -12 as twelve numbers away from zero, twelve away in the negative direction. The absolute value of -12, then, is just twelve. An easy way to remember this is to take away the negative sign when taking the absolute value, since an absolute value can never be negative. The absolute value sign is represented by a squarish bracket [ and ].
This question says to find the absolute value of each integer and then add the two. First we have [-12]. This is 12 away from zero, and we can take away the - sign from the asked integer and we get 12.
The second integer given is 4, and when we take the absolute value of 4, [+4], we get positive four. This is because four is four spaces away from zero on the number line.
Thus, we have +12 and +4 as are values to add since they are the absolute values and we can form this equation
12+4=16
Thus, the answer is 16.
Hope this helps! Remember the hint, when something has brackets like that or asks for the absolute value, take away a negative sign and make it positive! Have a great day!
Two turtles, Velma and Justine, were entered into a race.
The equation y = 4x represents Velma's distance in meters, y, after racing for x minutes. The graph below displays Justine's distance and time.
Based on the equation and graph, which two statements below are true?
A.Justine is twice as fast as Velma.
B. Justine is half as fast as Velma.
C. Justine and Velma have the same speed.
D. Justine moves a greater distance than Velma each minute.
E. Justine moves a shorter distance than Velma each minute.

Answers
Answer:
B and E
Step-by-step explanation:
the graph (Justine) shows the line
y = 2x
the line for Velma is
y = 4x
now we need to remember that the slope (inclination) of a line is the factor of x (so, 2 and 4 in the two line equations).
a slope is expressed as y/x and indicates how many units y changes when x changes a certain amount of units (like 1).
as described (and also confirmed by the graph) the x units are minutes, and the y units are meters.
so, as per her slope, Velma moves 4 meters in 1 minute.
and Justine moves 2 meters in 1 meter.
so, Justine is half as fast as Velma.
and therefore, Justine moves a shorter distance than Velma each minute.
Answer:
Step-by-step explanation:
B and E
Math Homework: Unit 3 Assignment

Answers
Convert 21 inches to feet using dimensional analysis round to 2 decimal places necessary

Answers
1 foot = 12 inches = 1/12
21/1 x 1/12 = 21/12 = 1.75 feet
Answer: 1.75 feet
f(x)=3^x+1 and g(x) = 2x-4, find f(2) - g(-1)
Answers
Answer:
16
Step-by-step explanation:
3^x +1 = f(X)
2x-4 = g(x)
find f(2)-g(-1)
we substitute in function f(X) by value (2), and in function g(X) by value (-1)
1. 3^x +1 becomes 3^2+1 =9+1=10
2. 2(-1)-4= -2-4=-6
then f(2)-g(-1)
= 10-(-6) =10+6=16
Someone help with this equation

Answers
The answer is:
g(x + 1) = 6x + 1
g(4x) = 24x -5
Work/explanation:
To evaluate, I plug in x + 1 into the function:
\(\sf{g(x)=6x-5}\)
\(\sf{g(x+1)=6(x+1)-5}\)
Simplify
\(\sf{g(x+1)=6x+6-5}\)
\(\sf{g(x+1)=6x+1}\)
------------------
Do the same thing with g(4x)
\(\sf{g(4x)=6(4x)-5}\)
\(\sf{g(4x)=24x-5}\)
Hence, these are the answers.
Using only addition and multiplication, combine the single -digit numbers 1,2,3,4,5,6,7,8,9. So they total 100. the number must stay in the same order (Parentheses are not needed)
Answers
It is not possible to find a combination using addition and multiplication of the given single-digit numbers that totals exactly 100 while keeping the same order.
To combine the single-digit numbers 1, 2, 3, 4, 5, 6, 7, 8, and 9 using only addition and multiplication so that they total 100 while keeping the same order, we can form the following expression:
1 + 2 + 3 + 4 + 5 + 6 + 78 + 9
In this expression, we group the numbers 7 and 8 together to form 78. Then, we add all the other numbers from 1 to 6 and the number 9. Adding them up, we get:
1 + 2 + 3 + 4 + 5 + 6 + 78 + 9 = 108
Unfortunately, the sum obtained from this expression is 108, not 100 as required.
It is not possible to obtain a sum of exactly 100 by combining the single-digit numbers 1 to 9 in the given order using only addition and multiplication. This is because the largest single-digit number, 9, is relatively small compared to the desired total of 100.
Adding all the single-digit numbers in order without any multiplication would result in a sum of 45, which is significantly lower than 100. Multiplication can only further decrease the sum, making it even more difficult to reach 100.
For more such question on combination visitr;
https://brainly.com/question/28065038
#SPJ8
Weekly wages at a certain factory are
normally distributed with a mean of
$400 and a standard deviation of $50.
Find the probability that a worker
selected at random makes between
$300 and $350.
[ ? ]%
Answers
The probability that a worker selected at random makes between $300 and $350 is 0.1359 Or 13.6%.
What is a normal distribution?A probability distribution that is symmetric about the mean is the normal distribution, sometimes referred to as the Gaussian distribution. It demonstrates that data that are close to the mean occur more frequently than data that are far from the mean.
Given, Weekly wages at a certain factory are normally distributed.
Mean(\(\overline{x}\)) = 400, S.D(\(\sigma\)) = 50.
Now, Since the wages are normally distributed we know,
\(z = \frac{x - \overline{x}}{\sigma}\).
Therefore,
z = (300 - 400)/50.
z = - 2.
And
z = (350 - 400)/2.
z = - 1.
Now, from the z-table,
P(z ≤ - 2) = 0.0228 and P(z ≤ - 1) = 0.1587.
Combining the two we have P( - 2 ≤ z ≤ - 1) = 0.1587 - 0.0228.
P( - 2 ≤ z ≤ - 1) = 0.1359.
As a result, the likelihood that a randomly chosen employee will earn between $300 and $350 is 0.1359, or 13.6%.
learn more about normal distributions here :
https://brainly.com/question/29509087
#SPJ1
Your iron works has contracted to design and build a 500-ft^3, square-based, open-top, rectangular steel holding tank for a paper company. The tank is made by welding thin stainless steel plates together along their edges. As the production engineer, your job is to find dimensions for the base and height that will make the tank weigh as little as possible. How will you take weight into account?
What dimensions do you tell the shop to use?
Answers
The dimensions we will tell the shop to use are ⇒ Volume = 10 x 10 x 5 foot
The surface area of the box = \(225\) \(ft^{2}\)
Weight of the metal = 1125 kg
According to the question,
Given value = \(500\) \(ft^{3}\) tanks is to be built which has to be a square-based rectangle steel holding tank.
For this, we have to know the total surface area of the box,
Surface area (A) = 4 x sides of the rectangle + square base -- equation 1
Let's take the width of the square base = p
And let height = h
Since we know that,
Rectangle sides = p x h
Square base ⇒ p x p = \(p^{2}\)
Substituting these values in equation 1,
Surface area ( A ) = 4 x ( p x h ) + \(p^{2}\) ---- equation 2
The formula for calculating the volume of the box,
V = p x p x h
V = \(p^{2}\) x h --- equation 3
Referring to the question that the value of the volume is already given such that volume = \(500\) \(ft^{3}\)
So, V = \(500\) \(ft^{3}\)
Putting the value of V in equation 3,
500 = \(p^{2}\) x h
h = \(\frac{500}{p^{2} }\) ---- equation 4
Substituting the value of h from equation 4 to equation 2,
A = 4 x ( p x \(\frac{500}{p^{2} }\) ) + \(p^{2}\)
⇒ A = \(\frac{2000}{P}\) + \(p^{2}\)
We will be taking the derivative of the above equation,
⇒ A' = - \(\frac{2000}{p^{2} }\) + 2p
Now we will be minimizing A,
⇒ 0 = - \(\frac{2000}{p^{2} }\) + 2\(p\)
⇒ \(\frac{2000}{p^{2} }\) = 2\(p\)
⇒ 2000 = 2\(p^{3}\)
⇒ 1000 = \(p^{3}\)
⇒ p = \(\sqrt[3]{1000}\)
⇒ p = 10 foot
Substituting the value of p in equation 4,
⇒ h = \(\frac{500}{10^{2} }\)
⇒ h = \(\frac{500}{100}\)
⇒ h = 5 foot
Substituting values in the area of the square box,
A = 4 x (10 x 5) + \(5^{2}\)
A = 200 + 25
A = 225 \(ft^{2}\)
The weight of the metal,
⇒ weight = A x weight per square foot
⇒ weight = 225 x 5
⇒ weight = 1125 kg
Therefore, The dimensions we will tell the shop to use are ⇒ Volume = 10 x 10 x 5 feet
The surface area of the box = 225 \(ft^{2}\)
To learn more about area and dimension,
https://brainly.com/question/27057965
#SPJ4
Let f(x) = x2 − 2x + 1. Find the inverse function of f by identifying an appropriate restriction of its domain.
Answers
Answer: \(f^{-1} (x) = \sqrt{x} +1\)
Step-by-step explanation:
\(y = x^2 - 2x + 1\)
We know straight away the inverse will be a square root function. We also know that this inverse will have a restriction on the domain, (because you can only take the square root of a positive number).
So, to find the inverse, first we'll switch the x and y and solve for y:
\(x = y^2 - 2y +1\)
\(x = (y-1)^2\), (factor!)
±\(\sqrt{x} = y - 1\)
So, the inverse "function" is:
\(f^-1(x)\) = ±\(\sqrt{x} +1\)
But theres an issue here!
If we tried graphing this, this "function" would not pass the vertical line test, so its not really a function at all!
We need to restrict the domain to only include the values that are above the x axis.
So our final inverse function is:
\(f^{-1} (x) = \sqrt{x} +1\)
suppose that a sphere passes through the point and has center . (a) find the distance between the points and
Answers
The distance between two points in three-dimensional space is a measure of the separation between the two points. In this case, the two points are the center of a sphere and a point that the sphere passes through.
To find the distance, we can use the distance formula in three dimensions, which is an extension of the distance formula in two dimensions. The distance formula is:
d = √((x1 - x2)^2 + (y1 - y2)^2 + (z1 - z2)^2)
where (x1, y1, z1) is the center of the sphere and (x2, y2, z2) is the point that the sphere passes through. The square root of the sum of the squares of the differences between the corresponding coordinates gives the distance between the two points.
In this problem, the center of the sphere is not given, so it is not possible to calculate the distance between the sphere and the point. The center of the sphere is a crucial piece of information needed to solve this problem.
to know more about Geometry
https://brainly.com/question/24375372
#SPJ4
HELLPPPPPPPPP PLEAAASSSEEEEE

Answers
Write the equation of the line fully simplified slope-intercept form.

Answers
Answer:
x+5
Step-by-step explanation:
If a varies as square root of y, how x is affected when y is increased by 44%
Answers
Answer: 16.7%
Step-by-step explanation:
x/(root y) =x
root y is increased by 44%
x/(44+root y)=16.7%
Plz help with these 2 questions and thx !

Answers
Answer:
The first is 18.
The second is less than (<).
Step-by-step explanation:
Hope this helps <3
Answer:
1. 18
2. C
Step-by-step explanation:
1. 7/42=1/6 3•6=18
2. 3/7 is greater than 3/8
A cylinder has a height of 20 cm and a diameter of
6 cm. What is the volume, in cubic centimeters, of the
cylinder? Use 3.14 for T.
Answers

This question is designed to be answered without a calculator.
If f(x) = 5(x2 – 1), thenLimit of StartFraction f (x) minus f (2) Over x minus 2 EndFraction as x approaches 2 =
0.
5.
10.
20.
Answers
The limit of [f(x) - f(2)]/[x - 2] as x approaches 2 is 20
How to evaluate the limit as it approaches 0From the question, we have the following function that can be used in our computation:
f(x) = 5(x2 – 1)
Rewrite as
f(x) = 5(x² – 1)
The limit is given as
[f(x) - f(2)]/[x - 2]
Calculate f(2)
So, we have
f(2) = 5(2² – 1)
Evaluate
f(2) = 15
Substitute f(2) = 15 in [f(x) - f(2)]/[x - 2]
So, we have
[f(x) - f(2)]/[x - 2] = [5(x² – 1) - 15]/[x - 2]
Open the brackets
[f(x) - f(2)]/[x - 2] = [5x² – 5 - 15]/[x - 2]
Evaluate the like terms
[f(x) - f(2)]/[x - 2] = [5x² – 20]/[x - 2]
Factorize
[f(x) - f(2)]/[x - 2] = [5(x² – 4)]/[x - 2]
Express as difference of two squares
[f(x) - f(2)]/[x - 2] = [5(x – 2)(x + 2)]/[x - 2]
Divide
[f(x) - f(2)]/[x - 2] = 5(x + 2)
Limit x to 2
[f(x) - f(2)]/[x - 2] = 5(2 + 2)
Evaluate
[f(x) - f(2)]/[x - 2] = 20
Hence, the limit is 20
Read more about function limits at
https://brainly.com/question/26103899
#SPJ1
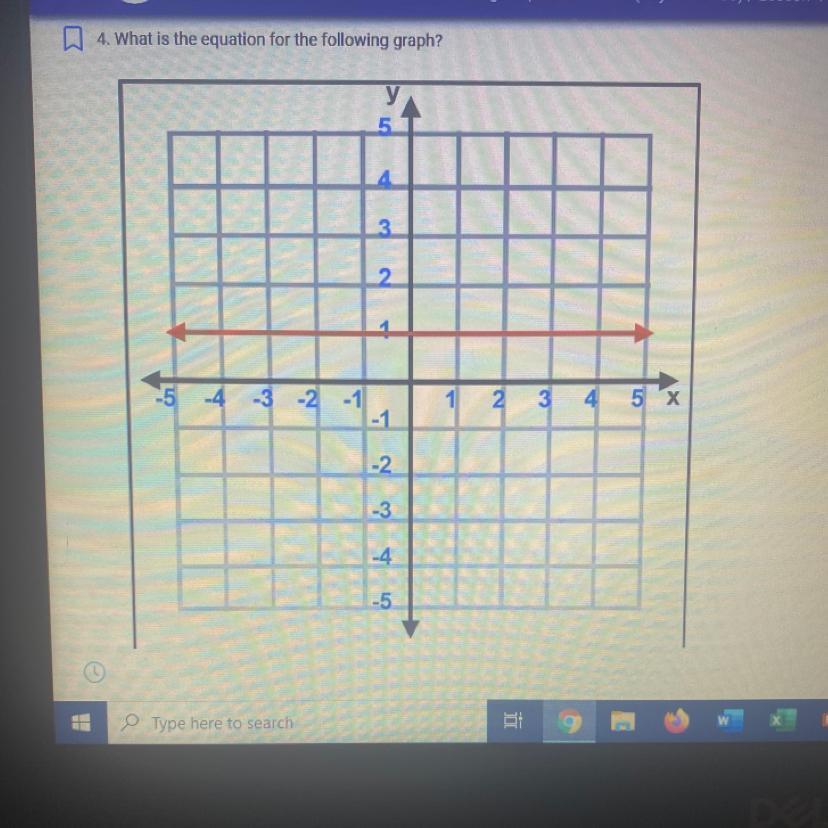
Hello I could use help please :) the answer solutions are- y=-1, y=1 , x=1 , x=-1
Answers
Take into account that for horizontal lines, the equation of the graph has the general form y = c, where c is the value of y where x = 0, or the y-intercept.
As you can notice in the given line and based on the previous description, you have:
y = 1
A game has an expected value to you of $. It costs $ to play, but if you win, you receive $100,000 (including your $ bet) for a net gain of $. What is the probability of winning? Would you play this game? Discuss the factors that would influence your decision.
Answers
The probability of winning this game is 0.003
How to solve for the probability of winningLet us name p to be the probability of winning the game.
We have the expected value to be 100
100 = probability of winning + 1-p x loss
win = 100000 - 200
We then input in the formula
100 = p*99800 +(1-p) x -200
100 = 99800p - 200 + 200p
Collect like terms
100 + 200 = 99800 + 200p
300 = 100000p
Divide through by 100000
This give the
Probability of winning = 0.003
The probability of winning the game is very low hence I would not play.
The factors that would influence the decision are:
The cost of playingThe expected valueComplete questionA game has an expected value to you of ?$100. It costs ?$200 to? play, but if you win you receive? $100,000 (including your ?$200 ?bet), for a net gain of ?$99,800. What is the probability of? winning
Read more on probability here:
https://brainly.com/question/24756209
#SPJ1
Let (1=1,2,3, 4, 5, 6, 7, 8, 9, 10

Answers
The list of elements in the sets are as follows:
A. A ∩ B = {2, 9}
B. B ∩ C = {2, 3}
C. A ∪ B ∪ C = {1, 2, 3, 5, 7, 8, 9, 10}
D. B ∪ C = {2, 3, 5, 7, 9, 10}
How to find the elements in a set?Set are defined as the collection of objects whose elements are fixed and can not be changed.
Therefore,
universal set = U = {1,2,3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 7, 8, 9}
B = {2, 3, 5, 9}
C = {2, 3, 7, 10}
Therefore,
A.
A ∩ B = {2, 9}
B.
B ∩ C = {2, 3}
C.
A ∪ B ∪ C = {1, 2, 3, 5, 7, 8, 9, 10}
D.
B ∪ C = {2, 3, 5, 7, 9, 10}
learn more on set here: https://brainly.com/question/29484130
#SPJ1
Garden table and bench is 657 total. Garden table is $43 less than bench. What cost of bench?
Answers
Answer:
$350
Step-by-step explanation:
Let the bench cost $x
Then the garden table costs $x - 43
x + (x - 43) = 657
2x = 657 + 43
2x = 700
x = 350
The cost of the bench is $350.
Nice day to you!
Find the dimensions of the rectangular garden of greatest area that can be fenced off (all four sides) with 300 meters of fencing.
Answers
The dimensions of the rectangular garden to maximize the area is length = width = 75 meters.
Let l be the length and w be the width of the rectangular garden.
We need to find the dimensions of the rectangular garden of greatest area that can be fenced off (all four sides) with 300 meters of fencing.
The perimeter of the rectangular garden = 300 meters
We know that the perimeter of the rectangle =2(length + width)
300 = 2(l + w)
l + w = 150 .......(1)
Now, the maximum area of a rectangular garden is when Length = width
So, for equation 1
l + l = 150
l = 75 meters
So, w = 75 meters
And the area of the rectangular garden = length * width
= 75 * 75
= 5625 m²
So the maximum area of the rectangular garden is 5625 m²
Therefore, the dimensions of the garden to maximize the area is length = width = 75 meters and maximum area is 5625 m²
Learn more about rectangles here:
brainly.com/question/16021628
#SPJ4
how do I understand implicit function
Answers
Answer: An implicit function is a function, written in terms of both dependent and independent variables, like y-3x2+2x+5 = 0. Whereas an explicit function is a function which is represented in terms of an independent variable.
Step-by-step explanation: To find the implicit derivative,
Differentiate both sides of f(x, y) = 0 with respect to x.
Apply usual derivative formulas to differentiate the x terms.
Apply usual derivative formulas to differentiate the y terms along with multiplying the derivative by dy/dx.
Solve the resultant equation for dy/dx (by isolating dy/dx).
What are electrophillic substitution reaction
Answers
The examples of electrophilic substitution reactions are:
Halogenation Nitration. Sulphonation.What are electrophilic substitution reactions?An atom that is connected to an aromatic ring is replaced with an electrophile in electrophilic aromatic substitution processes.
An electrophilic substitution reaction can be seen as the chemical process in which an electrophile replaces the functional group belonging to a molecule. which can be regraded as the atom of hydrogen which makes up the displace functional group.
Learn more about reactions at;
https://brainly.com/question/11231920
#SPJ9
complete question;
What are electrophillic substitution reaction?
A.Halogenation
B.Redox reaction
C. Nitration.
D. Sulphonation.
△ABC has vertices A(-2, 0), B(0,8), and C(4,2) Find the equations of the three altitudes of △ABC
Answers
The equations of the three altitudes of triangle ABC include the following:
3y - 2y - 4 = 0.y + 3x - 8 = 0.4y + x - 6 = 0.What is a triangle?A triangle can be defined as a two-dimensional geometric shape that comprises three (3) sides, three (3) vertices and three (3) angles only.
What is a slope?A slope is also referred to as gradient and it's typically used to describe both the ratio, direction and steepness of the function of a straight line.
How to determine a slope?Mathematically, the slope of a straight line can be calculated by using this formula;
\(Slope, m = \frac{Change\;in\;y\;axis}{Change\;in\;x\;axis}\\\\Slope, m = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}\)
Also, the point-slope form of a straight line is given by this equation:
y - y₁ = m(x - x₁)
Assuming the following parameters for triangle ABC:
Let AM be the altitudes on BC.Let BN be the altitudes on CA.Let CL be the altitudes on AB.For the equation of altitude AM, we have:
Slope of BC = (2 - 8)/(4 - 0)
Slope of BC = -6/4
Slope of BC = -3/2
Slope of AM = -1/slope of BC
Slope of AM = -1/(-3/2)
Slope of AM = 2/3.
The equation of altitude AM is given by:
y - y₁ = m(x - x₁)
y - 0 = 2/3(x - (-2))
3y = 2(x + 2)
3y = 2x + 4
3y - 2y - 4 = 0.
For the equation of altitude BN, we have:
Slope of CA = (2 - 0)/(4 - (-2))
Slope of CA = 2/6
Slope of CA = 1/3
Slope of BN = -1/slope of CA
Slope of BN = -1/(1/3)
Slope of BN = -3.
The equation of altitude BN is given by:
y - y₁ = m(x - x₁)
y - 8 = -3(x - 0)
y - 8 = -3x
y + 3x - 8 = 0.
For the equation of altitude CL, we have:
Slope of AB = (8 - 0)/(0 - (-2))
Slope of AB = 8/2
Slope of AB = 4
Slope of CL = -1/slope of AB
Slope of CL = -1/4
The equation of altitude CL is given by:
y - y₁ = m(x - x₁)
y - 2 = -1/4(x - 4)
4y - 2= -(x - 4)
4y - 2= -x + 4
4y + x - 2 - 4 = 0.
4y + x - 6 = 0.
In conclusion, we can infer and logically deduce that the equations of the three altitudes of triangle ABC include the following:
3y - 2y - 4 = 0.y + 3x - 8 = 0.4y + x - 6 = 0.Read more on point-slope form here: brainly.com/question/24907633
#SPJ1