Answers
Capacitors and inductors (which might be from time to time known as reactors) are passive gadgets that generate or soak up reactive strength.
They accomplish this with out widespread real-strength losses or running expense. The output of capacitors and inductors is proportional to the rectangular of the voltage. Voltage magnitudes are in large part decided via way of means of reactive strength flows;
Reactive strength go with the drift on the road will increase the voltage distinction among sending and receiving buses; • The more potent the short-circuit strength in a given bus, the much less reactive strength go with the drift from the road reduces its voltage with appreciate to the sending bus reactive strength go with the drift thru a transmission line is proportional to the cosine of the section perspective distinction among the sending and receiving give up voltages.
Read more about transmission:
https://brainly.com/question/24373056
#SPJ4
Related Questions
How many tons and pounds (like together, not two different numbers) is 9,920 pounds? Please help,
Answers
Answer:
About 5 tons (4.96)
A truck with mass m has a brake failure while going down an icy mountain road of constant downward slope angle α (Figure 1). Initially the truck is moving downhill at speed v0. After careening downhill a distance L with negligible friction, the truck driver steers the runaway vehicle onto a runaway truck ramp of constant upward slope angle β. The truck ramp has a soft sand surface for which the coefficient of rolling friction is μr.
What is the distance that the truck moves up the ramp before coming to a halt? Solve using energy methods.
Express your answer in terms of m , α , v0 , L , g , β and μr .
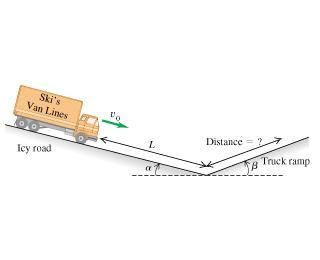
Answers
((v² ÷ 2g) + LSinα) ÷ (Sinβ + µcosβ) is the distance that the truck moves up the ramp before coming to a halt.
Let the distance the truck moves up the ramp be by x.
The kinetic energy of the truck on an icy road is given by,
K1 = (1÷2)mv²
The potential energy of the truck on an icy road is given by,
U1 = mgLSinα
The kinetic energy of the truck on the tuck ramp is given by,
K2 = 0
The potential Energy of the truck-on-truck ramp is given by,
U2 = mgxSinβ
Work done is given by,
W(others) = -µ×mg×cosФ
Hence, by using the work-energy theorem,
W(others) = (K2 + U2)(K1 + U1)
Therefore, by putting the values we get,
((1÷2)mv² + mgLSinα)(0 + mgxSinβ) = -µ×mg×cosФ
x = (K1 + mgLSinα) ÷ (mg(Sinβ + µcosβ))
x = ((v² ÷ 2g) + LSinα) ÷ (Sinβ + µcosβ)
Learn more about velocity-time the at
https://brainly.com/question/16178738?referrer=searchResults
#SPJ9
From shortest to longest wavelength, which of the following correctly orders the different categories of electromagnetic radiation?
A.gamma rays, X rays, ultraviolet, visible light, infrared, radio
B. infrared, visible light, ultraviolet, X rays, gamma rays, radio
C. gamma rays, X rays, visible light, ultraviolet, infrared, radio
D. radio, infrared, visible light, ultraviolet, X rays, gamma rays
Answers
The following correctly orders the different categories of electromagnetic radiation; Radio, infrared, visible light, ultraviolet, X rays, gamma rays.
What is the ultraviolet?Ultraviolet (UV) radiation is a type of electromagnetic radiation emitted from the sun. It is a form of energy that is invisible to the human eye, but it can cause damage to living organisms. UV radiation is divided into three categories: UVA, UVB, and UVC. UVA radiation has the longest wavelength and is the least hazardous form of UV radiation. UVB radiation has a shorter wavelength and is more dangerous. UVC radiation has the shortest wavelength and is the most dangerous form of UV radiation. Exposure to UV radiation can cause sunburns, premature skin aging, and an increased risk of skin cancer.
To learn more about ultraviolet
https://brainly.com/question/1377878
#SPJ4
Most towns use a water tower to store water and provide pressure in the pipes that deliver water to customers. The figure below shows a spherical water tank that holds 5.80 105 kg of water when full. Note that the tank is vented to the atmosphere at the top and that the pipe delivering water to customer Smith is a height h = 3.75 m above the level of the pipe delivering water to customer Jones. Determine the gauge pressure of the water at the faucet of each house when the tank if full.
There is a spherical water-filled chamber with a vent on top and underneath it is a pipe 18 m long that leads down to the ground. At ground level a horizontal pipe connects the faucet in the Jones house to the water supply. The faucet in the Smith house is connected to the water supply with a pipe at a height h above ground level.
(a) Jones house
Pa
(b) Smith house
Pa
Answers
The effective height of the water for Smith's house will be 24.61m.
How to calculate the height?Based on the information given, the volume of the water in sphere will be:
= 4/3πr³ = (5.80 × 10^5)/1000
= 4.18r³ = 580
r³ = 138.7
r = 5.18m
The effective height of the water will be:
= 18.0 + 2(5.18)
= 28.36
The gauge pressure at Faucet of Jones house will be:
= pgh
= 1000(9.8)(28.36)
= 277.9kPa
The effective height of the water for Smith's house will be:
= 18.0 + 2(5.18) - 3.75
= 24.61m
The gauge pressure at Faucet of Jones house will be:
= 1000 × 9.8 × 24.61
= 241.2kPa
Learn more about height on:
brainly.com/question/983412
#SPJ1
Answer #49 please and thank you

Answers
when Force (N) is 10.0 Length (m) is 0.60
when Force (N) is 8.0 Length (m) is 0.40
when Force (N) is 4.0 Length (m) is 0.20
when Force (N) is 4.0 Length (m) is 0.20
when Force (N) is 2.0 Length (m) is 0.10
chatgpt
49. To find the length of a pendulum that has a period of 2.3 seconds on the Moon, where the gravitational acceleration (g) is 1.6 N/kg, we can use the formula:
Period (T) = 2π√(Length (L) / g)
Substituting the given values:
2.3 = 2π√(L / 1.6)
To solve for L, we can rearrange the formula:
L = (2.3 / (2π))^2 * 1.6
L ≈ 0.781 meters (or 78.1 centimeters)
So, the pendulum must be approximately 0.781 meters (or 78.1 centimeters) long to have a period of 2.3 seconds on the Moon.
50. Ranking Task:
To rank the pendulums according to their periods, we need to consider both the length and mass of each pendulum.
Ranking from least to greatest period:
1. A: 10 cm long, mass = 0.25 kg
2. C: 20 cm long, mass = 0.25 kg
3. B: 10 cm long, mass = 0.35 kg
There is a tie between pendulums A and C, as they have the same length but different masses.
If air resistance exerts a constant force of 200 N on a car, what amount of forward force from the engine is
needed to make a 1000 kg car accelerate at 10 m/s² forward? Is this force constant or increasing?
Answers
The forward force is 10200 N.
What is the forward force?The term "forward force" is not commonly used as a specific term, but it could refer to any force that acts in the direction of motion of an object. For example, the force generated by a car's engine that propels it forward is commonly referred to as the "driving force," which could be considered a type of forward force.
We have to note that the Fnet = ma
= 1000 * 10 = 10000 N
Thus;
Fnet = Force force - Resistance force
Forward force = Fnet + Resistance force
= 10000 + 200
= 10200 N
Learn more about force:https://brainly.com/question/13191643
#SPJ1
The amount of forward force from the engine needed to make the 1000 Kg car accelerate 10 m/s² forward is 10200 N
How do I determine the forward force needed to accelerate the car?First, we shall obtain the net force acting on the 1000 Kg car. Details below:
Mass of car (m) = 1000 KgAcceleration of car (a) = 10 m/s²Net force (F) =?Net force = mass × acceleration
Net force = 1000 × 10
Net force = 10000 N
Finally, we shall obtain the forward force needed to accelerate the car. This is illustrated below:
Net force = 10000 NResistant force = 200 NForward force = ?Net force = Forward force - resistant force
10000 = Forward force - 200
Collect like terma
Forward force = 10000 + 200
Forward force = 10200 N
Thus, the forward force needed is 10200 N
Learn more about force and acceleration:
https://brainly.com/question/12163222
#SPJ1
if a certain car, going with speed v1, rounds a level curve with a radius r1, it is just on the verge of skidding. if its speed is now doubled, the radius of the tightest curve on the same road that it can round without skidding is:
Answers
Answer:
The correct answer is 4R1
Explanation:
According to the given scenario ,the radius of the tightest curve on the same road without skidding is as follows:
As we know that
Centeripetal Acceleration is
= v^2 ÷ r
In the case when velocity becomes 2 times so the r would be 4 times
So, the radius of the tightest curve on the same road without skidding is 4R1
A boy lifts a 30N toy car 2 meters above the ground. How much work did the boy do on the car?
Answers
30x2=60
hope this helps
In the US, the conventional voltage seen in a recepticle (wall outlet) is 120 V. How many amperes is required to run a stereo that has a resistance of 494 capital omega ?
Answers
Given that the voltage is V = 120 V
The resistance is
\(R\text{ =494 }\Omega\)We have to find the current.
Current in the circuit can be calculated by the formula,
\(I=\frac{V}{R}\)Substituting the values, the current will be
\(\begin{gathered} I=\frac{120}{494} \\ =0.24\text{ A} \end{gathered}\)Convert 7,348 grams to kilograms
Answers
Can someone explain how to do the algebra for this question? I know everything else, I just don’t know how to rearrange the question to solve for v.

Answers
Answer:
Refer to the step-by-step Explanation.
Step-by-step Explanation:
Simplify the equation with given substitutions,
Given Equation:
\(mgh+(1/2)mv^2+(1/2)I \omega^2=(1/2)mv_{_{0}}^2+(1/2)I \omega_{_{0}}^2\)
Given Substitutions:
\(\omega=v/R\\\\ \omega_{_{0}}=v_{_{0}}/R\\\\\ I=(2/5)mR^2\)\(\hrulefill\)
Start by substituting in the appropriate values: \(mgh+(1/2)mv^2+(1/2)I \omega^2=(1/2)mv_{_{0}}^2+(1/2)I \omega_{_{0}}^2 \\\\\\\\\Longrightarrow mgh+(1/2)mv^2+(1/2)\bold{[(2/5)mR^2]} \bold{[v/R]}^2=(1/2)mv_{_{0}}^2+(1/2)\bold{[(2/5)mR^2]}\bold{[v_{_{0}}/R]}^2\)
Adjusting the equation so it easier to work with.\(\Longrightarrow mgh+\dfrac{1}{2} mv^2+\dfrac{1}{2} \Big[\dfrac{2}{5} mR^2\Big]\Big[\dfrac{v}{R} \Big]^2=\dfrac12mv_{_{0}}^2+\dfrac12\Big[\dfrac25mR^2\Big]\Big[\dfrac{v_{_{0}}}{R}\Big]^2\)
\(\hrulefill\)
Simplifying the left-hand side of the equation:
\(mgh+\dfrac{1}{2} mv^2+\dfrac{1}{2} \Big[\dfrac{2}{5} mR^2\Big]\Big[\dfrac{v}{R} \Big]^2\)
Simplifying the third term.
\(\Longrightarrow mgh+\dfrac{1}{2} mv^2+\dfrac{1}{2} \Big[\dfrac{2}{5} mR^2\Big]\Big[\dfrac{v}{R} \Big]^2\\\\\\\\\Longrightarrow mgh+\dfrac{1}{2} mv^2+\dfrac{1}{2}\cdot \dfrac{2}{5} \Big[mR^2\Big]\Big[\dfrac{v}{R} \Big]^2\\\\\\\\\Longrightarrow mgh+\dfrac{1}{2} mv^2+\dfrac{1}{5} \Big[mR^2\Big]\Big[\dfrac{v}{R} \Big]^2\)
\(\\ \boxed{\left\begin{array}{ccc}\text{\Underline{Power of a Fraction Rule:}}\\\\\Big(\dfrac{a}{b}\Big)^2=\dfrac{a^2}{b^2} \end{array}\right }\)
\(\Longrightarrow mgh+\dfrac{1}{2} mv^2+\dfrac{1}{5} \Big[mR^2\Big]\Big[\dfrac{v^2}{R^2} \Big]\\\\\\\\\Longrightarrow mgh+\dfrac{1}{2} mv^2+\dfrac{1}{5} \Big[mR^2 \cdot\dfrac{v^2}{R^2} \Big]\)
"R²'s" cancel, we are left with:
\(\Longrightarrow mgh+\dfrac{1}{2} mv^2+\dfrac{1}{5} \Big[mR^2\Big]\Big[\dfrac{v^2}{R^2} \Big]\\\\\\\\\Longrightarrow mgh+\dfrac{1}{2} mv^2+\dfrac{1}{5}mv^2\)
We have like terms, combine them.
\(\Longrightarrow mgh+\dfrac{1}{2} mv^2+\dfrac{1}{5} \Big[mR^2\Big]\Big[\dfrac{v^2}{R^2} \Big]\\\\\\\\\Longrightarrow mgh+\dfrac{7}{10} mv^2\)
Each term has an "m" in common, factor it out.
\(\Longrightarrow m(gh+\dfrac{7}{10}v^2)\)
Now we have the following equation:
\(\Longrightarrow m(gh+\dfrac{7}{10}v^2)=\dfrac12mv_{_{0}}^2+\dfrac12\Big[\dfrac25mR^2\Big]\Big[\dfrac{v_{_{0}}}{R}\Big]^2\)
\(\hrulefill\)
Simplifying the right-hand side of the equation:
\(\Longrightarrow \dfrac12mv_{_{0}}^2+\dfrac12\cdot\dfrac25\Big[mR^2\Big]\Big[\dfrac{v_{_{0}}}{R}\Big]^2\\\\\\\\\Longrightarrow \dfrac12mv_{_{0}}^2+\dfrac15\Big[mR^2\Big]\Big[\dfrac{v_{_{0}}}{R}\Big]^2\\\\\\\\\Longrightarrow \dfrac12mv_{_{0}}^2+\dfrac15\Big[mR^2\Big]\Big[\dfrac{v_{_{0}}^2}{R^2}\Big]\\\\\\\\\Longrightarrow \dfrac12mv_{_{0}}^2+\dfrac15\Big[mR^2\cdot\dfrac{v_{_{0}}^2}{R^2}\Big]\\\\\\\\\Longrightarrow \dfrac12mv_{_{0}}^2+\dfrac15mv_{_{0}}^2\Big\\\\\\\\\)
\(\Longrightarrow \dfrac{7}{10}mv_{_{0}}^2\)
Now we have the equation:
\(\Longrightarrow m(gh+\dfrac{7}{10}v^2)=\dfrac{7}{10}mv_{_{0}}^2\)
\(\hrulefill\)
Now solving the equation for the variable "v":
\(m(gh+\dfrac{7}{10}v^2)=\dfrac{7}{10}mv_{_{0}}^2\)
Dividing each side by "m," this will cancel the "m" variable on each side.
\(\Longrightarrow gh+\dfrac{7}{10}v^2=\dfrac{7}{10}v_{_{0}}^2\)
Subtract the term "gh" from either side of the equation.
\(\Longrightarrow \dfrac{7}{10}v^2=\dfrac{7}{10}v_{_{0}}^2-gh\)
Multiply each side of the equation by "10/7."
\(\Longrightarrow v^2=\dfrac{10}{7}\cdot\dfrac{7}{10}v_{_{0}}^2-\dfrac{10}{7}gh\\\\\\\\\Longrightarrow v^2=v_{_{0}}^2-\dfrac{10}{7}gh\)
Now squaring both sides.
\(\Longrightarrow \boxed{\boxed{v=\sqrt{v_{_{0}}^2-\dfrac{10}{7}gh}}}\)
Thus, the simplified equation above matches the simplified equation that was given.
Assuming this rate to be constant how many years will pass before the radius of the Moon's orbit increases by 3.6 x 10^6 m
Answers
The number of years that will pass before the radius of the Moon's orbit increases by 3.6 x 10^6 m will be 90000000 years.
How to compute the value?From the information given, the orbit of the moon is increasing in radius at approximately 4.0cm/yr.
Therefore, we will convey the centimeters to meter. This will be 4cm will be:
= 4/100 = 0.04m/yr.
Time = Distance / Speed
Time = 3.6 x 10^6/0.04
Time = 90000000 years.
Learn more about moon on:
brainly.com/question/13262798
#SPJ1
Complete question:
Tidal friction is slowing the rotation of the Earth. As a result, the orbit of the moon is increasing in radius at approximately 4.0cm/y. Assuming this rate to be constant how many years will pass before the radius of the Moon's orbit increases by 3.6 x 10^6
A ball is thrown straight up in the air at an initial speed of 30 m/s. At the same time the ball is thrown, a person standing 70 m away begins to run toward the spot where the ball will land.How fast will the person have to run to catch the ball just before it hits the ground?Vperson= m/s
Answers
Answer:
Explanation:
Here's what we know and in which dimension:
y dimension:
\(v_0=30\) m/s
v = 0 (I'll get to that injust a second)
a = -9.8 m/s/s
The final velocity of 0 is important because that's the velocity of the ball right at the very top of its travels. If we knew how long it takes to get to that max height, we can also use that to find out how long it will take to hit the ground. Therefore, we will find the time it takes to reach its max height and pick up with the investigation of what this means after.
x dimension:
Δx = 70 m
v = ??
Velocity is our unknown.
Solving for the time in the y dimension:
\(v=v_0+at\) and filling in:
0 = 30 + (-9.8)t and
-30 = -9.8t so
t = 3.1 seconds
We know it takes 3.1 seconds to get to its max height. In order to determine how long it will take to hit the ground, just double the time. Therefore, it will take 6.2 seconds for the ball to come back to the ground, which is where the persom trying to catch the ball comes in. We will use that time in our x dimension now.
In the x dimension, the equation we need is just a glorified d = rt equation since the acceleration in this dimension is 0.
Δx = vt and
70 = v(6.2) so
v = 11.3 m/s
A force that is between any two objects that have net charge
Answers
Answer:
fnet =fa +fg
this is the formula that you apply when calculating a net force between 2 objects
A 75-kg trampoline artist jumps upward from the top of a platform with a vertical speed of 6.0 m/s.
Part A: How fast is he going as he lands on the trampoline, 2.0 m below? (Figure 1)
Express your answer with the appropriate units.
Part B: If the trampoline behaves like a spring of spring constant 6.7×104N/m, how far does he depress it?
Express your answer with the appropriate units.

Answers
Answer:
Explanation:
Part A:
Using conservation of energy, we can find the speed of the trampoline artist just before he lands on the trampoline. At the top of the platform, he has gravitational potential energy equal to mgh, where m is his mass, g is the acceleration due to gravity, and h is the height of the platform. At the bottom of his jump, he has kinetic energy equal to (1/2)mv^2, where v is his speed just before he lands on the trampoline. We can equate these two energies and solve for v:
mgh = (1/2)mv^2
v = sqrt(2gh)
where h = 2.0 m and g = 9.81 m/s^2. Plugging in the values, we get:
v = sqrt(2(9.81 m/s^2)(2.0 m)) = 6.26 m/s
Therefore, the trampoline artist is going 6.26 m/s as he lands on the trampoline.
Part B:
The force exerted by the trampoline on the artist is equal to the weight of the artist, which is mg, where g is the acceleration due to gravity. This force causes the trampoline to compress a distance d, which we want to find. From Hooke's law, we know that the force exerted by a spring is equal to its spring constant times its deformation from its equilibrium length. Therefore:
mg = kd
where k is the spring constant of the trampoline. Solving for d, we get:
d = (mg)/k
where m = 75 kg, g = 9.81 m/s^2, and k = 6.7×10^4 N/m. Plugging in the values, we get:
d = (75 kg)(9.81 m/s^2)/(6.7×10^4 N/m) = 0.109 m
Therefore, the trampoline depresses 0.109 m when the artist lands on it.
What is the minimum amount ( in kg) of liquid water at 26 degrees that would be required to completely melt 41 grams of ice? The specific heat capacity of liquid water is 4180 J/kg/°C and the specific heat of fusion of ice is 3.33×105 J/kg.
Answers
Approximately 0.123 kg of liquid water at 26 degrees Celsius would be needed to melt 41 grams of ice.
To calculate the minimum amount of liquid water required to melt 41 grams of ice at 0°C, we need to consider the energy required for the phase change from solid to liquid, which is known as the specific heat of fusion of ice.
The energy required to melt 1 kg of ice is 3.33×105 J/kg.
Therefore, the energy required to melt 41 grams of ice is (3.33×105 J/kg) × (41/1000) kg = 13653 J.
To calculate the amount of liquid water required, we use the specific heat capacity of water, which is 4180 J/kg/°C.
Assuming the initial temperature of water is 26°C, the amount of water needed can be calculated as (13653 J) ÷ (4180 J/kg/°C) ÷ (26°C) = 0.123 kg or approximately 123 ml of water.
For more such questions on Celsius, click on:
https://brainly.com/question/30403835
#SPJ11
10) A ball falls from the top of the Empire State Building, through the air (air friction is present), to the ground below. How does itskinetic energy (K) just before striking the ground compare to its potential energy (U) at the top of the building?Select one:A. It is impossible to tell.B. Kis equal to U.2C. Kis greater than U.D. K is less than U.
Answers
kinetic energy = 1/2* m* v^2
Potential energy = m*g*h
Where:
m= mass
g= acceleration due to gravity
h= height
v= velocity
on the top of the building:
K = max ( max height)
U= 0 (no velocity)
Before striking the ground:
k= gets lower ( less h)
U= higher ( it has velocity)
Answer
D. K is less than U.
Rhea is driving north in a straight line. After driving for 2.4 kilometers, she turns west, and drives for 3.1 km. At the end of her drive, what is the magnitude of her displacement vector? To find the magnitude of a resultant vector, use the Pythagorean theorem: a² + b² = c² A) 3.9 km B) 5.5 km (this one is incorrect) C) 2.8 km D) 2.3 km
Answers
Option A) 3.9 km is the correct answer. the magnitude of Rhea's displacement vector is approximately 3.92 km.
In order to find out the magnitude of Rhea's displacement vector, we have to add up all of the displacement vectors.
Then we can use the Pythagorean theorem to calculate the magnitude of the resultant vector.
Since Rhea is first driving north for 2.4 km and then west for 3.1 km, we can represent her displacement vectors as follows: Δx = 0 km and Δy = 2.4 km for the first vector, and Δx = -3.1 km and Δy = 0 km for the second vector.
We can then add these vectors together by adding their components: Δx = 0 km + (-3.1 km) = -3.1 km and Δy = 2.4 km + 0 km = 2.4 km.
This gives us a resultant vector of -3.1 km east and 2.4 km north.
Using the Pythagorean theorem, we can find the magnitude of this vector: \(\sqrt{(\(-3.1 km)^{2} + (2.4 km)^{2} ) } = \sqrt{(9.61 + 5.76) km^{2} } = \sqrt{15.37 km^{2} } \approx 3.92 km.\)
Therefore, the magnitude of Rhea's displacement vector is approximately 3.92 km.
Therefore, option A) 3.9 km is the correct answer.
For more questions on displacement vector
https://brainly.com/question/28952425
match the words in the left-hand column to the appropriate blank in the sentences in the right-hand column. use each word only once. a blankpredicts that the strong, weak, and electromagnetic forces should become indistinguishable at high temperatures
1. A grand unified theory predicts that the strong, weak, and electromagnetic forces should become indistinguishable at high temperatures
2. The electroweak force is a single force that unifies the electromagnetic and weak forces.
3. Inflation was a dramatic expansion of the universe thought to have occurred when the universe was only a tiny fraction of a second old.
4. Olbers' paradox forces us to think about why the sky is dark at night.
5. Observations of the cosmic microwave background provide a way to test our theory of the Big Bang.
6. When a particle of ordinary matter meets its precise opposite particle of antimatter, the result is annihilation with complete conversion of mass into energy.
Answers
The correct matches for the given words are:
1. grand unified theory - predicts the strong, weak, and electromagnetic forces
2.electroweak force
3. Inflation
4. Olbers' paradox
5. cosmic microwave background
6. annihilation
What is electromagnetic force ?Physical interactions between electrically charged particles are known as the electromagnetic force. It is the result of the interaction of all magnetic and electrical forces and operates between charged particles.
Both visible light and radiation in other wavebands that the human eye cannot see are produced by the electromagnetic field.
A faint glow of light known as the Cosmic Microwave Background radiation, or CMB for short, permeates the entire cosmos and falls on Earth with a remarkably consistent intensity from all directions.
To know more about electromagnetic force you may visit the link:
https://brainly.com/question/13191643
#SPJ4
Only need question number 3

Answers
The magnetic field at a point due to wires with distance r = C cm and carrying the current I is 2 mA is 0.29 T.
The magnetic field is produced over the magnet or current-carrying conductor. The Biot-Sarvat law is defined as the magnetic field produced due to the current-carrying conductor. The magnetic field is the vector quantity and the unit of the magnetic field is Tesla. It is the vector quantity.
Magnetic field, B = μ₀/2π (I/R), where μ₀ is the permeability of the magnetic field, I is current, and R is the distance between two points.
B₁= μ₀/2π (I/R)
= (1.26×10⁻⁶)×2×10⁻³/(2π×1.35m)
= 0.29T
B₂ = 0.29T
The net magnetic field is B=B₁+B₂=0.58T.
Thus, the magnetic field is 0.29T. The left wire carries the current outward direction and the right wire carried the current inward direction and hence the direction magnetic field given by the right-hand thumb rule is inside.
B) By using the equation, F=q(v×B), where q is the charge, v is the velocity and B is the magnetic field. Path b is followed by a neutron as it is not deflected by a Magnetic field. The path a is the upward path followed by a negatively charged particle(electron) and Path C is the downward path followed by a positively charged particle(proton).
C) The circular conductor undergoes thermal expansion while it is a uniform magnetic field the direction of the current is a clockwise direction given by the Right-hand thumb rule.
To learn more about Bior-Sarvat law:
https://brainly.com/question/1120482
#SPJ1
If each wafer can hold 400 chips, what is the maximum number of chips that can be produced from one entire cylinder?
Answers
The maximum number of chips is 33,333
What is a chip?
A chip is a tiny but complex modules that store computer memory or provide logic circuitry for microprocessors.
We need to find the number of wafers that can be cut from a single crystal.
The crystal is 25cm and each wafer is 0.3mm. We perform division to get the number of wafers per crystal after getting everything into the same units. 25cm=250mm.
250mm/0.3mm=833.3333 wafers.
Each wafer yields 400 chips so we multiply 400 chips per wafer by 833.33 wafers to get 33,333 chips.
Learn more about chips at: https://brainly.com/question/22738250
#SPJ1
A light-year (ly) is the distance light travels in one year (at speed of 2.998 × 108 m/s). An astronomical unit (AU) is the average distance from the Sun to Earth, 1.50 × 108 km. 1 year = 3.156 × 107 s.
A) How many meters are there in 1.90 ly?
B) How many AU are there in 1.90 ly?
Answers
Answer:.47 x 10 *15* meters in 1.00 ly
there are 6.31 x 10 *4* au on 1.00 ly
Explanation:
Which trait do you think is most important for a boss or supervisor to have?
Answers
Answer:
A high EQ (emotional intelligence)
In today's transitioning workplace, having a high EQ is the most important trait of a good boss. Bosses must be able to discern between their own personal beliefs and the thoughts and beliefs of others, and other generations (boomers, Gen X, xennials, millennials and now Gen Z).
Explanation:
hope it helps you
How do you calculate the maximum angle at which an object will not slip on an incline? I know that it's arctan(μ) but why? Where does that come from? Thank you in advance!
Answers
The maximum angle at which an object will not slip on an incline can be calculated using the coefficient of friction (μ).
Balance of forces on an inclineWhen an object is on an inclined plane, there are two main forces acting on it: the gravitational force pulling it downward (mg) and the normal force (N) exerted by the inclined plane perpendicular to its surface. Additionally, there is a frictional force (F) acting parallel to the surface of the incline.
To prevent slipping, the frictional force must be equal to or greater than the force component pulling the object down the incline. This force component is given by the equation F = mg sin(θ), where θ is the angle of inclination.
The maximum frictional force that can be exerted between two surfaces is given by the equation F = μN, where μ is the coefficient of friction.
For an object not to slip, the maximum frictional force (F) must be equal to or greater than the force component pulling the object down the incline (mg sin(θ)). Therefore, we have:
F ≥ mg sin(θ)
Substituting F = μN, we get:
μN ≥ mg sin(θ)
Since N = mg cos(θ) (the normal force is equal to the component of the gravitational force perpendicular to the incline):
μmg cos(θ) ≥ mg sin(θ)
μ cos(θ) ≥ sin(θ)
Now, divide both sides of the equation by cos(θ):
μ ≥ tan(θ)
Taking the inverse tangent (arctan) of both sides, we get:
θ ≤ arctan(μ)
Therefore, the maximum angle at which an object will not slip on an incline is given by θ = arctan(μ).
More on inclined planes can be found here: https://brainly.com/question/29360090
#SPJ1
a=5i+4j-6k ,b=-2i+2j+3k ,c=4i+3j+2k. find the vector perpendicular to a and c
Answers
Answer:
Explanation:
You can use the cross product. Let the vector that perpendicular to a and c is \(\vec{d}\), so:
\(\vec{d}=\vec{a}\times\vec{c}=\left|\left[\begin{array}{ccc}\hat{i}&\hat{j}&\hat{k}\\5&4&-6\\4&3&2\end{array}\right] \right|=(8+18)\hat{i}-\hat{j}(10+24)+\hat{k}(15-16)=26\hat{i}-34\hat{j}-\hat{k}\)
To check that c is perpendicular with a and b, do the dot product between c and a and also c and b and if the result is zero, you're true.
\(\vec{d}.\vec{a}=(26*5)-(34*4)+(6)=0\) (c perpendicular to a)
\(\vec{d}.\vec{c}=(4*26)-(34*3)-(2*1)=0\) (d perpendicular to c)
What is the energy transfer from one object to another object
Answers
Answer:
Kinetic energy
Explanation:
"Kinetic energy is the energy an object has because of its motion."
A pulse of sound takes 1 second to travel about 25 feet to the seafloor
100
and back. A ship stops in an area where the seafloor extends to the bottom
of the Sunlight Zone. At this spot an echosounder gives a pulse of sound
that takes 26 second to travel to the seafloor and back. How deep is the
100
ocean at the bottom of the Sunlight Zone?
HELP!!! I’m stumped!! Get max points ( if it lets me! )
Answers
Answer: The depth of the ocean is 650 feets at the bottom of the sunlight zone.
The distance travelled by echo sound is given by the formula -
Speed = 2×distance/time
So, calculating the speed of sound from the formula using distance and time
Speed = 2×25/(1/100)
Speed = 50×1000
Speed of sound = 5000 feet/second
Now, calculating the distance or depth of ocean at the bottom of the sunlight zone -
Distance = (speed×time)/2
Distance = (5000×26/100)/2
Distance = 1300/2
Distance = 650 feets
Hence, the depth of ocean is 650 feets.
Learn more about echo -
brainly.com/question/19579065
Answer:
We can start by using the formula:
distance = speed x time
where distance is twice the depth of the ocean at the bottom of the Sunlight Zone (since the pulse travels down to the seafloor and then back up), speed is the speed of sound in water, and time is the round-trip time of the pulse.
The speed of sound in water is approximately 1,500 meters per second (or 4,921 feet per second).
Converting the round-trip time to seconds, we have:
26 seconds - 1 second = 25 seconds
Substituting the values into the formula:
2 x depth = 4,921 feet/second x 25 seconds
2 x depth = 123,025 feet
depth = 61,512.5 feet
Therefore, the ocean at the bottom of the Sunlight Zone is about 61,512.5 feet deep.
3) A 60. kg person is in an elevator. The elevator starts from rest and then accelerates upwards at 2.0 m/s^2 for 4.0 seconds. Calculate the work done by the normal force on the person. *
Answers
Answer:
WD = 960 J
Explanation:
WD = work done (J)
F = force (N)
s = displacement (m)
m = mass (kg) = 60
a = acceleration (m/s²) = 2
t = time (s) = 4
u = initial velocity (m/s) = 0
The formulas or equations that are relevant ate:
WD = F × s
F = m × a
s = u + at
We want to find WD, so we need to now the force and the displacement (or distance);
We calculate force, in Newtons, with the formula F = ma:
F = 60 × 2
F = 120 N
We also need displacement, which get with the formula s = u + at:
s = 0 + 2(4)
s = 8 m
Now we have F and s, we can calculate WD:
WD = 120 × 8
WD = 960 J
Methodology:
Starting with what you want to find, in this case WD, list the formula/s you could use;
Then, identify the information you need for the formula and whether or not you are given that information;
Next, list the formulas for the information you don't have and once again, identify whether the information you are given is sufficient to use those formulas;
Once you can calculate all necessary information, then proceed to calculate the values and finally, the answer;
I suggest also keeping a list of all the variables as I've done at the top of my working so it is clear for you to see and use.
A frog is riding on the top of a cylindrical piece of wood floating in still water. Half of the wood, with a diameter of 4 cm and length 20 cm, is immersed in water. The density of water is 1 gm/cc. a) What is the mass of the wood along with the frog? b) After the frog slowly goes into the water only one third of the wood remains immersed in water. Calculate the mass of the frog. c) Calculate x, the distance between the water level and the center of the circular end of the wooden piece. d) Briefly describe the motion of the wood after the instance the frog moves into the water. Give a rough sketch of x as a function of time.
Answers
The total mass of the wood along with the frog is 120π gm.
The mass of the frog is (160/3)π gm.
How to calculate the MassThe volume of the wood that is immersed in water is given by the volume of a cylinder with a radius of 2 cm and a height of 10 cm, which is V1 = π(2cm)²(10cm) = 40π cm³. The mass of the water displaced by this volume of wood is m1 = V1ρ = 40π gm. The mass of the remaining part of the wood above water is m2 = ρV2 = ρ(π(2cm)²(10cm)) = 80π gm.
mTherefore, the total mass of the wood along with the frog is m1 + m2 = 120π gm.
b) After the frog goes into the water, the volume of the wood that is immersed decreases to V3 = (1/3)π(2cm)^2(20cm) = (80/3)π cm^3. The mass of the water displaced by this volume of wood is m3 = V3ρ = (80/3)π gm. Therefore, the mass of the frog is (m1 + m2) - m3 = (120π - (80/3)π) gm = (240/3)π - (80/3)π = (160/3)π gm.
Learn more about mass on;
https://brainly.com/question/28021242
#SPJ1
It is a “new moon” (the Moon is totally dark in the sky). Using the masses of the Earth, Sun, and Moon and the average distances between the Earth-Moon and Earth-Sun, find the net gravitational force on the Earth from the Sun and the Moon combined.
Find also distance when it is full moon
Answers
It is a “new moon” (the Moon is totally dark in the sky). The gravitational force between the Earth and the Moon is:
2.9 x 10^20 N3.5 x 10^22 N3.5 x 10^22 NWhat is gravitational force?Generally, The gravitational force between two objects is given by the equation:
force = G * (mass1 * mass2) / distance^2
Where G is the gravitational constant (6.67 x 10^-11 N*(m/kg)^2), mass1 and mass2 are the masses of the two objects, and distance is the distance between the two objects.
The mass of the Earth is 5.972 x 10^24 kg, the mass of the Moon is 7.347 x 10^22 kg, and the mass of the Sun is 1.989 x 10^30 kg. The average distance between the Earth and the Moon is 384,400 km, and the average distance between the Earth and the Sun is 149.6 million km.
The gravitational force between the Earth and the Moon is:
force = (G * (mass of Earth) * (mass of Moon)) / (distance between Earth and Moon)^2 force
= (6.67 x 10^-11 N*(m/kg)^2) * (5.972 x 10^24 kg) * (7.347 x 10^22 kg) / (384400 x 10^3 m)^2 force
= 2.9 x 10^20 N
The gravitational force between the Earth and the Sun is:
force = (G * (mass of Earth) * (mass of Sun)) / (distance between Earth and Sun)^2 force
= (6.67 x 10^-11 N*(m/kg)^2) * (5.972 x 10^24 kg) * (1.989 x 10^30 kg) / (149.6 x 10^9 m)^2 force
= 3.5 x 10^22 N
To find the net gravitational force on the Earth from the Sun and Moon combined, we add the two forces we found above.
Net force = 2.9 x 10^20 N + 3.5 x 10^22 N
= 3.5 x 10^22 N
When it is a Full Moon the distance is the same 384,400 km
Read more about gravitational force
https://brainly.com/question/12528243
#SPJ1