Plsssss help!!! Brainliest....

Answer:

15 bags

Step-by-step explanation:

3(0) + 7y=105

7y=105

y=15

The graph of the exponential function is in the image at the end.

Here we want to graph the function:

f(x) = 2*2ˣ

To do so, we need to evaluate the function in some values, and then we can find some points in the graph, and then we can use these points to sketch the graph.

When x = 0 we get.

f(x) = 2*2⁰ = 2 ----> (0, 2)

when  x = -1

f(-1) = 2*2⁻¹ = 1 ---> (-1, 1)

When x = 1

f(1) = 2*2¹ = 4 ----> (1, 4)

And so on, when you have enough points, you can graph them and connect them with a curve, the graph you will get is something like the one below.

Learn more about exponential function at:

https://brainly.com/question/2456547

#SPJ1

The function y(t) = 1/cos(t) is a solution to the differential equation d2y/dt2 = 2y3 - y if it satisfies the equation when substituted into it. To verify this, we can substitute the function into the equation and simplify.

First, let's find the first and second derivatives of the function:
dy/dt = (sin(t))/(cos^2(t))
d2y/dt2 = (2sin^2(t))/(cos^3(t)) - (1/cos^3(t))

Now, let's substitute these derivatives and the original function into the differential equation:
(2sin^2(t))/(cos^3(t)) - (1/cos^3(t)) = 2(1/cos(t))^3 - (1/cos(t))

Simplifying the right side of the equation gives us:
(2sin^2(t))/(cos^3(t)) - (1/cos^3(t)) = (2/cos^3(t)) - (1/cos(t))

Combining like terms on the right side gives us:
(2sin^2(t))/(cos^3(t)) - (1/cos^3(t)) = (2 - cos^2(t))/(cos^3(t))

Since sin^2(t) + cos^2(t) = 1, we can substitute 1 - cos^2(t) for sin^2(t) to get:
(2(1 - cos^2(t)))/(cos^3(t)) - (1/cos^3(t)) = (2 - cos^2(t))/(cos^3(t))

Simplifying the left side gives us:
(2 - 2cos^2(t))/(cos^3(t)) - (1/cos^3(t)) = (2 - cos^2(t))/(cos^3(t))

Combining like terms on the left side gives us:
(1 - cos^2(t))/(cos^3(t)) = (2 - cos^2(t))/(cos^3(t))

Since both sides of the equation are equal, we can conclude that the function y(t) = 1/cos(t) is a solution to the differential equation d2y/dt2 = 2y3 - y.

To know more about differential equation refer here:

https://brainly.com/question/1164377#

#SPJ11

Answer:

z= 13

x= 36

y= 18

Step-by-step explanation:

Solving for z.

We know that 108 degrees and (8z+4) are alternate exterior angles, so they are equal to each other.

We can set both of those angles equal to each other, and solve for our missing side, z.

108= 8z+4

104=8z

z= 13

Solving for x.

We know that 108 degrees and (3x) are alternate interior angles, so they would equal each other.

We can set both of these angles equal to each other, and solve for our missing side, x.

3x=108

x= 36

Solve for y.

We know that (4y) and (3x) are same side interior angles, so they would make 180 degrees. We know that (3x) would equal 108.

4y+108=180

4y= 72

y= 18

The first derivatives for the given functions are:

For \(y = 3x^2 + 5x + 10,\) the first derivative is dy/dx = 6x + 5.

For  \(y = 100200x + 7x,\) the first derivative is dy/dx = 100207.

For \(y = ln(9x^4),\) the first derivative is dy/dx = 4/x.

To find the first derivative for each of the given functions, we'll use the power rule, constant rule, and chain rule as needed.

For the function\(y = 3x^2 + 5x + 10:\)

Taking the derivative term by term:

\(d/dx (3x^2) = 6x\)

d/dx (5x) = 5

d/dx (10) = 0

Therefore, the first derivative is:

dy/dx = 6x + 5

For the function y = 100200x + 7x:

Taking the derivative term by term:

d/dx (100200x) = 100200

d/dx (7x) = 7

Therefore, the first derivative is:

dy/dx = 100200 + 7 = 100207

For the function \(y = ln(9x^4):\)

Using the chain rule, the derivative of ln(u) is du/dx divided by u:

dy/dx = (1/u) \(\times\) du/dx

Let's differentiate the function using the chain rule:

\(u = 9x^4\)

\(du/dx = d/dx (9x^4) = 36x^3\)

Now, substitute the values back into the derivative formula:

\(dy/dx = (1/u) \times du/dx = (1/(9x^4)) \times (36x^3) = 36x^3 / (9x^4) = 4/x\)

Therefore, the first derivative is:

dy/dx = 4/x

To summarize:

For \(y = 3x^2 + 5x + 10,\) the first derivative is dy/dx = 6x + 5.

For y = 100200x + 7x, the first derivative is dy/dx = 100207.

For\(y = ln(9x^4),\) the first derivative is dy/dx = 4/x.

For similar question on derivatives.

https://brainly.com/question/31399608

#SPJ8

The combinatA combinatorial proof for the identity Σ(n-m+r choose r) (r=0 to m) = (n+1 choose m+1) is as follows:

Consider a set of (n+1) distinct objects labeled from 0 to n. We want to count the number of ways to choose a subset of (m+1) objects from this set.

On the left-hand side of the identity, we can break down the sum as follows:
Σ(n-m+r choose r) (r=0 to m)

Each term in the sum represents choosing a different number of objects from the first (n-m) objects. The term (n-m+r choose r) represents choosing r objects from the first (n-m) objects, where r ranges from 0 to m.

Now, let's consider the right-hand side of the identity, (n+1 choose m+1). This represents choosing (m+1) objects from the set of (n+1) objects.

We can interpret the left-hand side as counting the number of ways to choose a subset of (m+1) objects from a set of (n+1) objects using combinatorial reasoning. The right-hand side represents the same count directly by using the binomial coefficient. Therefore, both sides of the identity represent the same quantity, and the combinatorial proof verifies the given identity.

To know more about  combinatorial proof,visit:
https://brainly.com/question/32415345
#SPJ11

Answer:

40% of $800 = 320

25% of $600 = 150

The time which both of take to deliver 51 papers is 3.4hours.

Since, we have time which Maria and Charlie are taking to deliver 45 papers.

Whenever some relation is given for any object with time and it is asking same relation at any other time, we need to use unitary methods.

So, we use unitary method.

45 papers are delivered in =3 hours

1 paper is delivered in =(3/45)hours

Therefore, 51 papers are delivered in :

=(3/45)×51hours

=(51/15)hours

=17/5hours

=3.4hours

Hence, 3.4 hours will be taken by both to deliver 51 papers.

To know more about unitary methods, visit here:

https://brainly.com/question/28276953

#SPJ4

Answer:

Correct answer is C- Money market accounts have higher interest rates than regular savings accounts but with more restrictions

Step-by-step explanation:

took the quiz

Answer:

4.3cm

Step-by-step explanation:

the radius of the hemisphere can be determined its volume

volume of a hemisphere = (2/3) x (n) x (r^3)

n = 22/7

r = radius

(2/3) x (22/7) x( r^3) = 165 cm^3

44/21 x r^3 = 165

divide both sides of the equation by 21/44

165 x 21/44

r^3 = 78.75

find the cube root

r = 4.2863 cm

the tenth is the first number after the decimal place. To convert to the nearest tenth, look at the number after the tenth (the hundredth). If the number is greater or equal to 5, add 1 to the tenth figure. If this is not the case, add zero

the 100th terms, 8 is greater than 6, so add 1 to 2. this give 4.3cm

Answer:

your answer is up there

Step-by-step explanation:

Sorry for not being some help i really am Red Riot out

The roots of the quadratic equation 0 = 2x² + 12x-14 is (C) x=-7 and x=1.

Any equation in algebra that can be written in the standard form where x stands for an unknown value and a, b, and c stand for known values is said to be a quadratic equation.

In general, it is assumed that a > 0; equations with a = 0 are regarded as degenerate since they become linear or even simpler.

So, the roots of 0 = 2x² + 12x-14 are:

2x² + 12x-14  = 0

2x² + 14x - 2x -14

2x(x + 7) - 2(x + 7)

(2x - 2) (x + 7)

Now, use the zero product property as follows:

2x - 2 = 0

2x = 2

x = 2/2

x = 1

And

x + 7 = 0

x = -7

Therefore, the roots of the quadratic equation 0 = 2x² + 12x-14 is (C) x = -7 and x = 1.

Know more about a quadratic equation here:

https://brainly.com/question/1214333

#SPJ1

Correct question:

What are the roots of the quadratic equation 0 = 2x² + 12x-14?

a. 1,6, -7

b. 2,12,-14

c. -7,1

d. -1,7

Answer:

10 dimes and 6 quarters.

Step-by-step explanation:

2.50-25-25=2.00-10 dimes = 1.00-4 0.25=0

so

10 dimes and 6 quarters.

Answer:

10 Dimes and 6 Quarters.

Step-by-step explanation:

Important info:

16 Coins

Total = $2.50

Note:

Dimes = 0.10 Cents

Quarters = 0.25 Cents

Question to answer:

How many of each type of coin does she have?

Solution:

10 Dimes = $1.00

6 Quarters = $1.50

$1.00+$1.50 = $2.50

Therefore 10 Dimes and 6 Quarters = $2.50 and = 16 Coin.

Answer:

C. 30

Step-by-step explanation:

1 times 1 is 1

5 times 5 is 25

6 times 6 is 36

Answer:

The answer is 30

Step-by-step explanation:

Answer:

Step-by-step explanation:

Use the equation x = -b/2a => x = -12/6 = -2.

For the statement to happen, the number should be 2.

An algebraic expression is is defined as the combination of numbers and variables in solving a particular mathematical question. Variable, usually letters, are used to denote the unknown quantity.

Let x = number

Based on the information given, add the number to the numerator of 11/35 and add twice the number to the denominator of 11/35, and the result should be equal to 1/3.

Hence, (11 + x) / (35 + 2x) = 1/3.

Simplify and solve for the value of x.

3(11 + x) = (35 + 2x)

33 + 3x = 35 + 2x

3x - 2x = 35 - 33

x = 2

number = 2

Learn more about algebraic expression here: https://brainly.com/question/3927786

#SPJ4

Answer:

It will be 40

Step-by-step explanation:

Hope this helped have an amazing day!

The given statement is,

→ if u have 10 and add 20 and add 10.

In mathematical expression,

→ (10 + 20) + 10

→ 30 + 10

→ 40 is the answer.

The value of angle S is 53°

Exterior angle theorem states that the measure of an exterior angle of a triangle is equal to the sum of two remote interior angles.

With this theorem we can say that

7x+2 = 4x+13+19

collecting like terms

7x -4x = 13+19-2

3x = 30

divide both sides by 3

x = 30/3

x = 10

Since x = 10

angle S = 4x+13

angle S = 4(10) +13

= 40+13

= 53°

Therefore the measure of angle S is 53°

learn more about exterior angle theorem from

https://brainly.com/question/17307144

#SPJ1

Answer:

p= 4s

40 m

Step-by-step explanation:

Answer:

You would multiply 10 by 4 or add 10 4 times. A square has 4 sides and if each side is 10 meters, the answer would be

40 meters

:)

Answer:

480 cm2

Step-by-step explanation:

8 isosceles triangles of sides 13cm,13cm,10cm

By Heron's Formula,

Area =

s(s−a)(s−b)(s−c)

Where s=

2

a+b+c

s=

2

13+13+10

=18

Area of triangle =

18×(18−13)×(18−13)×(18−10)

(Heron's formula)

Area of triangle =

18×5×5×8

=5

144

Area of triangle =60cm

2

Area of cloth made of 8 triangles =60×8

=480cm2

Using the dual simplex method to find a solution to the linear programming problem formed by adding the constraint 3xi 5x3> 15 to the problem. The final solution is:
xi = 20
x2 = 0
x3 = 15
x4 = 0
x5 = 40

Adding the constraint 3xi + 5x3 > 15 does not affect the optimal solution, as none of the variables involved in the new constraint are in the basis. Therefore, the final solution remains the same.

To use the dual simplex method to find a solution to the linear programming problem formed by adding the constraint 3xi + 5x3 > 15 to the problem in example 2, we need to follow these steps:

1. Rewrite the problem in standard form by adding slack variables:
Maximize 4xi + 3x2 + 5x3
Subject to:
2xi + 3x2 + 4x3 + x4 = 60
3xi + 2x2 + x3 + x5 = 40
xi, x2, x3, x4, x5 >= 0

2. Calculate the initial feasible solution by setting all slack variables to 0:
xi = 0
x2 = 0
x3 = 0
x4 = 60
x5 = 40

3. Calculate the reduced costs of the variables:
c1 = 4 - 2/3x4 - 3/2x5
c2 = 3
c3 = 5 - 2/3x4 - 1/2x5
c4 = -2/3x1 - 1/2x2
c5 = -3/2x1 - 1/2x2

4. Choose the entering variable with the most negative reduced cost. In this case, it is x1.

5. Calculate the minimum ratio test for each constraint to determine the leaving variable:
For the first constraint: x4/2 = 30, x1/2 = 0, so x4 is the leaving variable.
For the second constraint: x5/3 = 40/3, x1/3 = 0, so x5 is the leaving variable.

6. Update the solution by performing the pivot operation:
- Pivot on x1 and x4 in the first constraint: x1 = 20, x4 = 0, x2 = 0, x3 = 15, x5 = 40/3
- Pivot on x1 and x5 in the second constraint: x1 = 0, x4 = 0, x2 = 0, x3 = 15, x5 = 40

7. Repeat steps 3-6 until all reduced costs are non-negative or all minimum ratio tests are negative.

Know more about constraint here:

https://brainly.com/question/30703729

#SPJ11

Answer:

2x - 10y = - 40

Step-by-step explanation:

x - 3y = -14

x - 7y = -26

2x - 10y = - 40

Answer:

54m²

Step-by-step explanation:

Pythagorium theory

15²=12²+x²=> x=square root of 15²-12²

x=square root of 81

x=9

12*9/2=54m²

To solve the given differential equation by the method of undetermined coefficients, first identify the form of the equation: y'' - 5y' + 4y = 8.

This is a second-order linear homogeneous differential equation with constant coefficients. Since the right-hand side is a constant, we guess a particular solution of the form: yp = A, where A is an undetermined coefficient. Now we can find the first and second derivatives: yp' = 0
yp'' = 0

Substitute these values back into the original differential equation: 0 - 5(0) + 4A = 8
This simplifies to: 4A = 8
Now we can solve for the undetermined coefficient: A = 8 / 4
A = 2

So the particular solution is: yp = 2
Now we can find the complementary solution by solving the homogeneous equation: y'' - 5y' + 4y = 0
The characteristic equation is: r^2 - 5r + 4 = 0

Factoring this equation gives: (r - 4)(r - 1) = 0
So the roots are r1 = 4 and r2 = 1. The complementary solution is given by: yc = C1 * e^(4x) + C2 * e^(x)
Finally, the general solution is the sum of the complementary and particular solutions:
y(x) = C1 * e^(4x) + C2 * e^(x) + 2
where C1 and C2 are constants determined by initial conditions (if provided).

To know more about derivative click here

brainly.com/question/29096174

#SPJ11

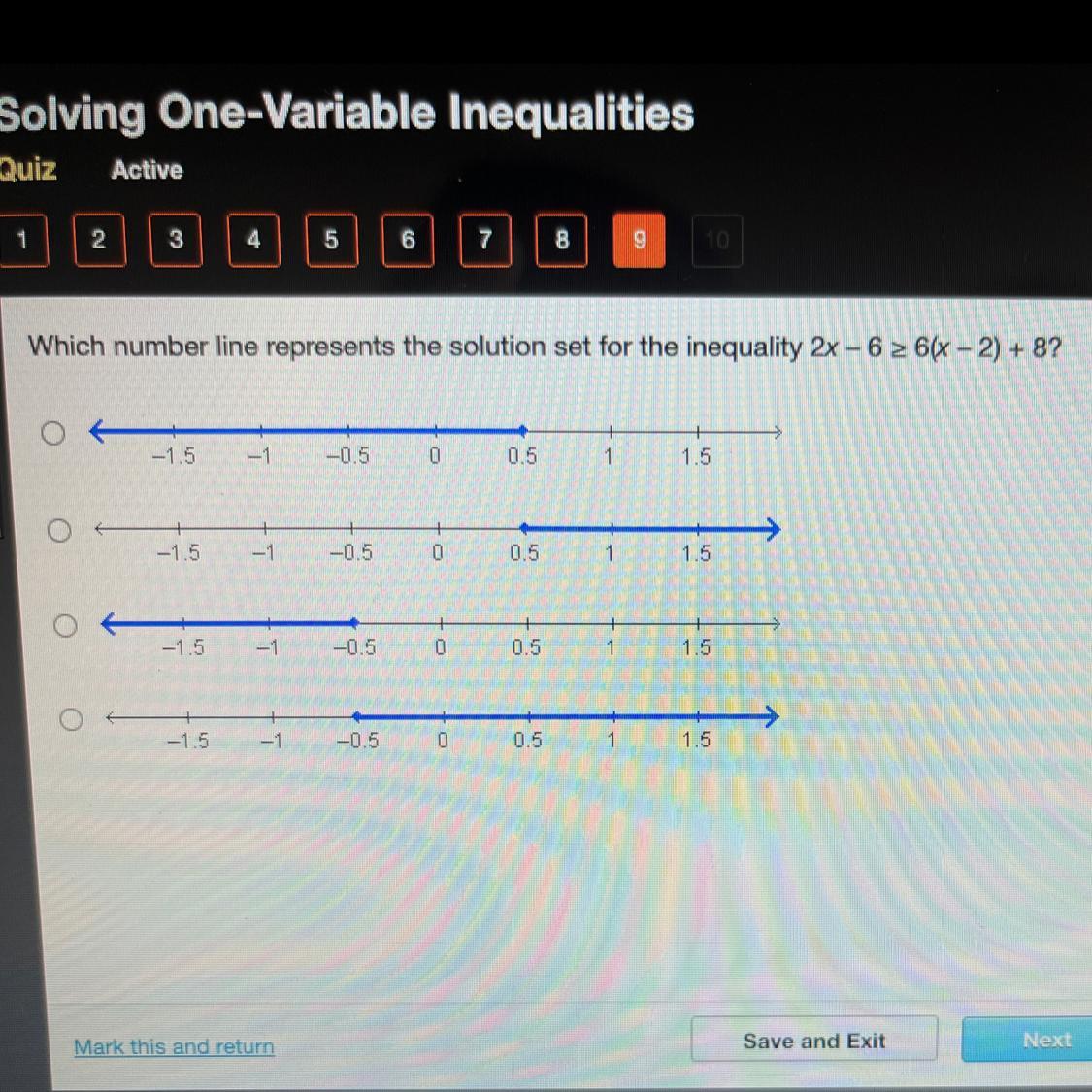
Answer:

Step-by-step explanation:

The answer is C

Answer:  $17.92/sandwich

Step-by-step explanation:

Let S be the price of a sandwich ($/sandwich).

7S is the total cost of the sandwiches.  Add a drink for $2.50 to find the total cost, which we are told comes to $140.50

7S + $2.50 = $140.50

7S = $138

S = $19.7143

It is odd that this includes a fraction of a single penny (0.43 cents).  Something is incorrect in the data given, since this should equal a whole number.  For now, I'll round up to $19.72.  The additional 7*($0.0043) = 4 cents will be treated as a tip.

Answer:

B. 5 2/5

Step-by-step explanation:

Use the long division solution to convert the original fraction  ( 27/ 5 )  to a mixed number. The whole number portion of the mixed number will be the number of times the denominator of the original fraction divides evenly into the numerator of the original fraction ( 5 ) , and the fraction portion of the mixed number will be the remainder of the original fraction division  ( 2 )  over the denominator of the original fraction  ( 5 )

\(\textit{area of a sector of a circle}\\\\ A=\cfrac{\theta \pi r^2}{360}~~ \begin{cases} r=radius\\ \theta =\stackrel{degrees}{angle}\\[-0.5em] \hrulefill\\ r=8\\ \theta =80 \end{cases}\implies \begin{array}{llll} A=\cfrac{(80)\pi (8)^2}{360}\implies A=\cfrac{128\pi }{9} \\\\\\ A\approx 44.68~in^2 \end{array}\)

Answer: 110 yards.

Step-by-step explanation:

According to the cosine formula,

In a triangle, if a and b are two consecutive sides and x is the angle between them, then the measure of the third side (c) is given by:-

\(c=\sqrt{a^2+b^2-2ab\cos x}\)

As per given, a= 70 yards , b= 95 yards , x=  82 degrees

The final side = \(\sqrt{(70)^2+(95)^2-2(70)(95)\cos 82^{\circ}}\)

\(=\sqrt{4900+9025-13300(0.139173)}\\\\=\sqrt{13925-1851} \\\\=\sqrt{12074}\\\\\approx110\text{ yards}\)

I.e. the length of the final side of the plot is 110 yards.