Answers
Answer:
Graph A.
Step-by-step explanation:
Graph A has plotted points that are the exact same as for the equation.
The equation is:
y = x - 1
Meaning:
the slope is +1.
the y-intercept is -1.
Points for the equation:
(0, -1)
(1, 0)
(2, 1)
(3, 2)
(4, 3)
(5, 4)
(6, 5)
(7, 6)
(8, 7)
Points on Graph A:
(1, 2)
(5, 4)
(8, 7)
Therefore, Graph A is your correct option.
Related Questions
A quadratic equation, y = ax^2 - 6x + 10, has exactly one real root. Calculate the value of a.
Answers
Answer:
a = 0.9
Step-by-step explanation:
For the quadratic equation \(\boxed{ax^2 + bx + c = 0}\) to have exactly one real root, the value of its discriminant, \(\boxed{b^2 - 4ac}\), must be zero.
For the given equation:
\(y = ax^2 - 6x + 10\),
• a = a
• b = -6
• c = 10.
Substituting these values into the formula for discriminant, we get:
\((-6)^2 - 4(a)(10) = 0\)
⇒ \(36 - 40a = 0\)
⇒ \(36 = 40a\)
⇒ \(a = \frac{36}{40}\)
⇒ \(a = \bf 0.9\)
Therefore the value of a is 0.9 when the given quadratic has exactly one root.
Determine la ecuación de la recta normal a la curva f(x)=ax(bx+a) en el punto de abscisa x=1. Dar como respuesta el intercepto al Eje Y . Considere el valor de a=7 ,b=10
Answers
Answer:
\(f(x) = ax(bx + a) \\ a = 1 \: b = 10 \: x = 1 \\ f(x) = ax(bx + a) \\ f(1) = 7(1)(10(1) + 7) \\ f(1)= 7(10 + 7) \\ f(1)= 70 + 49 \\ f(1)= 149\)
Which of the following rational functions is graphed below?
A. F(x) =(x-2)/(x+5)
B. F(x) =1/(x-2)(x + 5)
C. F(x) =1/(2x + 5)
D. F(x)= 1/(x+2)(x-5)
Answers
The graph of the rational equation is solved and f ( x ) = 1/ ( x + 2 ) ( x - 5 )
Given data ,
Let the function be represented as f ( x )
Now , the value of f ( x ) is
f ( x ) = 1/ ( x + 2 ) ( x - 5 )
The function will have increasingly large values as the denominator approaches zero. When x -2, the denominator is positive and the function tends to the upside. When x -2 x 5, the function is negative. When x 5, the function becomes positive once more.
Hence , the rational function is f ( x ) = 1/ ( x + 2 ) ( x - 5 )
To learn more about rational functions click :
https://brainly.com/question/26594994
#SPJ1
The complete question is attached below :
Which of the following rational functions is graphed below?
A. F(x) =(x-2)/(x+5)
B. F(x) =1/(x-2)(x + 5)
C. F(x) =1/(2x + 5)
D. F(x)= 1/(x+2)(x-5)

X to the third power equals 512
Answers
Answer:
8
Step-by-step explanation:
Rectangle STUV is shown on a coordinate plane.
Rectangle STUV with vertices S at negative 7 comma 6, T at negative 2 comma 6, U at negative 2 comma 1, and V at negative 7 comma 1.
If rectangle STUV is translated using the rule (x, y) → (x − 2, y − 4) and then rotated 90° counterclockwise, what is the location of T″?
Answers
To find the location of T″ after translating and rotating the rectangle, let's follow the given steps:
1. Translation: The translation rule (x, y) → (x − 2, y − 4) moves each point of the rectangle 2 units to the left and 4 units downwards.
After translation:
S' (-7 - 2, 6 - 4) = (-9, 2)
T' (-2 - 2, 6 - 4) = (-4, 2)
U' (-2 - 2, 1 - 4) = (-4, -3)
V' (-7 - 2, 1 - 4) = (-9, -3)
2. Rotation: The rotation of 90° counterclockwise swaps the x and y coordinates while changing the sign of the new x-coordinate.
After rotation:
S" (2, -9)
T" (2, -4)
U" (-3, -4)
V" (-3, -9)
Therefore, the location of T″ after the translation and rotation is at coordinates (2, -4).
To find the location of T″, we need to apply the given translation and rotation transformations to the original rectangle STUV.
Explanation:To find the location of T′′, we need to follow the given transformations.
Translate the rectangle using the rule (x, y) → (x - 2, y - 4). This means that we subtract 2 from the x-coordinate and 4 from the y-coordinate of each vertex.After translating, we rotate the rectangle 90° counterclockwise. This means that we swap the x and y coordinates of each vertex and negate the new x-coordinate.Let's apply these transformations step by step:
Translation:
S (-7, 6) → (-7 - 2, 6 - 4) = (-9, 2)
T (-2, 6) → (-2 - 2, 6 - 4) = (-4, 2)
U (-2, 1) → (-2 - 2, 1 - 4) = (-4, -3)
V (-7, 1) → (-7 - 2, 1 - 4) = (-9, -3)
Rotation:
S′ (-9, 2) → (2, -9)
T′′ (-4, 2) → (-2, -4)
U′ (-4, -3) → (3, -4)
V′ (-9, -3) → (-3, -9)
Therefore, the location of T′′ is (-2, -4).
Learn more about Location of T″ here:https://brainly.com/question/14134437
#SPJ11
PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP PLEASE HELP


Answers
Answer: A,B,E,F
Step-by-step explanation:
Answer:
The answer is A, B, E, F
Step-by-step explanation:
Find the product write the product in simplest form 1 1/7 x 1 3/4
Answers
2 25/28
1 1/7 x 1 3/4
7+1=8 4+3=7
8/7 + 7/4
x4 x7
32/28 + 49/28= 81/28
28 x 2 = 56
81-56=25
2 25/28
So, the answer is 56/28
16x^2-1=0
help algebra 2
Answers
Answer:
16x²=1
x²=1/16
x=√(1/16)
x=+- (1/4)
Solve the inequality - 6 x > 42
what happens to the inequality sign when you divide by a negative number
Answers
Answer:
the inequality sign changes when dividing by a negative number

Answer:
x < -7
Step-by-step explanation:
-6x > 42
First you want to divide off -6 to isolate x
\(\frac{-6x}{-6}\) = \(\frac{42}{-6}\)
keeping in mind what you do to one side of the equation you have to do to the other side.
Whenever you divide with a negative number the inequality sign flips from < to > and vice versa.
after you divide off the -6 your left with x < \(\frac{42}{-6}\) which equals -7.
Hope this helps.
8+2x-4=6+2(x+1) please help
Answers
Answer:
Step-by-step explanation:
Which expression is a way to represent the ratio of g to h? A:hg B:h:g C;gh D;h × g
Answers
Answer:
B
Step-by-step explanation:
traditional notation states h:g
which is h/g
In the number 725.78, how does the value of the 7 in the tenths place compare to the value of the 7 in the hundreds place?
Answers
Answer:
C. 1/1,000
Step-by-step explanation:
yes or no ?
Michelle bought 30 marbles at the flea market. She wants to put them into little bags with 6 marbles in each bag. How many bags will she need?
Answers
Find the coordinates that will make this equation true? PLEASE HELP!!!

Answers
Answer:
2.4 makes it true!
I love you
yea yea yea yea yea
Step-by-step explanation:
turning point of y=(x+3)(x-7)
Answers
Explanation:
Let's find the roots aka x intercepts.
Plug in y = 0 and solve for x.
y=(x+3)(x-7)
(x+3)(x-7) = 0
x+3 = 0 or x-7 = 0
x = -3 or x = 7 are the two roots.
Now find the midpoint of those roots.
Add them up and divide in half.
(-3+7)/2 = 4/2 = 2
The midpoint happens at x = 2, which is the x coordinate of the vertex. This is the axis of symmetry where the vertex is located.
The vertex in this case is the lowest point on the parabola. It's the turning point where it goes from decreasing to increasing.
Plug x = 2 back into the original equation to find its paired y value.
y=(x+3)(x-7)
y=(2+3)(2-7)
y=(5)(-5)
y=-25
Therefore, the vertex is located at (2, -25) as indicated in the graph below. I used GeoGebra to make the graph. Desmos is another good choice.

F(x)=-3(x-1) find f(0)
Answers
Answer: 3 (x-1)
______
x
Step-by-step explanation:
so thats 3(x-1) over x
have a good day! :)
plz give me brainliest
Answer:
3
Step-by-step explanation:
F(x)=-3(x-1) find f(0)
F(0) = -3(0-1)
F(0) = -3(-1)
F(0)= 3
someone pls help me for brainleist

Answers
Answer:
x = 72°
Step-by-step explanation:
The angle is a right angle meaning it is equal to 90°. You can tell it is a right angle because of the small square in the corner of the angle.
Because both angles are equal to 90° you can simply do the equation \(90-18=x\)
which leaves you with the answer x = 72
90-18 =72
Remember that a square angle measures 90°..then sybstract what you know
Please help asap see the picture down below and answer

Answers
Parts of similar triangles
Find x

Answers
The value of x in the triangle is 16.
Triangle – what is it?The trigon, a 3-sided polygon, is sometimes (though not often) referred to as a triangle. There are three sides and three angles in every triangle, some of which may be the same.
Due to the similarity between the triangles ABC and ADE, we may establish the following ratio:
BC/DE = AB/AD
Inputting the values provided yields:
8/x = 12/24
When the right-hand side of the equation is simplified, we obtain:
12/24 = 1/2
Adding this value to the proportion results in:
8/x = 1/2
If we cross-multiply, we obtain:
2*8 = x
The left side of the equation can be simplified to: 16 = x.
To know more about triangle visit:-
https://brainly.com/question/2773823
#SPJ1
The diameter of a proton is about 1.9 cross times 10 to the power of short dash 15 end exponent meters. A hydrogen atom has an overall length of 100,000 times (or 1 cross times 10 to the power of 5 times) the diameter of a proton.
What is the length of the hydrogen atom, in meters, if it were written in scientific notation?
A. 1.9 x 10 (15 exponent)
B. 1.9 x 10 (-15 exponent)
C. 1.9 x 10 (-8 exponent)
D. 1.9 x 10 (-12 exponent)
Answers
Using scientific notation, the measure is given as follows:
\(1.9 \times 10^{-10}\)
What is scientific notation?A number in scientific notation is given by:
\(a \times 10^b\)
With the base being \(a \in [1, 10)\).
The diameter of a proton, in scientific notation, is given by:
\(1.9 \times 10^{-15}\).
The hydrogen atom has an overall length of 100,000 = 10^5 times the diameter of the proton, hence the length is given by:
\(L = 100000 \times 1.9 \times 10^{-15} = 10^5 \times 1.9 \times 10^{-15} = 1.9 \times 10^{5 - 15} = 1.9 \times 10^{-10}\)
For the above length, I applied the multiplication of factors with the same base and different exponents, where we keep the base and add the exponents.
More can be learned about scientific notation at https://brainly.com/question/16394306
#SPJ1
f
3
+ 22 = 17
- 22 - 22 +
43
f = -5
3
= 3(-5)
f =
Subtract 22 on both sides.
Multiply by 3 on both sides.
Answers
On solving the provided question, by the help of BODMAS we can say that - Subtract 22 from both sides is the answer to the given question.
What is BODMAS?
BODMAS and PEDMAS are both names for it in various places. This stands for exponents, parenthesis, division, multiplication, addition, and subtraction. The BODMAS rule states that parentheses must be answered before powers or roots (that is, of), divisions, multiplications, additions, and lastly subtractions. The BODMAS rule states that the degree (52 = 25), parenthesis (2 + 4 = 6), any division or multiplication (3 x 6 (bracket response) = 18), and any addition or subtraction (18 + 25 = 43) come before any other operations.
\(f/3 +22 = 17\)
\(f/3 +22 -22 = 17 -22\) Subtracting the same value from both sides keeps the equation equal.
Then simplify. The \(+22 and -22= 0\) They "cancel" \(17-22 = -5\)
\(f/3 = -17 f/3\) is now isolated-- by itself-- in the equation.
If we have to solve f, the next step we to take is to multiply on the both sides by 3.
To know more about BODMAS visit:
https://brainly.com/question/29795897
#SPJ1
The one-to-one functions g and h are defined as follows.g(x) = -2x-13h=(-7 -2) (8)12I
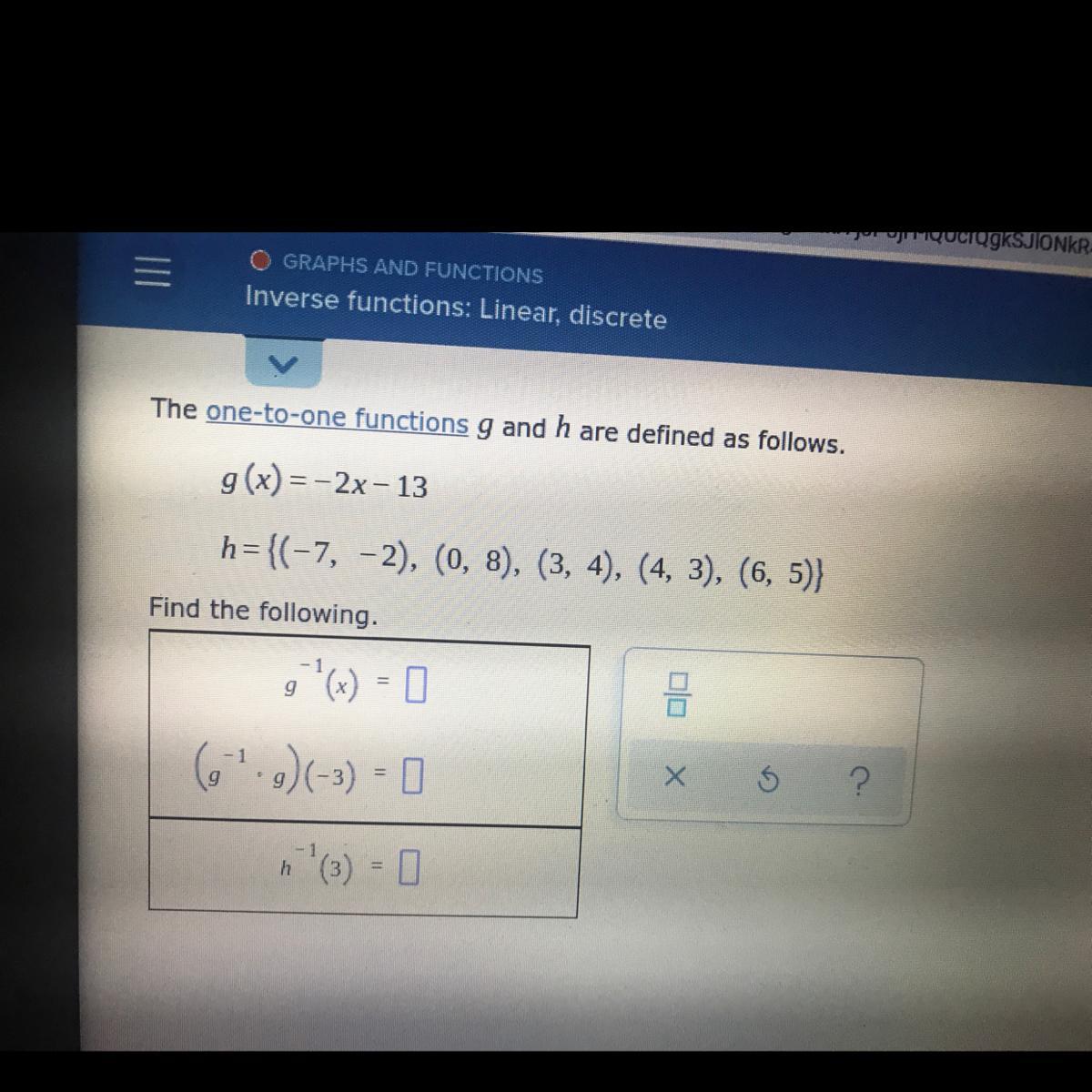
Answers
We have to remember that in one-to-one functions each element of the domain maps to a different element in the range.
When we have a bijection we have that each element in the set A, for example, corresponds to exactly one element of B, and vice versa.
When we have a bijection, we also have an inverse function.
Then, we have that:
\(g(x)=-2x-13\)To find the inverse, we have to interchange the variables:
\(y=-2x-13\)Now, we have:
\(x=-2y-13\)And we need to solve for y:
1. Add 13 to both sides of the equation:
\(x+13=-2y-13+13\Rightarrow x+13=-2y\)2. Divide both sides by -2:
\(\frac{(x+13)}{-2}=\frac{-2y}{-2}\Rightarrow-\frac{(x+13)}{2}=y\)Then, we have that:
\(g^{-1}(x)=-\frac{(x+13)}{2}\)We can check this if we make a composition between the two functions (then we will get x as a result).
\((g^{-1}\circ g)=g^{-1}(g(x))=-\frac{((-2x-13)+13)_{}}{2}=-\frac{(-2x)}{2}=\frac{2x}{2}=x\)Then, we have that the result for this composition is equal to x. Thus:
\((g^{-1}\circ g)(-3)=-3^{}\)We also have that:
We have that h(4) = 3, then h^(-1)(3) = 4 or
\(h(4)=3\Rightarrow h^{-1}(3)=4\)In summary, we have:
\(g^{-1}(x)=-\frac{(x+13)}{2}\)\((g^{-1}\circ g)(-3)=-3\)\(h^{-1}(3)=4\)

Jenna parks her car at a parking lot for a flat fee of $5.00 plus $0.75 per hour that her car is parked.
(a) Write an equation to represent Elaine's total parking cost, C, in dollars, for t hours.
(b) How much will it cost Elaine to park her car for a full 24 h?
PLEASE HELP!!!
Answers
a. C = 5.00 + 0.75t
b. It will cost Elaine $23.00 to park her car for a full 24 hours at the parking lot.
(a) To represent Elaine's total parking cost, C, in dollars for t hours, we can use the following equation:
C = 5.00 + 0.75t
In this equation, the constant term 5.00 represents the flat fee for parking, and the term 0.75t represents the additional cost per hour based on the number of hours (t) the car is parked. By adding the flat fee to the hourly cost, we get the total parking cost for t hours.
(b) To find out how much it will cost Elaine to park her car for a full 24 hours, we can substitute t = 24 into the equation:
C = 5.00 + 0.75 * 24
Calculating this expression, we get:
C = 5.00 + 18.00
C = 23.00
Therefore, it will cost Elaine $23.00 to park her car for a full 24 hours at the parking lot.
for such more question on cost
https://brainly.com/question/25109150
#SPJ8
78is 75% of what number?

Answers
Answer: the third one and the actual answer is 104
Step-by-step explanation:
Solve for the variable: 3(x+2) - 9 = 15 - 4(5x - 2)
Make sure you round you answer to the nearest whole number
Answers
Answer:
x=1.13
Step-by-step explanation:
isolate the variable and the numbers and solve.
explain the types of frequency distribution in statistics
Answers
The two types of frequency distributions are Discrete Frequency Distribution and Grouped Frequency Distribution
What are the types of distribution?The two types of frequency distributions are;
Discrete Frequency Distribution:Grouped Frequency DistributionWhen the data consists of discrete, separate values, this sort of distribution is used. It displays the frequency or number of occurrences of each value.
The data is often expressed in a table with two columns: one for distinct values and another for the frequencies of those values.
This distribution is utilized when the data is continuous and has a wide range of values. It entails categorizing the data into intervals or classes and then calculating the frequency of values that fall within each interval.
Learn more about frequency distribution at: https://brainly.com/question/27820465
#SPJ1
PLEASE HELPPP!!!!SOMEONEEEE

Answers
Answer:
(i) x ≤ 1
(ii) ℝ except 0, -1
(iii) x > -1
(iv) ℝ except π/2 + nπ, n ∈ ℤ
Step-by-step explanation:
(i) The number inside a square root must be positive or zero to give the expression a real value. Therefore, to solve for the domain of the function, we can set the value inside the square root greater or equal to 0, then solve for x:
\(1-x \ge 0\)
\(1 \ge x\)
\(\boxed{x \le 1}\)
(ii) The denominator of a fraction cannot be zero, or else the fraction is undefined. Therefore, we can solve for the values of x that are NOT in the domain of the function by setting the expression in the denominator to 0, then solving for x.
\(0 = x^2+x\)
\(0 = x(x + 1)\)
\(x = 0\) OR \(x = -1\)
So, the domain of the function is:
\(R \text{ except } 0, -1\)
(ℝ stands for "all real numbers")
(iii) We know that the value inside a logarithmic function must be positive, or else the expression is undefined. So, we can set the value inside the log greater than 0 and solve for x:
\(x+ 1 > 0\)
\(\boxed{x > -1}\)
(iv) The domain of the trigonometric function tangent is all real numbers, except multiples of π/2, when the denominator of the value it outputs is zero.
\(\boxed{R \text{ except } \frac{\pi}2 + n\pi} \ \text{where} \ \text{n} \in Z\)
(ℤ stands for "all integers")
Answer:
(i) x ≤ 1
(ii) All real numbers except x = 0 and x = -1.
(iii) x > -1
(iv) All real numbers except x = π/2 + πn, where n is an integer.
Step-by-step explanation:
What is the domain?The domain of a function is the set of all possible input values (x-values).
\(\hrulefill\)
\(\textsf{(i)} \quad f(x)=\sqrt{1-x}\)
For a square root function, the expression inside the square root must be non-negative. Therefore, for function f(x), 1 - x ≥ 0.
Solve the inequality:
\(\begin{aligned}1 - x &\geq 0\\\\1 - x -1 &\geq 0-1\\\\-x &\geq -1\\\\\dfrac{-x}{-1} &\geq \dfrac{-1}{-1}\\\\x &\leq 1\end{aligned}\)
(Note that when we divide or multiply both sides of an inequality by a negative number, we must reverse the inequality sign).
Hence, the domain of f(x) is all real numbers less than or equal to -1.
\(\boxed{\begin{aligned} \textsf{Inequality notation:} \quad &x \leq 1\\\textsf{Interval notation:} \quad &(-\infty, 1]\\\textsf{Set-builder notation:} \quad &\left\{x \in \mathbb{R}\left|\: x \leq 1 \right\} \end{aligned}}\)
\(\hrulefill\)
\(\textsf{(ii)} \quad g(x) = \dfrac{1}{x^2 + x}\)
To find the domain of g(x), we need to identify any values of x that would make the denominator equal to zero, since division by zero is undefined.
Set the denominator to zero and solve for x:
\(\begin{aligned}x^2 + x &= 0\\x(x + 1) &= 0\\\\\implies x &= 0\\\implies x &= -1\end{aligned}\)
Therefore, the domain of g(x) is all real numbers except x = 0 and x = -1.
\(\boxed{\begin{aligned} \textsf{Inequality notation:} \quad &x < -1 \;\;\textsf{or}\;\; -1 < x < 0 \;\;\textsf{or}\;\; x > 0\\\textsf{Interval notation:} \quad &(-\infty, -1) \cup (-1, 0) \cup (0, \infty)\\\textsf{Set-builder notation:} \quad &\left\{x \in \mathbb{R}\left|\: x \neq 0,x \neq -1 \right\} \end{aligned}}\)
\(\hrulefill\)
\(\textsf{(iii)}\quad h(x) = \log_7(x + 1)\)
For a logarithmic function, the argument (the expression inside the logarithm), must be greater than zero.
Therefore, for function h(x), x + 1 > 0.
Solve the inequality:
\(\begin{aligned}x + 1 & > 0\\x+1-1& > 0-1\\x & > -1\end{aligned}\)
Therefore, the domain of h(x) is all real numbers greater than -1.
\(\boxed{\begin{aligned} \textsf{Inequality notation:} \quad &x > -1\\\textsf{Interval notation:} \quad &(-1, \infty)\\\textsf{Set-builder notation:} \quad &\left\{x \in \mathbb{R}\left|\: x > -1\right\} \end{aligned}}\)
\(\hrulefill\)
\(\textsf{(iv)} \quad k(x) = \tan x\)
The tangent function can also be expressed as the ratio of the sine and cosine functions:
\(\tan x = \dfrac{\sin x}{\cos x}\)
Therefore, the tangent function is defined for all real numbers except the values where the cosine of the function is zero, since division by zero is undefined.
From inspection of the unit circle, cos(x) = 0 when x = π/2 and x = 3π/2.
The tangent function is periodic with a period of π. This means that the graph of the tangent function repeats itself at intervals of π units along the x-axis.
Therefore, if we combine the period and the undefined points, the domain of k(x) is all real numbers except x = π/2 + πn, where n is an integer.
\(\boxed{\begin{aligned} \textsf{Inequality notation:} \quad &\pi n\le \:x < \dfrac{\pi }{2}+\pi n\quad \textsf{or}\quad \dfrac{\pi }{2}+\pi n < x < \pi +\pi n\\\textsf{Interval notation:} \quad &\left[\pi n ,\dfrac{\pi }{2}+\pi n\right) \cup \left(\dfrac{\pi }{2}+\pi n,\pi +\pi n\right)\\\textsf{Set-builder notation:} \quad &\left\{x \in \mathbb{R}\left|\: x \neq \dfrac{\pi}{2}+\pi n\;\; (n \in\mathbb{Z}) \right\}\\\textsf{(where $n$ is an integer)}\end{aligned}}\)




what should be added to -13/25+21/5+-21/18 to get 5?
Answers
ATQ,
= \( \dfrac{ - 13}{25} + \dfrac{21}{5} + \frac{ - 21}{18} + x = 5\)
Take the lcm of 25,5,18 and then manipulate it accordingly.= \( \dfrac{ 377}{150} + x = 5\)
= \( x = 5 - \dfrac{ 377}{150}\)
= \( x = \dfrac{ 373}{150}\)
Answer
=727/150
Step-by-step explanation:
-13/25 + 21/18 + 21/18
= -13 + 105/25 + 21/18
= 92/25 + 21/18
= 1656 + 525/450
= 2181/450 = 727/150
Have nice day
can't rely see it lol

Answers
Answer:
x = 60
Step-by-step explanation:
Answer:
x = 60°
Step-by-step explanation:
we know that triangles have 180 degrees so we can set up an equation:
86 + 34 + x = 180
now we subtract the sum of 86 and 34 from both sides to get a final answer:
x = 60
so lets plug our x value into the previous equation to check our answer:
86 + 34 + 60 = 180
when we add these numbers together, the equation checks out so we know our answer is correct.
hope this helps!
heres a list of numbers 3 6 9 7 4 6 7 0 7 Find median,mean,range and mode
Answers
median=order them and find the middle=6
mean=add them all up and divide by the amount of numbers=(3+6+9+7+4+6+7+0 +7)/9=5.4
range= the difference between the smallest and largest number=9-3=6
mode= the one that appears the most= 7
The median, mean, range and mode will be 6, 5.4, 9 and 7.
The median is the number in the middle when arranged in an ascending order. The numbers will be:
0, 3, 4, 6, 6, 7, 7, 7, 9.
The median is 6.
The range is the difference between the highest and lowest number which is: = 9 - 0 = 9
The mode is the number that appears most which is 7.
The mean will be the average which will be:
= (0 + 3 + 4 + 6 + 6 + 7 + 7 + 7 + 9) / 9.
= 49/9
= 5.4
Read related link on:
https://brainly.com/question/9426296

