PLEASE HELP
What is the domain of a quadratic functions that opens up or down?
Answers
Related Questions
2 1/12 divided 2 5/8 fractions
Answers
Answer: 50/63 or 0.793650
Step-by-step explanation:
arun is older than suav. their ages are consecutive integers. find arun's age if the sum of the square of arun's age and 4 times suav's age is 92.
Answers
If the ages of Arun and Suav are consecutive integers than the Arun's age is 8 years .
In the question ,
it is given that ,
Arun is older than Suav ,
and their ages are consecutive integers ,
Let the Suav's age be = "x"
So , the Arun's age be = "x+1" .
it is given that , the sum of the square of Arun's age and 4 times Suav's age is 92.
that means ;
(x+1)² +4x = 92
x² +6x + 1 = 92
x² + 6x - 91 = 0
Solving the quadratic equations ,
we get ,
x = 7 and x = -13 .
age cannot be negative , So ,
x = 7 ,
thus, the Arun's age will be = 7 + 1 = 8 years.
Therefore , the age of Arun is 8 years .
Learn more about Age here
https://brainly.com/question/17082588
#SPJ4
Renata is purchasing a condominium for $125,000. She wants to put down a down payment of 20%. Select all the true statements. The proportion that represents the down payment is 20100=125,000 20 100 = 125 , 000 x . The down payment is $25,000. The proportion that represents the down payment is 20100=125,000 20 100 = x 125 , 000 . The down payment is $50,000. The down payment is 15 1 5 of the cost of the house.
Answers
The correct options are -
The proportion that represents the down payment is : 20/100 x 125000.The down payment is $25,000What is down payment?When something is bought on credit, an initial payment is made in the form of a down payment.
Given is that Renata is purchasing a condominium for $125,000. She wants to put down a down payment of 20%.
We can calculate the amount she is putting in down payment as -
{x} = 20% of 125000
{x} = 20/100 x 125000
{x} = 20 x 1250
{x} = 25000
Therefore, the correct options are -
The proportion that represents the down payment is : 20/100 x 125000.The down payment is $25,000To solve more questions on functions & equations, visit the link-
https://brainly.com/question/29014197
#SPJ9
The Venn diagram below shows the events A and B, and the probabilities p, q and r.
It is known that P(A)=0.43 , P(B)=0.62 and P(A∩B)=0.27 .
Calculate the value of p
Calculate the value of q
Calculate the value of r
Find the value of P (A given NOT B)
Answers
The value of q is 0.35.
The value of p is 0.16.
The value of r is 0.27.
The value of P(A given NOT B) is approximately 0.4211.
To calculate the values of p, q, and r, we can use the information provided in the Venn diagram and the probabilities of events A and B.
Given:
P(A) = 0.43
P(B) = 0.62
P(A∩B) = 0.27
Calculating the value of p:
The value of p represents the probability of event A occurring without event B. In the Venn diagram, p corresponds to the region inside A but outside B.
We can calculate p by subtracting the probability of the intersection of A and B from the probability of A:
p = P(A) - P(A∩B)
= 0.43 - 0.27
= 0.16
Therefore, the value of p is 0.16.
Calculating the value of q:
The value of q represents the probability of event B occurring without event A. In the Venn diagram, q corresponds to the region inside B but outside A.
We can calculate q by subtracting the probability of the intersection of A and B from the probability of B:
q = P(B) - P(A∩B)
= 0.62 - 0.27
= 0.35
Therefore, the value of q is 0.35.
Calculating the value of r:
The value of r represents the probability of both event A and event B occurring. In the Venn diagram, r corresponds to the intersection of A and B.
We are given that P(A∩B) = 0.27, so the value of r is 0.27.
Therefore, the value of r is 0.27.
Finding the value of P(A given NOT B):
P(A given NOT B) represents the probability of event A occurring given that event B does not occur. In other words, it represents the probability of A happening when B is not happening.
To calculate this, we need to find the probability of A without B and divide it by the probability of NOT B.
P(A given NOT B) = P(A∩(NOT B)) / P(NOT B)
We can calculate the value of P(A given NOT B) using the provided probabilities:
P(A given NOT B) = P(A) - P(A∩B) / (1 - P(B))
= 0.43 - 0.27 / (1 - 0.62)
= 0.16 / 0.38
≈ 0.4211
Therefore, the value of P(A given NOT B) is approximately 0.4211.
for such more question on value
https://brainly.com/question/27746495
#SPJ8
Need help quick please

Answers
Answer:-1/6
Step-by-step explanation:
Draw a line out in the 2nd quadrant.
Your y=\(\sqrt{35}\) hypotenuse=6 use pythagorean theorem to solve for x
6² = 35 + x²
x=1
so
cosΘ = -1/6
Which value is not valid for a probability?
3/7
7/3
0.333
80%
Answers
Answer: 0.333
you cant make that a whole percent and it's not a fraction.
Solve (x+1)2 =13/4 using the square root property
Answers
Answer:
Starting with the equation:
(x + 1)^2 = 13/4
We can use the square root property, which states that if a^2 = b, then a is equal to the positive or negative square root of b.
Taking the square root of both sides, we get:
x + 1 = ±√(13/4)
Simplifying under the radical:
x + 1 = ±(√13)/2
Now we can solve for x by subtracting 1 from both sides:
x = -1 ± (√13)/2
Therefore, the solutions to the equation are:
x = -1 + (√13)/2 or x = -1 - (√13)/2
Step-by-step explanation:
3 6 9 12 15 18 21 24 27 30 is odd or even numbers?
Answers
Answer: Half of them are even and half of them are odd.
Step-by-step explanation:
The even numbers are 6, 12, 18, 24, and 30. An even number is defined as a number that is divisible by 2, meaning it has no remainder when divided by 2. For example, 6 divided by 2 equals 3 with no remainder, so 6 is even.
The odd numbers are 3, 9, 15, 21, and 27. An odd number is defined as a number that is not divisible by 2, meaning it has a remainder of 1 when divided by 2. For example, 9 divided by 2 equals 4 with a remainder of 1, so 9 is odd.
Therefore, out of the given numbers, half of them are even and half of them are odd.
________________________________________________________
A circle with center O(4,2) contains the point A(1,6),
MIM
0(44)
Write a subtraction expression for each length OB and AB:
OBX-2 AB-y+h
Answers
A subtraction expression for each length OB and AB is \(OBX = \sqrt (x - 4)^2 + (y - 2)^2] + 2 \sqrt (1 - x)^2 + 16] - y.\)
What is the property of circle?Let r be the radius of the circle. Then we have:
r = distance(O, B)
We can use the distance formula to find the distance between two points:
distance(P, Q) = √[(x2 - x1)² + (y2 - y1)²]
where P = (x1, y1) and Q = (x2, y2)
Substituting O = (4, 2) and B = (x, y), we get:
r = distance(O, B) = √[(x - 4)² + (y - 2)²]
Now, let's consider the subtraction expression:
OBX-2 AB-y+h
We can simplify this expression as follows:
\(OBX = r + 2 AB = \sqrt{[(x - 4)^2 + (y - 2)^2] } + \sqrt[2]{[(1 - x)^2 + (6 - y)^2]}\)
We don't need to include the variables y and h in the expression since they were not defined in the problem. So the final subtraction expression for OBX is:
\(OBX = \sqrt{ [(x - 4)^2 + (y - 2)^2]} + \sqrt[2]{[(1 - x)^2 + 6]-y} .\)
Therefore, the expression is OBX \(= \sqrt(x - 4)^2 + (y - 2)^2] + 2 \sqrt(1 - x)^2 + 16] - y.\)
Learn more about circle here:
https://brainly.com/question/11833983
#SPJ1
4.0 = (0.40+ x)²/(0.15 - x)^2
solve for x
Answers
Answer:
-0.03334
Step-by-step explanation:
i just graphed it and looked at were y=4 and gave you the x value
:)
Answer:
x1 = -0.0333333, x2=0.7





An opinion poll reported that 36% believe a certain governor broke campaign financing laws in his election campaign. How many people would you have to survey to be 99% confident that you can estimate to within 1% the fraction of people who believe the governor broke campaign financing laws? Round your answer to whole number.
Answers
Answer:
The number of people would have participate in opinion poll
n = 15,267
Step-by-step explanation:
Step(i):-
Given data an opinion poll reported that 36% believe a certain governor broke campaign financing laws in his election campaign.
Given proportion = 36% =0.36
Given the margin of error = 1% =0.01
Level of significance = 99% 0 r 0.01
Z₀.₀₁ = 2.576
step(ii):-
The margin of error of Population proportion is determined by
\(M.E = \frac{Z_{0.01} \sqrt{p(1-p)} }{\sqrt{n} }\)
\(0.01 = \frac{2.576 \sqrt{0.36(1-0.36)} }{\sqrt{n} }\)
\(\sqrt{n} = \frac{2.576 \sqrt{0.36(1-0.36)} }{0.01 }\)
√n = 123.648
Squaring on both sides , we get
n = 15,267
final answer:-
The number of people would have participate in opinion poll
n = 15,267
Find all possible values of x.
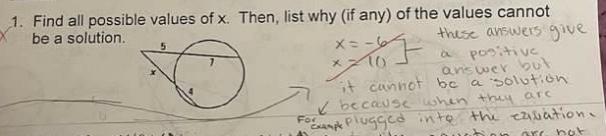
Answers
The possible values of x in the circle using the theorem of intersecting secants are x = 7.38 and x = -11.38
Finding all possible values of x.From the question, we have the following parameters that can be used in our computation:
The intersecting secants
Using the theorem of intersecting secants, we have the following equation
(5 + 7) * 7 = (x + 4) * x
When the sum is evaluated, we have
12 * 7 = (x + 4) * x
When the product is evaluated, we have
84 = x² + 4x
So, we have
x² + 4x - 84 = 0
When solved for x, we get
x = 7.38 and x = -11.38
The value of x = -11.38 cannot be used
This is because x cannot be negative
Read more about intersecting secants at
https://brainly.com/question/26340897
#SPJ1
3. Square SQRE has coordinates S(2, 2) Q (5,2)R (5. – 1). Find the coordinates of E. I gotta turn it in tomorrow
Answers
Given:
Square SQRE has coordinates S(2, 2) Q (5,2), and R (5. – 1).
To find:
The coordinates of E.
Explanation:
Let (x, y) be the coordinates of E.
Using the midpoint formula,
\(p=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)As we know,
The diagonals of the square are intersected by its midpoint.
So, the Midpoint of SR and QE is the same in a given square SQRE.
\(\begin{gathered} Midpoint\text{ of SR = Midpoint of QE} \\ (\frac{2+5}{2},\frac{2-1}{2})=(\frac{5+x}{2},\frac{2+y}{2}) \\ (\frac{7}{2},\frac{1}{2})=(\frac{5+x}{2},\frac{2+y}{2}) \end{gathered}\)Equating the coordinates we get,
\(\begin{gathered} \frac{7}{2}=\frac{5+x}{2} \\ 7=5+x \\ x=2 \\ \frac{1}{2}=\frac{2+y}{2} \\ 1=2+y \\ y=-1 \end{gathered}\)Therefore, the coordinate of E is (2, -1).
Final answer:
The coordinate of E is (2, -1).
In the figure below, mWXZ = 95°, and m2 is four times mZ1. Find m2 1.
W
2
m21-0°
X
M<1

Answers
m2 be 4x
4x+x=95
5x=95
x=95/5
x=19
m1 is 19
Complete each equation so that it has infinitely many solution
(Dont mind the exercise underneath)
(Brainliest to correct answer)

Answers
The equation with an infinite number of solutions is 12x-x+8+3x=14x+8.
What is equation?An equation is a formula in mathematics that expresses the equality of two expressions by connecting them with the equals sign =. In its most basic form, an equation is a mathematical statement that shows that two mathematical expressions are equal. 3x + 5 = 14, for example, is an equation in which 3x + 5 and 14 are two expressions separated by a 'equal' sign. A mathematical equation that depicts the relationship between two expressions on opposite sides of the sign. It mostly consists of one variable and one equal to symbol. 2x - 4 = 2 is an example.
Here,
12x-x+8+3x=14x+8
The equation so that it has infinitely many solution is 12x-x+8+3x=14x+8.
To know more about equation,
https://brainly.com/question/2228446
#SPJ1
Enter the digit that can replace (blank box) 526 < 5 _ 5 < 541 The digit that fits in the gray box is ?
Answers
3
1) The number to be found, is a multiple of 5 and also greater than 526 but also lesser than 541.
2) So we have, the next number whose last digit is 5 immediately greater than 526 and lesser than 541 is 535
3) So 3 is the missing digit
1 point A ship's sonar finds that the angle of depression to a wreck on the bottom of the ocean is 13.2°. If a point on the ocean floor is 75 meters directly below the ship, how many meters is it from that point on the ocean floor to the wreck? Round to the nearest tenth.
Answers
Check the picture below.
Make sure your calculator is in Degree mode.

The number of meters from that point on the ocean floor to the wreck is 319.83 meters.
What are trigonometric identities?There are three commonly used trigonometric identities.
Sin x = 1/ cosec x
Cos x = 1/ sec x
Tan x = 1/ cot x or sin x / cos x
Cot x = cos x / sin x
We have,
From the figure,
Tan 13.2° = 75 / x
x = 75/tan 13.2°
x = 75/0.2345
x = 319.829 meters
x = 319.83 meters
Thus,
The distance from the point to the wreck is 319.83 meters.
Learn more about trigonometric identities here:
https://brainly.com/question/14746686
#SPJ2

I need 23 questions answered

Answers
The surface area of a rectangular prism is 48 5/6 mi².
How to calculate the surface area of a rectangular prism?In Mathematics and Geometry, the surface area of a rectangular prism can be calculated and determined by using this mathematical equation or formula:
Surface area of a rectangular prism = 2(LH + LW + WH)
Where:
L represents the length of a rectangular prism.W represents the width of a rectangular prism.H represents the height of a rectangular prism.By substituting the given side lengths into the formula for the surface area of a rectangular prism, we have the following;
Surface area of rectangular prism = 2[6 × 2 1/3 + (1 1/4 × 6) + (1 1/4 × 2 1 /3)]
Surface area of rectangular prism = 2[14 + 15/2 + 35/12]
Surface area of rectangular prism = 48 5/6 mi².
Read more on surface area of a rectangular prism here: brainly.com/question/28185251
#SPJ1
I need help with this

Answers
Answer:
90 degrees
Step-by-step explanation:
Hope thishelps. :) :D
Power Function:
Exercise: Recognize and analyze the graph of the power function as the exponent "n" and the coefficient "a" vary
1. Consider a positive exponent power function
A) Describe the graph of the function when n is even, for this you must attach an image of the graph of the function that meets these conditions.
B) Describe the graph of the function when n is odd, for this you must attach an image of the graph of the function that meets these conditions.
C) Describe what happened when the coefficient a is positive and also when it is negative. Is there any change in the graph?
D) Describe what happened when the coefficient a increases or decreases. What happens to the graph of the function?
2. Consider a negative exponent power function
A) Describe the graph of the function when n is even, for this you must attach an image of the graph of the function that meets these conditions.
B) Describe the graph of the function when n is odd, for this you must attach an image of the graph of the function that meets these conditions.
C) Describe what happened when the coefficient a is positive and also when it is negative. Is there any change in the graph?
D) Describe what happened when the coefficient a increases or decreases. What happens to the graph of the function?
Answers
Problem 1
Part A
If n is even, then we have a "parabolic" shape going on. I put that in quotes because if n = 2, then we have a true parabola; however, if n is even and larger than 2, then we have a curve that looks like a parabola, but it's not exactly a perfect parabola. All of these curves have in common that the end behavior is the same for the left and right sides.
Consider the example where a = 1 and n = 2. This means
y = a*x^n
turns into
y = 1*x^2
which is the same as
y = x^2
This produces the parent parabola curve. This curve opens upward.
I recommend using Desmos to graph y = a*x^n, where the 'a' and n are parameters set up. Check out the screenshot below.
---------------------
Part B
If n is odd, then we'll get something that looks like a cubic curve. If n = 3, then we get a cubic curve. If n is odd and n > 3, then we get something that looks like a cubic curve, but it's not exactly this perfect cubic.
If we let a = 2 and n = 3, then y = a*x^n becomes y = 2x^3. The graph of which is below.
---------------------
Part C
If a > 0 then the curve is like the previous examples shown earlier.
If a < 0, then we will reflect those given earlier curves over the horizontal x axis. An example is shown below using y = -x^2. This time we have a = -1 and n = 2. In other words, I reflected the example in part A over the x axis.
---------------------
Part D
As 'a' increases, then the graph gets more narrow. It also gets vertically stretched. Consider the example of going from y = 1x^2 to y = 3x^2 as shown below.
As 'a' decreases, then the process is done in reverse: the curve gets more flatter and wider horizontally. We consider the curve to be vertically compressed or squished. So we'd go from y = 3x^2 to y = 1x^2 as an example.
============================================================
Problem 2
Part A
For all of problem 2, we'll only consider negative values of n. We want n to be even, so let's say n = -2. Furthermore, let's say a = 2.
This means y = ax^n becomes y = 2x^(-2) which is the same as y = 2/(x^2)
The curve we get is really two separate pieces. There's a gap or disconnect at x = 0 because of a division by zero error. One piece of the curve is always increasing, while the other piece is always decreasing.
---------------------
Part B
Since we want n to be odd and negative, let's say n = -1. We'll keep a = 2 the same as before.
That means y = ax^n becomes y = 2x^(-1) as shown in the diagram below. What we have is a hyperbola. This is a disconnected set of two curves that collectively entirely define this function in a visual sense. Note the gap when x = 0 due to the division by zero error.
Recall that y = 2x^(-1) is the same as y = 2/x
Again, I'm using Desmos to generate each of these graphs.
Similar to part A, the two pieces are disconnected. This curve is known as hyperbola. It's always increasing if a < 0, and it's always decreasing when a > 0.
---------------------
Part C
If 'a' is positive, then the graph of y = 2/(x^2) is entirely above the x axis (aka everything is positive). On the flip side, if 'a' is negative, then everything swaps to being negative. That will reflect the curve over the x axis to get what you see in the example below. We have a = -2 and n = 2.
---------------------
Part D
As 'a' increases, this means the graph spreads out. If 'a' decreases, then it gets more compressed.
An example is shown below going from y = 1/x to y = 3/x which shows expansion going on (reverse it to get a compression).
============================================================
Once again, the screenshots are shown below as examples.




How much would you have to deposit today to accumulate the SAME AMOUNT OF MONEY that $75 monthly payments at a rate of 3.5% compounding monthly for 10 years in an annuity would earn?

Answers
Answer:
7606.62
Step-by-step explanation:
Start by finding how much you will have through the annuity. The question isn't that clear, so i will just assume it's an annuity due.
\(p(\frac{(1+i)^n-1}{i})*(1+i)\\i=.035/12= .0029166667\\n=10*12=120\\p=75 (given)\\75\frac{(1+.0029166667)^{120}-1}{.0029166667}*(1+.0029166667)= 10788.814149\\\)
Now just equate this to a time 0 payment at the same rate
\(10788.814149=(1+.0029166667)^{120}*x\\x= 7606.6228603=7606.62\)
As a quick note, if you were supposed to assume that your annuity was an annuity immediate the answer would be 7584.50.
In a certain year, there were 88 female officials in Congress, which is comprised of the House of Representatives and the Senate. If there were 54 more female members of the House of Representatives than female senators, find the number of females in each house of Congress.
Answers
Answer:
71 in House of Representatives17 in SenateStep-by-step explanation:
Let h and s represent the numbers in the House and Senate, respectively. Then we have ...
h + s = 88
h - s = 54
Subtracting the second equation from the first gives ...
(h +s) -(h -s) = (88) -(54)
2s = 34 . . . . . simplify
s = 17 . . . . . . . divide by 2
h = 88 -17 = 71 . . . . find the other value using the sum equation
There were 71 females in the House of Representatives, and 17 females in the Senate.
Imagine the following scenario: A student is about to take the final exam and has completed all assignments except the final exam. Out of 100 possible Project Assignment points, they have received 61 points. Out of 100 possible Quiz points, they have received 54 points If the student wanted to receive an overall B grade in the class, what do they need to score on the final exam? Give your answer as a percentage rounded to the nearest for decimal place (no percentage sign necessary), e.g., if I calculated 99.68%. I would enter 99.7.
Project Assignments: 60%
quizzes: 10%
final exam:30%
Answers
Answer:
126.7 if B=80
93.3 if B=70
Step-by-step explanation:
Let F represent the student's score on the final exam, and let B represent the percentage required for a grade of B. Then we must have ...
0.60(61) +0.10(54) +0.30F = B
B = 0.30F +42
F = (B -42)/0.3
__
If a grade of B requires 80 points or more, then the required grade on the final is ...
F = (80 -42)/0.3 = 38/0.3 = 126 2/3
The student must get 126.7% on their final to achieve an overall average of 80.
__
If a grade of B requires 70 points or more, then the required grade on the final is ...
F = (70 -42)/0.3 = 28/0.3 = 93 1/3
The student must get 93.3% on their final to achieve an overall average of 70.
What is the value of -
3x + 2(y - 1)
when x = 4 and y = 3?
x + y²
Show your work.
Answers
Answer:
-8
Step-by-step explanation:
substitute
x=4
into -3x+2(y-1):
x=3
-3x4+2x(3-1)
-12+2x(3-1)
-12+2x2
-12+4
= -8
Answer:
first question ans is 16 and second is 13
Step-by-step explanation:
Given
x=4 and y=3
3x+2(y-1)
3×4+2(3-1)
3×4+2×2
12+4
16Ans
Second question is
x+y×y
4+3×3
4+9
13 Ans
The machinery in a cereal plant fills 350 g boxes of cereal. The specifications for the machinery permit for a certain amount of fill tolerance. It is found that the weights of filled cereal boxes are normally distributed with a mean of 350 g and a standard deviation of 4 g. What is the probability that a box of cereal is under filled by 5 g or more?
Answers
There is approximately an 89.44% probability that a box of cereal is underfilled by 5 g or more.
To find the probability that a box of cereal is underfilled by 5 g or more, we need to calculate the probability of obtaining a weight measurement below 345 g.
First, we can standardize the problem by using the z-score formula:
z = (x - μ) / σ
Where:
x = the weight value we want to find the probability for (345 g in this case)
μ = the mean weight (350 g)
σ = the standard deviation (4 g)
Substituting the values into the formula:
z = (345 - 350) / 4 = -1.25
Next, we can find the probability associated with this z-score using a standard normal distribution table or a statistical calculator.
The probability of obtaining a z-score less than -1.25 is approximately 0.1056.
However, we are interested in the probability of underfilling by 5 g or more, which means we need to find the complement of this probability.
The probability of underfilling by 5 g or more is 1 - 0.1056 = 0.8944, or approximately 89.44%.
Therefore, there is approximately an 89.44% probability that a box of cereal is underfilled by 5 g or more.
For more questions on probability
https://brainly.com/question/251701
#SPJ8
please help me with this question :)

Answers

Step-by-step explanation:
if you brought this in here correctly, oh, it is a real mystery !
common sense ! we need common sense !
what can I add to e.g. 15 to still keep the 15 ?
this works with any other number as well.
e.g. 1
I have 1.
how much can I add to 1 to still have 1 afterwards ?
1+? = 1
? = 0
right. there is no other solution, as there are also no miracles in math.
whatever is added, is then added. to remain unchanged we can only add 0.
so,
15 + something = 15 can only be true, if that something is 0.
something = |3x|
that means the absolute value of 3x, which will always be +3x even for negative x.
but it does not matter.
|3x| = 0 (has to be 0 to make the main statement true).
therefore, 3x = 0
therefore, x = 0.
so, they're is only one dot (a filled dot) at precisely 0 in the graph that makes this a true statement.
Verizon Wireless charges
$0.09 for every 5 text
messages sent. How much
is your bill if you send 75
texts?
Make this into a equation
Answers
Answer:
$1.35
Step-by-step explanation:
$0.09/5 = $0.018
75 x $0.018 = $1.35
can i be brainiest...
Select the two figures that are sThe tree in your friend's yard casts a shadow that is 27 feet long. Your friend is 5 feet tall and casts a shadow that is 4.5 feet long. What is the height of the tree?similar to the 5 by 10 figure that is shown.
Answers
Answer: 30 ft tall
Step-by-step explanation: X= the height of the tree in feet
27/x = 4.5/5
(4.5)(x) = (27)(5)
(4.5)(x) = 135
divide by 4.5 to isolate x
135/4.5 = 30
x = 30
the tree is 30 ft tall
Suppose A and B are two events. Write expressions involving unions, intersections, and complements that describe the following
a) Both events occur
b) At least one event occurs
c) Neither event occurs
d) Exactly one event occur
Answers
a) Both events occur: A ∩ B
b) At least one event occurs: A ∪ B
c) Neither event occurs: A' ∩ B'
d) Exactly one event occurs: (A ∩ B') ∪ (A' ∩ B)
In Event A and B, the intersection A ∩ B tells us the outcome where both events occur. The Union of A and B tells us the outcome where at least one event occurs. The intersection of the complements of A and B (A' ∩ B') tells us the outcome where neither event occurs.
Finally, the union of the intersection of A and the complement of B and the intersection of the complement of A and B ( (A ∩ B') ∪ (A' ∩ B) ) tells us the outcome where exactly one event occurs.
Read more about Set theory:
https://brainly.com/question/2166579
#SPJ4
scatter plot- construct a scatter plot.

Answers
The Constructed scatter plot matches option A
How to construct a scatter plot?A scatter plot is a type of plot or mathematical diagram using Cartesian coordinates to display values for typically two variables for a set of data
Given: The x and y values as shown in the question
X| 0.1 | 0.1 | 0.1 | 0.2 | 0.5 | 1 |
Y| 0.86 | 0.87 | 0.88 | 0.81 | 0.56 | 0.2 |
The values of X against Y will then be plotted on a scatter plot as shown in the image attached. Note that X values will be on the horizontal while Y values will be on the vertical.
Looking at the attached scatter plot, the scatter plot in option A is the one matches it. Therefore, option A is the answer.
Learn more about scatter plot on:
https://brainly.com/question/16920148
#SPJ1
