Please help me with this quickly, the question says show your work or explain but I just need the explanation, thank you!!
Answers
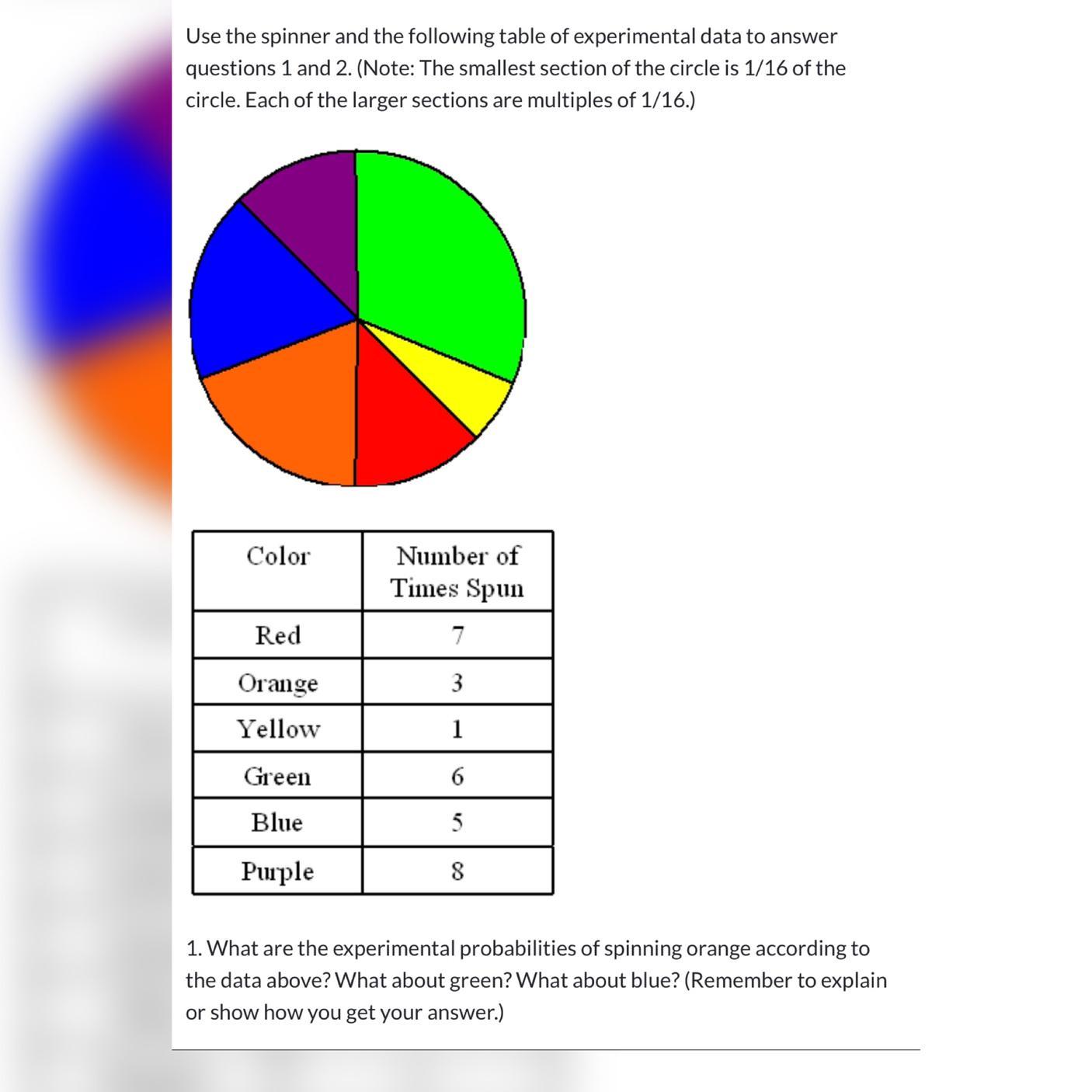
The experimental probabilities of spinning orange according to the data above: P(orange, yellow)= 1/8, P(green, blue, purple)= 5/8,P(red, orange, yellow, green, blue, purple) =1.
P(red, yellow, blue)= 6/16= 3/8.
4/16+ 1/16+ 1/16= 6/16= 3/8
P(orange, yellow)= 1/8
1/16+1/16= 2/16= 1/8
P(green, blue, purple)= 5/8
7/16+1/16+2/16= 10/16= 5/8.
P(pink)=0
There is no pink color.
P(red, orange, yellow, green, blue, purple)?
P(red, orange, yellow, green, blue, purple)= 16/16= 1.
4/16+ 1/16+ 1/16+ 7/16+1/16+2/16 =16/16= 1.
To learn more about probabilities visit:https://brainly.com/question/11234923
#SPJ9
Related Questions
What is the area of the rhombus? 11 m2 15 m2 22 m2 44 m2

Answers
Answer:
44 m2
Step-by-step explanation:
The area of the rhombus can be divided into 4 equal triangles.
The area of one triangle is A=bh/2
so:
A = 5.5*2
A = 11 squared m
Since there are four (4) triangles in the rhombus we just need to multiply 11 by 4 so:
A = 11 * 4
A = 44 squared m
I WILL GIVE BRAINERLEST ABD LIKE AND 5 STARS IF YOU ANSWER
How many people n would be seated in
each section if there were 27 total
people in the gym?
Answers
Answer:
IT SAYS IT 27 PEOPLE WOULD BE SEATED
Step-by-step explanation:
Find the sales tax.
Sales Tax
Selling Price Rate of Sales Tax Sales Tax
$20.00
5%
?
The sales tax is $.
This is due tomorrow!please help :)
Answers
Answer:
$1.00
Step-by-step explanation:
20.00 dollars x 5% =1.00
Answer:
$1.00
Step-by-step explanation:
Sales price ($20) x tax rate (.05) = $1.00
1+Sin/Cos + Cos/1+Sin = 2Sec

Answers
Step-by-step explanation:
Consider the left-hand side:
\(\dfrac{1+\sin{\theta}}{\cos{\theta}} + \dfrac{\cos{\theta}}{1+\sin{\theta}}\)
\(\:\:\:\:= \dfrac{(1+\sin{\theta})^2 + \cos^2{\theta}}{\cos{\theta}(1+\sin{\theta})}\)
\(\:\:\:\:=\dfrac{1+2\sin{\theta}+\sin^2{\theta} + \cos^2{\theta}}{\cos{\theta}(1+\sin{\theta})}\)
\(\:\:\:\:=\dfrac{2+2\sin{\theta}}{\cos{\theta}(1+\sin{\theta})} =\dfrac{2(1+\sin{\theta})}{\cos{\theta}(1+\sin{\theta})}\)
\(\:\:\:\:= \dfrac{2}{\cos{\theta}} = 2\sec{\theta}\)
the current in the electronic circuit in the mobile phone was 0.12a the potential difference across the battery was 3.9V. calculate the resistance of the electronic circuit in the mobile phone
Answers
Answer:
Step-by-step explanation:
V = 3.9V
I = 0.12A
Ohm's Law, V = IR
Rearranging Ohm's Law, R = V/I
R = 3.9/0.12 = 32.5Ω
Urgenteee
Un tronco de madera de 3,080 kg de 1m de diametro
y 10m de largo, flota en el agua ¿Cuanto es el volumen de tronco
por arriba de la superficie del agua?
Answers
The volume of the log will be 30,70,760 m³.
What is Archimedes principle?Mathematically, we can write Archimedes principle as -
F{buoyant} = - fluid density {ρ} x acceleration due to gravity {g} x volume {v}
Given is that a 3080 kg log of wood with a diameter of 1 m and 10 m long, it floats in the water.
Since the log floats on water, the density of both the log and water is same.
So, we can write volume as -
Volume = 3080 x 997 Volume = 30,70,760 m³
Therefore, the volume of the log will be 30,70,760 m³.
To solve more questions on Archimedes principle, visit the link below
https://brainly.com/question/787619
#SPJ9
{QUESTION IN ENGLISH -urgent A 3,080 kg log of wood with a diameter of 1 m and 10 m long, it floats in the water. What is the volume of the trunk above the surface of the water?}
I need help with this, can anybody help me? thank you, have. a great day!

Answers
Answer:a
Step-by-step explanation:
Answer:
As a mixed number, it is 3 5/8.
As an improper fraction it is 29/8.
Hope that helps you. x
introduces a husband and wife with brown eyes who have 0.75 probability of having children with brown eyes, 0.125 probability of having children with blue eyes, and 0.125 probability of having children with green eyes. a) What is the probability that their first child will have green eyes and the second will not? b) What is the probability that exactly one of their two children will have green eyes? c) If they have six children, what is the probability that exactly two will have green eyes? d) If they have six children, what is the probability that at least one will have green eyes? e) What is the probability that the first green eyed child will be the 4th child? f) Would it be considered unusual if only 2 out of their 6 children had brown eyes?
Answers
The probability of their first child having green eyes is 0.125, and the probability of their second child not having them is 0.875.
What is a probability?Probability is an estimate of how likely an occurrence is to occur. It's a figure between 0 and 1, where 0 means the event is unlikely and 1 means the event is certain. A likelihood of 0.5 (or 50%) indicates that the occurrence has an equal chance of occurring or not occurring.
In the given question,
a) The probability of their first child having green eyes is 0.125. The probability of their second child not having green eyes is 1 - 0.125 = 0.875. Therefore, the probability that their first child will have green eyes and the second will not is 0.125 x 0.875 = 0.1094.
b) The probability of exactly one of their two children having green eyes can be calculated in two ways: either the first child has green eyes and the second doesn't, or the first child doesn't have green eyes and the second does. The probability of the first scenario was calculated in part (a) to be 0.1094, and the probability of the second scenario is the same, so the total probability is 2 x 0.1094 = 0.2188.
c) The probability of exactly two out of six children having green eyes can be calculated using the binomial distribution with n = 6, p = 0.125, and k = 2. The formula for this probability is:
P(k=2) = (6 choose 2) x \(0.125^2 x (1 - 0.125)^4\) = 0.1936
where (6 choose 2) = 6!/(2!4!) = 15 is the number of ways to choose 2 children out of 6.
d) The probability of at least one of their six children having green eyes is the complement of the probability that none of them do. The probability that any one child doesn't have green eyes is 1 - 0.125 = 0.875, so the probability that none of the six children have green eyes is \(0.875^6\) = 0.1779. Therefore, the probability that at least one of their six children has green eyes is 1 - 0.1779 = 0.8221.
e) The probability that the first green-eyed child will be the fourth child is the probability that the first three children do not have green eyes, multiplied by the probability that the fourth child has green eyes, multiplied by the probability that the fifth and sixth children do not have green eyes. The first three children have a probability of \((1-0.125)^3\) = 0.578 to not have green eyes. The fourth child has a probability of 0.125 to have green eyes. The probability that the fifth and sixth children do not have green eyes is \((1-0.125)^2\) = 0.765625. Therefore, the probability that the first green-eyed child will be the fourth child is 0.578 x 0.125 x 0.765625 = 0.0557.
f) It would depend on the context and the specific definition of "unusual." If the expected number of brown-eyed children is 0.75 x 6 = 4.5, then having only 2 out of 6 children with brown eyes is below average. However, the probability of this exact outcome can be calculated using the binomial distribution with n = 6 and p = 0.75:
P(k=2) = (6 choose 2) x \(0.75^2 x (1 - 0.75)^4\) = 0.0986
where (6 choose 2) = 6!/(2!4!) = 15 is the number of ways to choose 2 children out of 6. This probability is not very low (less than 10%), so it might not be considered unusual in a statistical sense.
To know more about probability, visit
brainly.com/question/14210034
#SPJ1
11 of 3011 of 30 Questions
Question
A baker makes peanut butter cookies and chocolate chip cookies.
She needs 2 cups of flour and 34
cup of butter to make one batch of peanut butter cookies.
She needs 3 cups of flour and 1 cup of butter to make one batch of chocolate chip cookies.
If the baker has 26 cups of flour and 9 cups of butter, how many batches of each type of cookie can she make?
Answers
The baker can only make peanut butter cookies and cannot make any chocolate chip cookies with the given amount of ingredients.
Let's denote the number of batches of peanut butter cookies as "x" and the number of batches of chocolate chip cookies as "y."
From the given information, we can set up the following system of equations:
For the flour:
2x + 3y = 26
For the butter:
34x + y = 9
To solve this system of equations, we can use the substitution method or the elimination method. Let's use the elimination method:
Multiply the first equation by 17 (to make the coefficients of x in both equations the same):
34x + 51y = 442
Now we have the system of equations:
34x + y = 9
34x + 51y = 442
Subtract the first equation from the second equation:
34x + 51y - (34x + y) = 442 - 9
50y = 433
Divide both sides by 50:
y = 433/50
Since the number of batches of cookies cannot be fractional, we need to find a whole number solution for y. However, in this case, y is a fraction, indicating that the given amount of butter is not sufficient to make even one batch of chocolate chip cookies.
for similar questions on ingredients.
https://brainly.com/question/1578467
#SPJ8
Write the expression without using exponents.
(−9x)4
Answers
The expression (-9x)^4 can be represented as -6561x^3 without using exponents.
To express the expression (-9x)^4 without using exponents, we can expand it by multiplying the base (-9x) four times using the multiplication property.
(-9x)^4 = (-9x) * (-9x) * (-9x) * (-9x)
To simplify this expression, we can multiply the terms together, taking care to apply the rules of multiplication:
(-9x) * (-9x) = (-9 * -9) * (x * x) = 81 * x^2 = 81x^2
So, by substituting this result back into the original expression, we get:
(-9x)^4 = 81x^2 * (-9x) = -6561 x^3
Therefore, the expression (-9x)^4 can be represented as -6561x^3 without using exponents.
for such more question on exponents
https://brainly.com/question/4077992
#SPJ8
I’LL GIVE BRAINLIEST, A HEART, AND 5 STARS TO WHOEVER ANSWERS FIRST
(Please answer ALL questions and show how you got the answer!)

Answers
Group B has lower range.
Group A shows variability.
Mean is the best to make concussion about age of Salsa students.
Upon visual examination, it appears that Group A is likely to have a lower average age of music students compared to Group B.
This inference is supported by the observation that the majority of data points in Group B are concentrated around younger ages.
In contrast, Group A exhibits a more dispersed distribution of data points across a wider range of ages, including higher.
So, Group B has lower range.
and, Group A shows variability.
Lastly, Mean is the best to make concussion about age of Salsa students.
Learn more about dot plot here:
brainly.com/question/32312452
#SPJ1
A rectangular prism has a width of x2 inches and a length of xy2 inches and a height of xy inches.
Which expression represents the volume of the rectangular prism in cubic inches?
2x^2y^2
2xy^3 + 2x^2y
2x^4y^3
x^3y^2
Answers
In this case, the width is x^2 inches, the length is xy^2 inches, and the height is xy inches.
Substituting these values into the formula, we get:
V = (xy^2)(x^2)(xy)
Simplifying, we get:
V = x^4y^3
Therefore, the expression that represents the volume of the rectangular prism in cubic inches is x^4y^3.
Help me with this math question please

Answers
Answer:
60 small and 140 large = 60 + 280 = 340 this is correct!
Step-by-step explanation:
I guess we just use the process of eleimation.
50 small and 150 Large = 50+300 = 350 so that's not right.
130 small and 70 large = 130 + 140 = 270 so, that's not right.
120 small and 80 large = 120 + 160 = 280 so, that's not right.
60 small and 140 large = 60 + 280 = 340 this is correct!
Solve each system of linear equations below, then check your work.
A. 3x−y=−11 −x+y=5
B -2y+3= 4x + 2 6x + 4y=1
C. 32y- x= -25 5x= 100 + x - 8Y
D. 2y + 3x = 6 4x + 5y +20 = 0
Answers
A. The solution of linear equation is (x, y) = (-3, 8).
B. The solution is (x, y) = (3/4, -1).
C. The solution is (x, y) = (-31/8, 3/8).
D. The solution is (x, y) = (55/7, -117/14).
A. 3x - y = -11 --- (1)
-x + y = 5 --- (2)
From equation (2), we can write y = x + 5, and substitute it in equation (1):
3x - (x + 5) = -11
2x = -6
x = -3
Substituting x in equation (2):
-y = -8
y = 8
Therefore, the solution of the system is (x, y) = (-3, 8).
To check the solution, we substitute the values of x and y in the original equations:
3(-3) - 8 = -11 (True)
-(-3) + 8 = 5 (True)
So, the solution is correct.
B. -2y + 3 = 4x + 2 --- (1)
6x + 4y = 1 --- (2)
From equation (1), we can write 4x + 2 = -2y + 3, and substitute it in equation (2):
6x + 4y = 1
6x - 4y = 8 (rearranging)
12x = 9
x = 3/4
Substituting x in equation (1):
-2y + 3 = 4(3/4) + 2
-2y + 3 = 5
-2y = 2
y = -1
Therefore, the solution of the system is (x, y) = (3/4, -1).
To check the solution, we substitute the values of x and y in the original equations:
-2(-1) + 3 = 4(3/4) + 2 (True)
6(3/4) + 4(-1) = 1 (True)
So, the solution is correct.
C. 32y - x = -25 --- (1)
5x = 100 + x - 8y --- (2)
From equation (2), we can write 4x = 100 - 8y, and substitute it in equation (1):
32y - x = -25
32y - (100 - 8y) = -25
40y = 75
y = 3/8
Substituting y in equation (1):
32(3/8) - x = -25
x = -31/8.
Therefore, the solution of the system is (x, y) = (-31/8, 3/8).
To check the solution, we substitute the values of x and y in the original equations:
32(3/8) - (-31/8) = -25 (True)
5(-31/8) = 100 + (-31/8) - 8(3/8) (True)
So, the solution is correct.
D. To solve the system of equations:
2y + 3x = 6 --- (1)
4x + 5y + 20 = 0 --- (2)
We can rearrange equation (2) to isolate one of the variables:
4x + 5y = -20 (subtracting 20 from both sides)
5y = -4x - 20 (subtracting 4x from both sides)
y = (-4/5)x - 4 (dividing both sides by 5)
Substituting this value of y in equation (1):
2((-4/5)x - 4) + 3x = 6
(-8/5)x - 8 + 3x = 6
(-8/5)x + 3x = 14
(-8/5 + 3)x = 14
(-8/5 + 15/5)x = 14
(7/5)x = 14
x = 10
Substituting this value of x in the equation for y:
y = (-4/5)(10) - 4
y = -12.
Therefore, the solution of the system is (x, y) = (10, -12).
To check the solution, we substitute the values of x and y in the original equations:
2(-12) + 3(10) = 6 (True)
4(10) + 5(-12) + 20 = 0 (True)
So, the solution is correct.
For similar question on linear equations.
https://brainly.com/question/2030026
#SPJ11
1.3 x 10 to the power of negative 3
Answers
Answer:0.0013
Step-by-step explanation:
Answer: the answer is on the calclulator
Step-by-step explanation:
What the meaning of "f is order-preserving if x < y implies f(x) < f(y)"?

Answers
An order-preserving function is a function that preserves the order of its inputs. In other words, if x is less than y, then f(x) will be less than f(y).
The statement "f is order-preserving if x < y implies f(x) < f(y)" means that if x is less than y, then f(x) must be less than f(y). This is a necessary condition for a function to be order-preserving. However, it is not a sufficient condition. For example, the function f(x) = x^2 is not order-preserving, because 2 < 3, but f(2) = 4 > f(3) = 9.
In summary, order-preserving functions are useful in situations where we need to preserve the order of a set of data.
Learn more on functions:https://brainly.com/question/11624077
#SPJ1
The conditional statement below is true. If possible, write the biconditional statement.
If 2x = 18, then x = 9.
Answers
The biconditional statement for the given conditional statement would be:
2x = 18 if and only if x = 9.
The given conditional statement "If 2x = 18, then x = 9" can be represented symbolically as p → q, where p represents the statement "2x = 18" and q represents the statement "x = 9".
To form the biconditional statement, we need to determine if the converse of the conditional statement is also true. The converse of the original statement is "If x = 9, then 2x = 18". Let's evaluate the converse statement.
If x = 9, then substituting this value into the equation 2x = 18 gives us 2(9) = 18, which is indeed true. Therefore, the converse of the original statement is true.
Based on this, we can write the biconditional statement:
2x = 18 if and only if x = 9.
The biconditional statement implies that if 2x is equal to 18, then x must be equal to 9, and conversely, if x is equal to 9, then 2x is equal to 18. The biconditional statement asserts the equivalence between the two statements, indicating that they always hold true together.
In summary, the biconditional statement is a concise way of expressing that 2x = 18 if and only if x = 9, capturing the mutual implication between the two statements.
for such more question on conditional statement
https://brainly.com/question/27839142
#SPJ8
To what power do you have to raise:
a) 3 to get 27?
to
b) 2 to get 32?
CO
c) 5 to get 625?
d) 64 to get 8?
e) 81 to get 3?
f) 64 to get 2?
g) x² to get x??
h) x to get x12?
10
i) x to get xa?

Answers
Answer:
Step-by-step explanation:
a) 27 = 3 × 3 × 3 = 3³ Answer: 3
b) 32 = 2 × 2 × 2 × 2 × 2 = \(2^5\) Answer: 5
c) 625 = 5 × 5 × 5 × 5 = \(5^4\) Answer: 4
d) \(\sqrt{64} = 8 \) ⇒ \(64^{\frac{1}{2}} \) Answer: 1/2
e) \(\sqrt[4]{81}=3 \) ⇒ \(81^{\frac{1}{4}} \) Answer: 1/4
f) \(\sqrt[6]{64} =2\) ⇒ \(64^{\frac{1}{6} }\) Answer: 1/6
g) \((x^2)^{\frac{1}{2}}=x^1=x \) Answer: 1/2
h) \((x^3)^{4}=x^{12}\) Answer: 4
i) \((x)^8=x^8\) Answer: 8
Answer:
Step-by-step explanation:
Prime factorize 27,32,625,
a) 27 = 3 * 3 * 3 = 3³
b) 32 = 2 * 2 * 2 * 2 *2 = 2⁵
c) 625 = 5*5*5*5 = 5⁴
\(d) \sqrt{64}= (8^{2})^{\frac{1}{2}} = 8\\\\ e) \sqrt[4]{81}=\sqrt[4]{3*3*3*3}=(3^{4})^{\frac{1}{4}} = 3\\\\ f) \sqrt[6]{64}=\sqrt[6]{2*2*2*2*2*2}=(2^{6})^{\frac{1}{6}}=2\\\\ g)\sqrt{x^{2}}=(x^{2})^{\frac{1}{2}}=x\\\\ \)
\(h) x^{12} = x^{3*4}= (x^{3})^{4}\\\\ i)x^{8}=x^{1*8}=(x^{1})^{8}\)
Find the area of a rectangle whose length is 14cm and breadth is 6cm

Answers
Answer:
Ellos dan las pistas de algunos problemas se pueden resolver de forma automática, los valores numéricos tienen ninguna importancia en los distintos ejemplos.
Traza 1
Uno de los lados de un rectángulo es 20 cm de largo; un segundo lado del rectángulo es de 0,85 m de largo. Calcular el perímetro y el área del rectángulo.
Traza 2
Calcular el área de un rectángulo cuyas dimensiones son 85 cm de largo y 20 cm respectivamente.
Traza 3
La base de un rectángulo es 20 cm de largo; la área es de 300 cm². Calcular la altura del rectángulo.
Traza 4
La altura de un rectángulo es 15 cm de largo; la área es de 300 cm². Calcula la base del rectángulo.
Traza 5
Un rectángulo tiene la altura que es de 3/8 de la base; la suma de las longitudes de los dos segmentos es 44 cm. Determinar el área del rectángulo y el perímetro.
Traza 6
La base de un rectángulo es de 0,40 m de largo; La altura del rectángulo es 30 cm. Calcular la diagonal.
Traza 7
Un tamaño de un rectángulo es un medio del lado de un cuadrado que tiene el perímetro de 20 cm. Sabiendo que los dos polígonos tienen el mismo perímetro, calcula la medida del tamaño del rectángulo.
Traza 8
La diagonal de un rectángulo es de 50 cm; la base es de 3/4 de la altura. Calcular el perímetro y el área del rectángulo.
Traza 9
La diagonal de un rectángulo mide 50 cm; ella es 5/3 de altura. Calcular el perímetro y el área del rectángulo.
Traza 10
Una mesa rectangular tiene lados de 180 cm y 90 cm respectivamente. Cuál es el perímetro y el área de un mantel que cuelga de 20 cm alrededor de la mesa?
Traza 11
Calcular el área de un rectángulo que tiene la altura 10 cm de largo, sabiendo que la medida de la base es el doble de la altura.
Traza 12
La diferencia entre el tamaño de un rectángulo es 12 cm y una es el triple de la otra. Calcular el área del rectángulo
Traza 13
La suma entre el tamaño de un rectángulo es 12 cm y una es el triple de la otra. Calcular el área del rectángulo
Traza 14
La suma de la base y la altura de un rectángulo es 50 cm; la base es superior a la altura de 4 cm. Calcular el área del rectángulo.
Traza 15
El semi-perímetro de un rectángulo es 32 cm y una dimensión es de 3/5 de la otra. Calcular el área del rectángulo.
Traza 16
El semi-perímetro de un rectángulo es 30 cm y una dimensión es igual a los sus 2/5. Calcular el área del rectángulo.
Traza 17
Un rectángulo tiene una base de 20 cm y una altura igual a 2/5 de la base. Calcular el perímetro y el área del rectángulo.
Traza 18
Un rectángulo tiene el área de 600 cm² y la base es 20 cm de largo. Cuál es su perímetro ?
Traza 19
Un rectángulo tiene un perímetro de 100 cm y la base es 30 cm de largo. Calcula su área.
Traza 20
Un rectángulo tiene un perímetro de 120 cm. Sabiendo que un tamaño es tres veces la otra, calcula el área del rectángulo.
Traza 21
La diferencia entre el tamaño de un rectángulo es 10 dm. Sabiendo que el perímetro es 100 dm, calcula el área del rectángulo.
Traza 22
Un rectángulo tiene un perímetro de 100 cm. Calcula su área sabiendo que la medida de la base es superior a la de la altura de 10 cm.
Traza 23
En el perímetro de un rectángulo es de 100 cm y la altura es de 20 cm de largo. Calcular el perímetro de un rectángulo equivalente a el mismo y que tiene su base de 40 cm de largo.
Traza 24
Un rectángulo es formado por dos cuadrados congruentes que tienen cada uno el perímetro de 24 cm. Calcular el perímetro y el área del rectángulo.
Traza 25
Un rectángulo es formado por tres cuadrados congruentes con cada lado 20 cm de largo. Calcular el perímetro y el área del rectángulo.
Traza 26
Un rectángulo es formado por dos cuadrados congruentes. Sabiendo que el perímetro del rectángulo es de 180 cm, calcular su área.
Traza 27
Un rectángulo y un cuadrado tienen el mismo perímetro. El lado de un cuadrado de 45 cm y las dimensiones del rectángulo son una 1/2 de la otra. Calcular el área del rectángulo.
Traza 28
Dos rectángulos son equivalentes. Sabiendo que las dimensiones de el primero miden respectivamente 30 cm y 20 cm, y que la base del segundo rectángulo es 40 cm de largo, calcula la diferencia entre los dos perímetros.
Traza 29
Calcular el perímetro de la figura y el área de la parte interior con la obtención de las medidas a partir del dibujo:
Traza 30
Calcular el perímetro de la figura y el área de la parte interior con la obtención de las medidas a partir del dibujo:
Traza 31
Un constructor ha comprado un terreno que tiene la planta mostrada en el dibujo y las dimensiones en metros se indican en la figura. Calcula el área y el perímetro de la tierra.
Traza 32
Una parcela de tierra tiene una forma rectangular con unas dimensiones de 50 m y de 30 m de largo. En el interior se ha construido una casa que ocupa una superficie rectangular de longitud 20 m y de 8 m de ancho. Calcular el área de la tierra permanecida libre.
Traza 33
Step-by-step explanation:
Answer:
A= 84cm
Step-by-step explanation:
length x width= area
plug in the given information.
14cm x 6cm = A
A=84
with a length of 14cm and a width of 6cm multiply them for an area of 84cm.
(f) 0.7 - 6.32 + (-0.8) + 1.28
Answers
Answer:
=0.7f−5.84
Step-by-step explanation:
Let's simplify step-by-step.
f(0.7)−6.32−0.8+1.28
=0.7f+−6.32+−0.8+1.28
Combine Like Terms:
=0.7f+−6.32+−0.8+1.28
=(0.7f)+(−6.32+−0.8+1.28)
=0.7f+−5.84
Answer:
=0.7f−5.84
Pls Brainliest
if bob and billy went on a date, and had kids even though it is not biologically possible, what is the distance between the sun from john and paul's baby?
please i need a lot of help
Answers
Answer:
who's john?
Step-by-step explanation:
Answer:
B
Step-by-step explanation:
Because A GAY couple can adopt or its hypothetical that they can have a baby obviously
I need help with this

Answers
The option that can be used to verify the trigonometric identity, \(tan\left(\dfrac{x}{2}\right)+cot\left(x \right) = csc\left(x \right)\) is option C;
C. \(tan\left(\dfrac{x}{2} \right) + cot\left(x \right) = \dfrac{1-cos\left(x \right)}{sin\left( x \right)} +\dfrac{cos \left(x \right)}{sin\left(x \right)} =csc\left(x \right)\)
What is a trigonometric identity?A trigonometric identity is an equations that consists of trigonometric functions that remain true for all values of the argument of the functions
The specified identity is presented as follows;
\(tan\left(\dfrac{x}{2} \right)+cot(x)=csc(x)\)
The half angle formula for tangent indicates that we get;
\(tan\left(\dfrac{1}{2} \cdot \left(\eta \pm \theta \right) \right) = \dfrac{tan\left(\dfrac{1}{2} \cdot \eta \right)\pm tan\left(\dfrac{1}{2} \cdot \theta \right)}{1 \mp tan\left(\dfrac{1}{2} \cdot \eta \right)\times tan\left(\dfrac{1}{2} \cdot \theta \right)}\)
\(\dfrac{tan\left(\dfrac{1}{2} \cdot \eta \right)\pm tan\left(\dfrac{1}{2} \cdot \theta \right)}{1 \mp tan\left(\dfrac{1}{2} \cdot \eta \right)\times tan\left(\dfrac{1}{2} \cdot \theta \right)}=\dfrac{sin \left(\eta\right) \pm sin\left(\theta \right)}{cos \left(\eta \right) + cos \left(\theta \right)} = -\dfrac{cos \left(\eta\right) - cos\left(\theta \right)}{sin \left(\eta \right) \mp sin \left(\theta \right)}\)
When η = 0, we get;
\(-\dfrac{cos \left(0\right) - cos\left(\theta \right)}{sin \left(0 \right) \mp sin \left(\theta \right)}=-\dfrac{1 - cos\left(\theta \right)}{0 \mp sin \left(\theta \right)}=\dfrac{1 - cos\left(\theta \right)}{sin \left(\theta \right)}\)
Therefore;
\(tan\left(\dfrac{x}{2} \right)=\dfrac{1 - cos\left(x \right)}{sin \left(x \right)}\)
\(cot\left(x \right) = \dfrac{cos(x)}{sin(x)}\)
\(tan\left(\dfrac{x}{2} \right)+cot(x)= \dfrac{1 - cos\left(x \right)}{sin \left(x \right)} +\dfrac{cos(x)}{sin(x)}\)
\(\dfrac{1 - cos\left(x \right)}{sin \left(x \right)} +\dfrac{cos(x)}{sin(x)}=\dfrac{1-cos(x)+cos(x)}{sin(x)} = \dfrac{1}{sin(x)}\)
\(\dfrac{1 - cos\left(x \right)}{sin \left(x \right)} +\dfrac{cos(x)}{sin(x)}=\dfrac{1}{sin(x)}=csc(x)\)
Therefore;
\(tan\left(\dfrac{x}{2} \right)+cot(x)= \dfrac{1 - cos\left(x \right)}{sin \left(x \right)} +\dfrac{cos(x)}{sin(x)} = csc(x)\)
The correct option that can be used to verify the identity is option C
Learn more about trigonometric identities in mathematics here:
https://brainly.com/question/14421002
#SPJ1
Question Determine the geometric mean of 54 and 18. Round your answer to then nearest tenths place ifnecessary.
Answers
We have the following:
\(x=\sqrt[n]{x_1\cdot x_2\ldots x_n}\)replacing:
\(\begin{gathered} x=\sqrt[2]{54\cdot18} \\ x=\sqrt[2]{972} \\ x=18\sqrt[]{3}=31.18 \end{gathered}\)the geometric mean of 54 and 18 is 31.18
Differentiate the function h() = (2 + 1)5 tan
Answers
The value of the function when differentiated w.r.t "x" is -2 / 1+x^2.
To differentite the function \(f(x) = tan^{-1}(\frac{1-x}{1+x}) - tan^{-1}(\frac{x+2}{1-2x})\) w.r.t "x", we have to make use of chain rule and the derivative of the inverse tangent function. By applying both the methods, we have to find out the differentiated value of the function.
Chain rule is basically a fundamental rule in calculus that allows us to find the derivative of a function. The chain rule comes out to be very usefull when the functions are layered. On the other hand, inverse tangent function is a mathematical function that takes an input value and returns the angle whose tangent is equal to that value.
We know that;
\(tan^{-1}a - tan^{-1}b = tan^{-1}(\frac{a-b}{1+ab} )\)
So, by following the above method we get the function as:
\(f(x) = (tan^{-1}1 - tan^{-1}x) - (tan^{-1}x + tan^{-1}2)\)
\(f(x) = tan^{-1}1 - tan^{-1}2 - 2tan^{-1}x\)
Now, differentiating both the sides w.r.t "x":
f'(x) = 0 - 0 - 2/1+x^2
f'(x) = 2/1+x^2
Therefore, the value of the function when differentiated w.r.t "x" is
-2 / 1+x^2.
To study more about Chain rule:
https://brainly.com/question/30895266
I NEED THE ANSWER ASAP
If you were to write the slope-intercept equation for a line that goes through the point (4,-3)--with a slope of -2--what would be the value of b?
y=mx+b
Answers
y=-2x+5 is the slope-intercept equation for a line that goes through the point (4,-3) and 5 is the value of b.
What is Slope of Line?The slope of the line is the ratio of the rise to the run, or rise divided by the run. It describes the steepness of line in the coordinate plane.
The slope intercept form of a line is y=mx+b, where m is slope and b is the y intercept.
The slope of line passing through two points (x₁, y₁) and (x₂, y₂) is
m=y₂-y₁/x₂-x₁
We have to find the slope-intercept equation for a line that goes through the point (4,-3)--with a slope of -2
m=-2
Now let us find the y intercept
-3=-2(4)+b
-3=-8+b
-3+8=b
5=b
Hence, y=-2x+5 is the slope-intercept equation for a line that goes through the point (4,-3) and 5 is the value of b.
To learn more on slope of line click:
https://brainly.com/question/14511992
#SPJ1
HELP ME IM TOTALLY LOST AND HAVE A HARD TIME ASKING PEOPLE FOR HELP

Answers
Answer:
a. 1,323,002
Step-by-step explanation:
Martin a une table ronde de 1 ,10m de diamètre il peut ajouter jusqu'à 5 rallonge de 40 cm chacune pour son repas d'anniversaire 10 personne seront présentes autour de cette table En comptant 60 cm par personne quel est le nombre minimal de rallonge qu'il doit installé

Answers
C = π x 1,10 m ≈ 3,46 m
Sachant que chaque rallonge mesure 40 cm (soit 0,4 m), le nombre minimal de rallonges que Martin doit installer est :
(nombre de personnes x largeur par personne - diamètre de la table) / longueur d'une rallonge
= (10 x 0,60 m - 1,10 m) / 0,40 m
= (6 m - 1,10 m) / 0,40 m
= 14,75
Comme il ne peut pas installer une demi-rallonge, il doit donc installer au moins 15 rallonges pour que tout le monde puisse s'asseoir confortablement autour de la table.
4
(Graphing Proportional Relationships LC)
The table shows a proportional relationship.
x 12 8 24
y 3 26
Describe what the graph of the proportional relationship would look like.
O Aline passes through the point (0, 0) and continues through the point (3, 12).
O Aline passes through the point (0, 0) and continues through the point (2,8).
A line passes through the point (0, 0) and continues through the point (6, 24).
A line passes through the point (0, 0) and continues through the point (12, 3).
Question 2(Multiple Choice Worth 2 points)
(Graphing Proportional Relationships MG)
Answers
The correct answer is option D: A line passes through the point (0, 0) and continues through the point (12, 3)
For the first question:
The table shows a proportional relationship between x and y. To describe what the graph of this proportional relationship would look like, we can examine the given data points.
The data points are (12, 3), (8, 26), and (24, ?). We can observe that as x increases, y also increases. This indicates a positive correlation between the variables. Additionally, we can see that the ratio of y to x remains constant for each data point.
Now, let's analyze the answer options:
A. A line passes through the point (0, 0) and continues through the point (3, 12).
This answer option does not align with the given data because there is no data point with an x-value of 3 and a corresponding y-value of 12.
B. A line passes through the point (0, 0) and continues through the point (2, 8).
This answer option aligns with the given data because (2, 8) is a valid data point from the table, and the line passes through the origin (0, 0).
C. A line passes through the point (0, 0) and continues through the point (6, 24).
This answer option does not align with the given data because there is no data point with an x-value of 6 and a corresponding y-value of 24.
D. A line passes through the point (0, 0) and continues through the point (12, 3).
This answer option aligns with the given data because (12, 3) is a valid data point from the table, and the line passes through the origin (0, 0).
Based on the analysis, the correct answer is option D: A line passes through the point (0, 0) and continues through the point (12, 3). This accurately represents the graph of the proportional relationship given in the table.
For the second question, I'm sorry, but you didn't provide the multiple-choice options or the complete question. Could you please provide the question and options so that I can assist you further?
for more such question on point visit
https://brainly.com/question/1859113
#SPJ8
What do you add to 4 4/9 to make 8
Answers
You need to add 3 5/9 to make 8. If you want to know what 4 4/9 goes to, to make 8, do the opposite which is subtracting. 8 turn to 7 9/9 and then subtract 4 4/9 and then you get the answer aka 3 5/9.
Please anwser this is all the points I have :)

Answers
Check the picture below.
so let's recall that the area of a circle is just πr² where r = radius, so since the sizes of each pizza are 10, 14, 18 and 22, that's simply their diameter, so that means they each have a radius half of that, or namely 5, 7, 9 and 11, as you see in the picture, so, hmmm which radius gives us the most area per the fraction provided, namely per slices provided?
\(\cfrac{4}{8}\pi 5^2\implies \cfrac{25\pi }{2} ~~ \approx ~~ 39.26~in^2 \\\\[-0.35em] ~\dotfill\\\\ \cfrac{3}{8}\pi 7^2\implies \cfrac{147\pi }{8} ~~ \approx ~~ 57.73~in^2 \\\\[-0.35em] ~\dotfill\\\\ \cfrac{2}{8}\pi 9^2\implies \cfrac{81\pi }{4}~~ \approx ~~ 63.62~in^2 ~~ \textit{\LARGE \checkmark} \\\\[-0.35em] ~\dotfill\\\\ \cfrac{1}{8}\pi 11^2\implies \cfrac{121\pi }{8}~~ \approx ~~ 47.52~in^2\)

Answer: Large
Step-by-step explanation: Hope it helps Good luck!!!