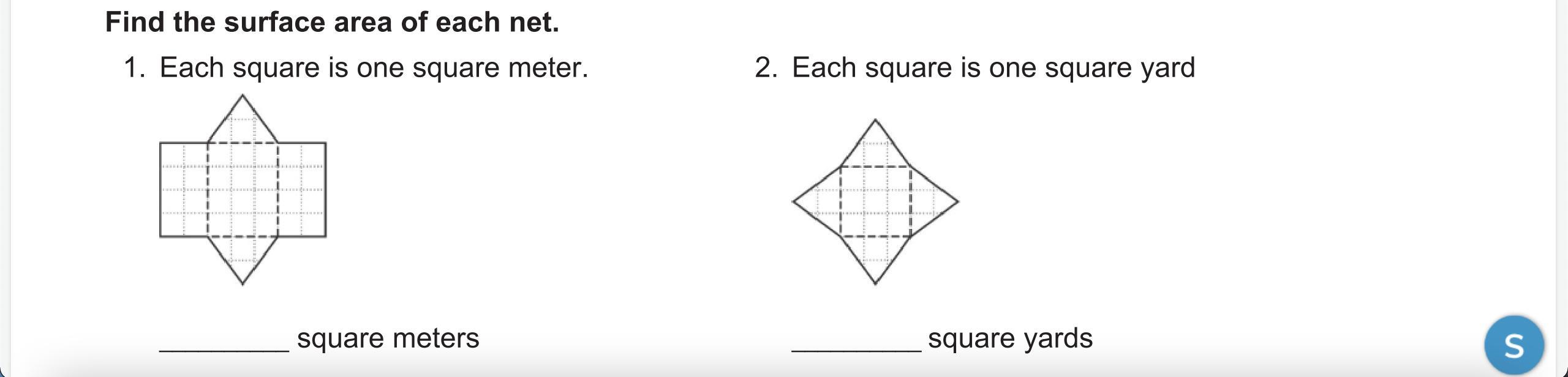
Answers
Answer:
1) 30
2) 13
Step-by-step explanation:
I could be wrong but i counted all of the full squares in the shape
Related Questions
Which expression is equivalent to (7x + 6) - (4x + 2)?
Answers
Answer:
=(3x+4)
Step-by-step explanation:
Answer:
What r the options, I’ll help when u show the options
Step-by-step explanation:
Use the Pythagorean theorem to solve for x

Answers
Answer: 15
Step-by-step explanation:
12^2 + 9^2 = 225
square root of 225 = 15
what is x-6>6 . solve for x
Answers
Answer:
x>12
Step-by-step explanation:
x-6>6
move constant (6) to right
x>6+6
x>12
alternate form
(12, infinity symbol)
hope this helps
Answer:
12
Step-by-step explanation:
At a coffee shop, the amount of tax due is calculated based on the cost of the customer's
order.
t = the amount of tax due
c = the cost of the order
Which of the variables is independent and which is dependent?
Answers
In this context, the dependent variable is t (amount of tax due) and the independent variable is c (cost of the order).In this scenario, the variables are t (the amount of tax due) and c (the cost of the order).
To determine which variable is independent and which is dependent, we need to understand their relationship.In this case, the amount of tax due, t, is calculated based on the cost of the customer's order, c. The tax amount is dependent on the cost of the order because it is directly influenced by the value of c. As the cost of the order changes, the amount of tax due will also change accordingly.
On the other hand, the cost of the order, c, is independent. It is not influenced or determined by the amount of tax due. The customer can choose the cost of their order, and the tax will be calculated based on that chosen amount.
For more such questions on variable
https://brainly.com/question/27894163
#SPJ8
a spherical balloon is inflated so that its volume is increasing at the rate of 3.7 ft3/min. how rapidly is the diameter of the balloon increasing when the diameter is 1.5 feet?
Answers
Using Sphere geometry formulas , 2.45 ft/min is increasing rate of spherical ballon when the diameter is 1.5 feet.
Sphere is a three dimensional form of circle .
let V and D be volume and diameter of the sphere. we have given that ,
Volume increasing rate of spherical ballon (dV/dt)
= 3.7 ft³/min
diameter of sphere at time of increasing = 1.5 feet
the increasing rate of spherical ballon is dD/dt.
Now, Volume of sphere (V) = 4/3π³ ft³
or we know that D = r/2 so,
V = 4/3 π (D)³×8 ft³
differentating both sides we get ,
dV/dt = 32/8π 3D³dD/dt
=> 3.7 = 32/3 (3.14)(1.5)²dD/dt
=> dD/dt= 2.45 feet/min
Hence, 2.45 ft/min is the rate of the diameter of the balloon increasing when the diameter is 1.5 feet.
To learn more about Sphere geometry , refer:
https://brainly.com/question/4515545
#SPJ4
What is the hydrogen ion concentration
of orange juice that has a pH of 1?
0.1 mole per liter
0.01 mole per liter
0.0001 mole per liter
0.00001 mole per liter
Answers
Answer:
0.1 mole per liter
Step-by-step explanation:
i got it right
I need help immediately!!!

Answers
The limit as x approaches one is infinity.
\(lim_{x\to1}\frac{x + x {}^{2} + {x}^{3} + ... + {x}^{100} - 1000}{1 - x} =\infty\)
What is the limit of a function?The limit of a function, f(x) as x approaches a given value b, is define as the value that the function f(x) attains as the variable x approaches the given value b.
From the given question, as x approaches 1,
substituting x into 1 - x,
the denominator of the function approaches zero, because 1 - 1 = 0 and thus the function becomes more and more arbitrarily large.
Thus, the limit of the function as x approaches 1 is infinity.
Therefore,
The limit (as x approaches 1)
\(lim_{x\to1}\frac{x + x {}^{2} + {x}^{3} + ... + {x}^{100} - 1000}{1 - x} = \infty \)
Learn more about limits of a function here:
https://brainly.com/question/2393546
#SPJ1
An algorithm will be used to calculate the difference between the smallest and largest values in a list. For the list of [10, 3, 5, 6], it should calculate a difference of 7.
There are two proposals for the algorithm:
Algorithm 1: Set minVal to the first value in the list and maxVal to the last value in the list. Iterate through each number in the list. If the number is greater than maxVal, store it in maxVal. If the number is less than minVal, store it in minVal. After loop, set maxDiff to the difference between maxVal and minVal.
Algorithm 2: Set minVal to 1000 and maxVal to 0. Iterate through each number in the list. If the number is greater than maxVal, store it in maxVal. If the number is less than minVal, store it in minVal. After loop, set maxDiff to the difference between maxVal and minVal.
Which of these statements are true about these algorithms?
I. Algorithm 1 does not work on lists where the smallest value is at the start of the list or the largest value is at the end of the list.
II. Algorithm 2 does not work on lists that contain all negative numbers or all numbers over 1000.
Answers
The statements that are true about the given algorithms are: I. Algorithm 1 does not work on lists where the smallest value is at the start of the list or the largest value is at the end of the list. II. Algorithm 2 does not work on lists that contain all negative numbers or all numbers over 1000.
Algorithm 1's reliance on initializing minVal to the first value and maxVal to the last value can lead to incorrect results if the smallest or largest value is not properly updated during the iteration. Similarly, Algorithm 2's fixed initial values for minVal and maxVal can result in incorrect differences when dealing with lists containing all negative numbers or all numbers over 1000.
It is important to consider these limitations and potential failure cases when choosing and implementing an algorithm for calculating the difference between the smallest and largest values in a list.
Learn more about Algorithm here:
https://brainly.com/question/30753708
#SPJ11
please helpp me !!!!!



Answers
1. define your variables. your variables can be anything you want, but I will use x and y. x=adult tickets; y=child tickets
2. Now, you need 2 equations. For the first equation you will use the facts you are given about money. Adult ticket costs 9 dollars, each child ticket costs 5 , and Mary spent $110. Make these facts into an equation using the variables you have defined
3. Now make an equation using the facts you are given about the number of tickets sold and bought. You don’t know how many of each ticket she bought, so you just use your variables to make an equation using the fact that Mary bought 14 tickets.
4. Now, you have two different equations. You can solve by substitution or elimination, either will work, however I prefer elimination. Put the equations on top of each other, and eliminate one of the variables. Find the value of the variable you did not eliminate, and substitute that into one of your original equations that you created in step 2 or 3. It doesn’t matter which one you substitute into. Now, you will have found the values of x and y. Remember, x is the number of adult tickets, and y is the number of child tickets.
I hope this helps!
At the neighborhood grocery, 55 pounds of steak cost $36.50. How much would it cost to buy 3.93.9 pounds of steak?
Answers
The amount it would cost to buy 3.9 pounds of steak is $2.59
Calculating the cost it would take to buy steakFrom the question, we are to determine how much it would cost to buy 3.9 pounds of steak
Let the cost be $x
From the given information, we have that
55 pounds of steak cost $36.50
If 55 pounds of steak cost $36.50
Then,
3.9 pounds of steak will cost $x
Thus,
55 × x = 3.9 × 36.50
55x = 142.35
x = 142.35/55
x = 2.588
x ≈ 2.59
Hence, the cost is $2.59
Learn more on Calculating cost here: https://brainly.com/question/5168855
#SPJ1
find a div m and a mod m when a) a = 228, m = 119. b) a = 9009, m = 223. c) a = −10101, m = 333. d) a = −765432, m = 38271.
Answers
To find the divisor (div) and the remainder (mod):
a) To find div and mod, we use the formula: a = m x div + mod.
For a=228 and m=119:
- div = floor(a/m) = floor(1.9244) = 1
- mod = a - m x div = 228 - 119 x 1 = 109
Therefore, div = 1 and mod = 109.
b) For a=9009 and m=223:
- div = floor(a/m) = floor(40.4469) = 40
- mod = a - m x div = 9009 - 223 x 40 = 49
Therefore, div = 40 and mod = 49.
c) For a=-10101 and m=333:
- div = floor(a/m) = floor(-30.3903) = -31
- mod = a - m x div = -10101 - 333 x (-31) = -18
Therefore, div = -31 and mod = -18.
d) For a=-765432 and m=38271:
- div = floor(a/m) = floor(-19.9885) = -20
- mod = a - m x div = -765432 - 38271 x (-20) = -2932
Therefore, div = -20 and mod = -2932.
Learn more about mod: https://brainly.com/question/30544434
#SPJ11
is (, ) = 3 − 32 an harmonic function? if yes, then find a corresponding analytic function ()
Answers
No, f(x, y) = 3x - 3y^2 is not a harmonic function.
A harmonic function is a twice continuously differentiable function f(x, y) that satisfies the Laplace equation:
∂²f/∂x² + ∂²f/∂y² = 0.
Let's check if f(x, y) = 3x - 3y^2 satisfies the Laplace equation:
∂²f/∂x² = ∂/∂x(3) = 0
∂²f/∂y² = ∂/∂y(-6y) = -6
∂²f/∂x² + ∂²f/∂y² = 0 + (-6) = -6 ≠ 0
Since the Laplace equation is not satisfied, f(x, y) = 3x - 3y^2 is not a harmonic function.
As for finding a corresponding analytic function, an analytic function is a function that is locally given by a convergent power series. Since f(x, y) is not a harmonic function, there is no corresponding analytic function.
Read more about harmonic functions at:
https://brainly.com/question/30385079
#SPJ11
The number of pennies in a jar of coins is 4 more than 5 times the number of dimes in the jar Let p = the number of pennies in the jar. Let d = the number of dimes in the jar. Which equation represents this situation?
Answers
The equation that represents this situation is p = 4 + 5d
What are algebraic expressions?Algebraic expressions are known as mathematical expressions made up of:
VariablesConstants AdditionSubtractionMultiplicationSome other algebraic operationsFrom the information given, we have that:
p is the number of pennies in the jard is the number of dimes in the jarThe number of pennies in a jar of coins is 4 more than 5 times the number of dimes in the jarThe equation this represents is:
p = 4 + 5d
Thus, the equation that represents this situation is p = 4 + 5d
Learn more about algebraic expressions here:
https://brainly.com/question/4344214
#SPJ1
On a number line, point d is at -6, and point e is at 8. point f lies between points d and e. if is , where does point f lie on the number line? point f is at on the number line.
Answers
The point F lies on 4.5 in the number line.
What is the number line?
The number line is a One dimensional representation of point referring by a number only.
We know that if a point divides a line joining the points at x, y in the number line respectively in m:n ratio then that point lies on
= (my+nx)/(m+n) in the number line.
Here in the given problem that,
Point D lies on -6 in the number lin
Point E lies on 8 in the number line
And F lies between D and E points and DE:EF = 3:1
So the point F clearly divides the staright line DE joining the point D at -6 and E at 8 in 3:1 ratio.
So the point F lies on = (1*(-6)+3*8)/(3+1) = (-6+24)/4 = 18/4 = 4.5
Hence, the point F lies on 4.5 in the number line.
To learn more about the Number Line visit,
brainly.com/question/4727909
#SPJ4
The rule T⟨4, −1⟩ is used on the preimage point (2, −7). What is the image point?
Answers
The image point for the given rule and preimage is (6 - 8)
What is the image point?When we apply a rule T<a, b> to a preimage point (x, y) we get the image (x + a, y + b), so this is like a translation.
So if we apply the rule T<4, -1> to the preimage point (2, -7), the image will be:
(2 + 4, - 7 + (-1)) = (6 - 8)
Concluding, the image point is (6 - 8)
If you want to learn more about translations, you can read:
https://brainly.com/question/2972832
4. Recursively defined sets ( 3 points) Give a recursive definition of the set below. The set of positive integer powers of 5 . 5. Divisibility (4 points) Prove that if a∣b and b∣a, then a=b or a=−b.
Answers
4. We start with the base case of \(5^0 = 1\) and recursively generate the next element in the set by multiplying the previous element by \(5\).
5. if a divides \(b\) and \(b\) divides \(a\), either a equals \(b\) or \(a\) equals negative \(b\).
4. The recursive definition of the set of positive integer powers of 5 can be expressed as follows:
Base case: \(5^0 = 1\) is in the set.
Recursive step: If n is in the set, then \(5^(n+1)\) is also in the set.
Using this definition, we start with the base case of \(5^0 = 1\)and recursively generate the next element in the set by multiplying the previous element by \(5\).
5. To prove that if a divides \(b\) and \(b\)divides \(a\), then a equals \(b\) or \(a\) equals negative \(b\), we can use the definition of divisibility.
Assume that \(a\) divides \(b\), denoted as \(a | b\) , and \(b\) divides \(a\), denoted as \(b | a.\)
By definition, if a divides b, there exists an integer k such that b = ak.
Similarly, if \(b\) divides \(a\), there exists an integer m such that \(a = bm.\)
Substituting the expression for\(b\) in terms of \(a\), we have \(bm = ak.\)
Dividing both sides by b (since b is nonzero), we get m = a/b.
Since \(m\) is an integer, \(a/b\) must be an integer, which means \(a\) is divisible by \(b\).
If \(a/b\) is an integer, it implies that \(b/a\)is also an integer, which means \(b\) is divisible by \(a\).
Therefore, if \(a\) divides \(b\) and \(b\) divides \(a\), it follows that \(a/b\) and \(b/a\) are both integers.
If \(a/b = m\) and \(b/a = k\), then we have \(a = bm\) and\(b = ak.\)
\(If m = k = 1, then $a = b.\)
\(If m = k = -1, then a = -b.\)
Therefore, if \(a\) divides \(b\) and \(b\) divides \(a\), either \(a\) equals \(b\) or \(a\) equals negative \(b\).
Learn more about Recursion
https://brainly.com/question/31387281
#SPJ11
If a straight path in the park is 900 feet long, how long would the path be when represented on the map?
Do not include units (inches) in your answer.
Answers
Answer:
The path indicated by long green dashes on an ordnance map
refers to a walking path that is a public right of way.
Step-by-step explanation:
The length of the path on the map would be 4.5 inches.
Here, we have to find the length of the path on the map, we can use the scale provided: 1 inch represents 200 feet.
If the actual length of the path in the park is 900 feet, we can set up a proportion to find the corresponding length on the map.
Let x be the length of the path on the map (in inches).
Proportion: (Actual Length) / (Length on Map) = (Scale Factor)
900 feet / x inches = 200 feet / 1 inch
Now, solve for x:
x = (900 feet * 1 inch) / 200 feet
x = 900 / 200
x = 4.5
So, the length of the path on the map would be 4.5 inches.
To learn more on scale factor click:
brainly.com/question/5992872
#SPJ3
complete question:
A local park is in the shape of a square. A map of the local park is made with the scale 1 inch to 200 feet.
If a straight path in the park is 900 feet long, how long would the path be when represented on the map?
Do not include units (inches) in your answer.
the maclaurin series for the function f(x) is given by the formula x [infinity] n=1 (−1)n 1 x n 3n2 (n 5). the value of f (5)(0) (the 5-th derivative of f evaluated at x = 0) is A)-4/25 B)4/25 C)-1/750 D)1/750
Answers
The value of f(5)(0) for the given Maclaurin series is -1/750.
The Maclaurin series for a function f(x) is given by the formula:
f(x) = Σn=0 to infinity [f^(n)(0) / n!] x^n
where f^(n)(0) is the nth derivative of f evaluated at x=0.
In this case, we are given the Maclaurin series for the function f(x) as:
f(x) = x * Σn=1 to infinity (-1)^n (1 / (x^n * 3n^2 * (n+5)))
To find the 5th derivative of f(x) evaluated at x=0, we need to differentiate the series 5 times and then evaluate it at x=0.
f(1)(x) = Σn=1 to infinity (-1)^n (1 / (x^(n-1) * 3n^2 * (n+5)))
f(2)(x) = Σn=1 to infinity (-1)^n * (n-1) / (x^n * 3n^2 * (n+5))
f(3)(x) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) / (x^(n+1) * 3n^2 * (n+5))
f(4)(x) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) / (x^(n+2) * 3n^2 * (n+5))
f(5)(x) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) * (n+12) / (x^(n+3) * 3n^2 * (n+5))
Substituting x=0, we get:
f(5)(0) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) * (n+12) / (0^(n+3) * 3n^2 * (n+5))
Simplifying the denominator, we get:
f(5)(0) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) * (n+12) / (3n^2 * (n+5))
To evaluate this series, we can use partial fraction decomposition and then use the formula for the sum of the series 1/n^2.
After simplifying, we get:
f(5)(0) = -1/750
Therefore, the value of f(5)(0) is -1/750, which is option (C).
Learn more about Maclaurin series here
https://brainly.com/question/28170689
#SPJ11
.
The sum of two numbers is 10. Triple the first number and double the second number and their sum is 30. Find the value of the two numbers
Answers
Answer:
x = 10, y = 0
Step-by-step explanation:
x + y = 10 ---> x = 10 - y
3x + 2y = 30
3 (10 - y) + 2y = 30
30 - 3y + 2y = 30
y = 0
x + 0 = 10
x = 10
I NEED THE ANSWER TO THIS ASAP PLEASE!!!
what is 1/25 of 5.2 time 10 to the power of 3?
Answers
Answer:
208
Step-by-step explanation:
Answer:8
Step-by-step explanation:
helppp due in 21 mins

Answers
Answer:
Step-by-step explanation:
19. 12960
20. 6000
How to find this? Please help me.

Answers
Answer:
b = 9 cm
Step-by-step explanation:
the area (A) of a triangle is calculated as
A = \(\frac{1}{2}\) bh ( b is the base and h the height )
here h = 2b , then
\(\frac{1}{2}\) × b × 2b = 81
\(\frac{1}{2}\) × 2b² = 81
b² = 81 ( take square root of both sides )
b = \(\sqrt{81}\) = 9 cm
a snack manufacturer finds that it must increase the salt content of its chips by 8 percent in order for a sample of consumers to notice that the chips are saltier than they were before (baseline). this example most nearly illustrates the concept of a( n ):
Answers
A threshold effect is when a small change in one variable results in a noticeable change in another variable. In this example, a small 8% increase in salt content of the chips is enough to produce a noticeable change in the saltiness of the chips to the sample of consumers.
The snack manufacturer can calculate the increase in salt content of their chips needed to produce the threshold effect by first determining the baseline salt content of the chips. Once this is known, they can then calculate what percentage increase to the salt content is needed by multiplying the baseline salt content by 8%. For example, if the baseline salt content of the chips is 10%, then the 8% increase in salt content would be calculated as 10% x 8% = 0.8%. This means that the snack manufacturer needs to increase the salt content of their chips by 0.8% to reach the threshold effect desired by the sample of consumers.
Learn more about variable here
https://brainly.com/question/29583350
#SPJ4
Suppose you are going to test the hypothesis that population 1 has a mean that is exactly 2 less than the mean of population 2. Sample 1 has a mean of 34. 5 and sample 2 has a mean of 30. The respective standard deviations are 5 and 9 and the sample sizes are 33 and 42. What is the test statistic?.
Answers
To test the hypothesis that population 1 has a mean that is exactly 2 less than the mean of population 2, we can use a two-sample t-test with unequal variances.
The test statistic for this hypothesis is given by:
t = (x1 - x2 - d) / sqrt[(s1^2/n1) + (s2^2/n2)]
where x1 and x2 are the sample means, s1 and s2 are the respective standard deviations, n1 and n2 are the sample sizes, and d is the hypothesized difference in means (in this case, d = 2).
Substituting the given values, we get:
t = (34.5 - 30 - 2) / sqrt[(5^2/33) + (9^2/42)]
t = 2.5 / 1.747
t = 1.43 (rounded to two decimal places)
Therefore, the test statistic for this hypothesis is 1.43.
You want to test the hypothesis that the mean of population 1 is exactly 2 less than the mean of population 2. Given that sample 1 has a mean of 34.5 and sample 2 has a mean of 30, the respective standard deviations are 5 and 9, and the sample sizes are 33 and 42. To find the test statistic, follow these steps:
1. State the null hypothesis (H0) and the alternative hypothesis (H1):
H0: μ1 - μ2 = 2
H1: μ1 - μ2 ≠ 2
2. Calculate the difference in sample means (M1 - M2):
34.5 - 30 = 4.5
3. Calculate the standard error of the difference in means:
SE = √[(s1²/n1) + (s2²/n2)] = √[(5²/33) + (9²/42)] = √[(25/33) + (81/42)] ≈ 1.595
4. Calculate the test statistic (t):
t = (M1 - M2 - D) / SE = (4.5 - 2) / 1.595 ≈ 1.568
The test statistic for this hypothesis test is approximately 1.568.
Visit here to learn more about standard deviations:
brainly.com/question/23907081
#SPJ11
A bag holds 2 red and 7 blue marbles. What is the probability of the complement of randomly selecting a red marble? Please help asap
Answers
Answer:
I'll help the best I can lol
Step-by-step explanation:
You have a 2 in 9 chance randomly selecting a red marble, so your probability of selecting one in the first place.
2/9 chance is 81.8% impaled probability.
Help ASAP I’ll mark you as brainlister

Answers

what is -8 divided 6.4. ??
Answers
Answer:
-1.25
Step-by-step explanation:
When -8 is divided by 6.4 we get -1.25.
Use the concept of division defined as:
Repetitive subtraction is the process of division. It is the multiplication operation's opposite. It is described as the process of creating equitable groupings. When dividing numbers, we divide a bigger number down into smaller ones such that the larger number obtained will be equal to the multiplication of the smaller numbers.
Here we have to find the number when,
-8 divided by 6.4
It can be written as,
-8/6.4
Multiply and divide 10 on both the numerator and denominator,
-80/64
Now divide 80 by 64 then attach the negative sign in the quotient.
The division is attached below.
Hence,
The required number is -1.25.
To learn more about division visit:
https://brainly.com/question/2273245
#SPJ3

what are the four conditions necessary for x to have a binomial distribution? mark all that apply.
Answers
Characteristic of binomial distribution Mean should be n *p n is the number of trials p is the successful outcome of the process
a set number of trials, such as three rolls of the dice or five flips of the coin.Each trial can either be successful or unsuccessful. Note that the example with the die seems to have six possible outcomes. We must take into account options like "get a 6" (success) or "not obtain a 6." (failure).The likelihood of success must be constant (equal for every try). P(6) = 1/6 for each roll of the die in the example.The trials are separate. The likelihood of success in future trials is unaffected by the outcome of the first.Know more about binomial at:
https://brainly.com/question/9325204
#SPJ4
ASAP answer please it mathematics

Answers
Answer: D
Step-by-step explanation:
First, we see that each flower basket is the variable x. This is because that is what increases per situation. The constant fee no matter the amount of flower baskets for store A is $15, so for store A our equation is
Total spent=19.25x+15
And similarly, for store B it is
Total spent=17.50x+30
Now, to compare them we want to keep store A LESS THAN (<) store B ,
so we get that 19.25x+15<17.50+30, which is D
write an equation of the line in point slope form that passes through the given points (3,4) and (4,6)An equation of the line is??
Answers
re The point-slope form of a line is
\(y-y_1=m(x-x_1)\)The slope m of the line passing through these two points is the difference between their y coordinates divided by the difference between their x - coordinate.
\(m=\frac{6-4}{4-3}\)\(m=2\)Now we need only find the y-intercept.
Let us use the point (3, 4) which tells us that at x = 3, y = 4; therefore,
\(4-y_1=2(3)\)\(y_1=-2\)Hence, the question of our line in point-slope form is
\(\textcolor{#FF7968}{y+2=2x}\)Alternatively, when we have the slope of the line we would just use one of the points to quickly write the point-intercept form.
The y_1 and x_1 in the very first equation are the coordinates of one of the points on the line =. We know that one of the point on our line is (3, 4);