solve with explanation
2(12)-(-4)
Answers
Answer:
28
Step-by-step explanation:
2×12-(-4) - and - = +
24+4 + and + = +
28 + and - = -
- and + = -
Related Questions
I need help asap, giving 30 points and brainiest!

Answers
The sum of angles of a linear pair is always equal to 180°.
7x + 12 + 8x + 3 = 180
Simplify
15x + 15 = 180
-15
15x = 165
/15
x = 11
Answer = x = 11
Have a good day ^^
Answer:
\(x=11\)
Step-by-step explanation:
It is a linear pair
\(7x + 12 + 8x + 3 = 180\)
\(15x + 15 = 180-15\\15x = 165\)
\(x=11\)
In the National AIDS Behavioral Surveys sample of 2673 adult heterosexuals, 0.2% (that's 0.002 as a proportion) had both received a blood transfusion and had a sexual partner from a group at high risk of AIDS. Explain why we can't use the large-sample confidence interval to estimate the proportion, p, in the population who share these two risk factors.
a. Large-sample confidence intervals should never be used when the sample proportion is smaller than 0.05.
b. There should be no problem using the large-sample confidence interval since the sample size was so large.
c. There should be no problem since the sample was random.
d. We can't assume that the sampling distribution of ^
p
is approximately Normal because n(p?) < 10.
Answers
As per the concept of confidence interval the risk factors are
a. Large-sample confidence intervals should never be used when the sample proportion is smaller than 0.05.
d. We can't assume that the sampling distribution of ^p is approximately Normal because n(p) < 10.
Confidence intervals are a range of values that provide a measure of how confident we are about our estimate of a population parameter.
Now, let's consider the National AIDS Behavioral Surveys sample of 2673 adult heterosexuals. We want to estimate the proportion of the population who have both received a blood transfusion and have a sexual partner from a group at high risk of AIDS.
The sample proportion is 0.2% (0.002 as a proportion). However, we can't use the large-sample confidence interval to estimate the population proportion for several reasons.
Firstly, it's not a rule that we can't use large-sample confidence intervals when the sample proportion is smaller than 0.05. The 0.05 threshold is often used as a guideline, but it's not a strict rule.
Secondly, while the sample size is large, with 2673 observations, this doesn't necessarily mean we can use a large-sample confidence interval. We need to check whether certain assumptions hold, such as the sample being random and independent, and the sample size being large enough.
Finally, the main reason why we can't use the large-sample confidence interval is that the assumption of a Normal sampling distribution doesn't hold. This assumption is necessary for constructing a large-sample confidence interval.
In particular, we can't assume that the sampling distribution of the sample proportion (^p) is approximately Normal because the product n*p is less than 10. This means that the sample size is not large enough to guarantee a Normal distribution.
To know more about confidence interval here.
https://brainly.com/question/24131141
#SPJ4
Help now please... I will mark brainlest

Answers
Answer:
60°
Step-by-step explanation:
That's an equilateral triangle therefore all sides and angles are the same.
find the smallest number by which 1372 must be multiplied so that the product is a perfect cube
Answers
5 Vera is a shop manager. 5 She has this information about the income in her shop for eight weeks this year. Week 1 2. 3 4 5 6 7 8 Income (thousands of £) 53.5 42.3 39.8 45.1 52.4 19.4 47.9 42.5 The median income for the same eight weeks last year was £49 300 Vera knows that the median income for these eight weeks has decreased this year compared to last year. (a) Work out the percentage decrease of the median income. Give your answer to 2 decimal places.
Answers
Using the median concept, it is found that it suffered a 11.16% decrease.
What is the median of a data-set?It is the 50th percentile of the data-set, which is the value that separates the lower 50% from the upper 50%.
In this problem, the ordered data-set, in thousands of £, is given by:
{19.4, 39.8, 42.3, 42.5, 45.1, 47.9, 52.4, 53.5}
It has even cardinality, hence the median is the mean of the 8/2 = 4th and 5th terms, so:
M = (42.5 + 45.1)/2 = £43800.
It decreased from £49300 last year. The percentage decrease is the change divided by initial amount and multiplied by 100%, hence:
P = (49300 - 43800)/49300 x 100% = 11.16%.
More can be learned about the median concept at https://brainly.com/question/25215461
6 - 8x = 6x - 9x + 11
Answers
6-8x=-3x+11
-8x+3x=11-6
-5x=5
x=-1
The first step is to isolate the variable, then you solve. Hope this helps, brainliest if you can.
Answer:
hi
Step-by-step explanation:
hi i am a gamergirl add me in fortnite xxgamergilxx93_qt
when does two plus two equal five
Answers
An examination paper has 150 multiple-choice questions of one mark each, with each question having four choices. Each incorrect answer fetches -0.25 mark. Suppose 1000 students choose all their answers randomly with uniform probability. The sum total of the expected marks obtained by all these students is?
Answers
The sum of expected marks is given as follows:
9375.
How to obtain the expected marks?Each question has four choices, hence the probability of choosing the correct choice is given as follows:
p = 1/4 = 0.25.
Then the expected number of correct answers is given as follows:
E(X) = 0.25 x 150
E(X) = 37.5.
Then the expected grade for a single student is given as follows:
37.5 - 0.25(150 - 37.5) = 9.375.
The expected sum for the 1000 students is then given as follows:
1000 x 9.375 = 9375.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
Is the range a subset or a proper subset of the codomain?
Answers
A function's codomain is a subset of its range. Although it is not a true subset, it is conceivable for the range to be equal to the codomain, in which case it is also a subset of the codomain.
What is a subset?A set that includes all or a portion of another set's elements is known as a subset. For instance, because every even integer is also an integer, the set of even integers is a subset of the set of integers. A subset that contains some, but not all, of the members of another set is said to be a proper subset. Because it contains some, but not all, of the positive integers, the set of positive integers less than 10 is a valid subset of the set of positive integers.
A function's codomain is a subset of its range. Although it is not a true subset, it is conceivable for the range to be equal to the codomain, in which case it is also a subset of the codomain.
Learn more about subset here:
https://brainly.com/question/24138395
#SPJ1
John ran up and $88 Bill last Saturday the service was excellent so we decided to leave a 30% tip for the waitress how much was his tip
Answers
$26.40
ten percent is 88 divided by 10= 8.8
8.8 multiplied by 3 is 26.40
Jim ate two slices of pizza, which is 25% of the pizza. How many slices were in the whole pizza?Sonya buys a baseball jersey for her brother on sale for 20% off. If the price she paid was $6 lower than the regular price, what was the original price of the jersey
Answers
There were 8 slices in the whole pizza.
How many slices were in the whole pizza if Jim ate two slices?An equation means the formula that expresses the equality of two expressions by connecting them with the equals sign =. Let us assume the number of slices in the whole pizza is "x".
Since Jim ate two slices which is 25% of the pizza, we will set up the equation:
2 = 0.25x
To solve for "x":
2 / 0.25 = x
x = 8.
Read more about equation
brainly.com/question/29174899
#SPJ1
Find the greatest common factor (GCF) of 14 and 12.
Answers
Equation in standard form using the given points

Answers
standard form for a linear equation means
• all coefficients must be integers, no fractions
• only the constant on the right-hand-side
• all variables on the left-hand-side, sorted
• "x" must not have a negative coefficient
now, to get the equation of any straight line, we simply need two points off of it, let's use those two in the picture below.
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{6})\qquad (\stackrel{x_2}{-3}~,~\stackrel{y_2}{2}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{2}-\stackrel{y1}{6}}}{\underset{run} {\underset{x_2}{-3}-\underset{x_1}{(-6)}}} \implies \cfrac{-4}{-3 +6} \implies \cfrac{ -4 }{ 3 } \implies - \cfrac{4 }{ 3 }\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{6}=\stackrel{m}{- \cfrac{4 }{ 3 }}(x-\stackrel{x_1}{(-6)}) \implies y -6 = - \cfrac{4 }{ 3 } ( x +6) \\\\\\ \stackrel{\textit{multiplying both sides by}\stackrel{LCD}{3}}{3(y-6)=3\left( - \cfrac{4 }{ 3 } ( x +6) \right)} \implies 3y-18=-4(x+6) \\\\\\ 3y-18=-4x-24\implies 3y=-4x-6\implies {\Large \begin{array}{llll} 4x+3y=-6 \end{array}}\)

Joe makes an hourly wage of $14.00. Last week, Joe worked 58 hours.
What is Joe's gross pay for this pay period?
Answers
Answer:
812 dollars 14 x 58 = $812 dollars.
Step-by-step explanation:
Answer:
I think it is 812 tell me if I'm wrong please
Shoe City is offering 15% discount on all pairs of shoes. If u also have an extra 20% off coupon, how much would a pair of shoes that are originally $68 cost after the discounts?
Answers
Answer:
The shoes would cost $46.24
Step-by-step explanation:
68 x 0.15 = 10.2
68 - 10.2 = 57.8
57.8 x 0.20 = 11.56
57.8 - 11.56 = 46.24
Write the equation of the line that is perpendicular to 3x+2y=8 and goes through the point (-5,2)
Answers
Answer:
\(\displaystyle y=\frac{2}{3}(x+5)+2\)
Step-by-step explanation:
We need to find the equation of the line perpendicular to the line 3x+2y=8 and passes through (-5,2).
The given line can be expressed as:
\(\displaystyle y=-\frac{3}{2}x+4\)
We can see the slope of this line is m1=-3/2.
The slopes of two perpendicular lines, say m1 and m2, meet the condition:
\(m_1.m_2=-1\)
Solving for m2:
\(\displaystyle m_2=-\frac{1}{m_1}\)
\(\displaystyle m_2=-\frac{1}{-\frac{3}{2}}\)
\(\displaystyle m_2=\frac{2}{3}\)
Now we know the slope of the new line, we use the slope-point form of the line:
\(y=m(x-h)+k\)
Where m is the slope and (h,k) is the point. Using the provided point (-5,2):
\(\boxed{\displaystyle y=\frac{2}{3}(x+5)+2}\)
Samples of a cast aluminum part are classified on the basis of surface finish (in microinches) and edge finish. The results of 102 parts are summarized as follows: edge finish excellent good surface finish excellent 84 4 good 5 9 Let A denote the event that a sample has excellent surface finish, and let B denote the event that a sample has excellent edge finish. If a part is selected at random, determine the following probabilities. Round your answers to three decimal places (e.g. 98.765). (a) Upper P left-parenthesis Upper A right-parenthesis equalsEntry field with correct answer .8627 (b) Upper P left-parenthesis Upper B right-parenthesis equalsEntry field with correct answer .8725 (c) Upper P left-parenthesis Upper A prime right-parenthesis equalsEntry field with correct answer .1372 (d) Upper P left-parenthesis Upper A intersection Upper B right-parenthesis equalsEntry field with correct answer .8235 (e) Upper P left-parenthesis Upper A union Upper B right-parenthesis equalsEntry field with correct answer .9117 (f) Upper P left-parenthesis Upper A prime union Upper B right-parenthesis equalsEntry field with incorrect answer .9214
Answers
Answer:
a) P (A)= 88/102= 0.8627
(b) P (B)= 89/102= 0.8725
c) P (A`) = 14/102 = 0.1372
(d) P (A∩B) = 84/102 =0.8235
(e) P(AUB)= 93/102 = 0.9117
(f)P (A`UB) = 98/102= 0.96078
Step-by-step explanation:
edge
finish excellent good Total
(A )surface finish excellent 84 4 88
good ( B) ⇵ 5 9 14
Total 89 13 102
a) Upper P left-parenthesis Upper A right-parenthesis equals
P (A)= 88/102= 0.8627
All the elements of set A = 84+4= 88
(b) Upper P left-parenthesis Upper B right-parenthesis equals
P (B)= 89/102= 0.8725
All the elements of set B = 84+5= 89
c) Upper P left-parenthesis Upper A prime right-parenthesis equal
P (A`) = 14/102 = 0.1372
All the elements of Universal set U which are not elements of set A = 102- 88= 14
(d) Upper P left-parenthesis Upper A intersection Upper B right-parenthesis equals
P (A∩B) = 84/102 =0.8235
Only those elements of set A and set B which are common
(e) Upper P left-parenthesis Upper A union Upper B right-parenthesis equals
P(AUB)= 93/102 = 0.9117
Totalling elements of set A and B= 88+5= 93
(f) Upper P left-parenthesis Upper A prime union Upper B right-parenthesis equals
P (A`UB) = 98/102= 0.96078
All the elements of Universal set U which are not elements of set A and the elements of Set B = 5+9+ 84= 98
A. John wants to find the average time it takes students to run a lap around the track. He will consider 24 students to find the average time. Which unit(s) could be used for the unit of measurement?
1. Pounds
2. Seconds
3. Ounces
4. Minutes
5. Grams
B. Which of the procedures below would be the best way to find the average time?
1. Ask for 24 volunteers to run a lap around the track and have them state their own times.
2. Measure the times of 24 volunteers who run a lap around the track.
3. Randomly pick 24 students to run a lap around the track and measure their times.
4. Randomly pick 24 students to run a lap around the track and have them state their own times.
Answers
Answer:
A) 2. Seconds
4. Minutes
B) 2. Measure the times of 24 volunteers who run a lap around the track.
3. Randomly pick 24 students to run a lap around the track and measure their times.
Step-by-step explanation:
A. The unit(s) that could be used for the unit of measurement are the units used to measure time and the correct answer according to the options given above is seconds and minutes.
B. Which of the procedures below would be the best way to find the average time?
2. Measure the times of 24 volunteers who run a lap around the track.
3. Randomly pick 24 students to run a lap around the track and measure their times.
If a rock is thrown upward on the planet Mars with a velocity 16 m/s, its height in meters t seconds later is given by y = 16t − 1.86t2. (Round your answers to two decimal places.)
(a)Find the average velocity (in m/s) over the given time intervals:
A. [1,2]
B. [1,1.5]
C. [1,1.1]
D. [1,1.01]
E. [1,1.001]
Answers
The average velocity (in m/s) over the given time intervals is [1,2]
Part A.
Keep in mind that the formula for average velocity is
(Y2 - Y1)/V avg = displacement/time interval (t2 - t1)
Given that the rock's position at time t is determined by:
y = 16t - 1.86*t^2
Part 1
for the time period [1, 2]
Y1 = 16*1 - 1.86*12 = 14.14 m when t1 = 1 sec.
Y2 = 16*2 - 1.86*22 = 24.56 m when t2 = 2 sec.
So
average Velocity = (24.56 - 14.14)/(2 - 1) (2 - 1) = 10.42 m/s V avg
Part 2.
for the time period [1, 2]
Y1 = 16*1 - 1.86*12 = 14.14 m when t1 = 1 sec.
Y2 = 16*1.5 - 1.86*1.52 = 19.815 m when t2 = 1.5 sec.
So,
average Velocity = (19.815 - 14.14)/(1.5 - 1) (1.5 - 1) = 11.35 m/s V avg
Part 3.
During the period [1, 1] .1]
Y1 = 16*1 - 1.86*12 = 14.14 m when t1 = 1 sec.
Y2 = 16*1.1 - 1.86*1.12 = 15.3494 m when t2 = 1.1 sec.
So,
average Velocity = (15.3494 - 14.14)/(1.1 - 1) (1.1 - 1)
average Velocity = 12.094 m/s and equals 12.09 m/s (In two decimal places)
Part 4.
During the period [1, 1] .01]
Y1 = 16*1 - 1.86*12 = 14.14 m when t1 = 1 sec.
Y2 = 16*1.01 - 1.86*1.012 = 14.262614 m when t2 = 1.01 sec.
So,
average Velocity = (14.262614 - 14.14)/(1.01 - 1) (1.01 - 1)
12.26 m/s and V avg = 12.2614 m/s (In two decimal places)
Part 5.
During the period [1, 1] .001]
Y1 = 16*1 - 1.86*12 = 14.14 m when t1 = 1 sec.
Y2 = 16*1.001 - 1.86*1.0012 = 14.15227814 m when t2 = 1.001 sec.
So,
average Velocity = (14.15227814 - 14.14)/(1.001 - 1) (1.001 - 1)
12.28 m/s V avg = 12.27814 m/s (In two decimal places)
Part B.
Rock's immediate velocity will be determined by:
d[16t - 1.86t2]/dt = V= dy/dt
Velocity = 16*1 - 2*1.86*t
time = 1 second,
Velocity = 16 - 2*1.86*1
average velocity at time t is equal to V = 12.28 m/s.
For more such questions on velocity, Refer:
https://brainly.com/question/25749514
#SPJ4
y=6/7x+11/7 in standard form
Answers
Answer:
6x-
7y
=
-11
6x-7y=-11
What integer best represents
a withdrawal of $85?
Answers
Answer:
the answer is -85 good luck on your test or honework :)
Find the solution of
{Y≤-x² - 4x +3
Y>x^2+3

Answers
Thus, shaded region bounded between the interval (-2,7) and (0,3) are the solution of the given linear inequalities.
Explain about the graphical method?The 2 linear programming is optimised using the graphical approach. Finding the ideal answer is best done using a graphical approach when there are two choice factors in the problem. The collection of inequalities are bound by limitations in this method. The disparities are then shown using an XY plane graphic.
To represent the data visually, there are two different sorts of graphs. As follows: Time Series Graphs - Line Graph as an example. Frequency Polygon Graph is an illustration of a frequency distribution graph.For charting linear functions, there are three fundamental techniques. The first method involves tracing a line through a set of points that have been plotted. The second method makes use of the slope and y-intercept. The third method involves changing the identity function f(x)=x.Given linear inequalities are:
Y ≤ -x² - 4x +3
Y > x² + 3
Plot the graph of each equation using the graphing tool to get he solution.
From the graph:
Blue Region : Y ≤ -x² - 4x +3
green region: Y > x² + 3
Thus, shaded region bounded between the interval (-2,7) and (0,3) are the solution of the given linear inequalities.
know more about the graphical method
https://brainly.com/question/12115853
#SPJ1

Apply the distributive property to factor out the greatest common factor. 21e + 35 =
Answers
Answer:
7(3e+5) alternative form 92.08392
Step-by-step explanation:
Given PR = RQ, find the measure of arc RQ and the Measure of arc PQ.
12. mRQ=
13. mPQ=
The measure of LABD = 11x - 3 and mZACD = 8x + 15. Find the following:
112
14. x=
15. mLABD =
17
16. m AD =
3/11
110'
(11x-3) B
E
(8x + 15)*
Please show work

Answers
Answer:
x = 8
Step-by-step explanation:
Intersecting tangent and secant theorem:
If a tangent and a secant are drawn to the circle from a point from outside, the square of the measure of the tangent is equal to the product of the measures of the secant segment and its external secant segment.
x² = (4+12)*4
x² = 16 * 4
x² = 64
x = √64
x = 8
A tray contains 16 chocolate chip cookies and 12 oatmeal raisin cookies. HOw many ways can a child select 3 cookies that include at least 1 chocolate chip cookie
Answers
Answer:
Number of ways chosen cookies = 8 ways
Step-by-step explanation:
Given;
Total number of chocolate chip cookies = 16
Total number of oatmeal raisin cookies = 12
Total number of cookies choose = 3
At least 1 chocolate cookie
Find:
Number of ways chosen cookies
Computation;
Number of total ways = 2³
Number of total ways = 8
If at least on cookie is chocolate cookie,
Number of ways chosen cookies = Number of total ways - 1
Number of ways chosen cookies = 9 - 1
Number of ways chosen cookies = 8 ways
Using the tools you learned in this lesson, find all solutions (real and non-real) for the polynomial below. Explain how we can use Descartes' rule of signs to find the number of positive and negative real zeros of this polynomial. 3x^3-4x^2+11x+10=0To earn full credit please share all work, calculations and thinking. If you prefer you can do the work by hand on a piece of paper, take a picture of that work and upload it.
Answers
Step 1:
Write the polynomial equation
\(3x^3-4x^2+11x+10=0\)Step 2:
First, find the first factor of the polynomial.
The first factor is 3x + 2
\(\begin{gathered} \text{Divide }3x^3-4x^2+11x+10=0\text{ by 3x + 2 using long division} \\ \text{ x}^2\text{ - 2x + 5} \\ 3x\text{ + 2 }\sqrt[]{3x^3-4x^2+11x+10} \\ \text{ -(3x}^3+2x^2) \\ --------------------------- \\ \text{ -6x}^2+11x\text{ + 10} \\ \text{ -}(-6x^2\text{ - 4x)} \\ --------------------------- \\ \text{ 15x + 10} \\ \text{ -(15x + 10)} \\ ---------------------------------- \\ \text{ 0} \end{gathered}\)Step 3
The polynomial
\(3x^3-4x^2+11x+10canbeexpressionas(3x+2)((x^2-2x+5)\)Step 4:
\(\begin{gathered} \text{Use the quadratic formula to find the solution to } \\ x^2\text{ - 2x + 5} \\ x\text{ = }\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{a = 1, b = -2 and c = 5} \\ \text{x = }\frac{2\pm\sqrt[]{(-2)^2-4\times1\times5}}{2\times1} \\ \text{x = }\frac{2\pm\sqrt[]{4-20}}{2} \\ \text{x = }\frac{2\pm\sqrt[]{-16}}{2} \\ \text{x = }\frac{2\text{ + 4i}}{2}\text{ , x = }\frac{2\text{ - 4i}}{2} \\ \text{x = 1 + 2i , x = 1 - 2i} \end{gathered}\)Descartes rule of sign
It tells us that the number of positive real zeros in a polynomial function f(x) is the same or less than by an even number as the number of changes in the sign of the coefficients. The number of negative real zeros of the f(x) is the same as the number of changes in sign of the coefficients of the terms of f(-x) or less than this by an even number.
\(There\text{ are 1 negative real root x = }\frac{-2}{3}\)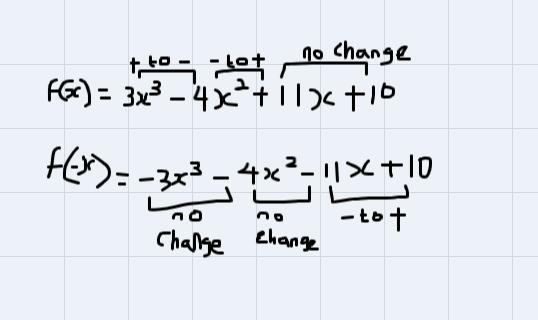
a. The cardinal number of {213, 214, 215, 216, ..., 912) is
Answers
Answer:
Step-by-step explanation:
a=213
l=912
let cardinal number=n
let c.d.=d
d=214-213=1
l=a+(n-1)d
912=213+(n-1)1
912=213+n-1
912-212=n
n=700
cardinal number=700
(a)
Using a calculator, or otherwise, determine the value of:
(i) 5.25 - 0.015
Answers
Answer:
5.235
Step-by-step explanation:
Just use a calculator
Else
5.250
-0.015
______
5.235
Add 0 to make it equal. Carry 1 from 5 of 5.2'5'0 to 0 and make it 10. 10g5 is 5. Then 4 remains .4-1 is 3. Others are normally subtracted.
Determine the whole number of standard deviations from the mean that include all
data values.
The mean price of the nonfiction books on a best-sellers list is $25.07; the standard
deviation is $2.62.
$26.95, $22.95, $24.00, $24.95, $29.95, $19.95, $24.95, $24.00, $27.95, $25.00
Answers
The number of standard deviations from the mean that include all
data values is two.
Standard Deviation could be a live that shows what proportion variation (such as unfold, dispersion, spread,) from the mean exists. the quality deviation indicates a “typical” deviation from the mean.it's a well-liked live of variability as a result of it returns to the initial units of live of the information setFrom the gathering of information, we will see that the minimum worth is $19.95 and also the most worth is $29.95. So , we would like to seek out the amount of normal deviations, let's decision it "a" , such that\(\overline x $\color \ - a\cdot\sigma \le 19.95}\) and \(\overline x $\color \ +a\cdot\sigma \geq 29.95}\)
Use the given values of mean \(\overline x\) and normal deviation (σ) to notice the worth of "a".
\(\overline x $\color \ - a\cdot\sigma \le 19.95}\\25.07\ - 2.62a \leq 19.95\\5.12\leq 2.62a\\1.9541\leq a\)
On rounding off we get a = 2
Checking another inequality
\(\overline x $\color \ + a\cdot\sigma \geq 29.95}\\25.07 \ + 2(2.62) \geq 29.95\\25.07 + 5.24 \geq 29.95\\30.31\geq 29.95\)
Thus , 2 standard deviation include the all values from the given set of data .
Learn more about standard deviation here :
https://brainly.com/question/12402189
#SPJ9
Need help asap please

Answers
The required value of x is 135° in the given polygon. which is the correct answer would be an option (A).
A polygon is given in the figure
According to the given question, the required solution would be as:
Number of sides = 8
The required value of x is the equal to measure of one Interior angle in the given polygon.
Interior angles of a polygon = (sides - 2) × 180°
In this case, the number of sides is 8
Sum of Interior angles = (8 - 2) × 180
Sum of Interior angles = (6) × 180
Sum of Interior angles = 1080°
the measure of one Interior angle = 180°/8
the measure of one Interior angle = 135°
Thus, the required value of x is 135°.
Learn more about the exterior angles here :
brainly.com/question/28835566
#SPJ1