Now let's look at the data from all the Buffalo. If we calculate the 60% confidence interval for every buffalo's count (i.e. data sample), how many Cls do we expect to contain the true mean? Store your answer in theoretical_hits. Then we need to check our theoretical answer with our actual data. Calculate the 60% confidence interval for each buffalo's count. Then commpute how many of those Cls contain the true mean. Assume that the true mean is 25,000. Store this value in sample_hits . Does this value match the theoretical value? It may be helpful to visualize the Confidence Intervals, along with the true mean. Create a plot for the Confidence intervals for the first 40 rows of the dataframe. Also plot true_mean=25000 as a horizontal dotted line. This plot will not be graded, but may help you get a better understanding of different confidence intervals for the same underlying population. We recommend looking into the ggplot package to help with this task.
Answers
15000 Cls should we expect to include the true mean if we compute the 60% confidence interval for each buffalo count (i.e., data sample).
Given that,
We have to calculate let's now examine the Buffalo's collective data. How many Cls should we expect to include the true mean if we compute the 60% confidence interval for each buffalo count (i.e., data sample).
We know that,
Theoretical hits= confidence interval × total no. of buffaloes
= 0.6×(buffaloes)
Sample hits = count among total no. of buffaloes, from which how many of inside 25000, that will be sample hits.
So,
=0.6×25000
=15000
Therefore, 15000 Cls should we expect to include the true mean if we compute the 60% confidence interval for each buffalo count (i.e., data sample).
To learn more about interval visit: https://brainly.com/question/2274635
#SPJ4
Related Questions
find the 9th term of the geometric sequence. 12,36,108,...
Answers
The 9th term of the given sequence is 78732.
The given sequence is 12, 36, 108... is a geometric sequence with a common ratio of 3.To find the 9th term of the given sequence, we will use the formula for the nth term of a geometric sequence, which is given by:
aₙ = a₁rⁿ⁻¹
Here, a₁ = 12 and r = 3.
Therefore, the formula for the nth term becomes:
aₙ = 12(3)ⁿ⁻¹
Now, we need to find the 9th term of the sequence. Hence, n = 9. Substituting the values of a₁ and r, and n in the formula, we get:
a₉ = 12(3)⁹⁻¹= 12(3)⁸= 12(6561)= 78732
For more question sequence
https://brainly.com/question/29017364?source=archive
#SPJ8
Work out 30% of $150
Answers
Answer:
$\(45\)
Step-by-step explanation:
\(30\)% \(\mathrm{of}\) $\(150\)
\(=\frac{30}{100}\times 150\\\)
\(=\) $\(45\)
Use the theoretical method to determine the probability of the following event.Sharing a birthday with another person when you both have birthdays in february (not born on a leap year)
Answers
Suppose There are 2 persons A and B, Both showing their birthdays in February 28 days The probability of A having a birthday in February = is 28 because There is a total of 28 possibilities.
Now, the Probability of B having a birthday in February same day as A = \(\frac{1}{28}\) on Because of only one Possibility.
Hence, Probability = \(\frac{28}{28} *\frac{1}{28} = \frac{1}{28}\).
A theoretical method can be proof that something is happening or a generalization of why. Indeed all statements specifying what is being measured or described all general statements about cause or domain theory are at least implicitly based. Theoretical research is the logical examination of systems of beliefs and assumptions. This type of research involves theorizing or defining the behavior of cybersystems and their environments and investigating or enforcing the implications of that definition.
Learn more about A theoretical method here:- https://brainly.com/question/1341226
#SPJ9
Cliff takes out a $5,000 personal loan with 7
fixed annual interest compounded monthly to pay for his wedding. He repays the loan in 2 year.s
How much total interest does Cliff pay on his loan?
Answers
Cliff pays a total interest of approximately $679.90 on his $5,000 loan.
To calculate the total interest paid on the loan, we need to use the formula for compound interest:
\(A = P(1 + r/n)^{(nt)}\)
Where:
A is the final amount (loan amount + interest)
P is the principal (loan amount)
r is the annual interest rate (in decimal form)
n is the number of times interest is compounded per year
t is the number of years
Given that Cliff takes out a $5,000 loan with a fixed annual interest rate of 7% compounded monthly, we can substitute the values into the formula:
P = $5,000
r = 7% = 0.07
n = 12 (monthly compounding)
t = 2 years
\(A = 5000(1 + 0.07/12)^{(12 \times 2)\)
Calculating this expression:
A ≈ 5000\((1.00583)^{(24)\)
A ≈ 5000(1.13598)
A ≈ 5679.90
The final amount (A) is the loan amount plus the total interest paid. Therefore, to find the total interest paid, we subtract the principal (P) from the final amount (A):
Total Interest = A - P
Total Interest = 5679.90 - 5000
Total Interest ≈ $679.90
For similar question on total interest.
https://brainly.com/question/29415701
#SPJ8
Need help asapppppppppdhhdhdhdhdhdhdhdhdhdhdhdhfh

Answers
Answer:
-11 to the power of 3
Step-by-step explanation:
The average duration of labor from the first contraction to the birth of the baby in women over 35 who have not previously given birth and who did not use any pharmaceuticals is 16 hours. Suppose you have a sample of 35 women who exercise daily, and who have an average duration of labor of 16.9 hours and a sample variance of 39.7 hours. You want to test the hypothesis that women who exercise daily have a different duration of labor than all women. Calculate the t statistic. To do this, you first need to calculate the estimated standard error. The estimated standard error is s M
Answers
Answer:
The estimated standard error is \(s_M = 1.065\).
The t statistic is \(t = 0.845\).
Step-by-step explanation:
The test statistic is:
\(t = \frac{X - \mu}{s_M}\)
In which X is the sample mean, \(\mu\) is the value tested at the null hypothesis, \(s_M = \frac{s}{\sqrt{n}}\) is the standard error, s is the standard deviation and n is the size of the sample.
The average duration of labor from the first contraction to the birth of the baby in women over 35 who have not previously given birth and who did not use any pharmaceuticals is 16 hours.
This means that \(\mu = 16\)
Suppose you have a sample of 35 women who exercise daily, and who have an average duration of labor of 16.9 hours and a sample variance of 39.7 hours.
This means that \(n = 35, X = 16.9, s = \sqrt{39.7} = 6.30\)
The estimated standard error is:
\(s_M = \frac{s}{\sqrt{n}} = \frac{6.30}{\sqrt{35}} = 1.065\)
The estimated standard error is \(s_M = 1.065\).
Calculate the t statistic.
\(t = \frac{X - \mu}{s_M}\)
\(t = \frac{16.9 - 16}{1.065}\)
\(t = 0.845\)
The t statistic is \(t = 0.845\)
Find the distance from the point N (3,5) to the graph of -2x + 3y + 3 = 0
Answers
Answer:
3.33
Step-by-step explanation:
1st get the line in point slope form (y = mx + b)
-2X + 3y + 3 = 0
3y = 2x - 3
y = (2/3)x - (3/3)
y = (2/3)x - 1 (slope = 2/3 and y-intercept is -1)
The distance from a point to a line is line segment starting at the point and perpendicular (shortest distance) to 1st line. A line perpendicular to the 1st line will have a negative inverse slope. So the line created in point slope form will look like
y = mx + b
y = (-3/2)x + b and using the given point (3,5)
5 = (-3/2)3 + b
5 - (-3/2)3 = b
5 + 9/2 = b
b = 19/2 So it's equation is
y = (-3/2)x + 19/2
At the point where the segment intersects the 1st line, that point must solve both equations, so we can set the equation equal to each other (both y's and both x's same).
(2/3)x -1 = (-3/2)x + 19/2
(2/3)x - (-3/2)x = 1 + 19/2
(2/3 + 3/2)x = 21/2
x = (21/2) / (2/3 + 3/2) = 4.846, now plug that into the 1st equation to get y
y = (2/3)x - 1
y = (2/3)4.846 - 1
y = 2.231 so the intersection point is (4.846,2.231) from (3,5).
Because of the pythagorean theorem (the two points form a right triangle) the distance will be
C**2 = A**2 + B**2
= (4.846 - 3)**2 + (2.231 - 5)**2
= 1.846**2 + (2.769)**2
C = 3.33
which of the following years were leap years according to the calendar used before the time of pope gregory: 1000, 1492, 1600, 1776?
Answers
The probability 1000, 1600, and 1776 were leap years according to the calendar used before the time of pope gregory, but 1492 was not.
The calendar used before the time of Pope Gregory was the Julian Calendar, which was introduced by Julius Caesar in 46 BC. This calendar used a system of leap years, where an extra day was added to the month of February every four years. This was to account for the fact that a solar year is slightly longer than 365 days. For a year to be a leap year under this system, it must be divisible by 4. Therefore, 1000, 1600, and 1776 were leap years according to the Julian Calendar, but 1492 was not since it is not divisible by 4. This calendar was replaced by the Gregorian Calendar in 1582, which uses a slightly modified leap year system. Under this system, a year is only a leap year if it is divisible by 4, but not if it is divisible by 100, unless it is also divisible by 400. Therefore, 1600 would still be a leap year under the Gregorian Calendar, but 1700, 1800, and 1900 would not be.
Learn more about probability here
https://brainly.com/question/30034780
#SPJ4
in this figure , m<1=(2x)° and m<2 = (6x-6)° what is m<1
Answers
Answer:
where is the figure?
Step-by-step explanation:
A
-pound bag of Kitty Kibbles is
. An
-pound bag of Feline Flavor is
. Which statement about the unit prices is true?
Feline Flavor has a higher unit price of
/pound.
Kitty Kibbles has a higher unit price of
/pound.
Kitty Kibbles has a higher unit price of
/pound.
Feline Flavor has a higher unit price of
/pound.
Answers
The statement about the unit prices which is true is Kitty Kibbles has a lower unit price of $1.30/pound.
The correct answer choice is option D.
How to solve unit prices?Cost of 16-pound bag of Kitty Kibbles = $20.80
Unit price of kitty kibbles = Price / number of pounds
= $20.80 / 16
= $1.30 per pound.
Cost of 8-pound bag of Feline flavor = $11.20
Unit price of feline flavor = Price / number of pounds
= $11.20 / 8
= $1.40 per pound
Ultimately, the unit price of kitty kibbles and feline flavor is $1.30 and $1.40 respectively.
Complete question:
A 16-pound bag of Kitty Kibbles is $20.80. An 8-pound bag of Feline Flavor is $11.20. Which statement about the unit prices is true?
A. Feline Flavor has a lower unit price of $1.40/pound.
B. Feline Flavor has a lower unit price of $1.30/pound.
C. Kitty Kibbles has a lower unit price of $1.40/pound.
D. Kitty Kibbles has a lower unit price of $1.30/pound.
Read more on unit price:
https://brainly.com/question/945712
#SPJ1
The half-life of a radioactive isotope is the time it takes for a quantity of the isotope to be reduced to half its initial mass. Starting with grams of a radioactive isotope, how much will be left after 4 half-lives?
Answers
After 4 half-lives, only 1/16th (or 0.0625) of the initial amount of the radioactive isotope will remain.
The amount of a radioactive isotope remaining after a certain number of half-lives can be calculated using the formula:
Amount remaining = Initial amount × (1/2)^(number of half-lives)
In this case, we are given the initial amount as "grams" and we want to find out the amount remaining after 4 half-lives.
So, the equation becomes:
Amount remaining = Initial amount × (1/2)^4
Since each half-life reduces the quantity to half, (1/2)^4 represents the fraction of the initial amount that will remain after 4 half-lives.
Simplifying the equation:
Amount remaining = Initial amount × (1/16)
Therefore, after 4 half-lives, only 1/16th (or 0.0625) of the initial amount of the radioactive isotope will remain.
for such more question on radioactive isotope
https://brainly.com/question/20596678
#SPJ8
Kanica wants to earn at least $750 this week in commission. What is the minimum amount she needs to sell in order to earn $750 if she earns a 7.5% commission on everything she sells? Round your answer to the nearest dollar if necessary.
Answers
Answer:
Total earning Kanica wants to make is at least $750
The commission she gets is 7.5 % Therefore to find the sales she should make we use :
(Total earnings * 100% )/ Commission
= (100 * 750) / 7.5
=75000/7.5
= $ 10,000
The minimum amount she needs to sell in order to earn $750 if she earns a 7.5% commission on everything she sells is $10,000.
What is the percentage?It's the ratio of two integers stated as a fraction of a hundred parts. It is a metric for comparing two sets of data, and it is expressed as a percentage using the percent symbol.
It is given that:
Kanica wants to earn at least $750 this week in commission.
Let x be the minimum amount she needs to sell in order to earn $750 if she earns a 7.5% commission on everything she sells.
The value of x can be found as follows:
x = 750/(7.5%)
x = (750/7.5)x100
x = $10,000
Thus, the minimum amount she needs to sell in order to earn $750 if she earns a 7.5% commission on everything she sells is $10,000.
Learn more about the percentage here:
brainly.com/question/8011401
#SPJ5
If there are penguins in the aquarium is full of fish, then this is an octopus write
this in Symbolic form

Answers
The compound statement "If there are penguins and the aquarium is full of fish, then this is an octopus" can be written in symbolic form as: r ∧ q → o
How to explain the informationLet's assign variables to represent the statements:
q: The aquarium is full of fish.
r: There are penguins.
The compound statement "If there are penguins and the aquarium is full of fish, then this is an octopus" can be written in symbolic form as: r ∧ q → o
∧ represents the logical operator "and" which connects the statements r and q.
→ represents the logical operator "implies" or "if...then".
o represents the statement "this is an octopus".
Learn more about compound statement on
https://brainly.com/question/28794655
#SPJ1
(a) The displacement (in centimeters) of a particle s moving back and forth along a straight line is given by the equation
s = 2 sin(t) + 3 cos(t),
where t is measured in seconds. (Round your answers to two decimal places.)
[1, 2]
[1, 1.1]
[1, 1.01]
[1, 1.001]
(b) Estimate the instantaneous velocity of the particle when
t = 1.
Answers
The displacements are 2.84 cm, 2.77 cm, 2.83 cm and 2.83 cm respectively.
Instantaneous velocity of the particle at t =,1 is 0.72 cm/s.
How to calculate displacement and velocity?a. To find the displacement of the particle at various times t, we can simply plug the given value of t into the equation s = 2 sin(t) + 3 cos(t) and evaluate:
[1, 2]: s = 2 sin(1) + 3 cos(1) = 2.84 cm
[1, 1.1]: s = 2 sin(1.1) + 3 cos(1.1) = 2.77 cm
[1, 1.01]: s = 2 sin(1.01) + 3 cos(1.01) = 2.83 cm
[1, 1.001]: s = 2 sin(1.001) + 3 cos(1.001) = 2.83 cm
b. To find the instantaneous velocity of the particle when t = 1, we need to find the derivative of the equation for displacement with respect to time, which will give us the velocity. The derivative is given by:
v(t) = ds/dt = 2 cos(t) - 3 sin(t)
Plugging in t = 1 into this equation, we find:
v(1) = 2 cos(1) - 3 sin(1) = 0.72 cm/s
So, the instantaneous velocity of the particle at t = 1 is approximately 0.72 cm/s.
Learn more on displacement here: https://brainly.com/question/12923892
#SPJ1
Find the volume of the tetrahedron with the given vertices. (4, 0, 0), (0, 4, 0), (0, 0, 1), (4, 4, 1)
Answers
Answer:
\(\mathbf{V = \dfrac{16}{3}}\)
Step-by-step explanation:
From the information given:
A = (4,0,0) B = (0,4,0) C = (0,0,1) D = (4,4,1)
\(\overline{ AB}\) = (0,4,0) - (4,0,0) = (-4, 4, 0)
\(\overline{ BC} =\) (0,0,1) - (0,4,0) = (0, -4, 1)
\(\overline{ CD}\) = (4,4,1) - (0,0,1) = (4, 4, 0)
The Volume of the tetrahedron \(V = \dfrac{1}{6} \bigg| AB \times BC \times CD \bigg|\)
The Volume of the tetrahedron \(V = \dfrac{1}{6} \left\begin{vmatrix}-4,&4&0\\0,&-4&1\\4&4&0\end{vmatrix}\right\)
\(V = \dfrac{1}{6}\bigg [ -4(-4 *0 - 1*4) -4(0*0-1*4) +0(0*4--4*4) \bigg ]\)
\(V = \dfrac{1}{6}\bigg [ -4(0 - 4) -4(0-4) +0(0+16) \bigg ]\)
\(V = \dfrac{1}{6}\bigg [ 16 + 16 +0 \bigg ]\)
\(V = \dfrac{1}{6}\bigg [ 32 \bigg ]\)
\(\mathbf{V = \dfrac{16}{3}}\)
Complete the fractions to make a true inequality, and explain your reasoning.
CLEAR CHECK
3
×
<
3
7
I know this because the fraction I made is
1
.
3
×
>
3
7
I know this because the fraction I made is
1
.
Answers
Complete the fractions to make a true inequality, and explain your reasoning.
CLEAR CHECK
3
×
<
3
7
Step-by-step explanation:
Write a second inequality with the same meaning -12<= a
Answers
Answer:
a\(\geq\)-12 or -48\(\leq\)4a
Step-by-step explanation:
Madison made the following table to record the height of each person in her family. Round her mom's height to the nearest half or whole.
dad- 6 3/8
mom- 5 5/8
madison- 5 1/6
jade- 4 5/6
ben- 3 1/2
Answers
Answer:
her height would be 6
Step-by-step explanation:
Since 5/8 is greater than 1/2 you have to look for the greatest closes number which would be one. So you just add that one to the 5 and you get 6.
Answer:
5 1/2
i promise loll
answer the questions below to find the total surface area of the can

Answers
The total surface area of the tomato ketchup given in the diagram can be determined as follows:
The total surface area of a shape is the addition of the areas of its individual surface.
So that the questions can be answered as thus:
A. To find the area of the given circle;
i. Area of a circle = \(\pi r^{2}\)
where r is the radius of the circle.
area of the circle = π\((2.5)^{2}\)
= 6.25\(\pi\)
ii. There are two identical circles in the cylinder.
iii. The total area of all circles = 2(6.25\(\pi\))
= 12.5\(\pi\) square inches
B. To find the area of the rectangle;
i. one side of the rectangle is 5 inches.
ii. The other side of the rectangle = 2\(\pi\)r
= 2(2.5)\(\pi\)
= 5\(\pi\) inches
iii. The area of the rectangle = l x b
= 5\(\pi\) x 5
= 25\(\pi\) square inches
C. Total surfce area of the cylinder = 5\(\pi\) + 25\(\pi\)
= 30\(\pi\) square inches
For more clarifications on total surface area of a cylinder, check: https://brainly.com/question/16990329
#SPJ1
Answer:
Step-by-step explanation:
First box
6.25
2
12.5
------
Second box
------
5
5
25
------
Last box
------
37.5
A shipping box is 36 inches by 24 inches by 18 inches
how many cubic feet can it hold
Answers
Answer:
To find the volume of the shipping box in cubic feet, we need to convert the dimensions from inches to feet and then calculate the volume.
Given:
Length = 36 inches
Width = 24 inches
Height = 18 inches
Converting the dimensions to feet:
Length = 36 inches / 12 inches/foot = 3 feet
Width = 24 inches / 12 inches/foot = 2 feet
Height = 18 inches / 12 inches/foot = 1.5 feet
Now, we can calculate the volume of the box by multiplying the length, width, and height:
Volume = Length * Width * Height
Volume = 3 feet * 2 feet * 1.5 feet
Volume = 9 cubic feet
Therefore, the shipping box can hold 9 cubic feet.
Step-by-step explanation:
First convert the units because it's asking for the cubic feet but they give us the measurements in inches.
To convert inches to feet we divide the number by 12.
36 ÷ 12 = 3
24 ÷ 12 = 2
18 ÷ 12 = 1.5
Now to find the volume, we multiply it all together.
3 × 2 × 1.5 = 9
It can hold 9 cubic feet.
Hope this helped!
Choose the correct statement. Consider the expression: 6.43
А
The product of one rational number and one irrational number is rational.
B
The product of one rational and one irrational number is irrational.
C
The product of two irrational numbers is irrational.
D
The product of two rational numbers is rational.
Answers
Answer:
D
Step-by-step explanation:
Goky kwiwiwjwjjwiwjwiw
Choose all of the statements that correctly compare the two functions shown.
Alec's rate of savings is greater than Beth's.
entific
Alec and Beth are saving at the same rate.
Alec started with more money than Beth
mulas
Time
maining
:19:23
Beth started with more money than Alec,
de les
At 10 days, Alec will have $1 more than Beth in savings,
Answers
Answer:
b, c and e
Step-by-step explanation:
Given
See attachment for functions
Required
Select all statements that contain both functions
First, calculate the rate (slope) of both functions.
This is calculated as:
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
For Alec's
\((x_1,y_1) = (0,3)\)
\((x_2,y_2) = (2,9)\)
So, the slope is:
\(m = \frac{9 - 3}{2 - 0}\)
\(m = \frac{6}{2}\)
\(m =3\)
For Beth's
\((x_1,y_1) = (5,17)\)
\((x_2,y_2) = (12,38)\)
So, the slope is:
\(m = \frac{38 - 17}{12 - 5}\)
\(m = \frac{21}{7}\)
\(m =3\)
Beth and Rec have the same slope. Hence, they save at the same rate.
Next, determine the amount they started with.
This implies that we calculate y when x = 0
From Alec's graph.
\((x,y) = (0,3)\)
Alec's initial savings is 3
For Beth's savings, we make use of slope formula.
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
\((x_1,y_1) = (5,17)\)
\((x_2,y_2) = (0,y)\)
So, we have:
\(3 =\frac{y - 17}{0 - 5}\)
\(3 =\frac{y - 17}{ - 5}\)
\(y - 17 = -15\)
\(y = 17 -15\)
\(y = 2\)
Beth's initial savings is 2
Hence, Alec started with more money
Next, is to determine who has more money after 10 days.
Since they save at the same rate, the difference in their savings after any number of days will be the difference in their initial savings.
The difference (d) is calculated as:
\(d = 3 - 2\)
\(d = 1\)
Hence, Alec will have $1 more than Beth after 10 days

Answer:
its bc and e or Alec and Beth are saving at the same rate. Alec started with more money than Beth. and At 10 days, Alec will have $1 more than Beth in savings.
Step-by-step explanation:
A large passenger airplane is making the 9,537-mile trip from New York to Singapore. During this flight, the plane will use 47,685 gallons of fuel, or 5 gallons per mile of flight. The function F(d) represents the amount of fuel, in gallons, consumed by the airplane on this trip after d miles of flight.
What is the domain of F(d)?
Answers
The domain of F(d) is: {d ∈ R | d ≥ 0}
What is Domain:The domain is a mathematical concept that refers to the set of all possible input values (independent variables) for which a function is defined. In other words, the domain of a function is the range of values that can be used as input to the function.
Here we have
A large passenger airplane is making the 9,537-mile trip from New York to Singapore. During this flight, the plane will use 47,685 gallons of fuel or 5 gallons per mile of flight.
The function F(d) represents the amount of fuel, in gallons, consumed by the airplane on this trip after d miles of flight.
Therefore, we can express F(d) as:
F(d) = 5d
The domain of F(d) represents the set of all valid values of d for which the function is defined.
In this case, d represents the distance flown by airplane, and it must be a non-negative number since the plane cannot fly a negative distance.
Therefore,
The domain of F(d) is: {d ∈ R | d ≥ 0}
Learn more about Domain at
https://brainly.com/question/29804413
#SPJ1
What is the equation of the line that passes through the point (6,1) and is parallel to the line x+3y=15
Answers
9514 1404 393
Answer:
x + 3y = 9
Step-by-step explanation:
The parallel line will have the same x- and y-coefficients. The new constant can be found by using the (x, y) values of the given point.
x + 3y = (6 +3(1)) = 9
The equation of the parallel line is ...
x + 3y = 9
y=3(2-1)2+1
Solución
Answers
Answer:
y = 7
Step-by-step explanation:
y = 3(2-1) 2 + 1
y = 3(1)(2) + 1
y = 6 + 1
y = 7
SOLVING THE SYSTEM BY ELIMINATION!

Answers
10x + 2y = 18
Then if we are subtracting the bottom equation from the pink box
10x + 2y = 18
-(10x -7y = -18)
9y = 36
y = 4
Evaluate the integral by making the given substitution. (Use C for the constant of integration.) x3(3 + x4)6 dx, u = 3 + x4 Evaluate the integral by making the given substitution. (Use C for the constant of integration.)
dt(1 â 3t)6, where u = 1 â 3t
Answers
The answer to this integration is - \(\frac{u^{7} }{28} + c\) .
u = 3 + x⁴
differentiate both sides,
⇒ du = 0 + 4x³ dx
⇒ du = 4x³ dx
⇒\(dx = \frac{du}{4x^{3} }\) ..........(1)
The integration is :
\(\int x^{3} ( 3 +x^{4} )^{6} dx\)
Substitute the values from equation (1)
= \(\int x^{3} u^{6} \frac{du}{4x^{3} }\)
= \(\frac{1}{4} \int u^{6} du\)
=\(\frac{1}{4} . \frac{u^{7} }{7} + c\) ( c = integration constant )
= \(\frac{u^{7} }{28} + c\)
Hence, the answer to this integration is - \(\frac{u^{7} }{28} + c\) .
Read more about integration :
https://brainly.com/question/27419605
#SPJ4
Help please.....its due today

Answers
“I hope this help us need anything just come back to me”
Find the range of the graphed function.A. -9 < y < 5B. y is all real numbers.C. O < y < 10D. y > 0
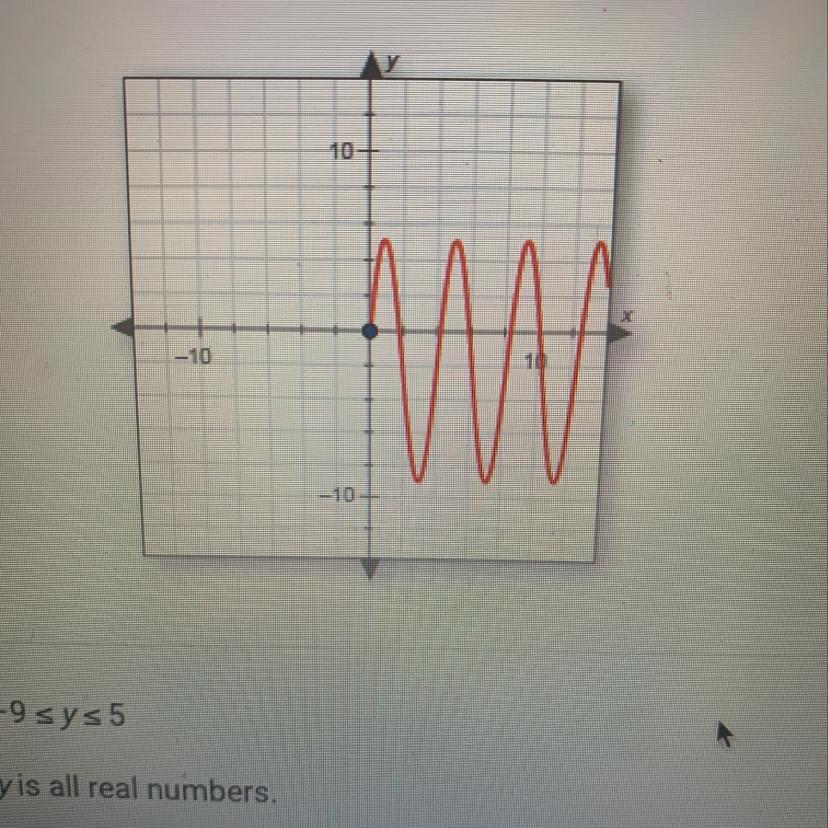
Answers
The range of a function is all the values that the function can take on the y-axis.
So, the y values of this function are between -9 and 5.
It means that the range is:
A. -9 < y < 5
What is the distance between point A(-2,-1) and point B (3,2)?

Answers
Answer:
5
Step-by-step explanation:
sorry if wrong