Need help! I HAVE 30 MIN! will pay for all work shown (ZELLE ONLY) Do all 3 please!

Answers
Answer: i gotchu
Step-by-step explanation:
1) Since the base of this function is greater than 1, this means its increasing exponentially (increases from left to right). So as x approaches positive infinity, y approaches positive infinity as well.
Domain (-∞,∞) Range (0,∞)
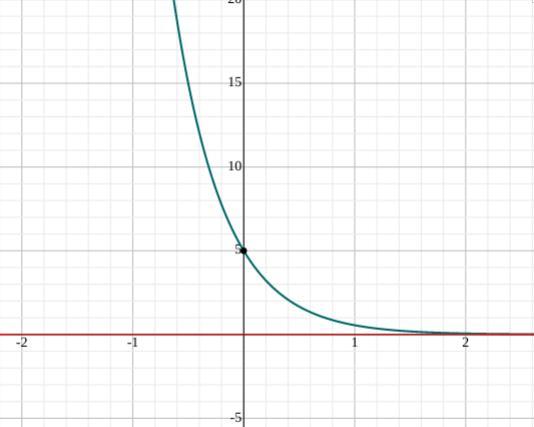
2) If the base changes to 1/9 the function would decrease. So as x approaches positive infinity, y approaches 0 (Check attached screenshot)
3) The "+5" raises the horizontal asymptote up 5 units. So the new equation for the horizontal asymptote is y=5.
The "x-2" shifts the x values to the right by 2 units.
u dont have to pay me, i literally just learned this like a month ago :)
Related Questions
length of a rectangle is 2 metre and the breadth is 50 find the ratio of a length to the breadth of a rectangle
Answers
explaining
not sure sorry good luck
A ship is anchored off a long straight shoreline that runs north and south. From two observation points
miles apart on shore, the bearings of the ship are
and
. What is the distance from the ship to each of the observation points? Round each answer to the nearest tenth of a mile.
The distance from the north most ship to the observation is
miles.
The distance from the south most ship to the observation is
miles.
Answers
The distance from the north most ship to the observation is 2.9 miles and the distance from the south most ship to the observation is 9.9 miles.
The bearing is defined as the angle measured clockwise from the north direction. A ship is anchored off a long straight shoreline that runs north and south.
From two observation points miles apart on shore, the bearings of the ship are 52 degrees and 134 degrees respectively. To find the distance from the ship to each of the observation points, we can use trigonometry.
Let's call the distance from the north observation point to the ship x, and the distance from the south observation point to the ship y. The bearings from the north and south observation points can be drawn as follows:
[asy]
unitsize(1cm);
pair O = (0,0), N = (-2,0), S = (2,0), A = (-2,1), B = (2,-1);
draw(O--N--A,Arrow);
draw(O--S--B,Arrow);
\(label("$52^\circ$", N + 0.3*dir(52), NE);\)
\(label("$134^\circ$", S + 0.3*dir(134), SE);\)
draw(O--A--B--cycle,dashed);
\(label("$x$", (N+A)/2, W);\)
\(label("$y$", (S+B)/2, E);\)
[/asy]
We can use the tangent function to find x and y, since we have the angle and opposite side.
From the north observation point, we have:
\($$\tan(52^\circ) = \frac{x}{2}$$$$x = 2\tan(52^\circ) \approx 2.95$$\)
From the south observation point, we have:
\($$\tan(134^\circ) = \frac{y}{2}$$$$y = 2\tan(134^\circ) \approx 9.88$$\)
Therefore, the distance from the north most ship to the observation is 2.9 miles and the distance from the south most ship to the observation is 9.9 miles.
Know more about trigonometry here:
https://brainly.com/question/13729598
#SPJ8
Exercise 3.62. A little boy plays outside in the yard. On his own he would come back inside at a random time uniformly distributed on the interval [0, 1]. (Let us take the units to be hours.) However, if the boy is not back inside in 45 minutes his mother brings him in. Let X be the time when the boy comes back inside (a) Find the cumulative distribution function F of X (b) Find the mean E(X) (c) Find the variance Var(X) Hint. You should see something analogous in Examples 3.20 and 3.38.
Answers
a) The cumulative distribution function F of X is: F(x) = P(X ≤ x) = 1
b) The mean E(X) is: E(X) = 0.5 hours.
c) The variance Var(X) is: the variance of X is approximately 0.0833 hours².
To find the cumulative distribution function (CDF) of X, we need to consider two cases: when the boy comes back inside before 45 minutes and when the boy is brought inside by his mother after 45 minutes.
(a) Cumulative Distribution Function (CDF) F of X:
For 0 ≤ x < 0.75 (when the boy comes back inside before 45 minutes):
Since the boy comes back inside uniformly distributed on the interval [0, 1], the CDF is simply the probability that the boy comes back inside before time x.
The probability of the boy coming back inside before x is equal to x, as it is a uniform distribution.
F(x) = P(X ≤ x) = x
For 0.75 ≤ x ≤ 1 (when the mother brings the boy inside after 45 minutes):
If the boy is not back inside at 45 minutes (0.75 hours), his mother brings him inside.
Therefore, the probability of the boy coming back inside before x in this case is 1.
F(x) = P(X ≤ x) = 1
(b) Mean (Expected Value) E(X):
The expected value of X, denoted by E(X), is the average time the boy spends outside before coming back inside.
For a uniform distribution on the interval [0, 1], the expected value is the midpoint of the interval.
Therefore, E(X) = (1 + 0) / 2 = 0.5 hours.
(c) Variance Var(X):
The variance of X, denoted by Var(X), measures the spread or variability of the random variable X around its mean.
For a uniform distribution on the interval [0, 1], the variance is given by:
Var(X) = (1² - 0²) / 12 = 1 / 12 ≈ 0.0833 hours²
So, the variance of X is approximately 0.0833 hours².
To learn more on probability click:
brainly.com/question/11234923
#SPJ4
11+11=4, 22+22=16, 33+33?
Answers
Sequence= 4, 16
Difference=12
16+12=28
Answer is...
33+33=28
These shapes are similar.
Find X.
5
X
5
30
24
30
Answers
The value of x is 4.
To determine the value of x, we can use the concept of similarity between shapes.
Similar shapes have corresponding sides that are proportional to each other.
Given the dimensions of the first shape as 5, x, and 5, and the dimensions of the second shape as 30, 24, and 30, we can set up the following proportion:
5/x = 30/24
To solve for x, we can cross-multiply:
30 · x = 5 · 24
30x = 120
Dividing both sides of the equation by 30:
x = 120 / 30
x = 4
Therefore, the value of x is 4.
Learn more about concept of similarity click;
https://brainly.com/question/32217666
#SPJ1
643 N
5
2
T
-5-4-3-2-1₁-
-2
-3
-4
-5
y
-
2 3 4 5
X
What is the range of the function on the graph?
O all real numbers
Oall real numbers greater than or equal to 0
all real numbers greater than or equal to 1
all real numbers greater than or equal to 2

Answers
The range of the function is all real numbers.
What is Function?In mathematics, a function is an expression, rule, or law that specifies a relationship between two variables (the independent variable and the dependent variable). Functions are common in mathematics and are required for the formulation of physical relationships in the sciences.
We know,
The x-values (Input values) on the graph define the domain of the function.
and, The y-values (output values) on the graph determine the range of a function.
From the graph attached,
Here the x value start from +1 to ∞.
Thus, the range of the function is all real numbers.
Learn more about Function here:
https://brainly.com/question/17347670
#SPJ5
Pls help I need this answer now As part of a class project, a university student surveyed the students in the cafeteria lunch line to look for a relationship between eye color and hair color among students. The table below contains the results of the survey.

Answers
Rounding the answer to two decimal places, the relative frequency of students with red hair among the sample population of students with gray eyes is approximately 0.63. Option D
To find the relative frequency of students with red hair among the sample population of students with gray eyes, we need to divide the number of students with gray eyes and red hair by the total number of students with gray eyes.
From the given table, we can see that there are 22 students with gray eyes and red hair.
The total number of students with gray eyes is the marginal total for gray eyes, which is 35.
To find the relative frequency, we divide the number of students with gray eyes and red hair by the total number of students with gray eyes:
Relative frequency = Number of students with gray eyes and red hair / Total number of students with gray eyes
Relative frequency = 22 / 35
Simplifying the fraction, we have:
Relative frequency = 0.6286
Rounding the answer to two decimal places, the relative frequency of students with red hair among the sample population of students with gray eyes is approximately 0.63.
Therefore, the correct answer is option OD) 0.63.
For more such questions on relative frequency visit:
https://brainly.com/question/3857836
#SPJ8
what is the solution to the inequality 8(7-x)<64
Answers
Answer: x>-1
Step-by-step explanation:
Isolate the variable by dividing each side by factors that don't contain the variable.
Aliyah $24 to spend on seven pencils. After buying them she had $10.how much did each Pencil cost?
Answers
Answer:
2 dollars
Step-by-step explanation:
24-10=14
7 pencils cost 14 dollars
1 pencil costs 2 dollars
please give me brainliest!!
Divide by 7 = 2
1 Pencil = $2
S. Jamie was really struggling to multiply two digit numbers together. Mrs. Brack helped her with the
problem 13.(20•5) by multiplying 20 by 5 and then by 13, which is 1300. What property did Mrs. Brack
use?
Answers
The property applied is the associative property
Algebraic propertiesThere are several algebraic properties in mathematics; each of which have their own applications
Some of these properties are:
CommutativeDistributiveAssociativeIdentityThe mathematical expression is given as:
\(13 \cdot (20 \cdot 5)\)
And it is calculated as follows:
\(13 \cdot (20 \cdot 5) = 13 \cdot 100\)
\(13 \cdot (20 \cdot 5) = 13 00\)
The property applied above is the associative property
Read more about mathematical properties at:
https://brainly.com/question/10628093
Find the magnitude and direction (in degrees) of the vector. (Assume 0° ≤ < 360°.)
= 6i + 2sqrt3j
Answers
\(6i~~ + ~~2\sqrt{3}j\implies < \stackrel{a}{6}~~,~~\stackrel{b}{2\sqrt{3}} > \\\\[-0.35em] ~\dotfill\\\\ \stackrel{magnitude}{\sqrt{a^2+b^2}}\implies \sqrt{6^2+(2\sqrt{3})^2}\implies \sqrt{36+(2^2\cdot 3)}\implies \sqrt{36+12}\implies \sqrt{48} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{direction}{tan^{-1}\left( \cfrac{b}{a}\right)}\implies tan^{-1}\left( \cfrac{2\sqrt{3}}{6} \right)\implies tan^{-1}\left( \cfrac{\sqrt{3}}{3} \right) \\\\\\ tan^{-1}\left( \cfrac{1}{\sqrt{3}} \right)\implies 30^o\)
valuate −8 + 10 × 4 ÷ (−2). Question 25 options: −4 −28 −3 −20
Answers
Answer: its -28
Step-by-step explanation:
i dont know i used a app
Helpi really need this

Answers
Answer:
The height of the flagpole is about 25.6 feet.
Step-by-step explanation:
The figure is omitted--please sketch it.
Put your calculator in degree mode.
Let h be the height of the flagpole.
\( \tan(52) = \frac{h}{20} \)
\(h = 20 \tan(52) = 25.6\)
A plane flying with a constant speed of 360 km/h passes over a ground radar station at an altitude of 1 km and climbs at an angle of 30°. At what rate (in km/h) is the distance from the plane to the radar station increasing a minute later? (Round your answer to the nearest whole number.)
Answers
The rate (in km/h) at which the distance from the plane to the radar station is increasing a minute later is 0 km/h (rounded to the nearest whole number).
To solve this problem, we can use the concepts of trigonometry and related rates.
Let's denote the distance from the plane to the radar station as D(t), where t represents time. We want to find the rate at which D is changing with respect to time (dD/dt) one minute later.
Given:
The plane is flying with a constant speed of 360 km/h.
The plane passes over the radar station at an altitude of 1 km.
The plane is climbing at an angle of 30°.
We can visualize the situation as a right triangle, with the ground radar station at one vertex, the plane at another vertex, and the distance between them (D) as the hypotenuse. The altitude of the plane forms a vertical side, and the horizontal distance between the plane and the radar station forms the other side.
We can use the trigonometric relationship of sine to relate the altitude, angle, and hypotenuse:
sin(30°) = 1/D.
To find dD/dt, we can differentiate both sides of this equation with respect to time:
cos(30°) * d(30°)/dt = -1/D^2 * dD/dt.
Since the plane is flying with a constant speed, the rate of change of the angle (d(30°)/dt) is zero. Thus, the equation simplifies to:
cos(30°) * 0 = -1/D^2 * dD/dt.
We can substitute the known values:
cos(30°) = √3/2,
D = 1 km.
Therefore, we have:
√3/2 * 0 = -1/(1^2) * dD/dt.
Simplifying further:
0 = -1 * dD/dt.
This implies that the rate at which the distance from the plane to the radar station is changing is zero. In other words, the distance remains constant.
for such more question on distance
https://brainly.com/question/7243416
#SPJ8
the sum of two numbers is 22, and their difference is 12. set up two equations to solve using elimination to help you find the numbers. enter the lesser of the two numbers here:
Answers
When the sum of two numbers is 22, and their difference is 12, the lesser of the two numbers is 5.
What is equation?An equation is a formula in mathematics that expresses the equality of two expressions by connecting them with the equals sign =. In its most basic form, an equation is a mathematical statement that shows that two mathematical expressions are equal. 3x + 5 = 14, for example, is an equation in which 3x + 5 and 14 are two expressions separated by a 'equal' sign. A mathematical equation that depicts the relationship between two expressions on opposite sides of the sign. It mostly consists of one variable and one equal to symbol. 2x - 4 = 2 is an example.
Here,
Let numbers be a and b.
a+b=22
a=22-b
b-a=12
b-(22-b)=12
2b-22=12
2b=34
b=17
a=5
The lesser of the two numbers is 5 when the sum of two numbers is 22, and their difference is 12.
To know more about equation,
https://brainly.com/question/2228446
#SPJ4
common differences of the following Aps 12,14,16,18,20.....
Answers
Answer:
2
Step-by-step explanation:
The common difference is the difference between two consecutive terms in an arithmetic progression
Consider the following triangle.
a = 6.0, b = 7.7, c = 13.6
Determine whether the Law of Sines or the Law of Cosines is needed to solve the triangle.
O Law of Sines
O Law of Cosines
Solve (if possible) the triangle. If two solutions exist, find both. Round your answers to two decimal pl
A =
B =
C =
Need Help?
0
O
O
Read It

Answers
To determine whether the Law of Sines or the Law of Cosines is needed to solve the triangle, we can compare the given information with the formulas for each law.
The Law of Sines states:
a / sin(A) = b / sin(B) = c / sin(C)
The Law of Cosines states:
c^2 = a^2 + b^2 - 2ab * cos(C)
In this case, we are given the lengths of all three sides of the triangle (a = 6.0, b = 7.7, c = 13.6). Therefore, we have enough information to use the Law of Cosines to solve the triangle.
Using the Law of Cosines, we can find the measures of the angles:
c^2 = a^2 + b^2 - 2ab * cos(C)
(13.6)^2 = (6.0)^2 + (7.7)^2 - 2 * 6.0 * 7.7 * cos(C)
184.96 = 36 + 59.29 - 92.4 * cos(C)
184.96 = 95.29 - 92.4 * cos(C)
92.67 = -92.4 * cos(C)
cos(C) ≈ -1
Since the cosine of an angle cannot be greater than 1 or less than -1, it is not possible for the given triangle to have an angle with a cosine of -1. Therefore, the triangle is not solvable with the given side lengths.
In this case, the Law of Cosines is needed, but the triangle cannot be solved with the given information.
What the meaning of "a sequence of length n"?

Answers
In mathematics, a sequence is an ordered list of elements, often denoted by brackets or parentheses.
What the meaning of "a sequence of length n"?The term "a sequence of length n" refers to a sequence that contains a specific number of elements, where the number of elements is denoted by "n."
When the domain of a function is the set of natural numbers (N), it is called an infinite sequence. An infinite sequence can be thought of as an ordered list that continues indefinitely.
Read more on sequences here https://brainly.com/question/6561461
#SPJ1
To find the distance between (-2,-3) and (4,1), Peggy's teacher drew a diagram and marked blue lines to represent the legs of a right triangle. Peggy then used 42 and 62 to find the distance represented by the red segment. What distance did she find ?
A √114
B √52
C 2020
D 5252
E 25

Answers
By using the formula for the distance we will see that the correct option is B:
√52
What distance did she find?
We will use the general formula to find the distance between two points (a, b) and (c, d)
it is:
distance = √( (a - c)^2 + (b - d)^2)
Here we want to find the distance between the points (-2,-3) and (4,1), if we use the above formula we will get:
distance = √( (-2 - 4)^2 + (-3 - 1)^2) = √( 36 + 16)
distance = √52
The correct option is B.
Learn more about the distance between two points:
https://brainly.com/question/7243416
#SPJ1
Seraphina says that ΔKLM is a right triangle. Is she correct?
Seraphina is correct. The sum of the squares of the two legs of the triangle is equal to the square of the hypotenuse.
Seraphina is not correct. The sum of the squares of the two legs of the triangle is not equal to the square of the hypotenuse.
Seraphina is correct. In the diagram, side KM looks perpendicular to side ML, so the triangle must be a right triangle.
Seraphina is not correct. The sum of the legs, 12 cm and 16 cm, does not equal the length of the hypotenuse, 19 cm.

Answers
Answer:
B. Seraphina is not correct. The sum of the squares of the two legs of the triangle is not equal to the square of the hypotenuse.
Step-by-step explanation:
If KLM is a right triangle, then 12^2+16^2=19^2,
144+256 = 361
400 = 361 false
so, KLM is not a right triangle as the sum of the squares of the two legs are not equal to the square of the hypotenuse.
The sum of the squares of the two legs of the triangle is not equal to the square of the hypotenuse. Seraphina is incorrect.
What is a Pythagoras Theorem?If ABC is a triangle with AC as the hypotenuse and angle B with 90 degrees then we have:
|AC|^2 = |AB|^2 + |BC|^2
where |AB| = length of line segment AB. (AB and BC are the rest of the two sides of that triangle ABC, AC being the hypotenuse).
Seraphina says that ΔKLM is a right triangle.
Let us check whether triangle ΔKLM is a right triangle or not.
By the Pythagoras theorem, we have
19² = 16² + 12²
361 = 256 + 144
361 ≠ 400
Thus, the triangle is not a right triangle.
Learn more about the Pythagoras theorem here:
https://brainly.com/question/12105522
#SPJ2
When comparing two box-plots that show the same type of information, what determines agreement within the data?
A.the range of the quartiles in each data set
B.the median of each data set
C.the mean of each data set
D.the number of values in each data set
Answers
Answer:
c.the mean of each data set
Answer:
A
Step-by-step explanation:
Solve each of the quadratic equations.
PT. 1
3x = 0.5x2
A. x = -6 or x = 0
B. x = -4 or x = 3
C. x = -2
D. x = 1.5 x = 0 or x = 6
PT.2
0 = 5x2 - 2x + 6
A. x= 1±3i/2
B. x=1±√11/5
C. x=1±I√29/5
Answers
Answer:
the answer to pt 1 is D. x=1.5 x=0 or x=6
and the answer to part 2 is C. x=1±I√29/5
Step-by-step explanation:
1. The solution of this equation is x = 0 or x = 6 which is option D.
2. The solution of this equation is \(x = \dfrac{1 \pm i\sqrt{29}}{5}\) which is option C.
Use the concept of quadratic equation defined as:
The definition of a quadratic as a second-degree polynomial equation demands that at least one squared term must be included. It also goes by the name quadratic equations.
The quadratic equation has the following generic form:
ax² + bx + c = 0
1. The given quadratic equation is,
3x = 0.5x²
Rearranging it,
0.5x² - 3x = 0
Common out x,
x(0.5x - 3) = o
Then we have,
x = 0 or,
0.5x - 3 = 0
Add 3 on both sides,
0.5x = 3
Divide both sides by 0.5,
x = 3/0.5
x = 6
Hence the solution of this quadratic equation is,
x = 0 and x = 6 which is option D.
2. The given quadratic equation is:
0 = 5x² - 2x + 6
It can be written as,
5x² - 2x + 6 = 0
Since we know the quadrature formula for ax² + bx + c = 0 is,
\(x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
Here we have,
a = 5
b = -2
c = 6
Substitute values into the formula,
\(x = \dfrac{2 \pm \sqrt{4 - 120}}{10}\\\\x = \dfrac{1 \pm i\sqrt{29}}{5} \text{ }\text{ \text{ }} \text{\text{ }\ since } \sqrt{-1} = i\)
Hence, option C is correct.
To learn more about quadratic equations visit:
https://brainly.com/question/30098550
#SPJ7
The complete question is:
Solve each of the quadratic equations.
PT. 1
3x = 0.5x²
A. x = -6 or x = 0
B. x = -4 or x = 3
C. x = -2 or x = 1.5
D. x = 0 or x = 6
PT.2
0 = 5x² - 2x + 6
A. \(x = \dfrac{1 \pm 3i}{5}\)
B. \(x = \dfrac{1 \pm i\sqrt{11}}{5}\)
C. \(x = \dfrac{1 \pm i\sqrt{29}}{5}\)
what is a equivalent expression for 4(x-2)
Answers
help with theses answer please

Answers
Answer: correct me if I’m wrong
Step-by-step explanation:

= Answer:
Find the y-intercept of 2x - y = -16
Answers
9 = ln(x + 5)
Solve this equation for x. Round your answer to the nearest hundredth.
Answers
Answer:
x ≈ 8098.08
Step-by-step explanation:
using the rule of logarithms
\(log_{b}\) x = n ⇒ x = \(b^{n}\)
note that ln represents \(log_{e}\)
given
9 = ln(x + 5) or
ln(x + 5) = 9 , or \(log_{e}\) (x + 5) = 9 , then
x + 5 = \(e^{9}\) ( subtract 5 from both sides )
x = \(e^{9}\) - 5 ≈ 8103.08 - 5 = 8098.08 ( to the nearest hundredth )
Please help!! (Solve for x)

Answers
The value of x using the theorem of intersecting secants is 10
How to calculate the value of xFrom the question, we have the following parameters that can be used in our computation:
intersecting secants
Using the intersecting secants equation, we have
8 * (8 + x) = 6 * (6 + 18)
Evaluate the like terms
So, we have
8 * (8 + x) = 6 * 24
Divide both sides by 8
8 + x = 6 * 3
So, we have
8 + x = 18
Subtract 8 from both sides
x = 10
Hence, the value of x is 10
Read more about intersecting secants at
https://brainly.com/question/26340897
#SPJ1
Complete the square to transform the expression x ^ 2 - 2x - 2 into the form a * (x - h) ^ 2 +
k.
(x - 1) ^ 2 + 3
(x - 1) ^ 2 - 3
(x - 2) ^ 2 - 3
O (x - 2) ^ 2 + 3
Answers
By completing the square, the vertex form of quadratic equation is (x - 1)² - 3.
How to complete the square in a quadratic equation
In this question we find a quadratic equation in standard form, which must be modified into vertex form by completing the square, which consists in modifying part of the equation into a perfect square trinomial. The vertex form of the quadratic equation is:
y = C · (x - h)² + k
First, write the polynomial in standard form:
x² - 2 · x - 2
Second, use algebra properties to expand the expression:
(x² - 2 · x - 2) + 0
(x² - 2 · x - 2) + 3 - 3
(x² - 2 · x + 1) - 3
Third, use the definition of perfect square trinomial:
(x - 1)² - 3
To learn more on quadratic equations: https://brainly.com/question/29269455
#SPJ1
Is the statement true or false? If it is true, give a convincing argument. If it is false, give a counterexample. A circle can always be circumscribed about a quadrilateral whose opposite angles are supplementary. Choose the correct answer below. ... O A. False, because opposite angles in an inscribed quadrilateral intercept overlapping arcs totaling 180°. OB. True, because the opposite angles form a linear pair. O C. True, because opposite angles in an inscribed quadrilateral intercept non-overlapping arcs totaling 360°. O D. False, because the opposite angles form a linear pair.
Answers
A quadrilateral is a polygon with four sides and four vertices. It is a closed two-dimensional shape that can be classified into different types based on the lengths of its sides and the measures of its angles. Some common types of quadrilaterals include squares, rectangles, etc.
Solution with the explanation:The statement is false, and a counterexample can be constructed. Consider a quadrilateral with opposite angles of 120° and 60°, such as an isosceles trapezoid with legs of length 1 and bases of length 2. The sum of the opposite angles is 180°, so they are supplementary. However, it can be shown that no circle can be circumscribed about this quadrilateral. Therefore, the correct answer is D: False, because the opposite angles form a linear pair.
To know more about angles
https://brainly.com/question/28451077
#SPJ9
Dylan had 300 5p coins in a box last month. He now has 360 5p coins. Find the percentage increase.
Answers
Therefore the percentage increase is 72
72