My time is running out does anyone know how to do this i will give brainlist !!!!!!!!!!!!!!!!!!
no trolling
Answers
Answer:
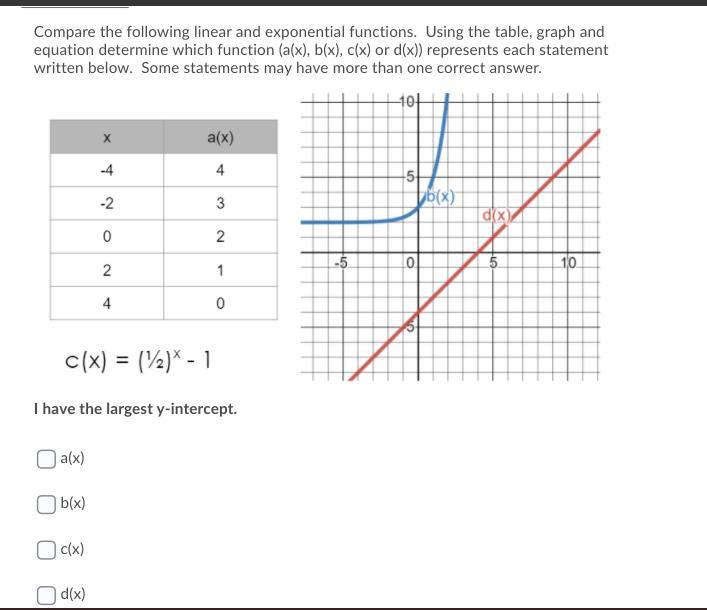
b(x)
Step-by-step explanation:
From the table for a(x)
The y- intercept where x = 0 is 2
For b(x) the curve crosses the y- axis at y = 3 ← y- intercept
c(x) = \((\frac{1}{2}) ^{x}\) - 1
To find the y- intercept let x = 0 , then
f(0) = \((\frac{1}{2}) ^{0}\) - 1 = 1 - 1 = 0 ← y- intercept
The graph of d(x) crosses the y- axis at (0, - 4 )
Then y- intercept = - 4
The largest y- intercept is 3 , that is b(x)
Related Questions
Multiply the starting price by the right term that uses the compound average to show that the arithmetic mean does not recover the final price while the geometric and continuous means do. Convert the percent averages to fractions.
$53. 07 x (1 + arith mean) 3 = 53.07 x (1 + #21 %) 3 = #22
$53. 07 x (1 + geom mean) 3 = 53.07 x (1 + #23 %) 3 = $ #24
$53. 07 x e cont mean x 3 = 53.07 x e #25 % x 3 = $ #26
I need help filling out numbers #21 through #26
Answers
The values for numbers #21 through #26 are as follows:
#21: 2.33% or 0.0233. #22: $56.4842. #23: 1.85% or 0.0185. #24: $56.4148. #25: 3.64% or 0.0364. #26: $57.4397
#21: 2.33% (arithmetic mean as a fraction: 0.0233)
#22: $56.4842 (result of the calculation)
#23: 1.85% (geometric mean as a fraction: 0.0185)
#24: $56.4148 (result of the calculation)
#25: 3.64% (continuous mean as a fraction: 0.0364)
#26: $57.4397 (result of the calculation)
To fill out numbers #21 through #26, we need to calculate the values for each term using the given information and convert the percentages to fractions.
#21: The arithmetic mean is given as a percentage. Convert it to a fraction by dividing by 100. Therefore, #21 = 2.33% = 0.0233.
#22: Multiply the starting price ($53.07) by the compound factor (1 + arithmetic mean)^3. Substitute the value of #21 into the calculation. Therefore, #22 = $53.07 x (1 + 0.0233)^3 = $56.4842.
#23: The geometric mean is given as a percentage. Convert it to a fraction by dividing by 100. Therefore, #23 = 1.85% = 0.0185.
#24: Multiply the starting price ($53.07) by the compound factor (1 + geometric mean)^3. Substitute the value of #23 into the calculation. Therefore, #24 = $53.07 x (1 + 0.0185)^3 = $56.4148.
#25: The continuous mean is given as a percentage. Convert it to a fraction by dividing by 100. Therefore, #25 = 3.64% = 0.0364.
#26: Multiply the starting price ($53.07) by the continuous factor e^(continuous mean x 3). Substitute the value of #25 into the calculation. Therefore, #26 = $53.07 x e^(0.0364 x 3) = $57.4397.
Hence, the values for numbers #21 through #26 are as calculated above.
To learn more about fraction, click here: brainly.com/question/28372533
#SPJ11
pls answer. and show your solution.

Answers
Answer:
23, - 46, 57, 10, 12
Step-by-step explanation:
(a)
2x + 5 = 2(9) + 5 = 18 + 5 = 23
(b)
4x - 2 = 4(- 11) - 2 = - 44 - 2 = - 46
(c)
x² + 21 = (- 6)² + 21 = 36 + 21 = 57
(d)
\(\sqrt{x}\) - 1 = \(\sqrt{121}\) - 1 = 11 - 1 = 10
(e)
\(\frac{x}{8}\) + \(\sqrt[3]{x}\) = \(\frac{64}{8}\) + \(\sqrt[3]{64}\) = 8 + 4 = 12
I need help with this

Answers
Using derivatives, it is found that regarding the tangent line to the function, we have that:
The slope is of 962.The equation of the line is y = 962x - 5119.What is a linear function?A linear function is modeled by:
y = mx + b
In which:
m is the slope, which is the rate of change, that is, by how much y changes when x changes by 1.b is the y-intercept, which is the value of y when x = 0, and can also be interpreted as the initial value of the function.The slope of the line tangent to a function f(x) at x = x' is given by f'(x'). In this problem, the function is given by:
f(x) = 5x³ + 2x + 1.
The derivative is given by:
f'(x) = 15x² + 2.
Hence the slope at x = 8 is:
m = f'(8) = 15(8)² + 2 = 962.
The line goes through the point (8,f(8)), hence:
f(8) = 5(8)³ + 2(8) + 1 = 2577.
Hence:
y = 962x + b
2577 = 962(8) + b
b = -5119.
Hence the equation is:
y = 962x - 5119.
More can be learned about tangent lines at https://brainly.com/question/8174665
#SPJ1
Plz help. Write the slope intercept form of the equation

Answers
Answer:
2nd option is correct
Step-by-step explanation:
x +2y=14
2y = -x + 14
y= -x/2 +7
Answer:
-1/2
Step-by-step explanation:
So I am not certain but there is a website for things these.

Alex earns a weekly base salary of $650 as a car salesman. He also earns a 9% commission on his monthly sales after the first $10,000. What was his total salary this month if he sold 7 cars whose average price was $4,500 each?
Answers
The total salary for the month will be $4535
How to calculate the value?From the information, Alex earns a weekly base salary of $650 as a car salesman. He also earns a 9% commission on his monthly sales after the first $10,000.
If he sold 7 cars whose average price was $4,500 each. The total amount will be:
= $4500 × 7.
= $31500
The commission will be
= 9% × ($31500 × $10000)
= 9% × $21500
= $1935
The total salary for the month will be:
= ($650 × 4) + $1935
= $4535
Learn more about commission on;
brainly.com/question/25169847
#SPJ1
GUYS I NEED HELP PLS

Answers
Answer:
y= 14.25x
k=14.25

If f is a differentiable function and g(x) = x f(x), use the definition of a derivate to show that g'(x) = x f'(x) + f(x).
Answers
The given statement "If f is a differentiable function and g(x) = x f(x), then g'(x) = x f'(x) + f(x)." is true and proved by using the definition of the derivative.
We can use the definition of the derivative to show that g'(x) = x f'(x) + f(x).
By the definition of the derivative, we have:
g'(x) = lim(h → 0) [g(x + h) - g(x)] / h
Substituting g(x) = x f(x), we get
g'(x) = lim(h → 0) [(x + h) f(x + h) - x f(x)] / h
Expanding the expression, we get
g'(x) = lim(h → 0) [x f(x + h) + h f(x + h) - x f(x)] / h
g'(x) = lim(h → 0) [x f(x + h) - x f(x)] / h + lim(h → 0) [h f(x + h)] / h
Using the definition of the derivative again, we can simplify the first term to get
g'(x) = x lim(h → 0) [f(x + h) - f(x)] / h + lim(h → 0) [h f(x + h)] / h
g'(x) = x f'(x) + lim(h → 0) [h f(x + h)] / h
Since f is differentiable, we know that f(x + h) - f(x) = h f'(x) + o(h), where o(h) represents a function that goes to zero faster than h as h approaches zero.
Substituting this expression into the second term, we get
g'(x) = x f'(x) + lim(h → 0) [h f(x + h)] / h
g'(x) = x f'(x) + f(x)
Therefore, we have shown that g'(x) = x f'(x) + f(x) using the definition of the derivative.
To know more about differentiable function:
https://brainly.com/question/30079101
#SPJ4
Please help me :((((

Answers
Answer:
Domain: {5, 9, 6, 3, 8}
Step-by-step explanation:
The set of first components (x-coordinates) in the ordered pairs is the domain of the relation. The domain is the set of values that serve as inputs into functions.
In the given relation, the domain is the set of x-coordinates of each ordered pair. The range is the set of y-coordinates.
Therefore, the domain of the relation is: {5, 9, 6, 3, 8}.
Please mark my answers as the Brainliest, if you find this helpful :)
what are a couple ways to simplify 3(x-5)-4=17
Answers
Simplifying
3(x + -5) + -4 = 17
Reorder the terms:
3(-5 + x) + -4 = 17
(-5 * 3 + x * 3) + -4 = 17
(-15 + 3x) + -4 = 17
Reorder the terms:
-15 + -4 + 3x = 17
Combine like terms: -15 + -4 = -19
-19 + 3x = 17
Solving
-19 + 3x = 17
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '19' to each side of the equation.
-19 + 19 + 3x = 17 + 19
Combine like terms: -19 + 19 = 0
0 + 3x = 17 + 19
3x = 17 + 19
Combine like terms: 17 + 19 = 36
3x = 36
Divide each side by '3'.
x = 12
Simplifying
x = 12
A section of a circle has both endpoints on the circle. What is the section of the circle called?arcradiuschorddiameter
Answers
Given
A section of a circle has both endpoints on the circle.
To find: What is the section of the circle.
Explanation:
It is given that,
A section of a circle has both endpoints on the circle.
Since A chord is a line segment with both end points on the circle.
Final result: Then, the section of the circle is called Chord.
Answer: chord
Step-by-step explanation:
Identify the axis of symmetry of the parabola. Kind of urgent lol

Answers
Answer: x = 4
Step-by-step explanation:
The axis of symmetry is the middle of the parabola that cuts it into two equal pieces.
Here it is fairly easy to spot, and the middle, or axis of symmetry, is x = 4.
Which of the following criteria are used when deciding upon the
inclusion of a variable? Check all that apply.
Group of answer choices
A-Theory
B-t-statistic
C-Bias
D-Adjusted R^2
Answers
the criteria used when deciding upon the inclusion of a variable are A - Theory, B - t-statistic, C - Bias, and D - Adjusted R^2.
When deciding upon the inclusion of a variable, the following criteria are commonly used:
A - Theory: Theoretical justification is often considered to include a variable in a model. It involves assessing whether the variable is relevant and aligns with the underlying theory or conceptual framework.
B - t-statistic: The t-statistic is used to determine the statistical significance of a variable. A variable with a significant t-statistic suggests that it has a meaningful relationship with the dependent variable and may be included in the model.
C - Bias: Bias refers to the presence of systematic errors in the estimation of model parameters. It is important to consider the potential bias introduced by including or excluding a variable and assess whether it aligns with the research objectives.
D - Adjusted R^2: Adjusted R^2 is a measure of the goodness of fit of a regression model. It considers the trade-off between the number of variables included and the overall fit of the model. Adjusted R^2 helps in assessing whether the inclusion of a variable improves the model's explanatory power.
To know more about variable visit:
brainly.com/question/29583350
#SPJ11
What is the vertex of f(x)=x^2−12x+25 ?
Answers
Answer:
vertex is (6, -11)
Step-by-step explanation:
Given equation
f(x) = x² - 12x + 25
is that of an upward-facing parabola(since the coefficient of x² is positive).
The vertex will be at a minimum and its x-coordinate can be found by finding the first derivative of f(x), setting it equal to zero and solving for x
f'(x) = d/dx(x² - 12x + 25)
= 2x - 12
f'(x) = 0 ==> 2x - 12 = 0
2x = 12
x = 6
Substitute x = 6 in f(x) to get
f(6) = 6² - 12(6) + 25
= 36 - 72 + 25
= -11
So the vertex is at (6, -11)
Ruben and his friends are celebrating Ruben's birthday at Adventure Zone, which has trampolines, mini golf, laser tag, and an arcade. Ruben's mom gives 18 arcade tokens to each kid at the party. In all, she gives out 144 tokens.
Use an equation to find the number of kids at Ruben's party.
Answers
The number of kids that are at Ruben's party will be 8 kids.
Let the number of kids at the party be represented by x.Number of arcades token given to each person = 18Total number of arcade tokens given out = 144Based on the information given, the equation to solve the question will be:
18 × x = 144
18x = 144
x = 144/18
x = 8
Therefore, there are 8 kids at the party.
Read related link on:
https://brainly.com/question/25294118
Snefuru’s north pyramid at Dahshur, Egypt, is shown. It’s square base has a side length of 220 m. The height of the pyramid is 105 m. Determine it’s surface area.
The answer is 115,324 m^2, show how you got your answer please. :))
Answers
Answer: 115,324 m^2
Step-by-step explanation:
To find the surface area, we need height of the triangle face of the pyramid. We are given the height of the pyramid itself (105 m). To find the height of the triangle face, we have to use the Pythagorean theorem (a^2 + b^2 = c^2).
In the diagram attached, the height of the triangle face is the hypotenuse of the blue triangle: 110^2 + 105^2 = c^2 where c = about 152 m (ROUNDED)
Now that we have the height of the triangle face, we can use the triangle area formula: 1/2(base)(height) to find the area of one of the triangle faces.
1/2 (220)(152) = 16,720 m^2
Since there are four triangle faces, we need to multiply this number by four.
16,720(4) = 66880 m^2.
Now we just have to add this to the area of the square base which is:
(220)(220) = 48400 m^2
66880 + 48400 = 115,200 m^2 (which is very close to the answer provided - if 152 wasn't rounded, 115,324 would be your answer)

dagogo uploads 333 videos on his channel every month. each video averages 151515 minutes in length and gets an average of 150{,}000150,000150, comma, 000 new views. the average ratio of likes-to-views of dagogo's videos is 1:51:51, colon, 5. dagogo wants to reach a total of 9{,}000{,}0009,000,0009, comma, 000, comma, 000 views on his channel. assuming these rates continue, how many likes does dagogo get, on average, for each minute of video he uploads?
Answers
In linear equation, For 20 Months Dagogo requires to upload videos to get 90,000,000 views on his channel.
What in mathematics is a linear equation?
A linear equation is a first-order (linear) term plus a constant in the algebraic form y=mx+b, where m is the slope and b is the y-intercept.
The variables in the previous sentence, y and x, are referred to as a "linear equation with two variables" at times.
Dagogo uploads 3 videos on his channel each month.
Each video gets an average of 1500000 views.
3 Video get Views = 3 * 1500000
= 4,500,000 Views
Views per month = 4,500,000 Views
Total Views = 90,000,000 views
Number of months = Total Views/Views per month
Number of months = 90,000,000/4,500,000
Number of months 20 Months
For 20 Months Dagogo requires to upload videos to get 90,000,000 views on his channel.
Learn more about linear equation
brainly.com/question/11897796
#SPJ4
The complete question is -
Dagogo uploads 3 videos on his channel every month. Each video averages 15 minutes in length and gets an average of 150,000 new views. The average ratio of likes-to-views of Dagogo videos is 1:5. Dagogo wants to reach a total of 9,000,000 views on his channel. Assuming these rates continue, for how many months does Dagogo need to upload videos to get to 9,000,000 views on his channel?
Answer:
2000 likes per minute
Step-by-step explanation:
If each video averages 15 minutes and he gets an average of 150000 new views, we can divide.
150000/15=10000
If the ratio of likes to views is 1:5, we can assume 10000 is the "5" and divide it by 5.
10000/5=2000
2000:10000 = 1:5
2000 likes per minute
(KHAN)
Suntract ( p-q)-(p+q)
Answers
The answer is -2q
hope this helps <3
Determine the minimal number of stages of a shift register
necessary for generating following sequence 0 1 0 1 0 1 1 0.
Answers
Hence, a shift register with a minimum of 8 stages would be necessary to generate the given sequence.
To determine the minimal number of stages of a shift register necessary for generating the given sequence, we need to find the length of the shortest feedback shift register (FSR) capable of generating the sequence.
Looking at the sequence 0 1 0 1 0 1 1 0, we can observe that it repeats after every 8 bits. Therefore, the minimal number of stages required for the shift register would be equal to the length of the repeating pattern, which is 8.
To know more about shift register,
https://brainly.com/question/30618034
#SPJ11
What is the output of the function f(x) = x^2 + 1, when the input is 6? Can someone really help me out on this please i will really thank youuu..
Answers
Answer:
37
Step-by-step explanation:
Since the input is 6, you plug it in as the x value to get y.
The input=x value
the output=y value
This is because when you input an x-value into an equation, you would get its y value.
So... 6^2 is 36 and 36+1 is 37
So the final answer is 37
A triangle has sides with length of 12 miles 16 miles 20 miles
Is it a right triangle

Answers
Answer:
Yes! This is a right triangle.
Step-by-step explanation:
To solve this problem, you need to use the Pythagorean Theorem, which is: \(a^2+b^2=c^2\). In this equation, "A" represents the smallest length, "B" represents the next smallest length, and "C" represents the largest length. If a triangle is a right triangle, then the A squared + B squared equals C squared.
In this equation:
A = 12
B = 16
C = 20
1. Insert the values: \(12^2+16^2=20^2\)
2. Simplify: \(144+256=400\)
\(144+256=400\), and \(20^2=400\), so this is a right triangle.
Hope this helps! Please feel free to give Brainliest if you feel this helped. :)

Answer:
it is a right triangle, solve using the pythagorean theorem.
Simplify \(\frac{sec(a)-csc(a)}{sec(a)+csc(a)}\)
Answers
The simplified version of (sec a - cosec a) / (sec a + cosec a) is cosec 2a(cosec 2a - 2) / (sec²a - cosec²a).
What is trigonometry?The study of correlations between triangles' side lengths and angles is known as trigonometry. The field was created in the Hellenistic era in the third century BC as a result of the use of geometry in astronomical research.
Given:
(sec a - cosec a) / (sec a + cosec a)
Multiply the numerator and denominator by (sec a - cosec a)
(sec a - cosec a) / (sec a + cosec a) × (sec a - cosec a)
(sec²a + cosec²a -2sec a cosec a) / (sec²a - cosec²a)
As we know,
\(sec^2a + cosec^2a = sec^2a \ cosec^2a\)
sec² a cosec² a - 2sec a cosec a / (sec²a - cosec²a)
sec a cosec a (sec a cosec a - 2) / (sec²a - cosec²a)
cosec 2a(cosec 2a - 2) / (sec²a - cosec²a)
To know more about trigonometry:
https://brainly.com/question/14272510
#SPJ1
Which equation can you use to calculate the
missing credit score?
*-780
1.07
28
x - 28
780=
1.07
28 =
x-1.07
780
Answers
Answer:
1.07=x-780/28
Step-by-step explanation:
Miss credit score: 810
Answer:
810
Step-by-step explanation:
determine whether the series is absolutely convergent, conditionally convergent, or divergent. 4 7 4 · 10 7 · 9 4 · 10 · 16 7 · 9 · 11 4 · 10 · 16 · 22 7 · 9 · 11 · 13
Answers
To determine whether the series is absolutely convergent, conditionally convergent, or divergent, we can use the Ratio Test. Answer : the series is divergent.
Let's analyze the given series:
4, 7, 4 · 10, 7 · 9, 4 · 10 · 16, 7 · 9 · 11, 4 · 10 · 16 · 22, 7 · 9 · 11 · 13, ...
We will calculate the ratio of consecutive terms:
(7/4), (40/7), (63/40), (352/63), (1386/352), (7722/1386), ...
Now, we will calculate the limit of the absolute value of the ratios:
lim(n->∞) |a(n+1)/a(n)| = lim(n->∞) |(7722/1386) / (1386/352)| = lim(n->∞) |(7722/1386) * (352/1386)| = lim(n->∞) |7722/1386 * 352/1386| = |2039328/1933156| = 1.055...
The limit of the absolute value of the ratios is greater than 1. According to the Ratio Test, if the limit is greater than 1, the series diverges. Therefore, the given series is divergent.
In conclusion, the series is divergent.
Learn more about limit : brainly.com/question/12211820
#SPJ11
This shape is made up of one half-circle attached to an equilateral triangle with side lengths 20 inches. You can use 3. 14 as an approximation for π
Answers
If the shape is made up of one half-circle attached to an equilateral triangle with side lengths 20 inches then, the perimeter of the shape is 91.4 inches.
To find the perimeter of the shape, we need to know the length of the curved boundary (the circumference of the half-circle) and the length of the straight boundary (the perimeter of the equilateral triangle).
The radius of the half-circle is half the length of the side of the equilateral triangle, which is 10 inches. Therefore, the circumference of the half-circle is:
C = πr = π(10) = 31.4 inches.
The perimeter of the equilateral triangle is 3 times the length of one side, which is 20 inches. Therefore, the perimeter of the triangle is:
P = 3s = 3(20) = 60 inches
Finally, the perimeter of the entire shape is the sum of the lengths of the curved and straight boundaries:
Perimeter = C + P = 31.4 + 60 = 91.4 inches.
To know more about equilateral triangle
brainly.com/question/3461022
#SPJ4
Complete Question
This shape is made up of one half-circle attached to a square with side lengths 11 inches. Find the perimeter of the shape.
You can use 3.14 as an approximation for π. help i don't know it.
Jamal owns a parking garage and is trying to find the relationship between hour of the day and number of cars in the garage. He finds that between 4 am and 10 am he can model this with a linear relationship. The equation for this model is y = 3. 56x + 2. How many cars were in the garage at 4 am?.
Answers
The slope of the equation, given, is the pace at which a car enters a garage. Hence, it is 3.56, or around 4 automobiles per hour. Option D is the correct answer.
In statistics, a straight line of correlation between two variables is referred to as a linear relationship (or linear association). The mathematical equation y = mx + b can be used to represent linear relationships graphically.
Jamal is the owner of a parking garage and is attempting to determine the correlation between the number of automobiles in the garage and the hour of the day. He discovers that he can represent this using a linear relationship between 4 am and 10 am. y = 3.56x + 2 is the model's equation.
To learn more about a linear relationship
https://brainly.com/question/11663530
#SPJ4
The complete question of the above answer is
Jamal owns a parking garage and is trying to find the relationship between the hour of the day and the number of cars in the garage. He finds that between 4 am and 10 am he can model this with a linear relationship. The equation for this model is y = 3.96x + 2. About how many cars are entering the garage every hour?
A) 1
B) 2
C) 3
D) 4
Simplify (-5)^4•[(-5)²]5• (-5)^4
![Simplify (-5)^4[(-5)]5 (-5)^4](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/audxy03XiIlVl5Ct00M4Z5T8vIGKKvmi.png)
Answers
Answer:
\((-5)^{4}.[(-5)^{2}]^{5}.(-5)^{4}=(-5)^{4}.(-5)^{10}.(-5)^{4}=(-5)^{18}\)
Step-by-step explanation:
Answer:
(-5)^18
Step-by-step explanation:
The equation will look like this after you simplify[(-5)^2)^5]
(-5)^4 x (-5)^10 x (-5)^4
Now you add up all the exponents and keep it the same:
(-5)^18
Hope this helps!
copy the incomplete axes and fill in the missing number so that the scaling is consistent.
2-137 only help me

Answers
Answer:
A: write0,4,8,12,16,20 on the line which the answer for A is 16 divided by 4=4
B: Write 0,25,50,75,100,125,150 on the line which the answer for B is 50 divided by 2= 25
Margo participated in a surfing competition. During the competition, the height of the ocean waves increased from two feet to six feet. a. Identify how many times greater the amount of energy carried by the six-foot wave was than the amount of energy caried by the two-foot wave. Explain your reasoning.
Answers
Answer:
three times the two foot wave wuold be the six foot wave
Step-by-step explanation:
because its right
The London Eye is a large Ferris wheel that has diameter 135 meters and revolves continuously. Passengers enter the cabins at the bottom of the wheel and complete one revolution in about 27 minutes. One minute into the ride a passenger is rising at 0.06 meters per second. How fast is the horizontal motion of the passenger at that moment?
Answers
Answer:
0.253 m/s
Step-by-step explanation:
You want to know the horizontal component of motion of a passenger riding a Ferris wheel when they are 1/27 of the way around the circle and their rate of rise is 0.06 m/s.
Angle of elevationThe wheel makes one revolution in 27 minutes, so the angular displacement is changing at the rate of (360°)/(27 min) = 13 1/3°/min.
After 1 minute, the passenger is following a path that has an angle of elevation of 13 1/3°.
Horizontal componentThe ratio of vertical speed to horizontal speed will be the tangent of the angle of elevation:
Vv/Vh = tan(13 1/3°)
Then the horizontal speed will be ...
Vh = Vv/tan(13 1/3°) = (0.06 m/s)/0.237004
Vh ≈ 0.253 m/s
The passenger's horizontal motion is about 0.253 m/s.
A pair of new shoes were originally $75, but I got them during the sale for 20% off. If the tax in my area is 8.25% , how much did I spend in all ?
Answers
You spent $64.95 or $65
Step-by-step explanation:
As per given conditions,
\(75 \times (8.25 \: percent+ 1) \times (1 - 20 \: percent)\)
\( = > 75 \times( \frac{8.25}{100} + 1) \times (1 - \frac{20}{100}) \)
\( = > 75 \times (0.0825 + 1) \times (1 - 0.2)\)
\( = > 75 \times 1.0825 \times 0.8\)
\( = > 64.95\)
If you round off to the nearest, then you get $65
~Benjemin360