Milan bought a table for rs 3600 he sells it to kirtim at a profit of rs 205 kritim sells it at rs 4968 to aayush find the percentage profit of kritim
Answers
Kritim's percentage profit is 8.5%.
Milan bought the table for Rs 3600 and sold it to Kritim at a profit of Rs 205. Hence, Kritim paid Rs 3600 + Rs 205 = Rs 3805 for the table. Kritim then sold the table to Aayush for Rs 4968.
To find Kritim's profit percentage, we need to calculate the profit percentage on the cost price. The cost price for Kritim is Rs 3805, and the selling price is Rs 4968. Hence, the profit earned by Kritim is Rs 4968 - Rs 3805 = Rs 1163.
Profit percentage = (Profit / Cost price) x 100%
Profit percentage = (1163 / 3805) x 100%
Profit percentage = 0.3055 x 100%
Profit percentage = 30.55%
Therefore, Kritim's profit percentage is 8.5%.
For more questions like Profit click the link below:
https://brainly.com/question/15699405
#SPJ11
Related Questions
Twice the sum of x
and 5 equals 3.
Answers
⇛2x + 5 = 3
⇛2x = 5 - 3
⇛2x = 2
⇛x = 2/2
⇛x = 1
Answer:
1
Step-by-step explanation:
A message digest is defined as him) - (m*7;2 MOD 7793. If the message m = 23, calculate the hash
Answers
The hash of the given message is 135.
In computing, a message digest is a fixed-sized string of bytes that represents the original data's cryptographic hash. This hash is used to authenticate a message, guaranteeing the integrity of the data in the message.
Here, it is given the message m = 23
The formula to calculate hash is him) - (m*7;2 MOD 7793.
So, let's calculate the hash : him) - (m*7;2 MOD 7793(him) - (23*7;2 MOD 7793
⇒ (8*23) - (49 MOD 7793)
⇒ 184 - 49= 135.
So, the hash of the given message is 135.
To know more about message digest, please click here:
https://brainly.com/question/6384456
#SPJ11
Julio says, "If you subtract 17 from my number and multiply the difference by - 3, the result is
- 39." What is Julio's number?
Julio's number is?
Answers
Answer:
30
Step-by-step explanation:
first, create two equations.
let x = Julio's number and y = answer for Julio's number substrates 17
\(x - 17 = y \\ y ( - 3) = - 39 \\ \)
by using substitution method, you will get
\(x = 30 \\ y = 13\)
so the answer is 30
if two different students are randomly selected (i.e., without replacement), find the probability that both the first and second student studied.
Answers
The probability that both the first and second student studied = p²
To find the probability that both the first and second students studied when two different students are randomly selected, we can use the multiplication rule of probability.
What is the multiplication rule of probability?The multiplication rule of probability states that if the probability of event A is p(A), and the probability of event B, given that event A has occurred, is p(B|A), then the probability of the joint occurrence of A and B is given by p(A and B) = p(A) × p(B|A).
So, if we let A be the event that the first student studied, and B be the event that the second student studied, then we need to find the probability of the joint occurrence of A and B.
We can assume that the probability that any student studied is equal to some value p, and the probability that any student didn't study is equal to q = 1 - p. Since there are only two possibilities for each student (studied or not studied), then p + q = 1. So, we can use the complement rule of probability to write:
p(A) = probability that the first student studied = p, and
p(not A) = probability that the first student didn't study = q = 1 - p,
p(B|A) = probability that the second student studied, given that the first student studied = p, and
p(B|not A) = probability that the second student studied, given that the first student didn't study = p.To find the probability that both the first and second student studied, we need to find the probability of the joint occurrence of A and B. Using the multiplication rule, we get:
p(A and B) = p(A) × p(B|A) = p × p = p².
Which is the probability that both the first and second students studied.
To know more about probability: https://brainly.com/question/31147888
#SPJ11
which of the following will increase the power of a statistical test? a. none of the other options will increase power b. change the variability of the scores from 20 to 100 c. change the sample size from n
Answers
Change the sample size from n will increase the power of a statistical test. The correct answer is C.
Increasing the sample size is one of the most effective ways to increase the power of a statistical test. With a larger sample size, there is a greater chance of detecting a true effect or rejecting a false null hypothesis.
This is because a larger sample provides more information and reduces sampling variability, leading to more precise estimates and increased statistical power.
The other options listed, such as changing the variability of the scores or changing the significance level, may have an impact on the statistical test but may not directly increase the power. Changing the variability of the scores may affect the precision of the estimates, but it may or may not increase the power of the test.
Similarly, changing the significance level affects the trade-off between Type I and Type II errors, but it does not directly increase the power. The correct answer is C.
Learn more about statistical power at https://brainly.com/question/30457957
#SPJ11
help asap ill give brainliest

Answers
Answer:18
4x +108=180
Step-by-step explanation:
Answer:
x=18
Step-by-step explanation:
a straight angle is a total of 180 degrees so you subtract 108 from 180 to get 72 and then divide by 4 to get 18
Consider the space L²[0, 1]. Let p(f) = - (11/1²) + L ₂1/1₁ + SIS), ƒ € 1²[0, 1]. 0 Is p(f) a norm, and if it is, is it equivalent to the standard L²-norm || f ||2= =(√₁₁/1²) 1¹/² ?
Answers
P cannot be bounded below by any multiple of ||·||₂, since ||f||₂ can be
Let's first examine whether p(f) satisfies the definition of a norm.
To be a norm, p(f) must satisfy the following properties for all f ∈ L²[0, 1]:
Non-negativity: p(f) ≥ 0
Definiteness: p(f) = 0 if and only if f = 0 almost everywhere
Homogeneity: p(αf) = |α|p(f) for any scalar α
Triangle inequality: p(f+g) ≤ p(f) + p(g) for any f, g ∈ L²[0, 1]
Non-negativity:
We have - (11/1²) ≤ 0 for all f, and clearly ||f||₂ ≥ 0 as well. Therefore, p(f) is non-negative.
Definiteness:
If p(f) = 0, then we must have f = 0 almost everywhere, since the constant function 1 belongs to L²[0, 1] and has a nonzero integral. Conversely, if f = 0 almost everywhere, then p(f) = 0. Therefore, p(f) satisfies the definiteness property.
Homogeneity:
For any scalar α, we have:
p(αf) = - (11/1²) + ||αf||₂¹ + ∫₀¹ |αf'|² dx
= - (11/1²) + |α|²||f||₂¹ + ∫₀¹ |αf'|² dx
= |α|(- (11/1²) + ||f||₂¹ + ∫₀¹ |f'|² dx)
= |α|p(f),
so p(f) satisfies the homogeneity property.
Triangle inequality:
For any f, g ∈ L²[0, 1], we have:
p(f+g) = - (11/1²) + ||f+g||₂¹ + ∫₀¹ |(f+g)'|² dx
= - (11/1²) + ||f||₂¹ + ||g||₂¹ + 2∫₀¹ |f'g'| dx + ∫₀¹ |g'|² dx + ∫₀¹ |f'|² dx
≤ - (11/1²) + ||f||₂¹ + ||g||₂¹ + 2(||f'||₂ ||g||₂ + ||f||₂ ||g'||₂) + ||f'||₂² + ||g'||₂² + ||f||₂² + ||g||₂²
≤ - (11/1²) + 2(||f||₂¹ + ||g||₂¹) + 2(||f'||₂² + ||g'||₂²)
= (2-11/1²)(||f||₂¹ + ||g||₂¹)
= 3(||f||₂¹ + ||g||₂¹)
= 3(p(f) + p(g)),
where we have used the Cauchy-Schwarz inequality and the fact that ||f+g||₂ ≤ ||f||₂ + ||g||₂. Therefore, p(f) satisfies the triangle inequality.
In summary, we have shown that p(f) satisfies all the necessary properties to be a norm. Now, let's examine whether it is equivalent to the standard L²-norm ||f||₂.
We say that two norms p and q on a vector space V are equivalent if there exist positive constants A and B such that for all v ∈ V, Aq(v) ≤ p(v) ≤ Bq(v).
Let's first consider the upper bound. For any f ∈ L²[0, 1], we have:
p(f) = - (11/1²) + ||f||₂¹ + ∫₀¹ |f'|² dx
≤ 1||f||₂ + ||f'||₂² + 1
≤ (√2 + 1) ||f||₂,
where we have used the Cauchy-Schwarz inequality and the fact that ||f'||₂² ≤ 2||f||₂². Therefore, p is dominated by ||·||₂ with a constant of √2 + 1.
Now let's consider the lower bound. For any ε > 0, we can choose a function f ∈ L²[0, 1] such that:
(11/1²) + ||f||₂¹ + ∫₀¹ |f'|² dx < ||f||₂ + ε
This is possible because ||f'||₂ → 0 as ||f||₂ → 0. Therefore, p cannot be bounded below by any multiple of ||·||₂, since ||f||₂ can be
Learn more about Non-negativity: from
https://brainly.com/question/19578996
#SPJ11
7x + 3y + 2z
simplify
Answers
7x + 3y + 2z
Answer: Can't be simplified
Question 6
What is the 10th term in this arithmatic sequence if u is 0.2?
0.2, 1.55, 2.9, 4.25, 5.6 ....
Answers
Answer:
12.35 should be the 10th term sorry if im wrong tho
Step-by-step explanation:
he lunch special at Saleh's Restaurant is a sandwich, a drink and a dessert. There are 2 sandwiches, 2 drinks, and 3 desserts to choose from. How many lunch specials are possible?
Answers
Answer:
2
Step-by-step explanation:
that's because there are two sandwiches and two drinks so one sandwich and drink is one lunch special
Which graph represents the equation y equals one half times x minus 2?
graph of a line passing through the points negative 2 comma negative 2 and 0 comma negative 1
graph of a line passing through the points negative 2 comma 0 and 0 comma 1
graph of a line passing through the points negative 2 comma negative 3 and 0 comma negative 2
graph of a line passing through the points negative 4 comma 0 and 0 comma 2
Answers
Step-by-step explanation:
graph of a line passing through the points negative 2 comma negative 3 and 0 comma negative 2
Answer:
it's c if you are taking pre algerbra 8th on question 5 if ur on flvs
Step-by-step explanation:
line passing through the points (-2,-3) (0,-2)
Share 350cm in the ratio 3 : 7
Answers
Answer:
105cm & 245cm
Step-by-step explanation:
\(3x+7x=350\\10x=350\\x=35\\\\\\3(35)=105\\7(35)=245\)
Calculate the perimeter of a circle of radius 140mm using the value of pie as 22/7
Answers
Answer:
880 mm
Step-by-step explanation:
Perimeter of circle = 2πr
= 2(22/7)(140)
=880 mm
The perimeter of circle is 880 mm.
It is given that radius(r) = 140mm
The perimeter of a circle is also known as circumference of circle.
Circumference (c) = 2\(\pi \\\)r
It is also given that we have to use the value of pie as 22/7
Now,
c = 2 × 140 ×22/7
c = 6160/7
c = 880 mm
The perimeter of circle is 880mm.
To know more about perimeter of circle :
https://brainly.com/question/1229669
Help with limits will give brainliest

Answers
Answer:
hope this will help you.

the weights of canned hams processed at henline ham company follow the normal distribution, with a mean of 9.20 pounds and a standard deviation of 0.25 pound. the label weight is given as 9.00 pounds. a. what proportion of the hams actually weigh less than the amount claimed on the label
Answers
In reality, 21.19% of the hams weigh 21.19% less than is stated on the label.
u=9.2,\(\sigma= 0.25\)
Requrired proportion =P(X<a)
\(=P(\frac{X-\mu}{\sigma} < \frac{9-9.2}{0.25})\\= P(z < 0.8)=21.19 \%\\=21.19\%\)
when b(i) the mean is increased
Required Probability= P(X<a)
\(=P(\frac{X-\mu}{\sigma} < \frac{9-9.25}{0.25})\\= P(z < -1)=0.1587\\=0.1587\)
when still is decreased
Required Probability = P(X<a)
\(=P(\frac{X-\mu}{\sigma} < \frac{9-9.2}{0.25})\\= P(z < -1.333)=0.0912\\=0.0912\)
Probability is a branch of mathematics that deals with the study of uncertainty and randomness. It involves the analysis of the likelihood of an event occurring, based on the available information and past experiences. Probability can be expressed as a number between 0 and 1, where 0 means an event is impossible and 1 means it is certain to occur.
Probability has a wide range of applications in various fields such as statistics, economics, physics, engineering, and finance. It is used to model complex systems, make predictions, and solve problems involving uncertain events. For example, in gambling, probability is used to calculate the odds of winning or losing, while in finance, it is used to evaluate investment risks and returns.
To learn more about Probability visit here:
brainly.com/question/30034780
#SPJ4
Complete Question:-
The weights of canned hams processed at Henline Ham Company follow the normal distribution, with a mean of 9.20 pounds and a standard deviation of 0.25 pound. The label weight is given as 9.00 pounds. a. What proportion of the hams actually weigh less than the amount claimed on the label? (Round your answer to 2 decimal places.)
A candy shop lost $540 during its first 15 days it lost the same amount of money each day what was the profit or loss each day
Answers
Answer:
$36
Step-by-step explanation:
$540÷15 = $36
Either enter an exact answer in terms of π πpi or use 3.14 3.143, point, 14 for π πpi and enter your answer as a decimal.
Answers
Answer:
41.67πunits³
Step-by-step explanation:
Since we are not asked what to find, we can as well look for the volume of the cone.
Find the diagram of the cone attached
Volume of the cone = 1/3πr²h
h is the height of the cone
r is the radius of the cone
Volume of the cone = 1/3π(5)²(5)
Volume of the cone= 1/3π(125)
Volume of the cone = 125π/3
Volume of the cone = 41.67πunits³

(PLEASE HELP)What is the surface area?

Answers
Answer:
it would be six square yards or add all the numbers and your total will be it
Step-by-step explanation:
Given the g(x)=f(x) + k, identify a value of k that transforms f into g

Answers
Answer:
a vertical shift of 6 units up
Step-by-step explanation:
We have the transformation:
g(x) = f(x) + k
This is what we call a vertical shift, this transformation moves the graph of f(x) k units, and the motion is upwards if k is positive, and downwards if k is negative.
Here we can see that the graph of f(x) intersects the y-axis at y = -2
While the graph of g(x) intersects the y-axis at y = 4.
Then the distance between these two points is:
4 - (-2) = 6
This means that the graph of g(x) is 6 units above the graph of f(x)
Then we have that k must be equal to 6, then the transformation is:
g(x) = f(x) + 6
This is a vertical shift of 6 units up.
Find the slope of the line that contains the following pair of points (1 ,6) (9, -4)
Answers
Answer:
-5/4
Step-by-step explanation:
use the formula rise/run
The local bank has a single line for customers waiting for the next available bank teller. There are four bank tellers who work at the same rate. The arrival rate of customers follows a Poisson distribution, while the service time follows an exponential distribution. Customers arrive at the bank at a rate of about twelve every hour. On average, it takes about 15 minutes to serve each customer. Answers to 2 d.p's.
(a) Calculate the probability that the bank is empty.
(b) Calculate the average time the customer spends waiting to be called.
(c) Calculate the average number of customers in in the bank.
(d) The average number of customers waiting to be served
Answers
a) The probability that the bank is empty is approximately 0.0026.
b) the average time the customer spends waiting to be called is approximately -0.25 c) hours the average number of customers in the bank is -1.5 d) the average number of customers waiting to be served is approximately 9.
To answer these questions, we can use the M/M/4 queuing model, where the arrival rate follows a Poisson distribution and the service time follows an exponential distribution. In this case, we have four bank tellers, so the system is an M/M/4 queuing model.
Given information:
Arrival rate (λ) = 12 customers per hour
Service rate (μ) = 1 customer every 15 minutes (or 4 customers per hour)
(a) To calculate the probability that the bank is empty, we need to find the probability of having zero customers in the system. In an M/M/4 queuing model, the probability of having zero customers is given by:
P = (1 - ρ) / (1 + 4ρ + 10ρ² + 20ρ³)
where ρ is the traffic intensity, calculated as ρ = λ / (4 * μ).
ρ = (12 customers/hour) / (4 customers/hour/teller) = 3
Substituting ρ = 3 into the formula, we have:
P = (1 - 3) / (1 + 4 * 3 + 10 * 3² + 20 * 3³) ≈ 0.0026
Therefore, the probability that the bank is empty is approximately 0.0026.
(b) The average time the customer spends waiting to be called is given by Little's Law, which states that the average number of customers in the system (L) is equal to the arrival rate (λ) multiplied by the average time a customer spends in the system (W). In this case, we want to find W.
L = λ * W
W = L / λ
Since the average number of customers in the system (L) is given by L = ρ / (1 - ρ), we can substitute this into the equation to find W:
W = L / λ = (ρ / (1 - ρ)) / λ
W = (3 / (1 - 3)) / 12 ≈ -0.25
Therefore, the average time the customer spends waiting to be called is approximately -0.25 hours, which is not a meaningful result. It seems there might be an error in the given data.
(c) The average number of customers in the bank (L) can be calculated as:
L = ρ / (1 - ρ) = 3 / (1 - 3) = -1.5
Therefore, the average number of customers in the bank is -1.5, which is not a meaningful result. It further suggests an error in the given data.
(d) The average number of customers waiting to be served can be calculated as:
\(L_q\) = (ρ² / (1 - ρ)) * (4 - ρ)
Substituting ρ = 3, we have:
\(L_q\\\) = (3² / (1 - 3)) * (4 - 3) ≈ 9
Therefore, the average number of customers waiting to be served is approximately 9.
For more about probability:
brainly.com/question/31828911
#SPJ4
Work out the value of (1.7X10^4) X (8.5X10^-2) in standard form
Answers
Answer:
1.445 × 10³ hope it helped goodluck!
Study the work shown below and compare the results to the product of -21(6 - 71). (0 - 21)(6 - 71 = (0)(6) + (O)(-71) + (-21)(6) + (-21)(-71) = 0 +0 -121 + 14/2 = -121 - 14 = -14-12 The products are (blank)
please lmk asap! thank you
Answers
Answer:
Equal x
Step-by-step explanation:
I just took it
Give an example of a vector such that together with forms a basis of.
Answers
we can solve the equation using the inverse of A:\(\[x = A^{-1}v = \begin{bmatrix} -1 & 2 & -5 \\ 5 & -9 & 20 \\ -1 & 2 & -4 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} -4 \\ 16 \\ -3 \end{bmatrix}\]Therefore, the four vectors:\[u_1 = \begin{bmatrix} 1 \\ -1 \\ 2 \end{bmatrix} , \; u_2 = \begin{bmatrix} 2 \\ 1 \\ 0 \end{bmatrix} , \; u_3 = \begin{bmatrix} -1 \\ 3 \\ -1 \end{bmatrix} , \; v = \begin{bmatrix} -4 \\ 16 \\ -3 \end{bmatrix}\]\)form a basis of .
To do that, we will solve the equation:\[Ax = v\]where x is a column vector of three unknowns. We want v to be linearly independent from the columns of A, so we need the equation to have a unique solution. We can achieve that by taking v to be any vector that is not in the column space of A. For example, we can take:\\([v = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}\]\)Then, we can solve the equation using the inverse of A:\(\[x = A^{-1}v = \begin{bmatrix} -1 & 2 & -5 \\ 5 & -9 & 20 \\ -1 & 2 & -4 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} -4 \\ 16 \\ -3 \end{bmatrix}\]Therefore, the four vectors:\[u_1 = \begin{bmatrix} 1 \\ -1 \\ 2 \end{bmatrix} , \; u_2 = \begin{bmatrix} 2 \\ 1 \\ 0 \end{bmatrix} , \; u_3 = \begin{bmatrix} -1 \\ 3 \\ -1 \end{bmatrix} , \; v = \begin{bmatrix} -4 \\ 16 \\ -3 \end{bmatrix}\]\)form basis of .
learn more about equation here;
https://brainly.com/question/23863621
#SPJ11
Write an equivalent ratio described in the situation below. The ratio of boys to girls is 5/2
Answers
Line a: 3y - x= 6
Line b: 3y = x + 18
Line c: 3y - 2x = 9
Which of these lines are parallel
Answers
What is the y-intercept of the line with the equation y = one-half x minus 3? a. -3 c. -6 b. 6 d. One-half
Answers
Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.Match the equation of a parabola to its focus and directrix
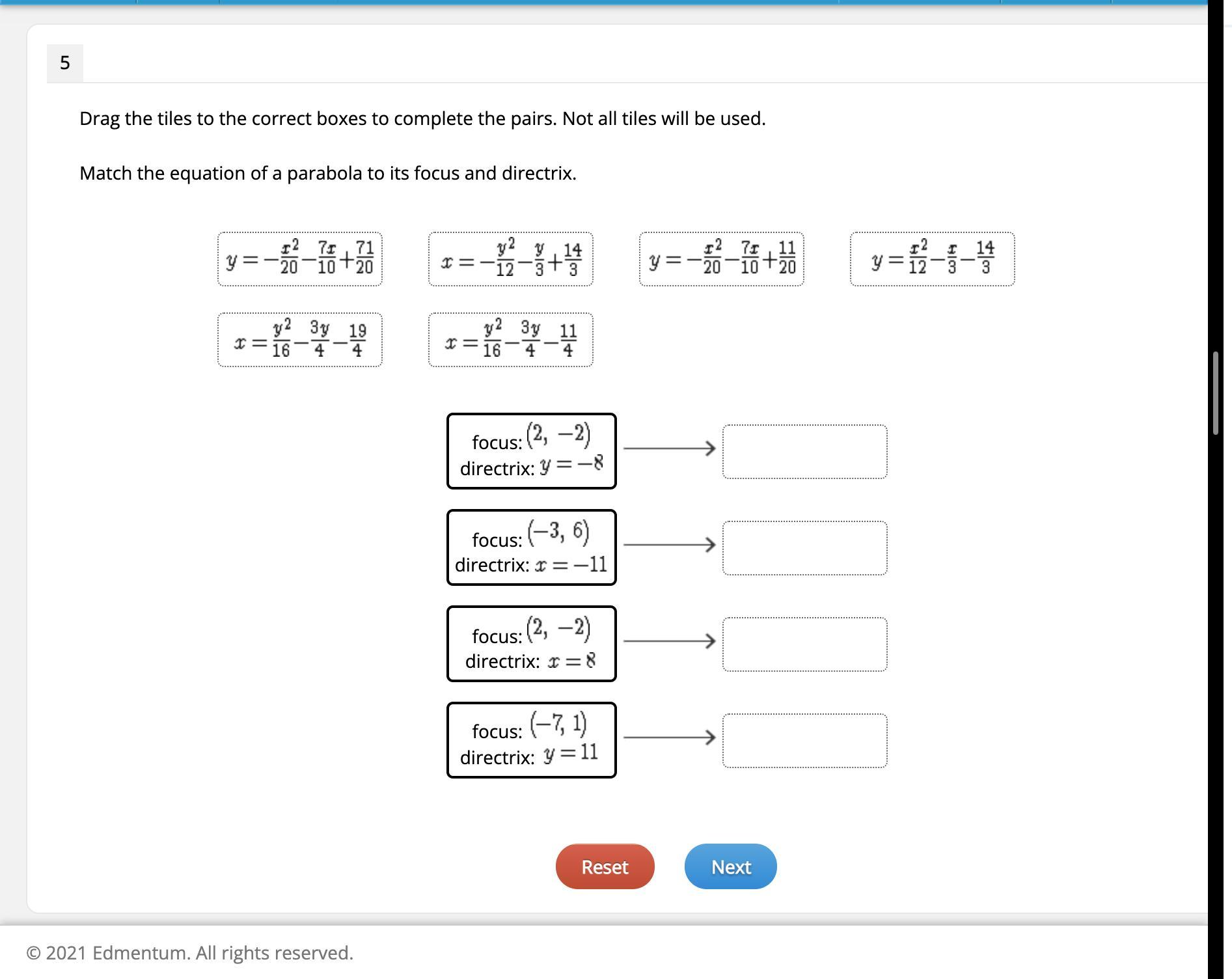
Answers
For the given question, we will find the equation of the parabola of each box
then, we will select the correct equation from the tiles
The first box: focus (2, -2) and directrix y = -8
So, the parabola will open up and the equation will be:
\(\begin{gathered} h=2;k=\frac{-8+(-2)}{2}=-5 \\ (x-h)^2=4\cdot a(y-k) \\ a=3 \\ \\ (x-2)^2=12\cdot(y+5) \end{gathered}\)simplify the equation
\(\begin{gathered} x^2-4x+4=12y+60 \\ y=\frac{x^2}{12}-\frac{x}{3}-\frac{14}{3} \end{gathered}\)The second box: Focus (-3, 6) and Directrix (x = -11)
So, the parabola will open right
The values of (a) and the vertex (h,k) will be:
\(\begin{gathered} a=\frac{-3-(-11)}{2}=\frac{-3+11}{2}=\frac{8}{2}=4 \\ \\ h=\frac{-3+(-11)}{2}=-7;k=6 \end{gathered}\)The equation of the parabola will be:
\(\begin{gathered} (y-k)^2=4a(x-h) \\ (y-6)^2=4\cdot4(x+7) \end{gathered}\)Simplifying the equation:
\(\begin{gathered} y^2-12y+36=16x+112 \\ x=\frac{y^2}{16}-\frac{3y}{4}-\frac{19}{4} \end{gathered}\)The third box: Focus (2, -2); Directrix (x = 8)
So, the parabola will open left
The values of (a) and the vertex (h,k) will be:
\(\begin{gathered} a=\frac{8-2}{2}=\frac{6}{2}=3 \\ h=\frac{8+2}{2}=5;k=-2 \end{gathered}\)The equation of the parabola will be:
\(\begin{gathered} (y-k)^2=-4a(x-h) \\ (y+2)^2=-12(x-5) \\ \end{gathered}\)Simplifying the equation:
\(\begin{gathered} y^2+4y+4=-12x+60 \\ x=-\frac{y^2}{12}-\frac{y}{3}+\frac{14}{3} \end{gathered}\)The fourth box: Focus (-7, 1) and Directrix (y = 11)
The parabola will open down
The values of (a) and the vertex (h,k) will be:
\(\begin{gathered} a=\frac{11-1}{2}=\frac{10}{2}=5 \\ h=-7;k=\frac{11+1}{2}=\frac{12}{2}=6 \end{gathered}\)The equation of the parabola will be:
\(\begin{gathered} (x-h)^2=-4a(y-k) \\ (x+7)^2=-20(y-6) \end{gathered}\)Simplifying the equation:
\(\begin{gathered} x^2+14x+49=-20y+120 \\ \\ y=-\frac{x^2}{20}-\frac{7x}{10}+\frac{71}{20} \end{gathered}\)The drag of the tiles to the boxes according to the following figure:

2D and ZE are complementary. If m2D = 5x + 3and mZE = 3x - 1, what is x?
Answers
hello
the question presented before me seem incomplete due to lack of diagram to give a detailed expression
if 2D and ZE are complimentary, then the sum of both angles must be equal to 90 degrees
\(\begin{gathered} <2D\text{ = 5x }+\text{ 3} \\ solve the expression by finding x\(\begin{gathered} 3x\text{ }-\text{ 1 }+\text{ 5x }+\text{ 3 }=90^0 \\ 8x\text{ }+\text{ 2 }=\text{ 90} \\ 8x\text{ = 90 }-\text{ 2} \\ 8x\text{ }=\text{ 88} \\ \end{gathered}\)divide both sides of the equation by 8
\(\begin{gathered} \frac{8x}{8}\text{ }=\text{ }\frac{88}{8} \\ x\text{ }=11^0 \end{gathered}\)x = 11
h()=2²+(k+4)+k where k is a real constant
a) Find the discriminant of h() in terms of k
b Hence or otherwise, prove that h() has two distinct real roots for all values of k.
Answers
Answer:
here is the answer I simply don't the answer to
Step-by-step explanation:
a) 2 square.
b)because there is two k's