Michael starts a new paper company. The function fff models the company's net worth (in thousands of dollars) as a function of time (in months) after Michael starts it. A company is in debt if its net worth is negative. Plot the point on the graph of fff that corresponds to the first time after 666 months at which the company is no longer in debt.
Answers
Answer:
is 0,14
Step-by-step explanation:
i promise
The x-intercept of a function is when \(y =0\). The question is incomplete, as the function that models the company's net worth is not given. So, I will provide a general solution.
See attachment for the graph of the assumed function.
For this solution, we make use of the following representations
\(x \to\) month
\(y \to\) net worth
The company is out of debt when the net worth is not negative. The scenario is represented as: \(y \ge 0\)
This means that we set the y-value to a non-negative value, and then calculate the x-value.
In this case, the y-value to use will be \(y=0\) ---- This represents the first point when the company is not in debt.
Assume the function is:
\(y = 5x - 15\) ----- This is just an assumption (Replace this with function in the complete question)
The solution will be:
\(0 = 5x - 15\)
Collect like terms
\(5x = 15\)
Divide by 5
\(x = 3\)
So, the first point when the company is no longer in debt will be: (3,0)
Also note that the above point represents the x-intercept of the function
See attachment for the graph of the assumed function.
Read more about x-intercepts at:
https://brainly.com/question/3520400

Related Questions
Get the formula for cos(6θ) and sin(6θ) by utilizing de Moivre's theorem. Moivre's theorem is given as (cosθ+isinθ) n
=cos(nθ)+isin(nθ) 2. Solve for the possible values of i i
. Show all steps involving the solution on how to get the possible values of i i
.
Answers
The formulas for cos(6θ) and sin(6θ) using de Moivre's theorem are:
cos(6θ) = Re[(cosθ + isinθ)^6]
sin(6θ) = Im[(cosθ + isinθ)^6]
To find the formulas for cos(6θ) and sin(6θ) using de Moivre's theorem, we can start by expressing (cosθ + isinθ) raised to the power of 6. According to de Moivre's theorem, this can be written as (cos(6θ) + isin(6θ)).
Expanding (cosθ + isinθ)^6 using the binomial theorem, we get:
(cosθ + isinθ)^6 = C(6, 0)(cosθ)^6(isinθ)^0 + C(6, 1)(cosθ)^5(isinθ)^1 + C(6, 2)(cosθ)^4(isinθ)^2 + C(6, 3)(cosθ)^3(isinθ)^3 + C(6, 4)(cosθ)^2(isinθ)^4 + C(6, 5)(cosθ)^1(isinθ)^5 + C(6, 6)(cosθ)^0(isinθ)^6
Simplifying this expression, we can calculate each term separately. The terms with odd powers of isinθ will be imaginary and will contribute to sin(6θ), while the terms with even powers of isinθ will be real and will contribute to cos(6θ). After evaluating the terms and combining like terms, we obtain the formulas for cos(6θ) and sin(6θ).
Learn more about de Moivre's theorem.
brainly.com/question/28999678
#SPJ11
Round 1sf 0.48x1594.3
Answers
Answer:
800
Step-by-step explanation:
0.48 x 1594.3 = 765.264
765.264 rounded to 1sf = 800
Answer:
there that the solution
Step-by-step explanation:
and solution

What is meant by a system of linear equations?
Answers
HELP ASAP
What is the distance, in units, between the points \((-3, -4)\) and \((4, -5)\)? Express your answer in simplest radical form.
Answers
Answer:
d=5√2 unit
Step-by-step explanation:
distance between two points d=√(x2-x1)²+(y2-y1)²
two pints (-3,-4) and (4,-5)
d=√(4-(-3)²+(-5-(-4)²
d=√(4+3)²+(-5+4)²
d=√49+1
d=√50
d=√25*2
d=5√2
Answer
\( \boxed{5 \sqrt{2} \: \: \:units}\)
Step by step explanation
Let the points be A and B
A ( - 3 , - 4 ) ⇒( x₁ , y₁ )
B ( 4 , - 5 )⇒( x₂ , y₂ )
Now, let's find the distance between these points :
Distance = \( \mathsf{ \sqrt{ {(x2 - x1)}^{2} + {(y2 - y1)}^{2} } }\)
Plug the values
⇒\( \mathsf{ \sqrt{ {(4 - ( - 3))}^{2} + {( - 5 - ( - 4))}^{2} } }\)
Calculate
⇒\( \mathsf{ \sqrt{ {(4 + 3)}^{2} + {( - 5 + 4)}^{2} } }\)
⇒\( \mathsf{ \sqrt{ {(7)}^{2} + {( - 1)}^{2} } }\)
Evaluate the power
⇒\( \mathsf{ \sqrt{49 + 1} }\)
Add the numbers
⇒\( \mathsf{ \sqrt{50} }\)
Simplify the radical expression
⇒\( \mathsf{5 \sqrt{2} \: \: units}\)
Hope I helped!
Best regards!!
What is the value of f?

Answers
Answer:
f(1/2) = -2
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Function NotationStep-by-step explanation:
Step 1: Define
f(x) = 8x - 6
f(1/2) is x = 1/2
Step 2: Evaluate
Substitute in x: f(1/2) = 8(1/2) - 6Multiply: f(1/2) = 4 - 6Subtract: f(1/2) = -2The driving distance between Manchester and London is 195 miles. Farris wants to travel from Manchester to London on coach. The coach will leave Manchester at 3:30pm. Farris assumes the coach will travel at an average speed of 50mph. work out Farris's arrival time in London?
Answers
Answer:
7:24 pm
Step-by-step explanation:
speed = distance/time
time * speed = distance
time = distance/speed
time = (195 miles)/(50 miles/hour)
time = 3.9 hours
The trip will take 3.9 hours.
3 hours + 0.9 hours = 3 hours + 0.9 hours * 60 minutes/hour =
= 3 hours + 54 minutes
The trip will take 3 hours and 54 minutes.
3:30 pm + 3:54 = 6:84 pm = 7:24 pm
Answer: 7:24 pm
under what conditions is it permissible to proceed with a hypothesis test, even though the assumption that participants are randomly selected is violated?
Answers
it may be permissible to proceed with a hypothesis test even if the assumption of random participant selection is violated, under the conditions of known and accounted for non-random selection or random assignment to treatment groups
Random participant selection is an important assumption in hypothesis testing, as it helps ensure the generalizability of the results to the target population. However, in some situations, it may be impractical or impossible to achieve perfect random selection. In such cases, there are a few conditions under which it may still be permissible to proceed with a hypothesis test despite the violation of this assumption:
Non-random selection is known and accounted for: If the non-random selection process is well-documented and understood, researchers can adjust their analysis or statistical methods to account for potential biases introduced by the non-random selection.
Random assignment to treatment groups: Even if participants are not randomly selected, random assignment to different treatment groups can help mitigate the impact of non-random selection. By randomly assigning participants to treatment groups, the effects of non-random selection are distributed evenly across the groups, allowing for valid comparisons and hypothesis testing.
Learn more about participant selection here:
https://brainly.com/question/14862285
#SPJ11
Select the values that are solutions to the inequality x2 + 3x – 4 > 0. –6 –2 0 5
Answers
The values that are solutions to inequality are -6 and 5.
Options A and D are the correct answer.
What is inequality?It shows a relationship between two numbers or two expressions.
There are commonly used four inequalities:
Less than = <
Greater than = >
Less than and equal = ≤
Greater than and equal = ≥
We have,
x² + 3x - 4 > 0
Now,
Substituting x = -6, -2, 0, 5
(-6)² + 3(-6) - 4 > 0
36 - 18 - 4 > 0
36 - 22 > 0
14 > 0
True.
x² + 3x - 4 > 0
(-2)² + 3 x (-2) - 4 > 0
4 - 6 - 4 > 0
-6 > 0
This is not true.
x² + 3x - 4 > 0
0 + 3 x 0 - 4 > 0
0 + 0 - 4 > 0
-4 > 0
This is not true.
x² + 3x - 4 > 0
5² + 3 x 5 - 4 > 0
25 + 15 - 4 > 0
40 - 4 > 0
36 > 0
This is true.
Thus,
-6 and 5 are the solutions to inequality.
Learn more about inequalities here:
https://brainly.com/question/20383699
#SPJ1
Write an equation in slope-intercept form of the line shown.

Answers
Answer:
Step-by-step explanation:
y2-y1/x2-x1
1+3
3-1
your slope is 4/2 or 2. keep going down to find what y is when x is 0, which happens to be -5
so now you have a slope and a y intercept you can solve like y=mx+b where m is your slope and B is your y intercept
y=2x-5 is your answer
Kamal’s goal was to save $180 for a trip.
In the first week, Kamal saved $26 from his allowance and $34 from his job. He spent $6 for lunch one day and another $3 on the bus.
Hana said, Kamal will be able to save $54 in the first week.
a- Is Hana correct? What error did she make?
Answers
Answer:
Hana is wrong
Step-by-step explanation:
savings=26+34
=60
savings left after spending=60-6-3
=51
What is the equation of the line which passes through the point (-1,2) and is parralel to the line y = x + 4
Answers
Step-by-step explanation:
y = mx+ c
y = x + 4
m = 1
Parallel means m1 = m2
and we know that (-1, 2) = (x, y)
y - y1 = m (x - x1)
y - 2 = 1 (x + 1)
y - 2 = x + 1
y = x + 1 + 2
y = x + 3
#CMIIWAnswer
\(\large\textrm{y = x + 3}\)
Further explanation
We know the slope of the line, it's 1.
How did I figure this out?The given equation is in slope-intercept form: y = mx + b, in which x and y are the co-ordinates of the point which the line passes through and m and b are the slope and y-intercept, respectively.
Also the slopes of parallel lines are always the same.
So 1 is the slope.
Basically, we know m but we don't know b, so let's go ahead and find it.
Plug in 2 for y:
\(2=x+b\)
Plug in -1 for x:
\(2=-1+b\)
We have a little equation that we can solve in terms of b:
\(-1+b=2\)
\(b=2+1\)
\(b=3\)
The y-intercept is 3; that makes the line's equation y = x + 3.
Show that the problem of determining the satisfiability of boolean formulas in disjunctive normal form is polynomial-time solvable.
Answers
that the problem of determining the satisfiability of boolean formulas in disjunctive normal form (DNF) is indeed polynomial-time solvable.
DNF is a form of boolean expression where the expression is a disjunction of conjunctions of literals (variables or negations of variables). In other words, the DNF expression is true if any of the conjunctions are true.
To determine the satisfiability of a DNF formula, we need to find whether there exists an assignment of true or false to each variable such that the entire expression evaluates to true. One way to do this is by using the truth table method, which involves evaluating the expression for all possible combinations of true/false values for the variables.
However, this method becomes computationally expensive for large DNF formulas with many variables. A more efficient way to solve this problem is by using the Quine-McCluskey algorithm, which reduces the DNF formula to a simplified form that can be easily checked for satisfiability.
determining the satisfiability of boolean formulas in DNF is polynomial-time solvable due to the availability of efficient algorithms such as the Quine-McCluskey algorithm.
To learn more about polynomial visit:
https://brainly.com/question/11536910
#SPJ11
How can we use the distributive property to find an expression equivalent to 15(x+2)?
Answers
Answer:
\(15x + 30\)
Step-by-step explanation:
To simplify the given expression, we have to use the distributive property.
This means that we have to 'distribute', meaning multiply, each of the values inside the parentheses with the number outside the parentheses.
∴ \(15(x+2)\)
⇒ \((15 \times x ) + (15 \times 2)\)
⇒ \(15x + 30\)
Therefore, the resulting equivalent expression is: \(15x + 30\).
Learn more about the distributive property here:
https://brainly.com/question/27543580
State the equation of the graphed function.

Answers
The equation of the graphed function is given as follows:
f(x) = x³ + 2x² - 5x - 6.
How to obtain the equation of the function?
The equation of the function is obtained considering the Factor Theorem, as a product of the linear factors of the function.
From the graph, the zeros of the function are:
x = -3.x = -1.x = 2.Hence the function is:
f(x) = a(x + 3)(x + 1)(x - 2).
In which a is the leading coefficient.
Expanding the product, we have that:
f(x) = a(x² + 4x + 3)(x - 2)
f(x) = a(x³ + 2x² - 5x - 6).
When x = 0, y = -6, hence the leading coefficient a is obtained as follows:
-6a = -6
a = 1.
Hence the function is:
f(x) = x³ + 2x² - 5x - 6.
More can be learned about functions at https://brainly.com/question/24808124
#SPJ1
4(x + 3) + 2(x − 4) Expanded and simplified
Answers
Answer:
\(\huge\boxed{\sf 6x + 4}\)
Step-by-step explanation:
Given expression:= 4(x + 3) + 2(x - 4)
Distribute 4 to (x + 3) and 2 to (x - 4)= 4x + 12 + 2x - 8
Combine like terms= 4x + 2x + 12 - 8
= 6x + 4\(\rule[225]{225}{2}\)
4(x + 3) + 2 (x - 4)
4x + 4 x 3 + 2x - 2 x 4
4x + 12 + 2x - 8
6x + 4
Segment JK has endpoints J(2,4) and K(6,2). You dilate the segment using a dilation centered at the origin with a scale factor of 1/2 and then reflect the image over the x-axis. Where is the final image of K?

Answers
The final image of K would be at (3,-1) after the given sequence of transformation Segment JK.
What is Dilation?Dilation is a process for creating similar figures by changing the size.
Segment JK has endpoints J(2,4) and K(6,2).
A dilation by a factor of 1/2 means that each coordinate value will be multiplied by 1/2.
The dilation of segment JK with a scale factor of 1/2 would shrink the segment by half, so the coordinates of K would be (3,1).
Reflecting over the x-axis would change the sign of the y-coordinate, so the final image of K would be at (3,-1).
Learn more about the Dilation here:
brainly.com/question/13176891
#SPJ1
How many four-letter sequences are possible that use the letters b, r, j, w once each? sequences
Answers
There are 24 possible four-letter sequences using the letters b, r, j, and w once each.
To find out how many four-letter sequences are possible using the letters b, r, j, and w once each, we can use the formula for permutations of n objects taken r at a time, which is:
P(n,r) = n! / (n-r)!
In this case, n = 4 (since there are 4 letters to choose from) and r = 4 (since we want to choose all 4 letters). So we can plug in these values and simplify:
P(4,4) = 4! / (4-4)!
P(4,4) = 4! / 0!
P(4,4) = 4 x 3 x 2 x 1 / 1
P(4,4) = 24
Learn more about permutation here: brainly.com/question/30649574
#SPJ11
(3^6-3^8)/(9^4 -9^2)
Answers
Answer:
Step-by-step explanation:
First, let's simplify the numerator:
3^6 - 3^8 = 729 - 6561 = -5832
Now, let's simplify the denominator:
9^4 - 9^2 = 6561 - 81 = 6480
So, the expression simplifies to:
(-5832) / 6480 = -0.9
78 is 65% of what number?
Answers
Answer:
120
Step-by-step explanation:
Answer: 120
Step-by-step explanation: hope this helps
As part of a community service project at your highshcool you are organizing a fund raiser at the neighborhood movie theater money raised will benefit a summer camp for children with special needs the admission charge is 10.00 per person, 5.50 of which is used to pay the movie theaters rental fee, the remainder is donated to the summer camp fund what are the two variables involved in this problem
Answers
Answer:
Yes it is a function. It passes the vertical line test. In other words, it is impossible to draw a single vertical line through more than one point on the V shaped graph. Any input leads to exactly one output.
The domain is the set of all real numbers. This is because we can plug in any x value leading to some specific y value. There are no holes or gaps or jumps to indicate we must restrict any given x value. The domain would not be the set of whole numbers only because values between the whole numbers (eg: decimal values like x = 2.75) work just fine.
The range is the set of y values such that y is either 0 or larger than 0. In short, the range is . Notice how any point on the V shaped graph has a y coordinate that is either 0 or larger than 0. It is impossible to get a y value that is negative.
Step-by-step explanation:
Quick help please it will mean a lot if you help me :)
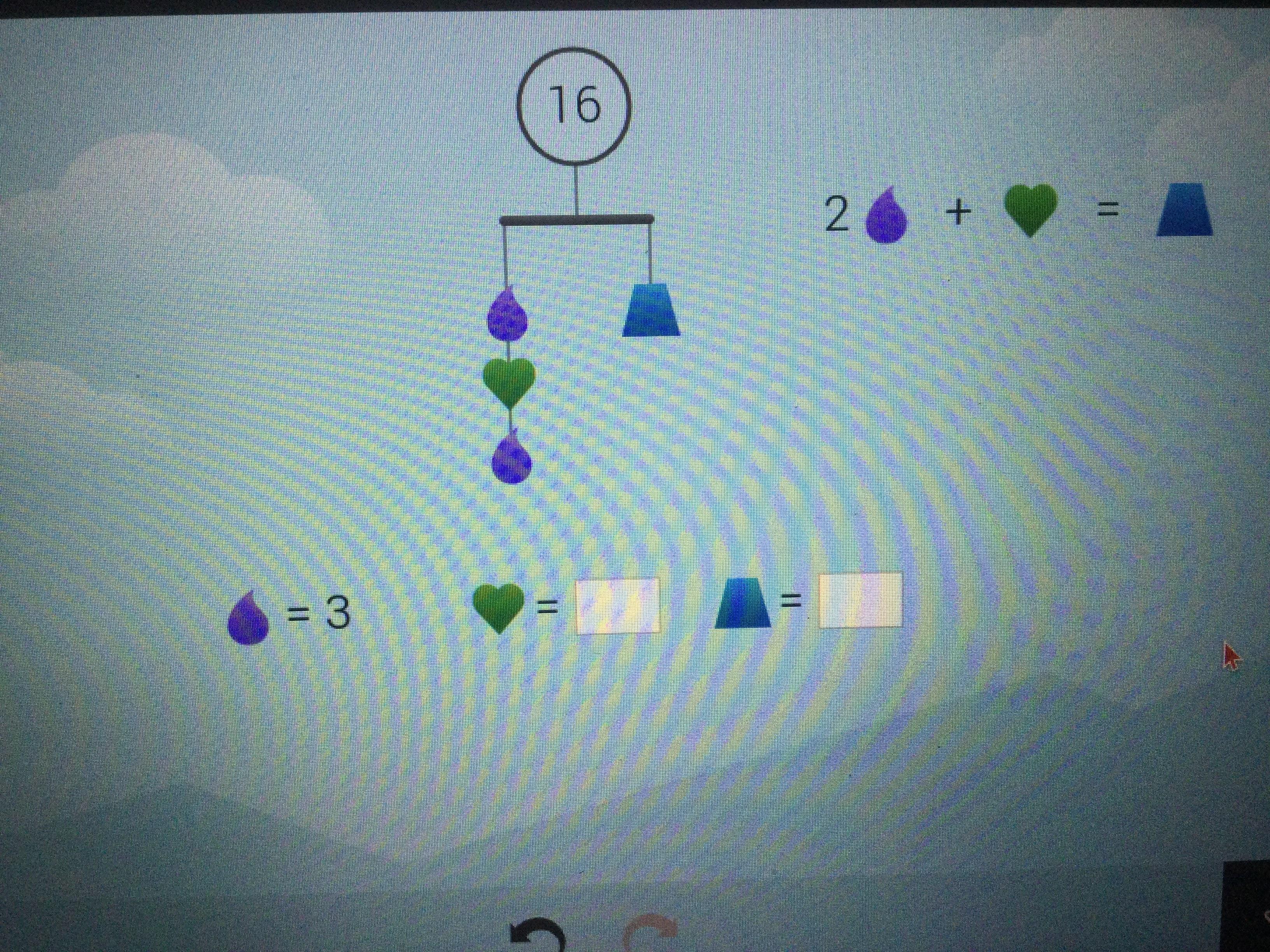
Answers
Answer:
Green heart is 2 and blue shape is 8.
Step-by-step explanation:
We know 1 purple drop equals 3.
So 3+3 = 6
The total weight is 16 so we can do 16-6 = 10
We have 10 left. Since we need the weight to be balanced the green heart must be 2.
Because then it would be 8 on 1 side (2 purples equals 6 and 1 heart equals 2, so 6+2=8) and 8 on the other side (8+8=16).
Suppose that f(x) is differentiable for all x and that 2 ≤ f'(x) ≤ 5. If f(-3) = -1, use the Mean Value Theorem to determine the largest and smallest possible values of f(4). [6] 2. For f(x) = 3x¹ + 4x³, determine the critical points and then determine the intervals of increase and decrease. Use the intervals of increase and decrease to classify any [7] critical points as being local maxima/minima or neither.
Answers
After considering the given data we conclude that the answer for the sub questions are
a) the smallest possible value of f(4) is -1 + 7(2) = 13, and the largest possible value of \(f(4) is -1 + 7(5) = 34\).
b) Since f'(x) is defined for all x, there are no critical points where f'(x) does not exist.
c) Therefore, the critical points are local maxima at x = -1/2 and x = 1/2.
a) To determine the largest and smallest possible values of f(4) using the Mean Value Theorem, we need to find a number c in the interval (-3,4) such that \(f'(c) = (f(4) - f(-3))/(4 - (-3)).\) Since f(x) is differentiable for all x and \(2 \leq f'(x) \leq 5\), we know that \(14 \leq 7f'(c) \leq 35\). Rearranging the equation, we get \(f(4) = f(-3) + 7f'(c)\). Substituting f(-3) = -1, we get \(f(4) = -1 + 7f'(c).\) Therefore, the smallest possible value of f(4) is -1 + 7(2) = 13, and the largest possible value of \(f(4) is -1 + 7(5) = 34.\)
b) For \(f(x) = 3x^1+ 4x^3\), we need to find the critical points and determine the intervals of increase and decrease. Taking the derivative of f(x), we get \(f'(x) = 3 + 12x^2\). Setting f'(x) = 0, we get \(3 + 12x^2 = 0\), which gives \(x =\pm \sqrt(1/4) = \pm1/2.\) Since f'(x) is defined for all x, there are no critical points where f'(x) does not exist.
c) To determine the intervals of increase and decrease, we can use the first derivative test. Since \(f'(x) = 3 + 12x^2 > 0 for x < -1/2 and x > 1/2\), f(x) is increasing on (-∞,-1/2) and (1/2,∞). Since f'(x) < 0 for -1/2 < x < 1/2, f(x) is decreasing on (-1/2,1/2).
Therefore, the critical points are local maxima at x = -1/2 and x = 1/2.
To learn more about Mean Value Theorem
https://brainly.com/question/30403137
#SPJ4
−8/9⋅5/6 pls only correct answers. will give 30 points
Answers
Answer:
- 20/27
Step-by-step explanation:
Answer:
Exact Form: 20 /27
List the values from least to greatest 5/12, 0.416, 42%, which is the middle value?
HELP.
Answers
I decided to put them as decimals. 5/12 is equivalent to 0.416. Then there is a decimal already there, which is also 0.416. Then there is 42% which as a decimal is 0.42.
In order it is
0.416, 0.416, and 0.42
The first two are equivalent :P
Answer: 0.416, 5/12, 42%
The middle value is 5/12
Step-by-step explanation: I converted all of them into decimals, so it would be easier to compare. (5/12=0.41666667) (0.416=0.416) (42%=0.42)
If you want me to show you how to convert into decimals just let me know.
.let f be differentiable function such that f(3) = 2 and f'(3) = 5. if the tangent line to the graph of f at x = 3 is used to find an approximaton to a zero of f, that approximation is:
a) .4
b) .5
c) 2.5
d) 3.4
e) 5.5
Answers
The approximation to a zero of the function f using the tangent line at x = 3 is 2.5 (option c).
When we have a differentiable function and we know the value of the function and its derivative at a specific point, we can use the tangent line at that point to approximate zeros of the function.
In this case, the function f has a tangent line at x = 3, and we know that the function value f(3) is 2 and the derivative f'(3) is 5.
The tangent line has the same slope as the derivative at that point, so its slope is 5. The equation of the tangent line can be written as: y - f(3) = f'(3)(x - 3)
Plugging in the values we know, we have: y - 2 = 5(x - 3)
Simplifying the equation, we get: y = 5x - 13
To find the zero of the function, we set y equal to zero and solve for x: 0 = 5x - 13
5x = 13
x = 13/5
So the approximation to a zero of the function f using the tangent line at x = 3 is 2.6, which is closest to 2.5 (option c).
To know more about derivative click here
brainly.com/question/29096174
#SPJ11
Please help school is ending soon!
Two days later, Kelly surveyed the same 13 classmates and found that none of them had been given math homework since she last surveyed them. By how much does the mean of Kelly’s second data set change in comparison with the mean of the data set in her original survey? Explain how to determine the change in the means without calculating the mean of either data set.


Answers
Since none of the 13 classmates had been given math homework between the original survey and Kelly's second survey, the sum of the values in the second data set is the same as the sum of the values in the original data set. Therefore, the change in the means can be determined without calculating the mean of either data set by considering the number of data points in each set.
Since both data sets have the same number of data points, the change in the means will be zero. This is because the mean is calculated by dividing the sum of the values by the number of data points, and since the sum of the values is the same in both data sets, the means will also be the same.
In other words, if the mean of the first data set is x, then the sum of the values in the first data set is 13x (since there are 13 classmates), and the sum of the values in the second data set is also 13x (since none of the values have changed). Therefore, the mean of the second data set will also be x, and the change in the means will be zero.
The following cards were dealt from a shuffled standard deck of cards:
spades: 3, 4, 6, j, q, k
clubs: a, 2, 5, 7, j, k
hearts: a, 2, 5
diamonds: a, 2, 3, 6, k
based on the dealt cards, what is the empirical probability of dealing a black card?
a.
25%
b.
40%
c.
50%
d.
60%
Answers
The empirical probability of dealing with a black card is 40%.
Define probability.Probability is a branch of mathematics that deals with numerical representations of the likelihood of an event occurring or of a proposition being true. The probability of an occurrence is a number between 0 and 1, with 0 approximately denoting impossibility and 1 denoting certainty. An event's probability grows with its possibility of happening. Tossing a fair (impartial) coin provides a simple demonstration.
Given
The dealer draws a total of 20 cards for this question—8 black cards and 12 red cards.
The likelihood of dealing with a black card is the subject of the question.
Given that the probability just asks for the color, you can disregard the card number. The likelihood would be,
Black card/Total card
8/12+8
8/20
2/5
0.4
40%
The empirical probability of dealing a black card is 40%.
To learn more about probability, visit:
https://brainly.com/question/8137713
#SPJ4
Answer: 40%
Step-by-step explanation:
I got it right on edmentum
what are the ordered pairs of the solutions for this system of equations?
f(x)=x^(2)-2x+3; f(x)=-2x+12

Answers
The ordered pairs for the system of equations f(x) = x^2 -2x + 3 and f(x) = -2x + 12 are (3, 6) and (-3, 18)
What is a quadratic equation?A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term. The first condition for an equation to be a quadratic equation is the coefficient of x2 is a non-zero term(a ≠ 0)
f(x) = x^2 -2x +3 and f(x) = -2x + 12
which means
x^2 -2x +3 = -2x + 12
x^2 -2x +3 + 2x - 12 = 0
x^2 -9 = 0
by factorizing we have
(x-3)(x+3) = 0
x = 3 or -3
when x = 3
f(x) = -2x + 12
f(3) = -2(3) + 12 which is 6
when x = -3
f(-3) = -2(-3) + 12 which is 18
ordered pairs are (3, 6) and (-3, 18)
In conclusion, (3, 6) and (-3, 18) are the ordered pairs
Learn more about Quadratic equation: https://brainly.com/24334139
#SPJ1
Write an equation for the line of best fit and then predict how much money travelers will spend in 2008. a. y = 2 x 380; travelers will spend about $410 billion in the year 2008. b. y = 2 x 320; travelers will spend about $350 billion in the year 2008. c. y = 20 x 320; travelers will spend about $620 billion in the year 2008. d. y = 20 x 380; travelers will spend about $680 billion in the year 2008.
Answers
The line of the equation should be y = 20x + 320 and travelers will spend about $620 billion in the year 2008. So, the option c is correct.
In the given question, we have to write an equation for the line of best fit and then predict how much money travelers will spend in 2008.
The graph of the question is given below:
From the graph the points are (1.5, 350) and (4, 400)
As we know that the formula of the equation of line is:
y-y(1) = {y(2)-y(1)}/{x(2)-x(1)} (x-x(1))
x(1) = 1.5, y(1) = 350, x(2) = 4 and y(2) = 400
Now putting the values
y-350 = (400-350)/(4-1.5) (x-1.5)
y-350 = 50/2.5 (x-1.5)
y-350 = 20(x-1.5)
y-350 = 20x-30
Add 350 on both side, we get
y = 20x + 320
So, the line of the equation should be y = 20x + 320.
So that travelers will spend about $620 billion in the year 2008.
Hence, the option c is correct.
To learn more about line of the equation link is here
brainly.com/question/21511618
#SPJ4

Circle O has a circumference of approximately 250π ft. Circle O with diameter d is shown. What is the approximate length of the diameter, d? 40 ft 80 ft 125 ft 250 ft
Answers
Answer:
250 ft
Step-by-step explanation:
circumference of circle 'C' is defined as
C = 2πr
250π = 2πr
r = 250π/2π
r= 125
d = 2r = 2×125 = 250 .
diameter of the given circle is 250 ft
The diameter of the circle is 250ft
Data;
Circumference = 250πdiameter = dCircumference of a CircleThe formula of circumference of a circle is given as
\(c = 2\pi r\)
Let's substitute the values in here and solve
\(c = 2 \pi r\\250\pi = 2 \pi r\\r = 125ft\)
The length of the radius is 125ft
But the length of diameter of a circle is twice the length of the radius
\(d = 2r\\d = 2 * 125\\d = 250ft\)
The diameter of the circle is 250ft
Learn more on circumference of a circle here;
https://brainly.com/question/14283575