Marianne had 128 brood cows. She lost 2 cows and calves during calving and 3 calves were born dead. She had 4 cows that did not calve.a. What percent of the cows was lost? Express your answer to the nearest tenth of a percent.b. How many calves does she have?c. What percent of the cows have a calf at their side? Express your answer to the nearest tenth of a percent.
Answers
Marianne had 128 brood cows. She lost 2 cows and calves during calving and 3 calves were born dead. She had 4 cows that did not calve.
a. What percent of the cows was lost? Express your answer to the nearest tenth of a percent.
b. How many calves does she have?
c. What percent of the cows have a calf at their side? Express your answer to the nearest tenth of a percent.
Part a
total original cows=128 ------> represent 100%
so
Applying proportion
Find out how much percentage represent 2 cows
100/128=x/2
solve for x
x=(100/128)*2
x=1.6%
Part b
total cows=128-2=126
total calves=126-3-4=119 calves
Part c
total cows=126
total cows that have a calf at their side=119
applying proportion
100/126=x/119
solve for x
x=(100/126)*119
x=94.4%
Related Questions
I've spent 1 hour on two separate days trying to understand this problem. Calc professor isn't being helpful at all either. Any help is appreciated!

Answers
Answer:
\(f(x)=-log_{3}(-x)\)
Step-by-step explanation:
Based on the points given on the graph, I would say this is a Log function, reflected across both x- and y-axes.
And given the point (-3, -1), it must be \(-log_{3}(-x)\)
For any positive integer n, the value of n! is the product of the first n positive integers. For example, 4! = 4 * 3 * 2 * 1 =24. What is the greatest common divisor of 5! and 7! ?
Answers
The GCD of 5! and 7! is 2^3 * 3^1 * 5^1 = 120.
the greatest common divisor of 5! and 7! is 120.
To find the greatest common divisor (GCD) of 5! and 7!, we need to factorize both numbers and identify the common factors.
First, let's calculate the values of 5! and 7!:
5! = 5 * 4 * 3 * 2 * 1 = 120
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5,040
Now, let's factorize both numbers:
Factorizing 120:
120 = 2^3 * 3 * 5
Factorizing 5,040:
5,040 = 2^4 * 3^2 * 5 * 7
To find the GCD, we need to consider the common factors raised to the lowest power. In this case, the common factors are 2, 3, and 5. The lowest power for 2 is 3 (from 120), the lowest power for 3 is 1 (from 120), and the lowest power for 5 is 1 (from both numbers).
For more such question on greatest common divisor
https://brainly.com/question/219464
#SPJ8
Which of the following relations represents y as a function of x?
A. {(2,2), (2,3), (2,4), (2,5)}
B. {(0,1), (-7,1), (0,6), (8,1)}
C. {(2,6), (3,6), (5,-2), (3,8)}
D. {(1,2), (2,3), (5,3), (7,9)}
Answers
Answer:
The correct answer is D
Step-by-step explanation:
In a function, none of the x values in the set can be repeating. D is the only option that meets this requirement.
What are the y-intercept of the function f(x)=-2x^2-3x+20?

Answers
Answer:
\(\sf A) \ (-4, \ 0) \ and \ \ [\dfrac{5}{2} , \ 0]\)
Explanation:
Given function: f(x) = -2x² - 3x + 20
To find the x-intercepts of a function, f(x) = 0
=================
-2x² - 3x + 20 = f(x)
-2x² - 3x + 20 = 0
-2x² - 8x + 5x + 20 = 0
-2x(x + 4) + 5(x + 4) = 0
(-2x + 5) (x + 4) = 0
-2x + 5 = 0, x + 4 = 0
-2x = -5, x = -4
x = -5/-2,x = -4
x = 5/2, x= -4
Coordinates: (-4, 0), (5/2, 0)

Which word should replace the question mark (?) in the
equation below?
?
-
mass
acceleration
Please help

Answers
Answer:
speed I'm pretty sure sorry if its wrong
Answer:
Force
Step-by-step explanation:
Newton's second law of motion is F = ma, or force is equal to mass times acceleration.
Convert the given radian measure to a degree measure.
Negative 1.7 pi
it is -306
Answers
Answer:
The answer is correct: radians -1.7pi is -306 °
2p² - 3 = 15 | What is the value
Answers
Answer: p= -3
p=-5/2=-2.500
Step-by-step explanation:
plss be brianleist
Please help if you can, this is due tomorrow.
In the diagram below, $\angle BAC=24^\circ$ and $AB=AC$.
If $\angle ABC=y^\circ$, what is the value of $y$?
[asy]
size(4.25cm);
pair a=(0,cos(pi/15)); pair b=(-sin(pi/15),0); pair c=-b; pair d=c+(1,0);
dot(a); dot(b); dot(c);
draw(c--a--b--c);
draw((2*a+3*b)/5-0.05*(cos(pi/15),-sin(pi/15))--(2*a+3*b)/5+0.05*(cos(pi/15),-sin(pi/15)));
draw((2*a+3*c)/5-0.05*(cos(pi/15),sin(pi/15))--(2*a+3*c)/5+0.05*(cos(pi/15),sin(pi/15)));
label(scale(0.75)*"$24^\circ$",a-(0,0.3),S);
label("$A$",a,N);
label("$B$",b,SSW);
label("$C$",c,S);
label(scale(0.85)*"$y^\circ$",b,NE);
[/asy]
Answers
The given diagram implies that the triangle $ABC$ is an isosceles triangle with angles of $24^\circ$. This can be verified by computing the length of the hypotenuse and using the Pythagorean Theorem.
What is equation?Equation is a mathematical expression that consists of variables, symbols, and numbers, and shows the relationship between different quantities. An equation can involve one or more unknowns, and can be represented as an equality or as an inequality. Solving an equation requires understanding the relationship between the different elements in the equation, and manipulating the equation to isolate the unknowns. Common types of equations include linear equations, quadratic equations, and polynomial equations.
From this diagram, we can conclude that $\angle ABC$ is an isosceles triangle. This is because the angles opposite equal sides of a triangle must be equal. Since $\angle BAC=24^\circ$, $\angle ABC$ must be $24^\circ$. Furthermore, the sides $AB$ and $AC$ are equal, so $ABC$ is an isosceles triangle.
This conclusion can be verified by using the Pythagorean Theorem. If $AB=AC$, then it follows that $BC = \sqrt{AB^2 + AC^2} = \sqrt{2AB^2}$. Since $AB=3$, it follows that $BC=\sqrt{2*3^2}=6$. Therefore, the triangle $ABC$ is a right triangle with legs of length 3 and hypotenuse of length 6. Since $\angle BAC = 24^\circ$, it follows that $\angle ABC = 24^\circ$, verifying that the triangle is isosceles.
In conclusion, the given diagram implies that the triangle $ABC$ is an isosceles triangle with angles of $24^\circ$. This can be verified by computing the length of the hypotenuse and using the Pythagorean Theorem.
To know more about equation click-
http://brainly.com/question/2972832
#SPJ1
Answer:
78
Step-by-step explanation:
Sarah has been an exemplary employee! The library has given her a 5% raise in recognition of
her hard work. If Sarah normally has a net salary of $212.50, what will Jessica’s net salary be now?
Remember, you calculated that 15% of Sarahs gross salary is withheld each week.
Answers
The correct value of Jessica's new net salary will be $225.
To calculate Jessica's new net salary after a 5% raise, we need to first determine Sarah's gross salary. We know that Sarah's net salary is $212.50, and 15% of her gross salary is withheld each week.
Let's denote Sarah's gross salary as "G." We can set up the following equation:
G - 15% of G = $212.50
Simplifying the equation, we have:
G - 0.15G = $212.50
0.85G = $212.50
G = $212.50 / 0.85
G ≈ $250
Sarah's gross salary is approximately $250.
Now, to find Jessica's new net salary after a 5% raise, we can calculate 5% of Sarah's gross salary and subtract the withheld amount:
Jessica's net salary = Sarah's gross salary + 5% of Sarah's gross salary - 15% of Sarah's gross salary
Jessica's net salary = $250 + 0.05 * $250 - 0.15 * $250
Jessica's net salary = $250 + $12.50 - $37.50
Jessica's net salary = $225
Therefore, Jessica's new net salary will be $225.
Learn more about equation here:
https://brainly.com/question/29174899
#SPJ8
R(-6, 1), S(-3, -3)
Find the coordinates of the midpoint of a segment with given endpoints
Answers
Answer:
\(\boxed {\boxed {\sf ( - \frac{9}{2}, -1) \ or \ (-4.5, -1) }}\)
Step-by-step explanation:
We are asked to find the midpoint of a line segment. When you find the midpoint, you essentially find the average of the x-coordinates and the y-coordinates. The midpoint formula is:
\((\frac {x_2+x_1)}{2}, \frac{y_2+y_1}{2})\)
In this formula, (x₁, y₁) and (x₂, y₂) are the endpoints of the line segment. we are given the endpoints R (-6, 1) and S (-3, -3). If we match the value and the corresponding variable we see that:
x₁= -6 y₁= 1 x₂= -3 y₂= -3Substitute the values into the formula.
\(( \frac{-3 + -6}{2} , \frac{ 1+ -3}{2} )\)
Solve the numerators.
-3 + -6 = -9 1 + -3 = -2\((\frac {-9}{2}, \frac {-2}{2})\)
Divide.
\(( - \frac {9}{2}, -1})\)
The fraction can also be written as a decimal.
\((-4.5 , -1)\)
The midpoint of the line segment RS is (-9/2, -1) or (-4.5, -1).
If f(x) = sin(ln(2x)), then f’(x)=

Answers
Answer:
B. cos(ln(2x))/x
Step-by-step explanation:
We know that the inverse of sin is cosine. Note, arcsin means the same thing as inverse sin:
sin(ln(2x))Because sin (a) = sin (b) --> a = arcsin (b)
Therefore: ln(2x) = arcsin(y)Solve ln(2x)=arcsin(y) for x(e^arcsin(y))/2Subsitute y = x
(e^arcsin(x))/2Therefore, we get the answer as cos(ln(2x))/xIf a Play Station was bought for $558 after a 10%
discount, what was the original price of the Play
Station?
Answers
The original price of the play station is $620.
Given that, the cost of the play station=$558 and discount=10%.
We need to find the original price of the play station.
What is a discount?The definition of discount is reduced prices or something being sold at a price lower than that item is normally sold for.
Let the original price be x.
Now, x-10% of x=558
⇒x-0.1x=558
⇒0.9x=558
⇒x=$620
Therefore, the original price of the play station is $620.
To learn more about the discount visit:
https://brainly.com/question/3541148.
#SPJ2
2. Write the absolute value of the following. a) | -6 -3 | . b) | 0 - 12 |.
Answers
Answer:
a)9. b) 12
Step-by-step explanation:
a) | -6 -3 | .
-6-3 = -9
|-9| =9
b) | 0 - 12 |.
0-12=-12
|-12|=12
In each of the following graphs, find the lengths of the line segments shown. Write your answers (in simplest
radical form if they are not integers.
(a)
B
(b)
Q

Answers
The length of the two segments, written as radicals, are:
AB = √117
PQ = √244
How to find the length of the segments shown?Remember that for a segment whose endpoints are (x₁, y₁) and (x₂, y₂), the length of the segment is:
L = √( (x₂ - x₁)² + (y₂ - y₁)²)
First, for the segment AB the endpoints are:
A = (-4, -4)
B = (2, 5)
Then the length is:
L = √( (-4 - 2)² + (-4 - 5)²)
L = √117
For the segment PQ the endpoints are:
P = (-6, 8)
Q = (6, -2)
The length is:
L = √( (-6 - 6)² + (8 + 2)²)
L = √244
Learn more about segments at:
https://brainly.com/question/17374569
#SPJ1
The National Cancer Institute estimates that 3.65% of women in their 60s get breast cancer. A mammogram can typically identify correctly 85% of cancer cases and 95% of cases without cancer. What is the probability that a woman in her 60s who has a positive test actually has breast cancer?
Answers
Answer:
39.17% probability that a woman in her 60s who has a positive test actually has breast cancer
Step-by-step explanation:
Bayes Theorem:
Two events, A and B.
\(P(B|A) = \frac{P(B)*P(A|B)}{P(A)}\)
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.
In this question:
Event A: Positive test.
Event B: Having breast cancer.
3.65% of women in their 60s get breast cancer
This means that \(P(B) = 0.0365\)
A mammogram can typically identify correctly 85% of cancer cases
This means that \(P(A|B) = 0.85\)
Probability of a positive test.
85% of 3.65% and 100-95 = 5% of 100-3.65 = 96.35%. So
\(P(A) = 0.85*0.0365 + 0.05*0.9635 = 0.0792\)
What is the probability that a woman in her 60s who has a positive test actually has breast cancer?
\(P(B|A) = \frac{0.0365*0.85}{0.0792} = 0.3917\)
39.17% probability that a woman in her 60s who has a positive test actually has breast cancer
Workout AG in the cuboid below. (3d trig)

Answers
The length of the diagonal AG = 7.56 cm.
Finding diagonal of cuboid:A cuboid is a three-dimensional shape that is bounded by six rectangular faces. It is also known as a rectangular prism. A cuboid has six faces, twelve edges, and eight vertices.
To find the Length of the side AG, find the length of AC by using the Pythagorean formula. Now using the trigonometric ratios formulas find the length of AG.
Here we have a cuboid
Where
AD = 23 cm
DC = 18 cm
∠GAC = 75°
From the right angle triangle, ADC
=> AC² = AD² + DC² [ Using the Pythagorean formula ]
=> AC² = (23)² + (18)²
=> AC² = 529 + 324
=> AC = √853 = 29.20
From the right angle triangle, AGC
=> Cos B = AC/AG
=> Cos 75° = 29.20/AG
=> AG = Cos 75° (29.20)
=> AG = (0.26)(29.20)
=> AG = 7.56
Therefore
The length of the diagonal AG = 7.56 cm.
Learn more about Cuboid at
https://brainly.com/question/29446615
#SPJ1
What's the area of the shape?
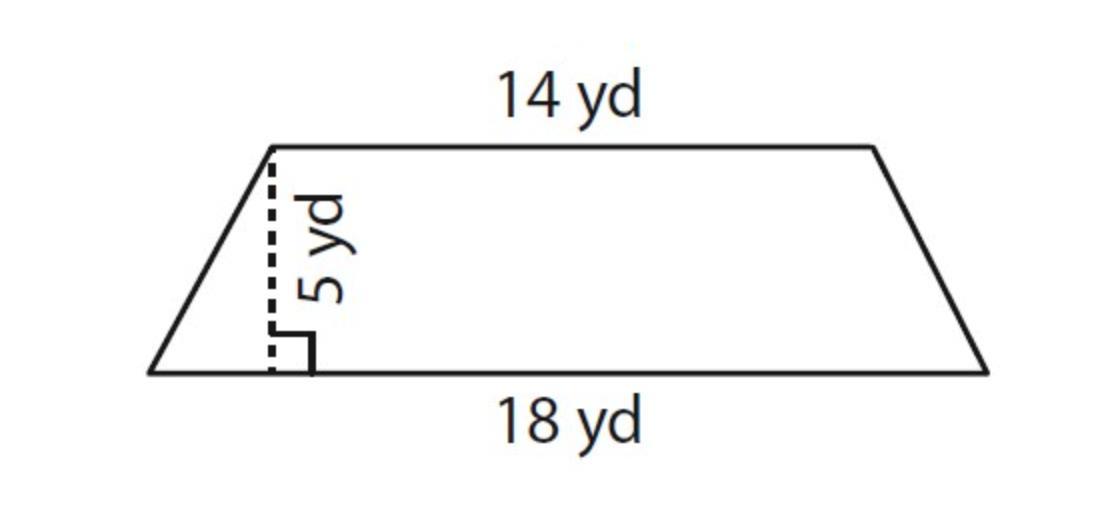
Answers
Answer:
Area = 80 yd²
Step-by-step explanation:
=> First make a common base:
Common base = (Base 1 + Base 2) / 2
Common base = (14 + 18) / 2
Common base = 32 / 2
Common base = 16
=> Now multiply the common base by the height to find the area:
Area of the figure = Common Base * Height of the figure
A = 16 * 5
A = 80
Hope this helps!
The total number of people that went to the out of town tournament was 42. How many players in chaperones went on the trip?
Answers
Answer:7 jogadore participaram do jogo
solve the following inequality for z. write your answer in simplest form. -9-(2z-7)>-2z-6-5z
Answers
Answer:
z > -4/5
Step-by-step explanation:
-9 - (2z - 7) > -2z - 6 - 5z
Get rid of the parenthesis
*There is the number one in front of the parenthesis.-9 - 2z + 7 > -2z - 6 - 5z
Combine like terms:
-2 - 2z > -7z - 6
+2 > +2
Add 2 to both sides.
-2z > -7z - 4
+7z > +7z
Add 7 to both sides.
5z > -4
Divide both sides by 5 to get z.
z > -4/5
The sign stays the same unless you divide by a negative number---------------------------------
More on inequalities: https://brainly.com/question/21857626
Hope this helps! :)
Trình bày
So sánh 4 và √37-2
Answers
the answer is 393
trust me
Gift are packaged in cylinders
each cylinder is 12cm high with diameter of 8cm
calculate the volume of each cylinder
use 3 as a value for J
Answers
Answer:
V = 192π cm³ ≈ 603 cm³
Step-by-step explanation:
V = πR²h
V = π(8/2)²(12)
V = 192π cm³ ≈ 603 cm³
J = 3 Hooray, but why?
Answer:
Step-by-step explanation:
Radius r = 4 cm
Height h = 12 cm
Volume = πr²h = 192π cm³ ≈ 576 cm³
NO LINKS!! Please help me

Answers
Answer:
A
Step-by-step explanation:
Since cosine is positive and sine is negative that puts θ in Quad IV.
From right triangles we know:
Cos θ = adjacent/hypotenuse = 5/13
sin θ = opposite/hypotenuse = ?/13
To find the opposite side across from θ use the pythagorean theorem.
5² + y² = 13²
25 + y² = 169
y² = 144
y = 12
we are given that sin is < 0 so sinθ = -12/13
Answer:
A
Step-by-step explanation:
\(\cos(\theta)=\dfrac{\textsf{adjacent side}}{\textsf{hypotenuse}}=\dfrac{5}{13}\)
\(\textsf{As }\cos(\theta) > 0 \textsf{ the angle is in quadrant I or IV}\)
Using Pythagoras' Theorem a² + b² = c² to find the side opposite the angle:
⇒ 5² + b² = 13²
⇒ b² = 144
⇒ b = 12
⇒ opposite side = 12
\(\implies \sin(\theta)=\dfrac{\textsf{opposite side}}{\textsf{hypotenuse}}=\dfrac{12}{13}\)
\(\textsf{As }\sin(\theta) < 0 \textsf{ then }\sin(\theta)=-\dfrac{12}{13} \textsf{ and the angle is in either quadrant III or quadrant IV}\)
Therefore, the common quadrant is quadrant IV and
\(\sin(\theta)=-\dfrac{12}{13}\)
The perimeter of a triangle is 100cm and the angles are in the ratio: 1:3:5 find the length of each side triangle
Answers
By applying the rule of sin, it can be concluded that the length of the sides of the triangle is 15.48 cm, 39.68 cm, and 44.84 cm.
Triangle is a 2D shape that is bounded by three sides and has three vertices. The perimeter of a triangle is the sum of the lengths of the three sides of the triangle.
Perimeter = a + b + c, where a, b, and c are the sides of the triangle
One of the most important properties of a triangle is that the sum of the angles in a triangle equals 180°.
The rule of sin describes the ratio of the angles corresponding to the side lengths of the sine function.
a / sin A = b / sin B = c / sin C, where A, B, and C are the angles of the triangle
If the ratio of the angles is 1 : 3 : 5 and let x be the smallest angle, then we can put this information into the following equation:
Total angle = A + B + C
180° = x + 3x + 5x
180° = 9x
x = 20°
Then we can calculate the other angles:
A = 20°
B = 3x = 3 * 20° = 60°
C = 5x = 5 * 20° = 100°
Now we put the value of A, B, and C into the rule of sin equation:
a / sin A = b / sin B
a / sin 20° = b / sin 60°
a / 0.34 = b / 0.87
a = 0.34 * b / 0.87
a = 0.39b
c / sin C = b / sin B
c / sin 100° = b / sin 60°
c / 0.98 = b / 0.87
c = 0.98 * b / 0.87
c = 1.13b
Then we go back to the perimeter formula:
perimeter = a + b + c
100 = 0.39b + b + 1.13b
100 = 2.52b
b = 39.68 cm
Then we can calculate the length of the other sides, a and c:
a = 0.39b
= 0.39 * 39.68
= 15.48 cm
c = 1.13b
= 1.13 * 39.68
= 44.84 cm
Thus, the length of the sides of the triangle is 15.48 cm, 39.68 cm, and 44.84 cm.
To learn more about the rule of sin, click here: https://brainly.com/question/27174058
#SPJ4

A Collection of books consist of six maths
books and four English books A Book is
Collected at random from the collection,
find the probability of choosing
A math Book,
An english books,
Either a maths or an English Book
Answers
Probability of choosing a math book is 3/5
Probability of choosing an English book is 2/5
Probability of choosing either a math or an English book is 1.
To find the probabilities, we need to determine the total number of possible outcomes and the number of favorable outcomes for each scenario.
Probability of choosing a math book:
Out of the total collection of 6 math books and 4 English books, the number of math books is 6. The total number of books in the collection is 10. Therefore, the probability of choosing a math book is given by:
Probability of choosing a math book = Number of math books / Total number of books
= 6 / 10
= 3/5
Probability of choosing an English book:
Out of the total collection of 6 math books and 4 English books, the number of English books is 4. The total number of books in the collection is still 10. Therefore, the probability of choosing an English book is given by:
Probability of choosing an English book = Number of English books / Total number of books
= 4 / 10
= 2/5
Probability of choosing either a math or an English book:
To find this probability, we add the probabilities of choosing a math book and choosing an English book since these two events are mutually exclusive (a book cannot be both a math book and an English book). Therefore:
Probability of choosing either a math or an English book = Probability of choosing a math book + Probability of choosing an English book
= 3/5 + 2/5
= 5/5
= 1
For more such questions on Probability visit:
https://brainly.com/question/251701
#SPJ8
May I please have your help?

Answers
Answer:
A
Step-by-step explanation:
please say thank you and rate 5 stars and verify
Which of these numbers are greater than 24? Check all that apply.
O A. 12
B. 15
O C. 42
D. 41
E. 13
D F. 18
Answers
Answer:
A, B, E, F
Step-by-step explanation:
24>12, 24>15, 24>13, 24>18, 24<42, 24<41
In order to set the price of a smoothie on his menu, Andre adds 225% increase onto the cost of the ingredients, which is $1.50. Find the price of the smoothie.
HELP THIS IS DUE TOMORROW!
Answers
Please help 10points!
Find x.

Answers
Answer:
The value of x is 19.
Step-by-step explanation:
Given:
m∠1 = (4x + 9)°
m∠2 = (x - 14)°
Since m∠1 and m∠2 are complementary angles, we have:
m∠1 + m∠2 = 90°
Substituting the given expressions for m∠1 and m∠2:
(4x + 9)° + (x - 14)° = 90°
Combining like terms:
4x + 9 + x - 14 = 90
Combining the x terms and the constant terms:
5x - 5 = 90
Adding 5 to both sides:
5x = 90 + 5
Simplifying:
5x = 95
Dividing both sides by 5:
x = 95 / 5
Simplifying further:
x = 19
PLEASE HELP! i have by the end of the day to turn this in. PLEASE DONT GUESS

Answers
Answer: See step by step
Step-by-step explanation: Angle 2 and 3 are vertical angles since they both share a vertex and has cross intersecting lines. Angle 6 and 7 are supplementary angles because they forma linear pair.
Answer:
I have multiple answers for this.
Verticle Angles: 2 &4, 3&1, 6&8, 7&5
Supplementary Angles: 2&1, 2&3, 3&4, 1&4, 6&7, 7&8, 6&5, 5&8
Step-by-step explanation:
Verticle angles are aross from one another, not next to each other, while the Supplementary angles ARE next to each other and not across from one another. I hope this helps you :)
Consider a line whose slope is 6 and which passes through the point (8.–2).
3. Write the equation of the
4. Write the equation of the
line in point-slope form.
line in slope-intercept form.
Answers
Answer:
\(y=6(x-8)-2\qquad\text{point-slope form}\)
\(y=6x-50\qquad\text{slope-intercept form}\)
Step-by-step explanation:
The equation of a line can be written in several forms. Two of the most-used forms are the point-slope and the slope-intercept forms.
The point-slope form requires to have one point (xo, yo) through which the line passes and the slope m. The equation expressed in this form is:
\(y=m(x-xo)+yo\)
The slope-intercept form requires to have the slope m and the y-intercept b, or the y-coordinate of the point where the line crosses the y-axis. The equation is:
\(y=mx+b\)
The line considered in the question has a slope m=6 and passes through the point (8,-2). These data is enough to find the point-slope form of the line:
\(\boxed{y=6(x-8)-2\qquad\text{point-slope form}}\)
To find the slope-intercept form, we operate the above equation:
\(y=6x-48-2\)
\(\boxed{y=6x-50\qquad\text{slope-intercept form}}\)