maria had $150 in gift certificates to use in a record store.she bought fewer than 20 recordings.each tape cost $5.95 and each cd cost $8.95. how many of each type of recordings might she have bought(it has to be graphed so i need points to plot)
Answers
Answer:
keep the canon digital marketing. this was not able the first one. it has to go on, I will not
Related Questions
Solve for x in the diagram below.
60°
(x +45)

Answers
Answer: 15
Step-by-step explanation:
Ari and Greg share a 12-ounce bucket of clay. By the end of the week, Ari has used 1 6 of the bucket, and Greg has used 2 3 of the bucket of clay. How many ounces are left in the bucket?
Answers
Answer:
2 ounces of clay is left in the bucket
Step-by-step explanation:
Total amount of clay in the bucket = 12 ounce
Ari used 1/6th of the clay in the bucket and Greg used 2/3 of the clay in the bucket
Hence, the remaining clay in the bucket
12 - 1/6 *12 - 2/3 * 12
12 - 2-8
2
Find f(a),f(a+h), and the difference quotient f(a+h)−f(a) /h, where h is not equal to 0. f(x)=9x2+7
Answers
The value of f(a) is \(9a^2 + 7\). The value of f(a+h) is \(9(a+h)^2 + 7\). The difference quotient (f(a+h) - f(a))/h simplifies to 18a + 9h for the function \(f(x) = 9x^2 + 7.\)
Let's break down the calculations step by step. First, to find f(a), we substitute a into the function: \(f(a) = 9(a^2) + 7 = 9a^2 + 7\).
Next, to find f(a+h), we substitute (a+h) into the function: \(f(a+h) = 9(a+h)^2 + 7\). Expanding the square, we get \(f(a+h) = 9(a^2 + 2ah + h^2) + 7 = 9a^2 + 18ah + 9h^2 + 7\).
Lastly, to calculate the difference quotient, we subtract f(a) from f(a+h) and divide by h: \((f(a+h) - f(a))/h = [(9a^2 + 18ah + 9h^2 + 7) - (9a^2 + 7)]/h = (18ah + 9h^2)/h.\)
Simplifying further, we can cancel out h from the numerator, giving us the final result: 18a + 9h.
Therefore, the difference quotient (f(a+h) - f(a))/h simplifies to 18a + 9h for the function \(f(x) = 9x^2 + 7.\)
Learn more about quotient here: https://brainly.com/question/27796160
#SPJ11
plssss help me this is due tomorrow morning

Answers
Find percent -> 2nd month.
4264*.25==1066 phone calls+=4264
==5330 for 2nd month.
for 2nd -> 3rd
6396==5330*x, solve algebraically to get .20 == 20% increase from 2nd month to 3rd month.
given the least squares regression line y^= -2.88 + 1.77x, and a coefficient of determination of 0.81, the coefficient of correlation is:
a) -0.88
b)+0.88
c) +0.90
d)-0.90
Answers
The coefficient of correlation can be determined using the coefficient of determination, which is given as the square of the correlation coefficient. In this case, the coefficient of determination is 0.81, indicating that 81% of the variability in the dependent variable (y) can be explained by the independent variable (x).
To find the coefficient of correlation, we take the square root of the coefficient of determination. Taking the square root of 0.81 gives us 0.9. However, the coefficient of correlation can be positive or negative, depending on the direction of the relationship between the variables.
Looking at the given regression line y^= -2.88 + 1.77x, the positive slope of 1.77 indicates a positive relationship between x and y. Therefore, the coefficient of correlation would also be positive.
Hence, the answer is (c) +0.90, indicating a positive correlation between the variables.
Learn more about square root here: https://brainly.com/question/29286039
#SPJ11
Graph the following function on the axes provided.
(4x + 17
-2
f(x) =
for x < -3
for
x>0
Answers
The graph of the function is added as an attachment
How to determine the graph of the equationFrom the question, we have the following parameters that can be used in our computation:
f(x) = 4x + 17
f(x) = -2
Also, we have the interval to be
f(x) = 4x + 17 for x <-3
f(x) = -2 for x > 0
The above expression is a piecewise function
Next, we plot the graph and the intervals
See attachment for the graph of the equations
Read more about graphs at
https://brainly.com/question/30422919
#SPJ1

margo draws a triangle. The lengths of the sides of he triangle are 8 inches, 15 inches, and 17 inches. Margo uses the area of three squares to show that the triangle is a right triangle. Which of these could be the area, in square units, of a square that margo uses.
Answers
Answer:
Either of the following square values:
\(8^{2} =64 \,\,in^2\\15^2= 225\,\,in^2\\17^2=280\,\,in^2\)
Step-by-step explanation:
The three possible answers correspond to the square of the sides of the triangles via the Pythagorean theorem. And these are:
\(8^{2} =64 \,\,in^2\\15^2= 225\,\,in^2\\17^2=280\,\,in^2\)
5. Write an equation in point-slope form for the line through the given point with the given slope.
(10,-9); m -2
ay-10-2(x+9)
b. y-9--2(x + 10)
c. y-9-2(x - 10)
y+9-2(x 10)
d.
Answers
Answer:
y + 9 = -2(x - 10)
The correct answer is d.
assume that T is a linear transformation. Find the standard matrix of T. 1. T:R? → R4,7(ei) = (3,1,3,1) and T (ez) = (-5,2,0,0), where ej = (1,0) and e2 = (0,1). 2. T:R3 → R2, T(ei) = (1,3), T(C2) = (4, -7), and T(ez) = (-5,4), where ej, ez, ez are the columns of the 3 x 3 identity matrix. ro: 3. T:R2 + R2 rotates points (about the origin) through 31/2 radians (counterclockwise). 4. T:R2 → R2 rotates points (about the origin) through --1/4 radians (clockwise). [Hint: T(ei) = (1/12, -1/72).] 5. T:R2 + R2 is a vertical shear transformation that maps e, into e, - 2e, but leaves the vector ez unchanged. 6. T:R2 + R2 is a horizontal shear transformation that leaves e, unchanged and maps e2 into e2 + 3ej.
Answers
The standard matrix of a linear transformation T can be found by using the formula A = [T(e1) T(e2) ... T(en)], where A is the standard matrix, e1, e2, ..., en are the columns of the identity matrix, and T(e1), T(e2), ..., T(en) are the images of the identity matrix columns under the transformation T.
1. For the first transformation, the standard matrix of T can be found by using the formula A = [T(e1) T(e2)] = [(3,1,3,1) (-5,2,0,0)] = [[3 -5] [1 2] [3 0] [1 0]]. Therefore, the standard matrix of T is [[3 -5] [1 2] [3 0] [1 0]].
2. For the second transformation, the standard matrix of T can be found by using the formula A = [T(e1) T(e2) T(e3)] = [(1,3) (4,-7) (-5,4)] = [[1 4 -5] [3 -7 4]]. Therefore, the standard matrix of T is [[1 4 -5] [3 -7 4]].
3. For the third transformation, the standard matrix of T can be found by using the formula A = [T(e1) T(e2)] = [cos(31/2) -sin(31/2) sin(31/2) cos(31/2)], where cos(31/2) and sin(31/2) are the cosine and sine of 31/2 radians, respectively. Therefore, the standard matrix of T is [cos(31/2) -sin(31/2) sin(31/2) cos(31/2)].
4. For the fourth transformation, the standard matrix of T can be found by using the formula A = [T(e1) T(e2)] = [cos(-1/4) -sin(-1/4) sin(-1/4) cos(-1/4)], where cos(-1/4) and sin(-1/4) are the cosine and sine of -1/4 radians, respectively. Therefore, the standard matrix of T is [cos(-1/4) -sin(-1/4) sin(-1/4) cos(-1/4)].
5. For the fifth transformation, the standard matrix of T can be found by using the formula A = [T(e1) T(e2)] = [(1,0) (2,1)] = [[1 2] [0 1]]. Therefore, the standard matrix of T is [[1 2] [0 1]].
6. For the sixth transformation, the standard matrix of T can be found by using the formula A = [T(e1) T(e2)] = [(1,0) (3,1)] = [[1 3] [0 1]]. Therefore, the standard matrix of T is [[1 3] [0 1]].
Learn more about Matrix
brainly.com/question/28180105
#SPJ11
Use symmetry to evaluate the following integral. 8 S (3+x+x? +x°) dx •*• -8 8 S (3+x+x+ +xº) dx = ) (Type an integer or a simplified fraction) x a . -8
Answers
We can take advantage of the integrand's symmetry over the y-axis to employ symmetry to evaluate the integral [-8, 8] (3 + x + x2 + x3) d.
As a result, the integral across the range [-8, 8] can be divided into two equally sized pieces, [-8, 0] and [0, 8].
Taking into account the integral throughout the range [-8, 0]: [-8, 0] (3 + x + x² + x³) dx
The integral of an odd function over a symmetric interval is zero because the integrand is an odd function (contains only odd powers of x). The integral over [-8, 0] hence evaluates to zero.
learn more about advantage here :
https://brainly.com/question/23428799
#SPJ11
The spray from a spinning lawn sprinkler covers a circle. The distance around the circle is of 64pi feet. What is the radius of the circle covered by the lawn sprinkler?
Answers
To find the radius of the circle covered by the lawn sprinkler, we can use the formula for the circumference of a circle: C = 2πr, where C is the circumference and r is the radius.
Given that the distance around the circle is 64π feet, we can equate this to the circumference of the circle: 64π = 2πr.
By canceling out the π terms on both sides of the equation, we get
64 = 2r.
Dividing both sides of the equation by 2, we find that the radius of the circle is r = 32 feet.
Therefore, the radius of the circle covered by the lawn sprinkler is 32 feet.
To learn more about circumference of a circle visit:
brainly.com/question/27177006
#SPJ11
can someone help me with this please

Answers
Answer:
Step-by-step explanation:
Answer is 30
4a - 3 =
2a + 7
I need help
Answers
Answer:
a=5
Step-by-step explanation:
4a−3−2a=2a+7−2a
2a−3=7
2a−3+3=7+3
2a=10
2a /2 = 10 /2
a=5
Find FH
A. 13.5
B. 6.0
C. 8.1
D. 6.7

Answers
Step-by-step explanation:
the FH seems to be option b.6.0
........

can someone help me on this?

Answers
Answer:
#4 should be C
You can use substitution to solve this system.
since y = x, you can plug in that in the place of x
New equation: x + x = 4
x = 2
Now plug in x for the original equation
y = 2
so the answer is 2,2
:)
Alberto started out bench pressing 60 pounds. He then added 5 pounds every week. Determine whether the situation is linear or nonlinear, and proportional or nonproportional
Answers
Answer
linear
nonproportional
Step-by-step explanation:
Since for each equal change in time (1 week), there is an equal change in weight (5 lb), the situation is linear.
At time zero, the first week, the weight was not zero. It was 60 lb, so it is not proportional.
Answer:
linear
nonproportional
help.me with Ap calc please

Answers
Answer:
\(\displaystyle f'(1) = 6\)
General Formulas and Concepts:
Calculus
Differentiation
DerivativesDerivative NotationDerivative Property [Multiplied Constant]: \(\displaystyle \frac{d}{dx} [cf(x)] = c \cdot f'(x)\)
Derivative Property [Addition/Subtraction]: \(\displaystyle \frac{d}{dx}[f(x) + g(x)] = \frac{d}{dx}[f(x)] + \frac{d}{dx}[g(x)]\)
Basic Power Rule:
f(x) = cxⁿf’(x) = c·nxⁿ⁻¹Step-by-step explanation:
Step 1: Define
Identify
\(\displaystyle f(x) = 5x - 1 + \ln x\)
Step 2: Differentiate
[Function] Derivative Property [Addition/Subtraction]: \(\displaystyle f'(x) = \frac{d}{dx}[5x] - \frac{d}{dx}[1] + \frac{d}{dx}[\ln x]\)Rewrite [Derivative Property - Multiplied Constant]: \(\displaystyle f'(x) = 5 \frac{d}{dx}[x] - \frac{d}{dx}[1] + \frac{d}{dx}[\ln x]\)Derivative Rule [Basic Power Rule]: \(\displaystyle f'(x) = 5 - 0 + \frac{d}{dx}[\ln x]\)Logarithmic Differentiation: \(\displaystyle f'(x) = 5 + \frac{1}{x}\)Substitute in x: \(\displaystyle f'(1) = 5 + \frac{1}{1}\)Simplify: \(\displaystyle f'(1) = 6\)Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation
Given the value of cosine,
Cos 0=1/5
Find the value of sine
Sin(0)=

Answers
Answer:
25896
Step-by-step explanation:
A rectangular field is ten times as long as it is wide. If the perimeter of the field is 1430 feet, find the length and width of the field?
Answers
Answer:
below
Step-by-step explanation:
The steps to solve this are:
The perimeter of a rectangle is given by p=2(l+w) where p is the perimeter, l is the length and w is the width. We are told the length of the field is 10 times the width so l=10w. Using this in the formula above we get:
2090=2(10w+w)
22w=2090
w=95 ft
l=950 ft
FILL IN THE BLANK a(n) ____ consists of a rectangle divided into three sections.
Answers
Answer:
Step-by-step explanation:4
The equations represent the elevations, y, of two hikers, in meters, after x hour. Wich ordered pair, (0, 0), (1, 7) or (2, 10), is a solution to the system? will the hikers ever be the same elevation? explain. Y = 6x + 1
y = 3x + 4
Answers
yes. the hikers will ever be the same elevation.6+1=7 the same elevation.
Y = 6x + 1
FIll the value of y in this equation
3x + 4= 6x + 1
3x=4-1
x=3/3=1
Y = 6x + 1
FIll the value of x in this equation
6+1=7. The height above or below a specified reference point, most frequently a reference geoid, which is a mathematical representation of the Earth's sea level as an equipotential gravitational surface, determines a location's elevation. In most cases, elevation is used to describe locations on the surface of the Earth, whereas altitude or geopotential height is used to describe locations above the surface, such as those of flying airplanes or orbiting satellites, and depth is used to describe locations below the surface. Elevation should not be confused with the angular separation from the Earth's center. The summits of Mount Everest and Chimborazo have the highest elevation and greatest geocentric distance, respectively, because of the equatorial bulge.
Learn more about elevation from
brainly.com/question/25748640
#SPJ4
what is the value of x and y
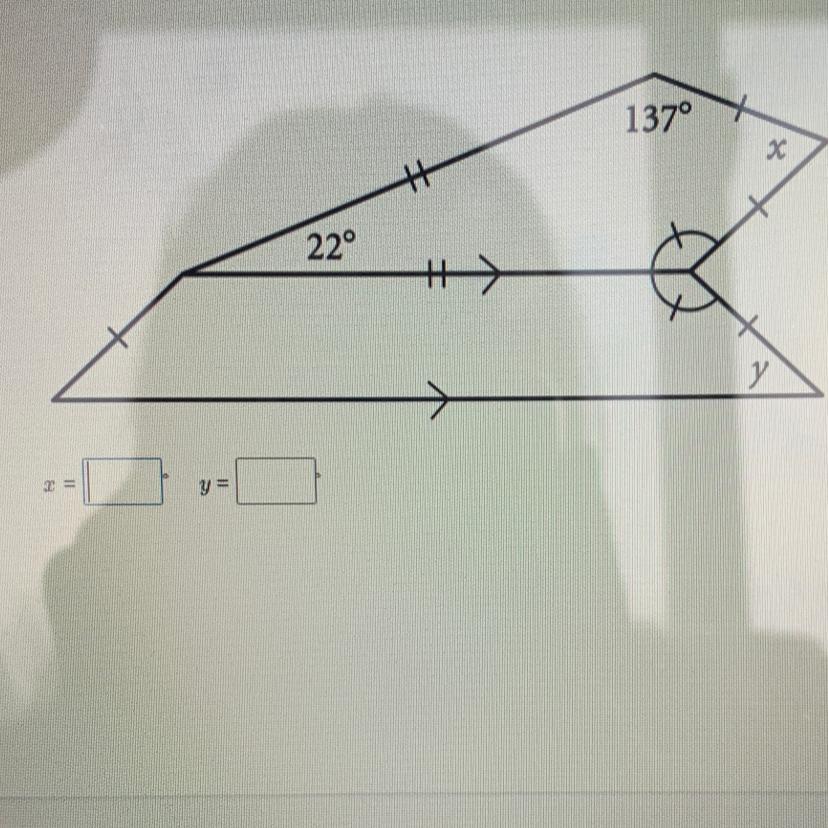
Answers
Answer: x=64 y=43
Step-by-step explanation:
Explanation
find the surface area. help i’m confused

Answers
The radius of a circle is 2 meters. What is the area of a sector bounded by a 135 degree arc? Give the exact answer in simplest form
Answers
Answer:
Area of circle bounded by a 135 ° arc is 4.71 m ²
Step-by-step explanation:
Given that :-Radius of circle, r = 2 m
Angle of the circle , θ = 135 °
To Find :-Area of circle bounded by a 135 ° arc.
Solution :-Using Formula
Area of circle = θ/ 360 × π × r ²
substitute the values,
Area of circle = 135 /360 × 3.14 × ( 2 m) ²
solve it
Area = 27 / 72 × 3.14 × 4 m ²
Area = 27 / 18 × 3.14
Area = 1.5 × 3.14
Area = 4.71 m ²
Therefore, Area of circle bounded by a 135 ° arc is 4.71 m ²
Answer:
it's 3/2pi
Step-by-step explanation:
.
PLEASE HELP NOW
Rewrite the equation in Ax+By=C form.
Use integers for A, B, and C.
y+6=5(x-3)
2

Answers
Answer:
answer is 21= 5x- y
Step-by-step explanation:
y+6=5(x-3)
y+6=5x-15
y = 5x-15-6
y = 5x-21
rearrange this equation as formAx+By=C
5X - y = 21
Find the Product of (s^2+5s)(s^3+4s^2).
Answers
The result of the product \((s^2+5s)(s^3+4s^2)\) is \(s^5+9s^4+20s^3\)
The product is given as:
\((s^2+5s)(s^3+4s^2)\)
Rewrite as:
\((s^2+5s)(s^3+4s^2) = (s^2+5s) \times (s^3+4s^2)\)
Expand the expression on the right-hand side
\((s^2+5s)(s^3+4s^2) = s^2\times (s^3+4s^2)+5s \times (s^3+4s^2)\)
Distribute the expressions
\((s^2+5s)(s^3+4s^2) = s^5+4s^4+5s^4+20s^3\)
Evaluate like terms
\((s^2+5s)(s^3+4s^2) = s^5+9s^4+20s^3\)
Hence, the result of the product \((s^2+5s)(s^3+4s^2)\) is \(s^5+9s^4+20s^3\)
Read more about products at:
https://brainly.com/question/24963015
rotation 90 clockwise about the origin B (- 2,) , C(-4,3), Z(-3,4), X (- 1,4)

Answers
The coordinates of the images of the points are B'(x, y) = (0, 2), C'(x, y) = (3, 4), Z'(x, y) = (4, 3) and X'(x, y) = (4, 1), respectively.
How to rotate points about the origin
In this problem we find four points set on Cartesian plane, each of which has to be transformed by using the following transformation rule about the origin:
(x', y') = (x · cos θ - y · sin θ, x · sin θ + y · cos θ)
Where:
(x, y) - Coordinates of the original point.
θ - Angle of rotation, in degrees.
If we know that B(x, y) = (- 2, 0), C(x, y) = (- 4, 3), Z(x, y) = (- 3, 4), X(x, y) = (- 1, 4) and θ = 90°, then the coordinates of the resulting point:
B'(x, y) = (- 2 · cos (- 90)° - 0 · sin (- 90°), - 2 · sin (- 90°) + 0 · cos (- 90°))
B'(x, y) = (0, 2)
C'(x, y) = (- 4 · cos (- 90°) - 3 · sin (- 90°), - 4 · sin (- 90°) + 3 · cos (- 90°))
C'(x, y) = (3, 4)
Z'(x, y) = (- 3 · cos (- 90°) - 4 · sin (- 90°), - 3 · sin (- 90°) + 4 · cos (- 90°))
Z'(x, y) = (4, 3)
X'(x, y) = (- 1 · cos (- 90°) - 4 · sin (- 90°), - 1 · sin (- 90°) + 4 · cos (- 90°))
X'(x, y) = (4, 1)
Finally, we proceed to graph the locations of the points, both original and resulting, by means of a graphing tool.
To learn more on rotations: https://brainly.com/question/1571997
#SPJ1

Suppose the real 2 × 2 matrix M has complex eigenvalues a ± bi, b 6= 0, and the real vectors u and v form the complex eigenvector u + iv for M with eigenvalue a − bi (note the difference in signs). The purpose of this exercise is to show that M is equivalent to the standard rotation–dilation matrix Ca,b.
a. Show that the following real matrix equations are true: Mu = au+bv, Mv = −bu+av.
b. Let G be the matrix whose columns are u and v, in that order. Show that MG = GCa,b.
c. Show that the real vectors u and v are linearly independent in R2. Suggestion: first show u ≠ 0, v ≠ 0. Then suppose there are real numbers r, s for which ru+sv = 0. Show that 0 = M(ru+sv) implies that −su+rv = 0, and hence that r = s = 0.
d. Conclude that G is invertible and G−1MG = Ca,b
Answers
a. Im(Mu) = Im(Mu + iMv)
=> 0 = bv - aiv
=> Mv = -bu + av
b. G^-1MG is equivalent to the standard rotation-dilation matrix Ca,b.
a. We have the complex eigenvector u + iv with eigenvalue a - bi. By applying the matrix M to this eigenvector, we get:
Mu = M(u + iv) = Mu + iMv
Since M is a real matrix, the real and imaginary parts must be equal:
Re(Mu) = Re(Mu + iMv)
=> Mu = au + biv
Similarly,
Im(Mu) = Im(Mu + iMv)
=> 0 = bv - aiv
=> Mv = -bu + av
b. Let's consider the matrix G = [u | v], where the columns are u and v in that order. Multiplying this matrix by M, we have:
MG = [Mu | Mv] = [au + bv | -bu + av]
On the other hand, let's compute GCa,b:
GCa,b = [u | v] Ca,b = [au - bv | bu + av]
Comparing these two expressions, we can see that MG = GCa,b.
c. To show that u and v are linearly independent, we assume that there exist real numbers r and s such that ru + sv = 0. Applying the matrix M to this equation, we get:
0 = M(ru + sv) = rMu + sMv
0 = r(au + bv) + s(-bu + av)
0 = (ar - bs)u + (br + as)v
Since u and v are complex eigenvectors with distinct eigenvalues, they cannot be proportional. Therefore, we have ar - bs = 0 and br + as = 0. Solving these equations simultaneously, we find that r = s = 0, which implies that u and v are linearly independent.
d. Since u and v are linearly independent, the matrix G = [u | v] is invertible. Let's denote its inverse as G^-1. Now, we can show that G^-1MG = Ca,b:
G^-1MG = G^-1 [au + bv | -bu + av]
= [G^-1(au + bv) | G^-1(-bu + av)]
= [(aG^-1)u + (bG^-1)v | (-bG^-1)u + (aG^-1)v]
= [au + bv | -bu + av]
= Ca,b
Therefore, we conclude that G^-1MG is equivalent to the standard rotation-dilation matrix Ca,b.
Learn more about matrix here
https://brainly.com/question/30389982
#SPJ11
As monte carlo simulation is essentially statistical sampling, the larger the number of trials used, the more precise is the result.
a. True
b. False
Answers
True, Monte Carlo simulation is used for statistical sampling where larger number of trials are used for the precise result.
Step by Step Explanation:
Monte Carlo simulation is a mathematical technique or statistical sampling which is used to predict all possible outcomes of any uncertain event.The larger the number of trials more is the accuracy as it is based on the past data to predict the future outcomes.example : For the prediction of first month sale of any new launch product you can revise more number of old data.It help to calculate probability more accurately.Therefore, it is true to have more number of trials in Monte Carlo simulation statistical sampling for precise result.
Learn more about statistical sampling here
brainly.com/question/29490427
#SPJ4
HELPLPOO ASAP PLEASE HELP MEE
