Answers
Answer:
∠ 6 = 38°
Step-by-step explanation:
∠ 6 and 38° are vertically opposite angles and are congruent , then
∠ 6 = 38°
Related Questions
Natural gas is to be produced from a geologic formation confined on the top and bottom by impervious shale layers. Let φ=0.3, b=100 m,αp=4×10−9 Pa−1 and; rho=0.1hp Where rho gas density (kg/m3),hp pressure head expressed as meters of water (m). Calculate the gas mass produced if the pressure head is reduced from 100 m to 30 m over an area of 10,000 m2.
Answers
Answer:
Step-by-step explanation:
To calculate the gas mass produced, we can use Darcy's Law, which relates the flow of gas through a porous medium to the pressure gradient. The formula for Darcy's Law is:
Q = -k * A * (dP/dx)
Where:
Q is the flow rate (m^3/s)
k is the permeability of the medium (m^2)
A is the cross-sectional area (m^2)
dP/dx is the pressure gradient (Pa/m)
Given:
φ = 0.3
b = 100 m
αp = 4 × 10^(-9) Pa^(-1)
ρ = 0.1 hp (gas density)
Pressure head (initial) = 100 m
Pressure head (final) = 30 m
Area (A) = 10,000 m^2
First, we need to calculate the permeability (k) using the porosity (φ) and the compressibility (αp) as follows:
k = φ² * αp
k = 0.3² * (4 × 10^(-9) Pa^(-1))
k = 9 × 10^(-11) m^2
Next, we can calculate the pressure gradient (dP/dx) by subtracting the final pressure head from the initial pressure head and dividing it by the distance (b):
dP/dx = (Pressure head (final) - Pressure head (initial)) / b
dP/dx = (30 m - 100 m) / 100 m
dP/dx = -0.7 Pa/m
Now, we can calculate the flow rate (Q) using Darcy's Law:
Q = -k * A * (dP/dx)
Q = -9 × 10^(-11) m^2 * 10,000 m^2 * (-0.7 Pa/m)
Q = 6.3 × 10^(-4) m^3/s
Finally, we can calculate the gas mass (m) using the flow rate (Q) and the gas density (ρ):
m = Q * ρ
m = 6.3 × 10^(-4) m^3/s * 0.1 kg/m^3
m = 6.3 × 10^(-5) kg/s
Therefore, the gas mass produced when the pressure head is reduced from 100 m to 30 m over an area of 10,000 m^2 is approximately 6.3 × 10^(-5) kg/s.
To calculate the gas mass produced, Using Darcy's Law and the given values, we can determine the gas mass produced when the pressure head is reduced from 100 m to 30 m over an area of 10,000 m2.
The gas mass produced can be calculated by first determining the permeability (k) using the given values of porosity (φ), compressibility (αp), gas density (ρ), and thickness (b). With the obtained value of k, we can then use Darcy's Law to calculate the gas flow rate. However, since the time period is not specified, we cannot directly calculate the gas mass produced. The gas flow rate obtained from Darcy's Law represents the volume of gas flowing per unit time. To calculate the gas mass produced, we need to integrate the flow rate over time. Without the time component, we cannot determine the exact gas mass produced. Therefore, the calculation of the gas mass produced requires information about the time period or additional data.
Learn more about mass here:
https://brainly.com/question/11954533
#SPJ11
Which of the following equations are equivalent? Select three options. 2 + x = 5 x + 1 = 4 9 + x = 6 x + (negative 4) = 7 Negative 5 + x = negative 2
Answers
Answer:
the following 3 equations are equivalent :
• x + 1 = 4
• 2 + x = 5
• -5 + x = -2
Step-by-step explanation:
2 + x = 5
x + 1 = 4
9 + x = 6
x + (- 4) = 7
-5 + x = - 2
Let’s take this equation :
x + 1 = 4
=======
By Adding 1 to both sides of the equation we get :
x + 1 + 1 = 4 + 1
⇔ x + 2 = 5
⇔ 2 + x = 5
Then the equations x + 1 = 4 and 2 + x = 5 are equivalent.
…………………………………………………………………
On the other hand ,if we subtract 6 from both sides
of the equation x + 1 = 4 we get :
x + 1 - 6 = 4 - 6
⇔ x - 5 = -2
⇔ -5 + x = -2
Then the equations x + 1 = 4 and -5 + x = -2 are equivalent.
Answer:
A. 2 + x = 5
B. x + 1 = 4
E. -5 + x = -2
Step-by-step explanation:
right on edg, hope it helps ya'll.
Which equation represents the line that is perpendicular to the graph of 4x+3y=9 and passes through (-2,3)?
Answers
Considering the definition of perpendicular line, the equation of the perpendicular line to the graph of 4x+3y=9 and passes through (-2,3) is y= 3/4x + 9/2.
Linear equationA linear equation o line can be expressed in the form y = mx + b
where
x and y are coordinates of a point.m is the slope.b is the ordinate to the origin and represents the coordinate of the point where the line crosses the y axis.Perpendicular linePerpendicular lines are lines that intersect at right angles. If you multiply the slopes of two perpendicular lines, you get –1.
Equation of perpendicular line in this caseIn this case, the line is 4x+3y=9. Expressed in the form y = mx + b, you get:
3y= 9 - 4x
y= (-4x + 9)÷ 3
y= -4/3x +3
If you multiply the slopes of two perpendicular lines, you get –1. In this case, the line has a slope of -4/3. So:
-4/3× slope perpendicular line= -1
slope perpendicular line= (-1)÷ (-4/3)
slope perpendicular line= 3/4
The line passes through the point (-2, 3). Replacing in the expression for perpendicular line:
3= 3/4× (-2) + b
3= -3/2 + b
3 + 3/2 = b
9/2= b
Finally, the equation of the perpendicular line is y= 3/4x + 9/2.
Learn more about perpendicular line:
brainly.com/question/7197064
brainly.com/question/11470863
brainly.com/question/7280013
#SPJ1
which of the following successfully switches the integer values of the variables x and y? temp may be used as a temporary variable if necessary. x
Answers
A web server is software and hardware that uses HTTP (Hypertext Transfer Protocol) and other protocols to respond to client requests made over the World Wide Web. The main job of a web server is to display website content by storing, processing, and delivering web pages to users.
To successfully switch the values of the variables x and y using a temporary variable called "temp," you can follow these steps:
1. Assign the value of x to the temporary variable: temp = x;
2. Assign the value of y to the variable x: x = y;
3. Assign the value stored in the temporary variable (temp) to the variable y: y = temp; By following these steps, the values of the variables x and y will be switched using the temporary variable "temp."The purpose of the break statement is to break out of a loop early. For example, if the following code asks you to input an integer number, x, If x is divisible by 5, the break statement is executed, and this causes the exit from the loop.The break statement ends the loop immediately when it is encountered. Its syntax is broken. The break statement is almost always used with an if-else statement inside the loop.
Learn more about the switch: https://brainly.com/question/14883923
#SPJ11
Find the values of a and b that make the following piecewise defined function both continuous and differentiable everywhere. f(x) = 3x + 4, X<-3
2x2 + ax + b. X>-3
Answers
The values of a and b that make the piecewise defined function f(x) = 3x + 4, for x < -3, and f(x) = 2x^2 + ax + b, for x > -3, both continuous and differentiable everywhere are a = 6 and b = 9.
To ensure that the piecewise defined function is continuous at the point where x = -3, we need the left-hand limit and right-hand limit to be equal. The left-hand limit is given by the expression 3x + 4 as x approaches -3, which evaluates to 3(-3) + 4 = -5.
On the right-hand side of the function, when x > -3, we have the expression 2x^2 + ax + b. To find the value of a, we need the derivative of this expression to be continuous at x = -3. Taking the derivative, we get 4x + a. Evaluating it at x = -3, we have 4(-3) + a = -12 + a. To make this expression continuous, a must be equal to 6.
Next, we find the value of b by considering the right-hand limit of the piecewise function as x approaches -3. Substituting x = -3 into the expression 2x^2 + ax + b, we get 2(-3)^2 + 6(-3) + b = 18 - 18 + b = b. To make the function continuous, b must equal 9.
Therefore, the values of a and b that make the piecewise defined function both continuous and differentiable everywhere are a = 6 and b = 9.
Learn more about piecewise
brainly.com/question/28225662
#SPJ11
Simplify: 27w + 5w math
Answers
Answer: 32w
Step-by-step explanation:
find the directional derivative of the function at the given point in the direction of the vector v. f(x, y) = 3ex sin(y), (0, /3), v = −5, 12 dvf(0, /3) =
Answers
The directional derivative of the function f(x, y) = 3ex sin(y) at the point (0, π/3) in the direction of the vector v = (-5, 12) is ∂vf(0, π/3) = -60eπ/3.
The directional derivative measures the rate at which a function changes at a given point in a specific direction. To compute it, we need to take the dot product between the gradient vector (∇f) and the unit vector in the direction of v.
First, we need to find the gradient of f(x, y) by taking the partial derivatives with respect to x and y. The partial derivative with respect to x is ∂f/∂x = 3ex sin(y), and the partial derivative with respect to y is ∂f/∂y = 3ex cos(y).
Next, we evaluate the gradient at the point (0, π/3) by substituting x = 0 and y = π/3 into the partial derivatives. We obtain ∂f/∂x = 3e^0 sin(π/3) = (3/2)√3 and ∂f/∂y = 3e^0 cos(π/3) = (3/2).
To find the directional derivative, we take the dot product between the gradient vector (∇f) and the unit vector in the direction of v, which is v/|v|. Since v = (-5, 12), we normalize it to obtain the unit vector (-5/13, 12/13).
Finally, we compute the directional derivative as ∂vf(0, π/3) = (∇f) · (v/|v|) = [(3/2)√3, (3/2)] · (-5/13, 12/13) = -60eπ/3. Therefore, the directional derivative of f(x, y) at (0, π/3) in the direction of v is -60eπ/3.
Learn more about gradient vector here:
https://brainly.com/question/29751488
#SPJ11
On a survey, students reported how many minutes it takes them to travel to school. Here are their responses. 10,13 ,16 5,4 ,14 , Find the mean travel time for these students.
Answers
Answer:
Mean travel time = 10.33 minutes
Step-by-step explanation:
The mean of a distribution is a measure of central tendency that shows the centre of a set of data. Mathematically, it is represented as:
Mean = Sum of the terms ÷ Number of terms
Mean = (10 + 13 + 16 + 5 + 4 + 14) ÷ 6
Mean = 62 ÷ 6 = 10.33
∴ Mean travel time = 10.33 minutes
N:B 10.33 minutes = 10 minutes + 0.33 minutes
converting 0.33 minutes to seconds
1 minute = 60 seconds
∴ 0.33 minute = 60 × 0.33 = 19.8 seconds
∴ Mean time = 10 minutes 20 seconds
Pls show work in this problem
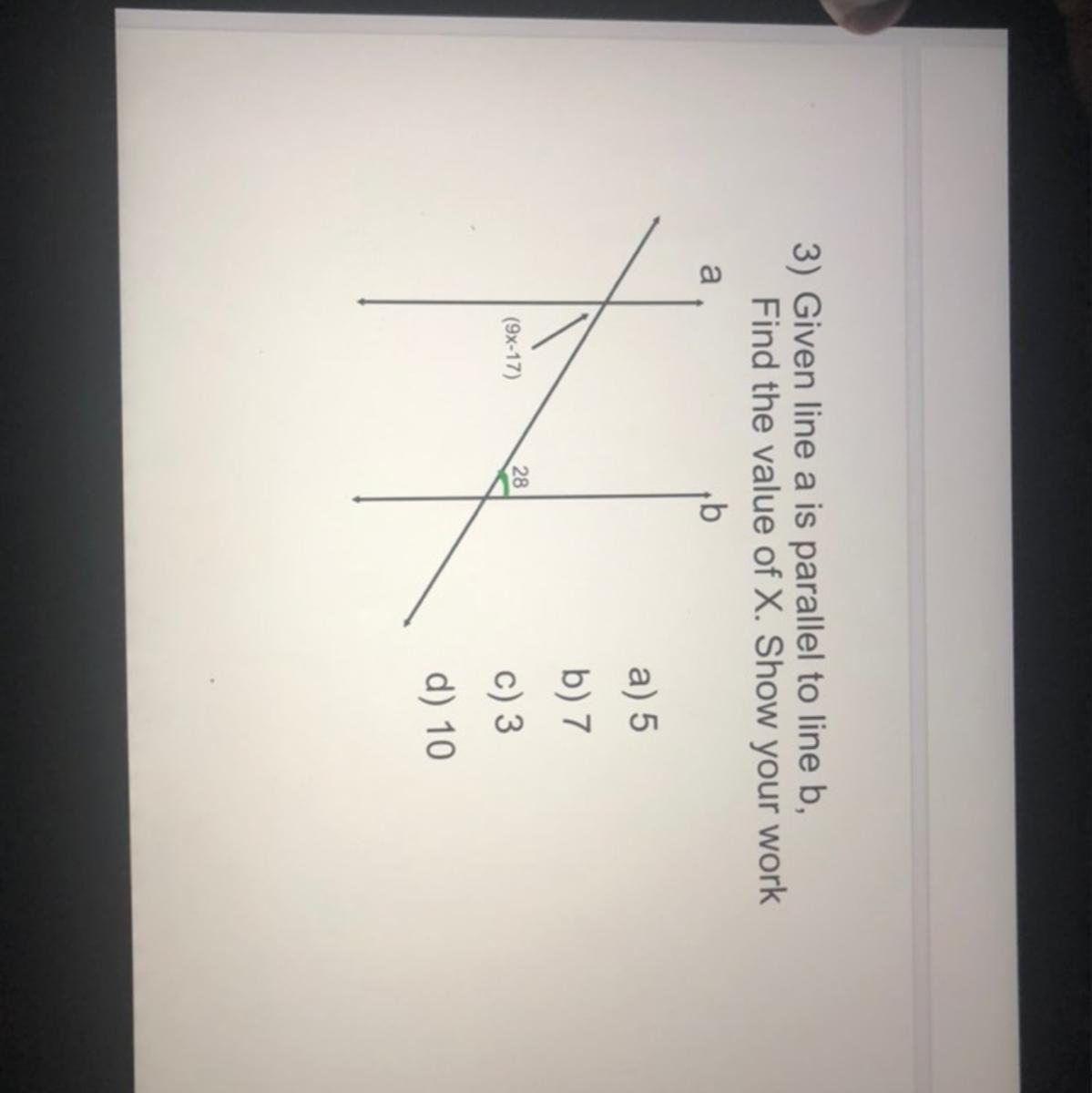
Answers
Answer:
a
Step-by-step explanation:
Given that a and b are parallel lines, then
9x - 17 and 28 are alternate angles and congruent, thus
9x - 17 = 28 ( add 17 to both sides )
9x = 45 ( divide both sides by 9 )
x = 5 → a
Each lap Jeffrey needs to run is one tenth of a mile he wants to run threee fifths of a mile how many laps does he need to run
Answers
Answer:
6 laps
Step-by-step explanation:
Each lap Jeffrey needs to run is one tenth of a mile he wants to run threee fifths of a mile how many laps does he need to run
One tenth of a mile = 1/0
Three fifths of a mile = 3/5
From the question:
1/10 mile = 1 lap
3/5 mile = x
Cross Multiply
1/10 mile × x = 3/5 mile × 1 lap
x = 3/5 mile × 1 lap/ 1/10 mile
x = 3/5 ÷ 1/10
x = 3/5 × 10/1
x = 6 laps
Therefore, for there fifths of a mile(3/5) he needs to run 6 laps
WILL GIVE BRAINLIEST
Two gears are connected and rotating at the same time. The smaller gear completes 3 2/3 rotations every time the larger gear completes 1/3 of a rotation.
How many rotations does the smaller gear complete when the larger gear completes 1 rotation?
Drag and drop the correct value into the box.
A. 1/11
B. 11/9
C. 11
D. 22
Answers
A
Let's start by finding the gear ratio which is given by the ratio of the number of teeth on the larger gear to the number of teeth on the smaller gear. Since the problem doesn't specify the number of teeth on each gear, we can assume that the gear ratio is expressed as a fraction p/q. Since the smaller gear completes 3 2/3 revolutions every time the larger gear completes 1/3 of a rotation, the gear ratio must be p/q = (11/3)/(1/3) = 11. This means that the larger gear must have 11 times as many teeth as the smaller gear.
If the larger gear completes one rotation, the smaller gear will complete 1/11 of a rotation, or 0.090909... rotations. Therefore, the smaller gear completes approximately 0.0909 rotations (or 3/33 rotations) when the larger gear completes 1 rotation.
Answer: C 11
Step-by-step explanation:
Small Gear 3 2/3 rotations for large 1/3 rotation
Ratio:
3 2/3 : 1/3 >mulitply both by 3 to make the large side =1
\((3\frac{2}{3} )(3) : \frac{1}{3} (3)\) >change 3 2/3 to improper and simplify right side
\(\frac{11}{3} (3) : 1\) >simplify
11 : 1
Interpretation:
The left side was the small gear and right side was large gear. Now we have the ratio that says the small gear will rotate 11 times for every 1 time the large gear rotates.
This makes sense because a small gear will rotate more times vs. a big one.
recall that hexadecimal numbers are constructed using the 16 digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f. (a) how many strings of hexadecimal digits consist of from one through three digits?
Answers
There are a total of 4,368 strings of hexadecimal digits consisting of one through three digits .
To determine the number of strings of hexadecimal digits consisting of one through three digits, we can analyze each case separately:
Strings with one digit:
In this case, we can choose any of the 16 available digits (0-9, a-f) to form a single-digit string. Therefore, there are 16 possibilities for one-digit strings.
Strings with two digits:
Here, we can select any digit from 0-9 or a-f for the first digit, and similarly for the second digit. This gives us 16 choices for each digit, resulting in a total of 16 × 16 = 256 possibilities for two-digit strings.
Strings with three digits:
Similar to the previous case, we have 16 choices for each of the three digits. Therefore, the total number of three-digit strings is 16 16 × 16 = 4,096.
To find the total number of strings of hexadecimal digits consisting of one through three digits, we sum up the possibilities for each case:
Total = (number of one-digit strings) + (number of two-digit strings) + (number of three-digit strings)
= 16 + 256 + 4,096
= 4,368
Therefore, there are a total of 4,368 strings of hexadecimal digits consisting of one through three digits.
To know more about hexadecimal digits click here
https://brainly.com/question/32676402
#SPJ4
Ella Bell operates a company that buys and sells tickets to sporting events. She deposits the day's receipts into her savings account. In bills, she had 52 one hundreds, 21 fifties, 19 tens, 71 fives, and 63 ones. Change included 6 one-dollar coins, 60 fifty-cent pieces, 32 quarters, 121 dimes, and 165 pennies. She also deposited checks for $29.44, $125.65, and $45.94. She wants to receive 5 two-dollar bills in cash.
Answers
The total deposits of Ella Bell based on the information is $ 7,107.38
How to calculate the deposit?From the information, Ella Bell operates a company that buys and sells tickets to sporting events. She deposits the day's receipts into her savings account.
In bills, she had 52 one hundreds, 21 fifties, 19 tens, 71 fives, and 63 ones. Change included 6 one-dollar coins, 60 fifty-cent pieces, 32 quarters, 121 dimes, and 165 pennies. She also deposited checks for $29.44, $125.65, and $45.94. She wants to receive 5 two-dollar bills in cash.
This will be:
= Currency + Coins + Checks - Cash received
= 6858 + 57.75 + 201.63 - 10
= 7107.38
Learn more about deposit on:
https://brainly.com/question/25787382
#SPJ1
the cost that varies depending on the values of the decision variables is a
Answers
A cost that varies depending on the values of decision variables is a variable cost. This type of cost changes in proportion to changes in the production or sales volume.
Variable costs are expenses that fluctuate with changes in the level of production or sales. These costs are directly tied to the quantity of goods or services produced or sold, and they increase or decrease as the production or sales volume changes. Common examples of variable costs include materials, labor, and direct expenses associated with producing a product or providing a service. As the production or sales volume increases, the variable cost per unit decreases, due to economies of scale. Conversely, as production or sales volume decreases, the variable cost per unit increases, due to diseconomies of scale. Understanding variable costs is essential for businesses to accurately calculate their costs of goods sold, determine their break-even point, and make informed decisions about pricing and production levels.
Learn more about volume here: https://brainly.com/question/28058531
#SPJ11
Please help thank you

Answers
calculate the surface area of the cylinder.
A. 351.9 cm²
B. 500 cm³
C. 140.4 cm²
D 301.7 cm²

Answers
2 x pi x r x h + 2 x pi x r^2
SA = 2 x pi x 4 x 10 + 2 x pi x 4^2
= 351.9 cm^2
Hope this helps!!
Evaluate f(x) = x^2 + 4 for x = -3
Answers
f(x)=9+4
f(x)=13
Hope my answer helped u :)
Rewrite the expressions below by completing the square
2 + 4+ 1
Answers
(Mark brainliest pls)
Square root is 2 square + 4 square + 1 because 1 does not enable a square perhaps for negatives to be imputed, and we know 2 square will be 1 hence,
1 x 1 = 1 squared
2 x 2 = 4 squared
Perhaps for 1, you will have to use a formula equation and add tang maybe. Etc I don’t know if tang but u will also have to convert 1 to a decimal to find the square root of 1, 1 is an odd number so it will end up with remainder decimals or just do 1x1, etc.
Hence u
(2 square + 4 square) + 1square?
It depends on addition or order of operations subtraction addition or you will might use multiply
if the subject is about multiply or Division so try and do it because i don’t know if I’m right
..
REMEMBER
PEMDAS
Please Excuse My Dear Aunt Sally
Parentheses
Equations
Multiplication
Division
Addition
Subtraction
ORDER OF OPERATIONS.
try and solve it hope this helps!
Have a nice day
graph ksjfkdkdkdkdkfkfk

Answers
Answer:
See attachment >_<
Step-by-step explanation:
Because the line includes the point \((0,3)\), we'll begin our line at this coordinate.
The slope is \(7\), or, \(\frac{7}{1}\). Slope is formatted in the \(rise\) in the line over its \(run\). Or, \(\frac{rise}{run}\). This means the line rises \(7\) units and runs \(1\) unit.
From our beginning point, \((0,3)\), move up seven units and then to the right one unit.
If this line was negative (it would have a negative slope), we would run to the left. However, we have a positive slope, so we will run to the right.
By doing this, we land on the point \((1,10)\). Draw a line through this point with our beginning coordinate \((0,3)\). This is our graphed line. I've attached a photo as well :)
Good luck ^^

Answer:
the answer is the 3rd one down fnivjgoibjmvkmkfmvk
Step-by-step explanation:
3. Solve your equation to find the distance Jane’s trainer bikes. Show your work.
4. How much farther does Jane travel than her trainer?
(my previous answers so this will make sense)
1. The total distance jane bikes and runs is 28 miles.
2. Janes trainer bikes a distance of 20 miles.
Answers
Jane travels 8 miles much farther than her trainer. The solution is obtained using arithmetic operations.
What are arithmetic operations?
By combining operands with one arithmetic operator, an arithmetic operation is given. The built-in functions add, subtract, divide, and multiply additionally allow for the specification of arithmetic operations.
3. Using pythagoras theorem, we get the equation as D² = 12² + 16².
⇒D² = 144 + 256
⇒D² = 400
⇒D = √400
⇒D = 20
4. Jane has traveled 28 miles in total whereas her trainer has traveled 20 miles.
So, the difference is 28-20= 8 miles
Hence, Jane travels 8 miles much farther than her trainer.
Learn more about arithmetic operations from the given link
https://brainly.com/question/30283549
#SPJ1
27) Select the collection of sets that forms a partition of: {1,2,3,4,5,6,7,8} a. {1,2,5,7} {3,4} \{8\} b. {1,2,5,7} {3,4,6} {8} c. {0,1,2,5,7} {3,4,6,8} d. {1,2,5,7} {3,4,6,8} {2,4} 28) Select the collection of sets that forms a partition of: {a,b,c,d,e,f,g} a. {a,b,c,e,f,g} b. {a,b,c,d} {e,f,g,h} c. {a,c,d,g} {b,e,f} ∅ d. {a,c,e,g} {b,f} {d}
Answers
27)Option (b) {1,2,5,7} {3,4,6} {8} 28)Option (c) {a,c,d,g} {b,e,f} ∅
27) The collection of sets that forms a partition of {1,2,3,4,5,6,7,8} is:
Option (b) {1,2,5,7} {3,4,6} {8}
In set theory, a partition of a set is a set of non-empty subsets of the set where no element appears in more than one subset.
That is, a partition is a decomposition of the set into disjoint non-empty subsets, where all the subsets combined result in the whole set.
28) The collection of sets that forms a partition of {a,b,c,d,e,f,g} is:
Option (c) {a,c,d,g} {b,e,f} ∅
Learn more about Set Theory:
brainly.com/question/13458417
#SPJ11
a submarine dives below the surface, heading downward in three moves.if each move downward was 325 feet, where is the submarine after it is finished diving
Answers
Answer:
975 feet
Step-by-step explanation:
325 + 325 + 325 or 325 multiplied 3 times is 975
What are the 5 examples of linear equation?.
Answers
The required five equation of linear equation are given below.
What is linear equation?A linear equation is a mathematical condition of the structure y=mx+b. including just a steady and a first-request (straight) term, where m is the incline and b is the y-catch. At times, the above is known as a "direct condition of two factors," where y and x are the factors.
According to question:Five examples of linear equation,
1) 2x – 3 = 0
2) 2y = 8
3) m + 1 = 0
4) x/2 = 3
5) x + y = 2
To know more about linear equation visit:
brainly.com/question/11897796
#SPJ4
Let u1 = [ 1 , 0 , -5 , 2 ]u2 = [ 0 , -1 , 2 , 5 ]u3 = [ 5 , 2 , 1 , 0 ]u4 = [ 2 , -5 , 0 , -1 ]AND Let W1 = Span {u1 , u2} , Let W2 = Span {u3 , u4}.write the vector y = 2 8 4 −6 as a sum of a vector in w1 and a vector in w2.
Answers
To write the vector y = [2, 8, 4, -6] as a sum of a vector in W1 and a vector in W2, we need to find the scalar multiples of vectors u1 and u2 that can be added to scalar multiples of vectors u3 and u4 to obtain y.
Let's find the scalar multiples of u1 and u2 first:
a1u1 + a2u2 = [2, 8, 4, -6]
We can solve this system of equations to find the values of a1 and a2:
a1 + 0 = 2 --> a1 = 2
0 + (-a2) = 8 --> a2 = -8
-5a1 + 2a2 = 4 --> -5(2) + 2(-8) = 4 --> -10 - 16 = 4 --> -26 = 4 (not satisfied)
2a1 + 5a2 = -6 --> 2(2) + 5(-8) = -6 --> 4 - 40 = -6 --> -36 = -6 (not satisfied)
Since the last equation is not satisfied, we cannot write y as a sum of a vector in W1 and a vector in W2.
Therefore, there is no solution to this problem. The vector y cannot be expressed as a sum of a vector in W1 and a vector in W2.
learn more about multiples here
https://brainly.com/question/14059007
#SPJ11
just wondering if anyone wanted to play with me
Im only at young age so dont be mean to me :c
Answers
And lots more games just name one
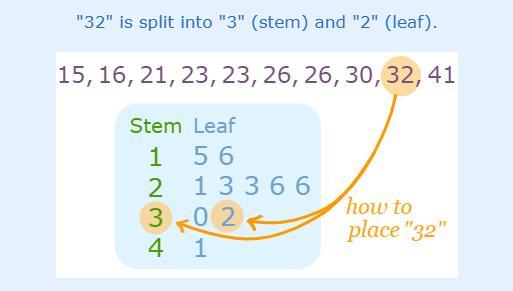
The stemplot below represents the distribution of math test scores for aninth-grade algebra course. What was the highest score received?

Answers
Explanation
We are given the stemplot below:
We are required to determine the highest score received.
A stemplot can be interpreted as follows:
With the illustration above, we can pair the stem and leaf of the stemplot given to determine that the highest score is 100.
Option B is correct. The answer is 100.

n × 9 = 0 true? please i will give 25 points?
Answers
Answer:
This can be true if n=0
Step-by-step explanation:
9n = 0
Divide each side by 9
9n/9 = 0/9
n=0
This can be true if n=0
Veronica has a box that contains 24 pictures of her family, 6 pictures of her dog, and 12 pictures of her friends. Veronica randomly chooses one picture from the box. Which statement best describes what will likely happen.
A. She will definitely pick a picture of her family
B. She will most likely pick a picture of her family
C. She is equally likely to pick a picture of her family or of her dog
D. She is equally likely to pick a picture of her family, of her dog or of her friends
Answers
Select the correct answer. What is the sum of the first 17 terms of this arithmetic series? Use Sn=n(a1+an/2) .
-28 + (-13) + 2 + 17 + ⋯
A. 1,692 B. 1,564 C. 227 D. 212
Answers
Answer:
1564.
Step-by-step explanation:
First term = -28 and common difference = 15.
Sum = (17/2)(2*-28 + (17-1)15)
= 8.5 * 184
= 1564.
An equation 3 (2x - 7) = 3
Part A: How many solutions does this equation have?
Part B: What are the solutions to this equation? Show your work.
Answers
The solution of the equation 3(2x - 7) = 3 is x = 4 and the equation has a single solution.
How to solve equation?Equations are mathematical statements containing two algebraic expressions on both sides of an 'equal to (=)' sign.
Therefore, let's solve the equation as follows:
3(2x - 7) = 3
open the bracket
3(2x - 7) = 3
6x - 21 = 3
add 21 to both sides of the equation
6x - 21 = 3
6x - 21 + 21 = 3 + 21
6x = 24
divide both sides by 6
6x / 6 = 24 / 6
x = 4
Therefore, the equation has only one solution. The solution of the equation is x = 4.
learn more on equation here: https://brainly.com/question/12569013
#SPJ1
