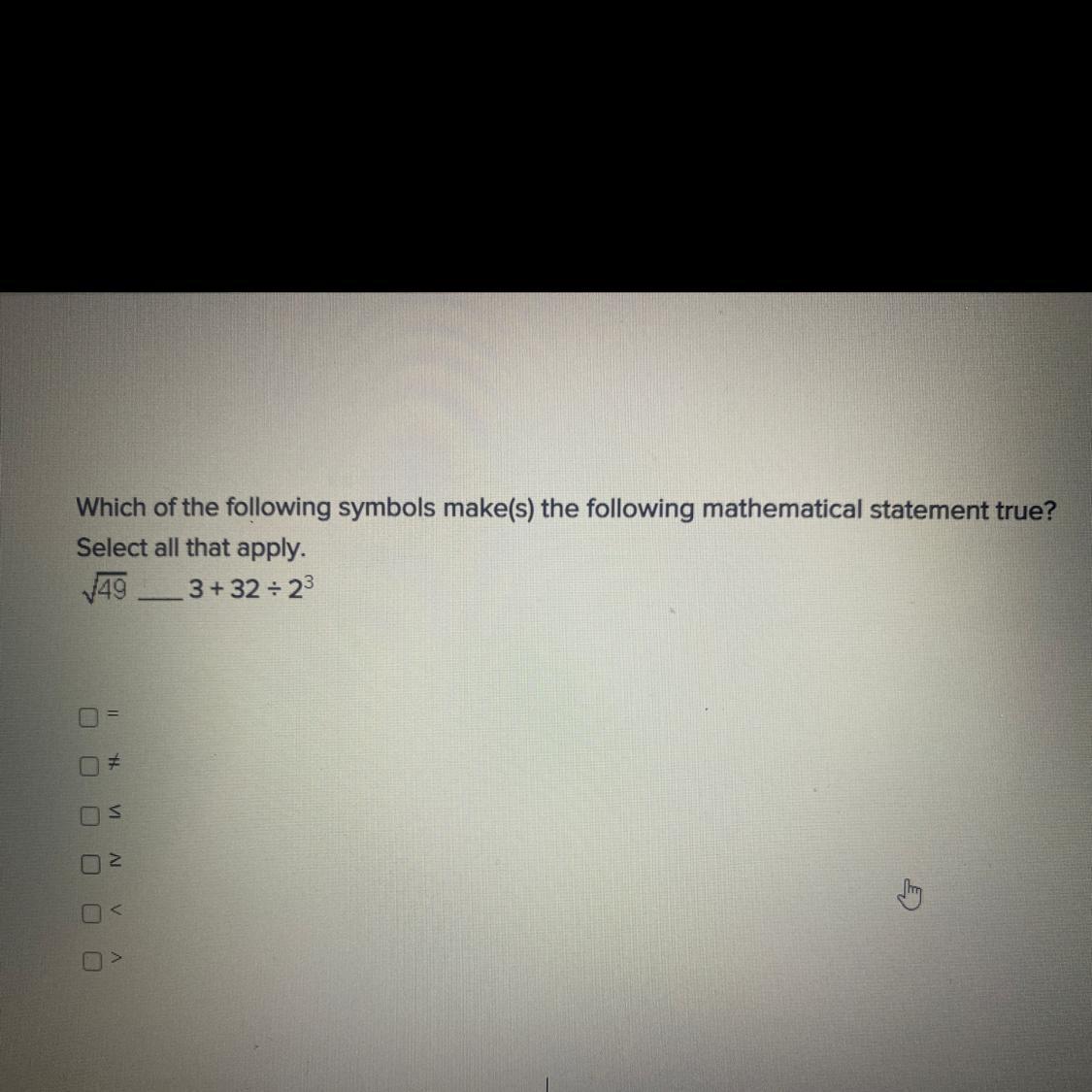
James has $40 to spend. He wants to buy 2 tickets to a show. He has to spend $7 to get where tickets are sold. The following inequality can be used to find out the highest price James can afford to pay for each ticket. 2x+7 less than or equal to 40.
A.) x less than or equal to 23.5
B.) x less than or equal to 16.5
C.) x greater than or equal to 23.5
D.) x greater than or equal to 16.5

Answer:

54 Hours

Step-by-step explanation:

first of all 540-54 he started with is 486 and 486/9 is 54 since you get 9 per hour

Answer: 54 Hours of babysitting

Step-by-step explanation: 540-54=486 Then you take 486 and you divide it by 9 to see how many hours you have to work and that would be 54 hours.

The distance from the center of dilation, Q, to the image of vertex A will be 4 units.

According to the given rule of dilation, D subscript Q, two-thirds, the triangle ABC will be dilated with a scale factor of two-thirds centered at point Q.

Since point Q is the center of dilation and the distance from triangle ABC to point Q is 6 units, the image of vertex A will be 2/3 times the distance from A to Q. Therefore, the distance from A' (image of A) to Q will be (2/3) x 6 = 4 units.

By applying the scale factor to the distances, we can determine that the length of A'B' is (2/3) x  3 = 2 units, the length of B'C' is (2/3) x 7 = 14/3 units, and the length of A'C' is (2/3) x 8 = 16/3 units.

Thus, the distance from the center of dilation, Q, to the image of vertex A is 4 units.

For more such answers on the Center of dilation
https://brainly.com/question/13173812

#SPJ8

Answer:

-4.8

Step-by-step explanation:

-24/5 = (-24) \(\div\) 5

= -4.8

Answer:

The answer is -4.8

Step-by-step explanation:To get -24/5 into a decimal you simply divide 24 by 5.

Answer:

At my school 20 people boys and girls play soccer

Given: A quadratic equation,

Required: To transform the equation by completing the square.

Explanation: The general quadratic equation of the form,

can be transformed into a complete square by adding and subtracting the following term,

Hence, adding 4 and subtracting 4 from the given equation,

Now the equation can be transformed as follows,

or,

Final Answer: The

Using the properties of logarithms, we can write:

In(4x^2 - 48x + 128) = In(4(x^2 - 12x + 32))
= In(4) + In(x^2 - 12x + 32)
= 2ln(2) + In((x - 8)(x - 4))

We can't simplify (x - 8)(x - 4) any further, so the final answer is:

In(4x^2 - 48x + 128) = 2ln(2) + In((x - 8)(x - 4))

To expand the given expression ln(4x^2 - 48x + 128) using the properties of logarithms, we first need to factor the quadratic expression inside the natural logarithm function.

Expression: ln(4x^2 - 48x + 128)

Step 1: Factor out the common factor, which is 4.
ln(4(x^2 - 12x + 32))

Step 2: Factor the quadratic expression inside the parentheses.
(x^2 - 12x + 32) = (x - 4)(x - 8)

So, the factored expression is ln(4(x - 4)(x - 8)).

Now, we can use the properties of logarithms to expand the expression.

Step 3: Apply the logarithm product rule, ln(a * b) = ln(a) + ln(b).
ln(4(x - 4)(x - 8)) = ln(4) + ln(x - 4) + ln(x - 8)

The expanded expression is ln(4) + ln(x - 4) + ln(x - 8). There are no further numerical expressions that can be simplified without a calculator.

Your answer: ln(4) + ln(x - 4) + ln(x - 8)

Learn more about :

properties of logarithms : https://brainly.com/question/30226560

#SPJ11

Answer:

x = sqrt(11 - y) - 2 or x = -sqrt(11 - y) - 2

Step-by-step explanation:

Solve for x:

y = -x^2 - 4 x + 7

y = -x^2 - 4 x + 7 is equivalent to -x^2 - 4 x + 7 = y:

-x^2 - 4 x + 7 = y

Multiply both sides by -1:

x^2 + 4 x - 7 = -y

Add 7 to both sides:

x^2 + 4 x = 7 - y

Add 4 to both sides:

x^2 + 4 x + 4 = 11 - y

Write the left hand side as a square:

(x + 2)^2 = 11 - y

Take the square root of both sides:

x + 2 = sqrt(11 - y) or x + 2 = -sqrt(11 - y)

Subtract 2 from both sides:

x = sqrt(11 - y) - 2 or x + 2 = -sqrt(11 - y)

Subtract 2 from both sides:

Answer: x = sqrt(11 - y) - 2 or x = -sqrt(11 - y) - 2

Answer: D.

Step-by-step explanation:

You can start out with the form AX = B and solve for matrix X that would yield the answer

Then X = (A^-1)(B)

A = [1    -1]

      [1     1]

A^-1 = (1/(1 - (1)(-1)))*[1    1]

                             [-1   1]

which can be written as (1/2) * [1    1]

                                                  [-1   1]

B = [26]

     [6]

(A^-1)(B) = (1/2)*[1    1] [6]

                        [-1   1] [26]

= (1/2)*[32]

          [20]

= [16]

  [10]

Answer:

-12/6 or -2

Step-by-step explanation:

Answer:

-2

Step-by-step explanation:

Gradient = slop

(-3,6)

(3,-6)

\(gradient \: = \frac{difference \: of \: y \: }{difference \: of \: x} \)

\(gradient \: = \frac{6 - ( - 6)}{ - 3 - 3} \)

= 12/-6

= - 2

Answer:

Step-by-step explanation:

it would be a 20% tip

Answer:

3.75

Step-by-step explanation:

5% of 75 is 3.75

Answer:

id

Step-by-step explanation:idk

Answer:

Step-by-step explanation:

ez

Answer:

Step-by-step explanation:

The correct answer is d. the chi-square test compares the difference between expected and observed frequency counts.

The chi-square test is a statistical test used to analyze the distribution of categorical data. It compares the observed frequency counts of a categorical variable with the expected frequency counts.

The expected frequency counts are calculated based on a null hypothesis, which assumes that there is no significant difference between the observed and expected frequencies.

The test statistic for the chi-square test is calculated as the sum of the squared differences between the observed and expected frequency counts, divided by the expected frequency counts.

The resulting value is compared to a chi-square distribution with a certain number of degrees of freedom to determine the p-value and assess the significance of the observed difference.

Therefore, options a, b, and c are incorrect because they describe other types of statistical tests that are used to compare means or variances between groups, while the chi-square test is specifically designed for analyzing categorical data.

To know more about  chi-square test refer here

https://brainly.com/question/14082240#

#SPJ11

Answer:

$600

Step-by-step explanation:

20*30= 600

The difference between the polynomials 9x² + 8x and 2x² + 3x is 7x² + 5x.

A polynomial is formed mathematically by combining one or more algebraic terms (monomials). The roots of "polynomial" are poly- (many) and -nomial (terms). A polynomial can have exponents (powers), constants (numbers), and variables (letters), but not negative exponents or variable division.

Polynomials are typically expressed in standard form. Furthermore, because there are no similar terms among the exponents, they are arranged in descending order (largest to smallest).

To find the difference between

(9x² + 8x) - (2x² + 3x)

We do calculation

= 9x² + 8x - 2x² - 3x

= 9x² - 2x² + 8x - 3x

= 7x² + 5x

Thus, the difference between the polynomials is 7x² + 5x.

Learn more about polynomials

https://brainly.com/question/11536910

#SPJ4

The critical values for a 90% confidence level with a sample size of n=15 are χ²₀.₀₅=22.307 and χ²₀.₉₅=7.260.

To find the critical values for a chi-square distribution, we need to determine the values of χ²₁−α/₂ and χ²ₐ/₂, where α is the significance level and n is the sample size.

Determine the degrees of freedom (df).

For a chi-square distribution, the degrees of freedom are calculated as df = n - 1, where n is the sample size. In this case, n = 15, so df = 15 - 1 = 14.

Determine the critical values.

The critical values are obtained from the chi-square distribution table or can be calculated using statistical software.

For a 90% confidence level, the significance level α is equal to 1 - confidence level = 1 - 0.90 = 0.10. Half of the significance level is α/2 = 0.10/2 = 0.05.

Using the degrees of freedom (df = 14) and the significance level (α/2 = 0.05), we can find the critical values.

The critical value χ²₁−α/₂ corresponds to the upper tail of the distribution. From the chi-square distribution table or software, at df = 14 and α/2 = 0.05, the value is χ²₀.₀₅ = 22.307.

The critical value χ²ₐ/₂ corresponds to the lower tail of the distribution. At df = 14 and α/2 = 0.05, the value is χ²₀.₉₅ = 7.260.

Therefore, for a 90% confidence level with a sample size of n = 15, the critical values are χ²₀.₀₅ = 22.307 and χ²₀.₉₅ = 7.260.

For more questions like Sample click the link below:

https://brainly.com/question/30759604

#SPJ11

First, regarding the simple way to find the horizontal asymptote.

The location of the horizontal asymptote depends on the function. For example, the function f(x) = 1/x has a horizontal asymptote at y=0.

The step-by-step answer

1. Identify the function's degree (highest power of x) in the numerator and the denominator.
2. Compare the degrees of the numerator and denominator:

  a) If the degree of the numerator is less than that of the denominator, the horizontal asymptote is y=0.
  b) If the degrees are equal, divide the leading coefficients to find the horizontal asymptote: y=(leading coefficient of numerator)/(leading coefficient of the denominator).
  c) If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.

For example, consider the function f(x) = (2x^2 + 3)/(x^2 - 5x + 6). The degrees of the numerator and denominator are both 2. Divide the leading coefficients: y = 2/1. So, the horizontal asymptote is y=2.

We've subtracted each given quantity from 0 and found their respective differences. So, the result of the subtraction is -3x + 16y + z - 16.

To subtract, we need to find the difference between two quantities. Let's start with the first line:
- Subtracting +9 from 0 would give us -9.
- Subtracting 5 from 0 would give us -5.
- Subtracting N from 5x - 8y would give us 5x - 8y - N.
- Adding 9 to 2 would give us 11.
Now, let's move on to the second line:
- Subtracting 8y from 0 would give us -8y.
- Multiplying 8 by -y would give us -8y.
- Subtracting 16y from -8y would give us -24y.
- Adding 2 and 9 would give us 11.
Finally, on the last line:
- Subtracting Z from 0 would give us -Z.
- Adding 9 to 0 would give us 9.
In summary, we've subtracted each given quantity from 0 and found their respective differences.
let's organize the given terms:
1. 8x - 8y
2. 5
3. 5x - 8y
4. 3x + 2 + 9
5. 3x - 16y - 2 + 9
6. 3x - z + 9
Subtracting these terms, we get:
(1)-(2)-(3)-(4)-(5)-(6) =
(8x - 8y) - 5 - (5x - 8y) - (3x + 2 + 9) - (3x - 16y - 2 + 9) - (3x - z + 9)
Combining like terms, we get:
-3x + 16y - 5 - 11 + z = -3x + 16y + z - 16
So, the result of the subtraction is -3x + 16y + z - 16.

To know more about Subtract visit:

https://brainly.com/question/2346316

#SPJ11

Step-by-step explanation:

Let x be the amount invested at 6% so that 18000-x is the amount invested at 7.5% both in dollars.

The total interest in 3 years is $3330 so we can write: 0.06x(3)+0.075(18000-x)(3)=3330

Solve for x:

0.06x(3)+0.075(18000−x)(3)=3330

Step 1: Simplify both sides of the equation.

0.06x(3)+0.075(18000−x)(3)=3330

0.06x(3)+−0.225x+4050=3330(Distribute)

0.18x+−0.225x+4050=3330

(0.18x+−0.225x)+(4050)=3330(Combine Like Terms)

−0.045x+4050=3330

−0.045x+4050=3330

Step 2: Subtract 4050 from both sides.

−0.045x+4050−4050=3330−4050

−0.045x=−720

Step 3: Divide both sides by -0.045.

−0.045x/−0.045=−720/−0.045

x=16000

x=16000

So, the amounts borrowed are:

Bank at 6% = 16000

Bank at 7.5% = 2000

Based on the given information, Abi should choose the Highbrook savings account as it will give her a higher return on her investment at the end of 3 years.

The Highbrook account has a higher initial interest rate of 2.1% for the first year, which is almost double that of the Savemore account. Although the interest rate decreases to 0.95% for the following years, the overall average interest rate for the 3-year period will still be higher than that of the Savemore account.

To calculate the total return on investment for each account, we can use the compound interest formula: A = P(1+r/n)ⁿ, where A is the final amount, P is the principal amount, r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years.

For the Savemore account, Abi will earn 1.25% compound interest each year, so after 3 years, her investment will grow to:

A = 5000(1+0.0125/1)³ = £5,196.09

For the Highbrook account, Abi will earn 2.1% compound interest for the first year and 0.95% for the following 2 years, so after 3 years, her investment will grow to:

A = 5000(1+0.021/1)¹ × (1+0.0095/1)² = £5,269.58

Therefore, Abi should choose the Highbrook savings account as it will give her a higher return on investment of £73.49 after 3 years compared to the Savemore account.

You can learn more about investment at: brainly.com/question/15353704

#SPJ11

Answer:

The quadratic x2 − 5x + 6 factors as (x − 2)(x − 3). Hence the equation x2 − 5x + 6 = 0

has solutions x = 2 and x = 3.

Similarly we can factor the cubic x3 − 6x2 + 11x − 6 as (x − 1)(x − 2)(x − 3), which enables us to show that the solutions of x3 − 6x2 + 11x − 6 = 0 are x = 1, x = 2 or x = 3. In this module we will see how to arrive at this factorisation.

Polynomials in many respects behave like whole numbers or the integers. We can add, subtract and multiply two or more polynomials together to obtain another polynomial. Just as we can divide one whole number by another, producing a quotient and remainder, we can divide one polynomial by another and obtain a quotient and remainder, which are also polynomials.

A quadratic equation of the form ax2 + bx + c has either 0, 1 or 2 solutions, depending on whether the discriminant is negative, zero or positive. The number of solutions of the this equation assisted us in drawing the graph of the quadratic function y = ax2 + bx + c. Similarly, information about the roots of a polynomial equation enables us to give a rough sketch of the corresponding polynomial function.

As well as being intrinsically interesting objects, polynomials have important applications in the real world. One such application to error-correcting codes is discussed in the Appendix to this module.

Step-by-step explanation:

Answer: 27:1

Step-by-step explanation:

The ratio of the volumes is equal to the cube of the ratio of the altitudes.

Answer:

Using Pythagorean theorem a2 + b2 = c2 15002 + 20002 = C2; c is 2,500 feet

Note that based on the quartiles the estimated number  of rides less that 6.5 minutes long is about about 5 rides.

To  estimate the number of rides that would  be less than 6.5 minutes long, we can make use of the  interquartile range (IQR).

Assumption -  Data is Symmetrically distributed.

Recall  that IQR is the variance between the first quartile (Q1) and the third quartile  (Q3).

So IQR =   Q3 - Q1

= 10 minutes - 6.5 minutes

= 3.5 minutes

Based on the assumption above  we can consider Q2 as the 50th percentile.

Thus, to estimate the number of rides that would be less than 6.5 minutes long, use the Z-score formula:

Z = (X - μ) / σ

Where:

Z is the Z-score,

X is the value we want to estimate (6.5 minutes),

μ is the mean of the data (which we assume to be Q2),

σ is the standard deviation of the data (which we assume to be IQR / 1.35).

NOte: The factor 1.35 is an approximation for converting the IQR to the standard deviation of a  normal distribution

Z = (6.5 -8) / (3.5 /1.35)

= - 0.5 / 2.59    

 =  -0.57857142857

≈ - 0.58

Based on  statistical calculator,  the proportion of data that falls below a Z-score o - 0.58, which represents the expected number of rides that would be less than 6.5 minutes long, is

= 0.2787.

Thus, te estimated number of rides less than 6.5 minutes long ≈ 0.2787 * 16

= 4.4592

≈ 4.5 rides

Thus we can expect the 4 or 5 rides to be less than 6.5 minutes long.

Learn more about quartiles:
https://brainly.com/question/24329548
#SPJ1

Answer:

3x^2+3x-6

Step-by-step explanation:

Answer:

y=3/4x+(-2) aka the first blank is 3/4 the second blank is -2

Step-by-step explanation:

The first blank is the slope, the second one shows the y-intercept. You are welcome

Answer:

A)

Given that,

On each trial, the machine outputs a ball with one of the digits 0 through 9 on it.

To find the probability of getting 6.

In each trail the probability of getting 6 is,

Let X be the event of getting 6.

we get

we get,

where n=50 and r=8

n is the total number of trials

r is the sucess trail.

Substitute the values we get,

Hence the required probability is,

On simplifying we get,

Answer is: 0.06

\((x - 5) = 12 \\ = > x = 12 + 5 \\ = > x = 17\)

The answer is 17.

Answer:

The equation for the nth term of the arithmetic sequence is:

\(a_{n} = a + (n-1)d\\\)

The \(a_{30}\) is 140

Step-by-step explanation:

"a" represents the first term which is -5.

"d" represents the common difference which is 5.

To find the common difference, just subtract the 2nd and 1st term.

0 - (-5) = 5

Now put the values in the equation:

\(a_{n} = a + (n - 1)d\\a_{n} = (-5) + (n - 1)5\)

We are finding the 30th term so just put 30 to the "n" to help us find the 30th term of the sequence.

\(a_{30} = -5 + (30-1)5\\a_{30} = -5 + (29)5\\a_{30} = -5 + 145\\a_{30} = 140\)

So the 30th term is 140