If ABC is an equilateral triangle, then the mA =60
A. If the mA = 60, then ABC is an equilateral triangle.
B. If ABC is not an equilateral triangle, then the mA does not equal 60.
C. If the mA does not equal 60, then ABC is not an equilateral triangle.
Answer is C!
Answers
The true statement from the given options is C. If the mA does not equal 60, then ABC is not an equilateral triangle.
Equilateral triangle:An equilateral triangle is one in which the angles and all three sides are equal. An equilateral triangle is also called an equiangular triangle since each of its angles has a value of 60 degrees.
The equal angle in an Equilateral triangle = 60°
Here we have 3 options
A. If the mA = 60, then ABC is an equilateral triangle.
B. If ABC is not an equilateral triangle, then the mA does not equal 60.
C. If the mA does not equal 60, then ABC is not an equilateral triangle.
Here we need to justify which of the given point will be true in the case of Equilateral Triangles.
Given
Option A: If the mA = 60, then ABC is an equilateral triangle.
With the measurement of A = 60°, here we can't conclude that ABC is an equilateral triangle because there is a possibility that the remaining angles are not equal to 60°
Option B: If ABC is not an equilateral triangle, then the mA does not equal 60.
Any type of triangle can have an angle that is equal to 60° so the given statement is wrong.
Option C. If the mA does not equal 60, then ABC is not an equilateral triangle.
As we know each angle of an equilateral triangle is 60°, So it is true that If the mA does not equal 60, then ABC is not an equilateral triangle.
Therefore,
The true statement from the given options is C. If the mA does not equal 60, then ABC is not an equilateral triangle.
Learn more about the Equilateral triangle at
https://brainly.com/question/9251073
#SPJ1
Related Questions
the length of the path described by the parametric equations x=cos^3t and y=sin^3t
Answers
The length of the path described by the parametric equations
is 3/2units.
What is the length of the path described by the given parametric equations?We can find the length of the path described by the parametric equations x=cos³t and y=sin³t by using the arc length formula.
The arc length formula for a parametric curve given by:
x=f(t) and y=g(t) is given by:
L = ∫[a,b] √[f'(t)² + g'(t)²] dt
where f'(t) and g'(t) are the derivatives of f(t) and g(t), respectively.
In this case, we have:
x = cos³t, so x' = -3cos²t sin t
y = sin³t, so y' = 3sin²t cos t
Therefore,
f'(t)² + g'(t)² = (-3cos²t sin t)² + (3sin²t cos t)²
= 9(cos⁴t sin²t + sin⁴t cos²t)
= 9(cos²t sin²t)(cos²t + sin²t)
= 9(cos²t sin²t)
Thus, we have:
L = ∫[0,2π] √[f'(t)² + g'(t)²] dt
= ∫[0,2π] √[9(cos²t sin²t)] dt
= 3∫[0,2π] sin t cos t dt
Using the identity sin 2t = 2sin t cos t, we can rewrite the integral as:
L = 3/2 ∫[0,2π] sin 2t dt
Integrating, we get:
L = 3/2 [-1/2 cos 2t] from 0 to 2π
= 3/4 (cos 0 - cos 4π)
= 3/2
Therefore, the length of the path described by the parametric equations x=cos³t and y=sin³t is 3/2 units.
Learn more about Parametric curves
brainly.com/question/15585522
#SPJ11
Several friends (Calvin, Dean, Kelli, and Lee) went to Cal's Late Night Diner for a bite to eat. Match each person to their drink (Iced tea, Lemonade, Root Beer, and Water) and determine how much each paid ($4.99, $5.99, $6.99, and $7.99) for their meal.
Clues:
1. The Diner who paid $4.99 was either Calvin or the one who got the Root Beer.
2. Kelli paid $6.99
3. The one who got the water paid 1 dollar less than Dean.
4. Calvin paid more than Lee.
5. The one who got the Root beer paid 1 dollar less than the one who got the Iced Tea.
Answers
Based on the given clues, we can determine the person, drink, and price paid for each individual:
Calvin: Root Beer, $4.99
Dean: Lemonade, $7.99
Kelli: Water, $6.99
Lee: Iced Tea, $5.99
How to determine how much each friends paidFrom clue 1, we know that either Calvin or the person who got the Root Beer paid $4.99. Since Calvin paid more than Lee according to clue 4, Calvin cannot be the one who got the Root Beer. Therefore, Calvin paid $4.99.
From clue 2, Kelli paid $6.99.
From clue 3, the person who got the water paid $1 less than Dean. Since Dean paid the highest price, the person who got the water paid $1 less, which means Lee paid $5.99.
From clue 5, the person who got the Root Beer paid $1 less than the person who got the Iced Tea. Since Calvin got the Root Beer, Lee must have gotten the Iced Tea.
Therefore, the final assignments are:
Calvin: Root Beer, $4.99
Dean: Lemonade, $7.99
Kelli: Water, $6.99
Lee: Iced Tea, $5.99
Learn more about word problems at https://brainly.com/question/21405634
#SPJ1
the product of "-1.8" and 3 more than a number as the same as 1 / 10 what is the number
Answers
The product of -1.8 and = -1.8 x ?
3 more than a number = 3 + n
The product of -1.8 and 3 more than a number = -1.8(3 + n)
Is the same as 1/10 = equals (equal sign) 1/10
Full Equation: -1.8(3 + n) = 1/10
Steps to solve:
1. Divide both sides by -1.8 (or - 9/5)
(3 + n) = 1/10 x -5/9
3 + n = -5/90
2. Subtract 3 from both sides
n = -5/90 - 270/90
n = -30 5/9
Hope this helps!
What is the total surface area??

Answers
Check the picture below.
\(\stackrel{\textit{\LARGE Areas}}{ \stackrel{\textit{two triangles}}{2\left[\cfrac{1}{2}(\underset{b}{8})(\underset{h}{6}) \right]}~~ + ~~\stackrel{\textit{three rectangles}}{(14)(6)~~ + ~~(14)(8)~~ + ~~(14)(10)}} \\\\\\ 48~~ + ~~84~~ + ~~112~~ + ~~140\implies \text{\LARGE 384}~cm^2\)

what is the long method of 23 ÷ 650
Answers
Answer: The long division method is a way to solve division problems by hand. Here are the steps to do long division:
Write the dividend (the number being divided) inside a long division bracket, and write the divisor (the number doing the dividing) outside of the bracket.
Divide the first digit of the dividend by the divisor. Write the answer (the quotient) above the dividend, and write any remainder (what’s left over) below the first digit of the dividend.
Bring down the next digit of the dividend next to the remainder.
Repeat step 2 until you’ve brought down all of the digits of the dividend.
The final answer is your quotient with any remainder written as a fraction.
Angle FGH is a straight angle.
The measure of angle FGJ is 85°.
The measure of angle JGHISO
What is the value of x?
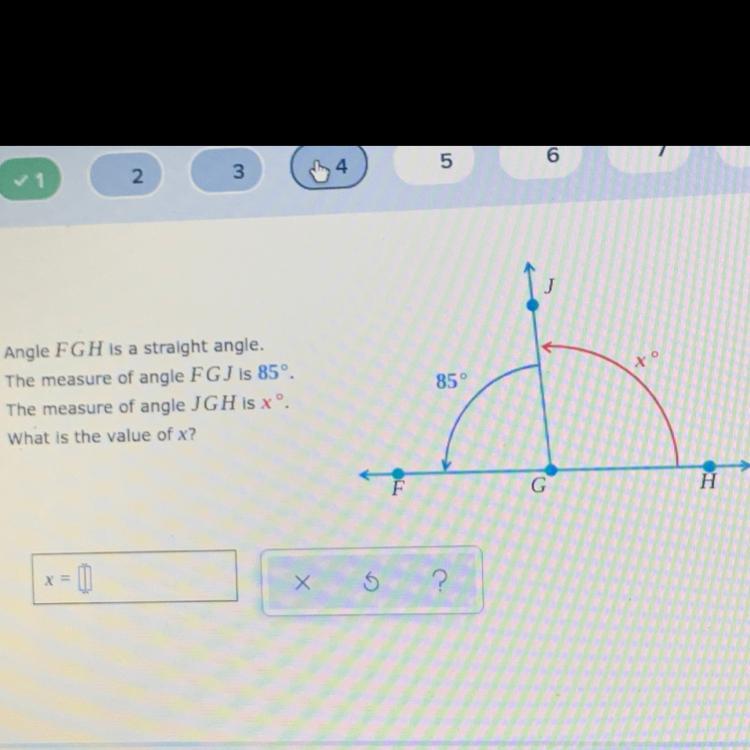
Answers
Answer:
x = 95
Step-by-step explanation:
angles that form a straight line add up to equal 180
Thus, x + 85 = 180
180 - 85 = 95
Hence, x = 95
A family eats at a restaurant. The bill, including tax, is $45. The family then leaves a 20% tip. How much did the family spend on the meal? *
Answers
Answer:
$54
Step-by-step explanation:
45 increase 20% =
45 × (1 + 20%) = 45 × (1 + 0.2) = 54
Which equation is represented by the model? 3x2 – 4x – 1 = (3x 1)(x – 1) 3x2 – 2x – 1 = (3x – 1)(x 1) 3x2 – 4x 1 = (3x – 1)(x – 1) 3x2 – 2x 1 = (3x – 1)(x – 1)
Answers
The equation represented by the model is 3x²-4x+1=(3x-1)(x-1).
Given model represents a polynomial of the form ax²+bx and model is in figure.
Consider the given table.
The first row in the table represents first term of the polynomial.
In first row first three terms are variables and last term are constant.
Write all the terms of the first row in the form of sum.
+x+x+x-1=3x-1
The first column in the table represents second term of the polynomial.
In first column first term are variable and last term are constant.
Write all the terms of the first column in the form of sum.
+x-1=x-1
The product of first term of polynomial (3x-1) and second term of polynomial (x-1) is equal to the sum of all remaining terms in this table.
+x²+x²+x²-x-x-x-x+1=3x²-4x+1.
We can also check this by multiplying (3x-1) and (x-1) as
(3x-1)(x-1)=3x(x-1)-1(x-1)
(3x-1)(x-1)=3x(x)-3x(1)-1(x)+1(1)
(3x-1)(x-1)=3x²-3x-x+1
(3x-1)(x-1)=3x²-4x+1
Hence, the equation represented by the given model in the form of polynomial ax²+bx is (3x-1)(x-1)=3x²-4x+1.
Learn more about equations from here brainly.com/question/12123823
#SPJ4

The circle below is centered at the origin and has a radius of 5. What is its
equation?
A. x2 - y2= 5
B. x2 + y2 = 25
c. x2 + y2 = 5
D. x2 - y2 = 25

Answers
Answer:
Option B is the correct answer
Step-by-step explanation:
B. x2 + y2 = 25
how many minors does it take to catch a case
A) 1
B) 3
C) 69
Answers
PLEASE I BEGGGGG IN A RUSH
The circle with the equation
(x-1)^2 + (y-k)^2 =50 passes through the point (2,3)
find the possible values for k
Answers
The possible values of k for the equation of circle are -4 and 7.
What is a circle?A circle is a two-dimensional figure with a radius and circumference of 2πr.
The area of a circle is πr².
We have,
The equation of a circle is (x - 1)² + (y - k)² = 50
The equation of the circle passes through the point (2, 3) = (x, y).
Now,
(2 - 1)² + (3 - k)² = 50
1 + (3 - k)² = 50
(3 - k)² = 50 - 1
3 - k = √49
3 - k = ±7
Now,
3 - k = 7
3 - 7 = k
k = -4
3 - k = -7
3 + 7 = k
k = 10
Thus,
The possible values of k are -4 and 10.
Learn more about circle here:
https://brainly.com/question/11833983
#SPJ1
what is the probability that a positive integer not exceeding 100 selected at random is divisible by 5 or 7
Answers
Answer:
So, the probability of selecting a number from 1 to 100 that is divisible by 5 or 7 is 0.32.
Hope this helped!
What is the answer to The sum of 2 numbers is 19 and their difference is 3? And thank you brainly for helping. I need the answers correct because I play prodigy, a math game. Thank you!
Answers
Answer:
11 and 8
Step-by-step explanation:
11+8=19
11-8=3
Answer:
8 and 11
Step-by-step explanation:
We want to compare two brake lights in terms of reaction times by drivers. We run an experiment in which a random sample of drivers is tested on both lights (each driver is tested on both lights), and we find that 60% of drivers in the sample react quicker to the new light as compared to the old. Which of the following could be the correct 95% confidence interval for the proportion of drivers who react more quickly to the new light? (Note, there is only one possible correct answer here, and you should not be actually calculating the CI).
answer : (0.53,0.67)
show how to get answer
Answers
The correct 95% confidence interval for the proportion of drivers who react more quickly to the new light is (0.53, 0.67).
To calculate the confidence interval for the proportion of drivers who react more quickly to the new light, we can use the formula:
CI = p ± zα/2 √((p(1-p))/n)
where p is the proportion of drivers who react more quickly to the new light, n is the sample size, and zα/2 is the z-score for the desired confidence level (in this case, 95% corresponds to zα/2 = 1.96).
Substituting the given values, we get:
CI = 0.6 ± 1.96 √((0.6*0.4)/n)
Since we don't know the sample size, we can't calculate the exact confidence interval. However, we can see that the margin of error is proportional to 1/√n, which means that larger sample sizes will result in narrower confidence intervals.
Based on the given answer choices, we can see that the margin of error is 0.07, which corresponds to a sample size of around 200. So, if we assume that the sample size is large enough to use the normal approximation, we can calculate the confidence interval as:
CI = 0.6 ± 0.07
which gives us (0.53, 0.67) as the correct answer.
For more questions like Sample click the link below:
https://brainly.com/question/31101410
#SPJ11
The forecast for 2019 by the linear regression method is 87.3723 83.7387 89.0824 84.9406
forecasting regression File Edit View Insert Format Tools Data Window T ABC ABC B Calibri 11 fx Σ = A C E ***
Answers
The linear regression method forecasts the values for 2019 as 87.3723, 83.7387, 89.0824, and 84.9406.
To provide a step-by-step explanation of the linear regression method used to forecast the values for 2019:
Linear regression is a statistical technique used to model the relationship between a dependent variable and one or more independent variables. In this case, the dependent variable is the forecasted value for 2019, and the independent variable is time.
The given forecast values, 87.3723, 83.7387, 89.0824, and 84.9406, represent the predicted values for the corresponding time periods.
The linear regression method estimates a straight line that best fits the historical data, allowing for the prediction of future values. In this case, the method estimates the relationship between time and the forecasted values.
By fitting a linear regression model to the historical data, the method calculates the coefficients for the line equation, which represents the trend or pattern observed in the data.
Once the coefficients are determined, the linear regression model can be used to forecast values for future time periods. The model assumes that the relationship between time and the forecasted values will continue to follow the estimated trend.
In this case, the linear regression method predicts the values 87.3723, 83.7387, 89.0824, and 84.9406 for the year 2019 based on the observed trend in the historical data.
It's important to note that without additional context or information about the specific dataset and variables involved, it's difficult to provide a more detailed explanation. The linear regression method relies on the assumption that the relationship between the dependent and independent variables is linear and that there are no other significant factors influencing the forecasted values.
For more questions like Linear regression click the link below:
https://brainly.com/question/32505018
#SPJ11
Are these numbers linear or nonlinear?
x: 0, 1, 2, and 3
y: 1, 3, 6, and 10,
What about this one?
x: 0, 3, 6, and 9
y: -3, 9, 21, and 33
Answers
Answer:
The first one is non-linear.
The second is linear.
help me plzzzzzzzzzzzzzzzzzzzzz

Answers
Answer:
A and B
Step-by-step explanation:
96% of 25
= \(\frac{96}{100}\) × 25 ( per cent means out of 100 ) → A
= 0.96 × 25 ( divide 96 by 100 ) → B
Find the limit. Use l'Hospital's Rule if appropriate. If there is a more elementary method, consider using it.
lim (x + x²)/(2 − 3x²)
x→[infinity]
Answers
The limit of (x + x²)/(2 − 3x²) as x approaches infinity is -1/3.
To find the limit of (x + x²)/(2 − 3x²) as x approaches infinity, we can use l'Hospital's Rule.
First, we need to check if the limit is in the indeterminate form 0/0 or ∞/∞. As x approaches infinity, both the numerator (x + x²) and the denominator (2 - 3x²) approach infinity.
Therefore, the limit is in the indeterminate form ∞/∞, and we can apply l'Hospital's Rule.
l'Hospital's Rule states that if the limit is in the indeterminate form 0/0 or ∞/∞, we can take the derivative of the numerator and denominator separately, and then find the limit of the ratio of their derivatives.
Numerator's derivative: d/dx(x + x²) = 1 + 2x Denominator's derivative: d/dx(2 - 3x²) = -6x
Now, we'll find the limit of the ratio of their derivatives as x approaches infinity: lim (1 + 2x)/(-6x) as x→∞
We can use l'Hospital's Rule again, as this limit is also in the indeterminate form ∞/∞. Numerator's second derivative: d/dx(1 + 2x) = 2
Denominator's second derivative: d/dx(-6x) = -6
Now, we'll find the limit of the ratio of their second derivatives as x approaches infinity: lim (2)/(-6) as x→∞ Since the limit involves constants only, it does not depend on x, and we can directly compute the limit: 2 / (-6) = -1/3
Therefore, the limit of (x + x²)/(2 − 3x²) as x approaches infinity is -1/3.
Learn more about l'Hospital's Rule,
https://brainly.com/question/28170672
#SPJ11
help me with this question please

Answers
Answer:
N+1
Step-by-step explanation:
It begins with = 2
then n+1=3
then n+2=4 and so on it is n+1
For some tasks, a sigmoid learning curve is used to model proficiency. Suppose the percent proficiency is given by the model P(t)=100/1+40e^0.3t, where t is days of practice. Find the inflection point, the point where additional practice starts producing diminishing returns. Give your answer accurate to at least 2 decimal places. Comment
Answers
The inflection point occurs at approximately 17.34 days of practice, where the proficiency growth rate starts to decrease.
The inflection point of the sigmoid curve happens when the pace of expansion in capability begins to diminish. This is the point at which the second derivative of the curve equals zero.
To find the inflection point of the curve P(t) = 100/(1 + 40e^(0.3t)), we want to track down the second derivative of P(t) with respect to t:
P(t) = 100/(1 + 40\(e^{(0.3t)}\))
P'(t) = (- 1200\(e^{(0.3t)}\))/(1 + 40\(e^{(0.3t)}\))²
P''(t) = (10800\(e^{(0.6t)}\))/(1 + 40\(e^{(0.3t)}\))³ - (3600\(e^{(0.3t)}\))/(1 + 40\(e^{(0.3t)}\))^2
Setting P''(t) equivalent to nothing and addressing for t, we get:
(10800\(e^{(0.6t)}\))/(1 + 40\(e^{(0.3t)}\))³ - (3600\(e^{(0.3t)}\))/(1 + 40\(e^{(0.3t)}\))² = 0
Working on this articulation by duplicating the two sides by (1 + 40\(e^{(0.3t)}\))³, we get:
10800\(e^{(0.6t)}\) - 3600\(e^{(0.3t)}\)(1 + 40\(e^{(0.3t)}\)) = 0
Partitioning the two sides by 3600\(e^{(0.3t)}\), we get:
3\(e^{(0.3t)}\) - (1 + 40\(e^{(0.3t)}\)) = 0
Expanding and simplifying this expression, we get:
3\(e^{(0.3t)}\) - 1 - 40\(e^{(0.3t)}\) = 0
39\(e^{(0.3t)}\) = 1
\(e^{(0.3t)}\) = 1/39
Taking the natural logarithm of both sides, we get:
0.3t = ln(1/39)
t = (ln(1/39))/0.3
t ≈ 17.34 days
As a result, the proficiency development rate starts to slow down after about 17.34 days of practice, which is the inflection point.
Learn more about inflection points at
https://brainly.com/question/30760634
#SPJ4
Find the unknown sizes of angles in the following figure (please explain it):

Answers
Answer:
x = 56
MKL = 56
KML= 63
MLK = 61
Step-by-step explanation:
We know that the sum of the interior angles of a triangle = 180 degrees.
So, x+ (x+7)+ ( x+5) = 180
3x+ 12= 180
3x= 180-12 = 168
168/3 = x
therefore, x= 56 degrees.
So MKL = 56
KML= 56+ 7 = 63
MLK = 56+5 = 61
In ratio a:b, the first term a is called
O antecedent
O extreme
O consequent
mean
Pls someone help me
Answers
Question 6 (4 points) Three people use the following procedure to divide a (perfectly divisible and homogenous) cake. Player 1 first divides the cake into two pieces. Next, player 2 selects one of the two pieces. Player 1 gets the other share, while player 2 must now divide the piece he or she picked. Finally, player 3 chooses one of the two pieces that player 2 just created, and player 2 consumes what remains. Suppose that each player cares only about the size of the piece of cake he or she ultimately obtains. Compute the subgame perfect Nash equilibrium (please provide complete strategies, not just the equilibrium payoffs).
Answers
The subgame perfect Nash equilibrium involves Player 1 receiving a piece that is no less than 1/4 of the original cake, Player 2 receiving a piece that is no less than 1/2 of the cake, and Player 3 receiving a piece that is no less than 1/4 of the cake. Player 2 obtains the largest piece at 1/2 of the cake, while Player 1 gets a share that is no less than 1/4 of the cake, which is larger than Player 3's share of the remaining cake.
The subgame perfect Nash equilibrium and complete strategies are as follows:
First subgame: Player 1 splits the cake into two pieces. Player 1 takes the smaller of the two pieces, while Player 2 takes the larger. Next, Player 2 divides the larger piece into two. Player 2 chooses the piece that is equal in size to the smaller piece of the initial division. Player 2 gives the other piece to Player 3, who must now select one of the two pieces. If Player 3 selects the smaller piece, Player 2 will obtain the larger of the two pieces that Player 2 divided, which is greater than or equal in size to the piece Player 2 gave to Player 3. As a result, Player 3 chooses the larger of the two pieces. Therefore, the subgame perfect Nash equilibrium involves Player 1 receiving a piece that is no less than 1/4 of the original cake, Player 2 receiving a piece that is no less than 1/2 of the cake, and Player 3 receiving a piece that is no less than 1/4 of the cake. Player 2 obtains the largest piece at 1/2 of the cake, while Player 1 gets a share that is no less than 1/4 of the cake, which is larger than Player 3's share of the remaining cake.Learn more about Nash equilibrium:
brainly.com/question/29398344
#SPJ11
What are the x-intercepts of the quadratic function? parabola going down from the left and passing through the point negative 2 comma 0 then going to a minimum and then going up to the right through the points 0 comma negative 2 and 1 comma 0 a (0, −2) and (0, 1) b (0, −2) and (0, 2) c (−2, 0) and (2, 0) d (−2, 0) and (1, 0)
Answers
The x-intercepts of a quadratic function are the points where the function graph intersects the x-axis. To find the x-intercepts of the given quadratic function, we need to determine the values of x when the y-value (or the function value) is equal to 0.
From the given information, we can see that the quadratic function passes through the points (-2, 0) and (1, 0), which indicates that the function intersects the x-axis at x = -2 and x = 1. Therefore, the quadratic function x-intercepts are (-2, 0) and (1, 0).
The correct answers are (d) (-2, 0) and (1, 0).
HELP ME!!! I WILL GIVE BRAINLIEST AND 15 POINTS!!!!!!!!
Evaluate each expression for n = 3, p = 10.5, t = -2, y = 4.
Solve
1.) 3n + 2t
2.) ny - 6 + p
Answers
9-4
5
2) (3)(4)-6+10.5
12-6+10.5
6+10.5
16.5
Therefore, the solution to #1 is 5, and the solution to #2 is 16.5.
2. 16.5
Plug in the values and solve.
LESSON 12 SESSION 1
3 Tameka pilots a hot air balloon. She lowers the balloon
five times, going down an equal distance each time. In
all, Tameka lowers the balloon 75 m.
a. What integer represents the change in the hot air
balloon's elevation each time Tameka lowers it?
What does this integer tell you? Show your work.
75/5=-15
Answers
The integer that represents the change in the hot air balloon's elevation each time Tameka lowers it is -15.
To calculate the change in elevation, we can divide the total change in elevation (75 m) by the number of times the balloon is lowered (5).
75 m / 5 = -15
The negative sign indicates that the balloon is being lowered, and the number 15 represents the distance in meters by which the balloon is descending each time it is lowered.
Let's break down the calculation further to understand why this integer represents the change in elevation.
Tameka lowers the balloon five times, and the total change in elevation is 75 meters. Since the balloon is lowered an equal distance each time, we can divide the total change by the number of times lowered to find the change in elevation per lowering.
75 meters / 5 = 15 meters
However, since the balloon is being lowered, the change in elevation is negative. This means that for each lowering, the balloon descends 15 meters downward.
Hence, the integer -15 represents the change in the hot air balloon's elevation each time Tameka lowers it. It tells us that the balloon is being lowered by 15 meters during each lowering, resulting in a total descent of 75 meters when repeated five times.
Learn more about integer here
https://brainly.com/question/31048829
#SPJ11
Help explain how to solve

Answers
The value of the angle U in the triangle is 92.10 degrees.
How to find the angle in a triangle?The angle U in the triangle can be found using cosine rule as follows:
Let's use cosine formula to find the angle U
c² = a² + b² - 2ab cos C
Hence,
Therefore,
a = 58.8
b = 38.4
c = 71.4
Hence,
71.4² = 58.8² + 38.4² - 2(58.8)(38.4) cos U
5097.96 = 3457.44 + 1474.56 - 4515.84 cos U
5097.96 - 4932 = - 4515.84 cos U
165.96 = - 4515.84 cos U
divide both sides by - 4515.84
cos U = 165.96 / - 4515.84
cos U = - 0.03675063775
U = cos⁻¹ - 0.03675063775
U = 92.1032274244
Therefore,
U = 92.10 degrees
learn more on triangle here: https://brainly.com/question/28855901
#SPJ1
Please help I need this done ASAP

Answers
Answer:
Domain is all x values
Range is all y values
Step-by-step explanation:
Your image is not clear enough for me to see the x or y coordinates so hope that helps you to figure it out on your own
sin(20) = cos(2u) = tan(24) = 3. [-/5 Points] Use the given conditions to find the exact values of sin(2u), cos(2u), and tan(2u) using the double-angle formulas. sin(u) = -3/5, 3m/2
Answers
Using the given conditions that sin(20) = cos(2u) = tan(24) = 3, we can find the exact values of sin(2u), cos(2u), and tan(2u) using the double-angle formulas. By substituting the known values into the formulas, we can determine the exact values of these trigonometric functions.
Given sin(20) = 3, we can use the double-angle formula for sine to find sin(2u).
The double-angle formula for sine is sin(2u) = 2sin(u)cos(u). We know that sin(u) = -3/5, so we can substitute this value into the formula to calculate sin(2u).
Therefore, sin(2u) = 2(-3/5)(cos(u)).
Given cos(2u) = 3, we can use the double-angle formula for cosine to find cos(2u).
The double-angle formula for cosine is cos(2u) = cos^2(u) - sin^2(u). Since we already know sin(u) = -3/5 and cos(u) can be calculated using the Pythagorean identity (cos^2(u) = 1 - sin^2(u)), we can substitute these values into the formula to determine cos(2u).
Finally, given tan(24) = 3, we can use the double-angle formula for tangent to find tan(2u).
The double-angle formula for tangent is tan(2u) = (2tan(u))/(1 - tan^2(u)). By substituting the known value of tan(24) = 3 into the formula, we can calculate the exact value of tan(2u).
To learn more about trigonometric functions visit:
brainly.com/question/25618616
#SPJ11
15 first-year algebra students are learning how to solve two-step equations. the teacher notices that the students are not using precise mathematical language. which two instructional strategies should the teacher employ to encourage students to use precise mathematical language when completing this task? choose 2 answers
Answers
Solving an equation in algebra - mathematics will BOMDAS rule. Multiplication, division, addition, and subtraction are performed before.
However, in order to simplify things, if there are any exponential or logarithmic components, solve them first before applying BOMDAS to reduce them to a single solvable term. This is required by the rules.
So the list goes as
1. Exponents
2. Roots
3. Multiplication
4. Division
5. additional
6. Subtraction
However. Using a regular or scientific calculator will generate a lot of debate. A scientific calculator will adhere to the principles, while a typical calculator will evaluate from left to right or precisely the operator used first.
Using a scientific calculator, 5+2x3=11 instead of the normal one's 5+2x3=21.
Furthermore, the preferred behavior norm for division and multiplication is different.
Thus, people's difficulty with mathematics is not unjustified. The choice of how you want to approach it is ultimately up to you.
Know more about algebra
https://brainly.com/question/22399890
#SPJ4