i rlly need some help please if ur big brains im going to be asking multiple questions right now
*BRAINLIEST IF U HELP ME RN*
Answers
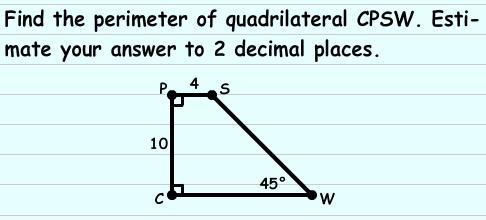
You can break the shape up into a rectangle and a right triangle.
Use your trig ratios to find the missing sides.
Add all the sides up and you have your perimeter!
//
\(p = 2(l) + 2(w)\)
\(p = 2(10) + 2(4)\)
\(p = 28\)
//
\(tan = \frac{opp}{adj} \)
\( \tan(45) = \frac{10}{adj} \)
\(adj = \frac{10}{ \tan(45) } \)
\(adj = 10\)
\( {a}^{2} + {b}^{2} = {c}^{2} \)
\( {10}^{2} + 10 {}^{2} = {200}^{2} \)
\( \sqrt{200} = 14.14213562\)
//
\(p = 10 + 4 + (4 + 10) + 14.14213562\)
*notice how one of the 10 is left out because it is inside the shape so we can't use that to find perimeter.
\(p = 42.14\)

Related Questions
What is the value of x in the diagram below?

Answers
Answer:
57
Step-by-step explanation:
the whole angle is 90
So 90 minus 33 is 57
Integrate by hand the following functions: adr b) (42³-2r+7) dz Upload Choose a File
Answers
The integral of (42³ - 2r + 7) dz is equal to (42³ - 2r + 7)z + C.
To integrate the function (42³ - 2r + 7) dz, we treat r as a constant and integrate with respect to z. The integral of a constant with respect to z is simply the constant multiplied by z:
∫ (42³ - 2r + 7) dz = (42³ - 2r + 7)z + C
where C is the constant of integration.
Note: The integral of a constant term (such as 7) with respect to any variable is simply the constant multiplied by the variable. In this case, the variable is z.
Know more about integration here:
https://brainly.com/question/31744185
#SPJ11
Find the LENGTH OF THE MISSING SIDE in the following right triangle in inches.
Round to the nearest tenth, if necessary.
20 inches
21 inches
Answers
Answer:
If the missing side is long then it's 29 or if its short, then it's 6.4
Step-by-step explanation:
just do a^2 + b^2 = c^2 method
Say whether the given function has limit at the point (0,0). If the limit exists, then find it. (a) f(x, y) = 5ry² 3x² + y² (Hint: the parabola z = - y²); (b) f2(x, y) = Vel+V sin(y). (Hint: [√x + √] × [√ √U] ...). [2,3]
Answers
(a) The function f(x, y) does not have a limit at (0,0). (b) No information is provided to determine the limit for f2(x, y).
(a) For the function f(x, y) = 5ry²/(3x² + y²), we can analyze the behavior as (x, y) approaches (0,0). Since the denominator 3x² + y² becomes zero as (x, y) approaches (0,0), we cannot directly evaluate the function at this point. However, by considering the parabola z = -y², we can observe that the function does not approach a specific value and thus does not have a limit at (0,0).
(b) The function f2(x, y) = Vel + Vsin(y) is not well-defined as no information or context is provided for the variables Vel, V, and U. Without this information, it is not possible to determine the limit of the function at (0,0) or any other point.
Therefore, for (a), the function f(x, y) does not have a limit at (0,0), and for (b), no information is given to determine the limit for f2(x, y).
To learn more about “variable” refer to the https://brainly.com/question/28248724
#SPJ11
Evaluate the expression. Use y = -6.
y? – 4y + 8
Answers
Answer:
-6-4(-6)+8
-6+24+8
-6+32
26
Answer:
y=7
Step-by-step explaynation:
Use the Chain Rule to evaluate the partial derivative
∂θ
∂g
at the point (r,θ)=(2
2
,
4
π
) where g(x,y)=
8x+9y
2
1
,x=rsinθ,y=rcosθ.
∂θ
∂g
∣
∣
(r,θ)=(2
2
,
4
π
)
=
Answers
\(The given function is `g(x,y) = 8x + 9y^(1/2)`.\) To find `∂θ/∂g`, we need to use the chain rule.
\(We are given that `x = r sinθ` and `y = r cosθ`. Therefore, `g(r,θ) = 8r sinθ + 9(r cosθ)^(1/2)`.\)
Here's the solution:
\(Now, we will find `∂g/∂θ` and `∂g/∂r` first:∂g/∂θ = 8r cosθ - `(9/2)r^(-1/2)sinθ`∂g/∂r = 8sinθ + `(9/2)r^(-1/2)cosθ`\)
\(Now, we can find `∂θ/∂g` by using the formula:`∂θ/∂g` = `(∂g/∂θ) / (∂g/∂r)`\)
\(Therefore,`∂θ/∂g` = `(8r cosθ - (9/2)r^(-1/2)sinθ) / (8sinθ + (9/2)r^(-1/2)cosθ)`\)
\(Now, we can substitute the given values `(r,θ) = (2, 4π)` into the expression for `∂θ/∂g`:`∂θ/∂g ∣∣ (r,θ) = (2, 4π)`=`(8(2)(-1) - (9/2)(2)^(-1/2)(0)) / (8(0) + (9/2)(2)^(-1/2)(-1))`=`(-8)/(9/2sqrt(2))`=`-8sqrt(2)/9`\)
\(Therefore, `∂θ/∂g ∣∣ (r,θ) = (2, 4π)`=`-8sqrt(2)/9`.\)
Hence, the required partial derivative is `-8sqrt(2)/9`.
To know more about the word formula visits :
https://brainly.com/question/30333793
#SPJ11
a-If given that we were tasked to evaluate the model, between MAPE and R2 which of these parameters do we use?
b-If given that model A has a higher MAPE than model B but model B has a higher R2 than model A, then how do we choose among the two?
c-Between the MAPE , MAD and MSD, which of these parameters shall we use for accuracy measures and why?
Answers
a. When evaluating a model, we use R2 as a parameter for performance assessment.
b. If model A has a higher MAPE but model B has a higher R2, we choose the model with the higher R2 for better overall performance.
c. For accuracy measures, we typically use MAPE (Mean Absolute Percentage Error) due to its interpretability and ability to capture relative errors.
When evaluating a model's performance, it is crucial to choose the appropriate parameters to assess its accuracy and reliability. In the case of MAPE (Mean Absolute Percentage Error) and R2 (Coefficient of Determination), the choice between them depends on the specific evaluation goals.
The R2 parameter is commonly used for evaluating models because it measures the proportion of the dependent variable's variance that can be explained by the independent variables. R2 provides insights into how well the model fits the data and captures the relationship between the input features and the target variable. Therefore, R2 is a suitable parameter to use when evaluating a model.
When comparing two models, if model A has a higher MAPE but model B has a higher R2, it is advisable to choose the model with the higher R2 value. This is because R2 indicates the proportion of variance explained, suggesting that model B performs better in capturing the underlying patterns and predicting the target variable.
Although model A may have a lower relative error (MAPE), it is crucial to prioritize the model's ability to explain and predict the target variable accurately.
Among MAPE, MAD (Mean Absolute Deviation), and MSD (Mean Squared Deviation), MAPE is commonly preferred as a parameter for accuracy measures. MAPE calculates the average percentage difference between the predicted and actual values, making it interpretable and easily understandable.
It captures relative errors and enables comparisons across different scales and datasets. MAD and MSD, on the other hand, measure absolute and squared errors, respectively, but they do not account for the relative magnitude of the errors. Hence, MAPE is a more suitable parameter for accuracy measures.
Learn more about Model
brainly.com/question/32196451
#SPJ11
HELP I WILL MARK BRAINLIST

Answers
what is the critical value for 96 confidence interval for a sample size of 15
Answers
The critical t-value is approximately 1.753.
To find the critical value for a 96% confidence interval with a sample size of 15, we need to determine the t-value from the t-distribution table. The t-distribution table is a statistical tool used to determine the probability of a t-value given the degrees of freedom (df) and the desired level of significance (α).
In this case, we have a sample size of 15, which means our degrees of freedom are 14 (n - 1). Looking at a t-distribution table for 14 degrees of freedom and a 96% confidence interval.
This means that if we were to construct a confidence interval from a sample size of 15, the margin of error would be calculated by multiplying the critical t-value of 1.753 by the standard deviation of the sample and dividing by the square root of the sample size. The resulting interval would contain the population mean with 96% confidence.
It's essential to note that the critical value will change as the sample size and confidence level change. Therefore, it's crucial to use the correct table to find the corresponding critical values for a given dataset's sample size and confidence level.
For such more questions on critical
https://brainly.com/question/30459381
#SPJ8
find the volume of the largest right circular cylinder (in units^3) that fits in a sphere of radius 4 units.
Answers
The volume of the largest right circular cylinder (in cubic units) that fits in a sphere of radius 4 units is 154.7 cubic units.
First, draw a diagram. The diagram shows the cylinder inscribed in the sphere. Given that in the diagram the height, h, we can find the radius of the cylinder in terms of r using the Pythagorean Theorem.
h represents half of the total height of the cylinder. choose h instead of h² to simplify things better.
To find the volume of the cylinder, we need to multiply the area of the top by the total height of the cylinder. In other words;
V = π(radius of cylinder)²(height of cylinder)
V = π(√r²−h²)²(2h)
V = 2πh(r²−h²)
V = 2π(r²h−h³)
d/dxV(h) = 2π(r²−3h²) = 0
The 2π divides out and we are left with;
r²−3h² = 0
After some rearranging;
h² = r²/3
Take the square root of both sides.
h = r/√3
To find the volume, we need to put this into the volume equation.
V = 2πh(r²−h²) = 2π(r/√3){r²−(r/√3)²}
V = (2πr/√3)(r²−r²/3)
V = (2πr/√3){(3r²−r²)/3}
V = (2πr/√3)(2r²/3)
V = 4πr³/3√3
V = 4√3πr³/9
Now, put the value of r in the above equation, and we get
V = 4√3π(4)³/9
V = 256√3π/9
V = 154.7 cubic units
To know more about volume, here
https://brainly.com/question/13338592
#SPJ4

3. David is a salesman for a local Ford dealership. He is paid a percent of the profit the dealership makes on each
car. If the profit is under $800, the commission is 25%. If the profit is at least $800 and less than $1,000, the
commission rate is 27.5% of the profit. If the profit is $1,000 or more, the rate is 30% of the profit. Find the
difference between the commission paid if David sells a car for a $1,000 profit and the commission paid if he
sells a car for a $799 profit?
.25x,
p(x) = 3.275x,
x < $800
$800 < x < $1000
x $1000
.30x,
Answers
David is a salesman for a local Ford dealership. He is paid a percentage of the profit the dealership makes on each car. If the profit is under $800, the commission is 25%.
If the profit is at least $800 and less than $1,000, the commission rate is 27.5% of the profit. If the profit is $1,000 or more, the rate is 30% of the profit.
Let's find the difference between the commission paid if David sells a car for a $1,000 profit and the commission paid if he sells a car for a $799 profit. We'll begin by finding the commission paid if David sells a car for a $1,000 profit.Commission paid on a $1,000 profit=.30(1,000)=300
Therefore, if David sells a car for a $1,000 profit, his commission is $300. Let's move on to finding the commission paid if he sells a car for a $799 profit. Commission paid on a $799 profit=.25(799)=199.75Therefore, if David sells a car for a $799 profit, his commission is $199.75.The difference between these commissions is:$300-$199.75=$100.25
Therefore, the difference between the commission paid if David sells a car for a $1,000 profit and the commission paid if he sells a car for a $799 profit is $100.25.
To know more about percentage visit:
https://brainly.com/question/32197511
#SPJ11
Which could be the area of one face of the rectangular prism?.
Answers
To begin with, let's first understand what a rectangular prism is. A rectangular prism is a three-dimensional object that has six faces,
Each of which is a rectangle. The faces are parallel and congruent, meaning they have the same size and shape. Now, coming to your question, you are asking about the area of one face of the rectangular prism.
Since all the faces of a rectangular prism are rectangles, the area of one face can be calculated by multiplying the length and width of the face.
For example, if the length of the rectangular prism is 5 units and the width is 3 units, the area of one face would be 5 x 3 = 15 square units. The units used to measure the length and width will also determine the unit of measurement for the area.
So, to summarize, the area of one face of a rectangular prism can be found by multiplying the length and width of that face.
if you have a rectangular prism with dimensions of length = 5 units, width = 4 units, and height = 3 units, you can calculate the area of each face as follows:
1. Length x width: 5 x 4 = 20 square units
2. Length x height: 5 x 3 = 15 square units
3. Width x height: 4 x 3 = 12 square units
So, the areas of the three different pairs of faces for this rectangular prism are 20, 15, and 12 square units, respectively.
To know more about length click here
brainly.com/question/30625256
#SPJ11
A=3 and B=5, evaluate the following:
5logA^1/2 + log B
Answers
The value of the expression 5log(A^(1/2)) + log(B) with A = 3 and B = 5 is approximately 1.8929.
To evaluate the expression 5log(A^(1/2)) + log(B) with A = 3 and B = 5, we substitute the given values into the expression:
5log(3^(1/2)) + log(5)
First, let's simplify the term inside the logarithm.
3^(1/2) represents the square root of 3, which is approximately 1.732.
Now we substitute this value back into the expression:
5log(1.732) + log(5)
Using a calculator, we can find that log(1.732) is approximately 0.2388.
Now we substitute this value back into the expression:
5(0.2388) + log(5)
Evaluating the expression further, we find:
1.194 + log(5)
The logarithm of 5 is approximately 0.6989.
Substituting this value into the expression, we have:
1.194 + 0.6989
Adding these values together, we get:
1.8929
Therefore, the value of the expression 5log(A^(1/2)) + log(B) with A = 3 and B = 5 is approximately 1.8929.
Know more about logarithm here:
https://brainly.com/question/30340014
#SPJ8
Debbie's cupcakes recently sold 3 vanilla cupcakes and 3 other cupcakes. what is the experimental probability that the next cupcake sold will be a vanilla cupcake?
Answers
The answer to the experimental probability that a vanilla cupcake will be the next one sold is 0.5, or 50%.
The experimental probability of an event is the ratio of the number of times the event occurs to the total number of trials or experiments. In this case, the event is selling a vanilla cupcake and the total number of cupcakes sold is 6. Since 3 out of the 6 cupcakes sold were vanilla, the experimental probability of the next cupcake sold being vanilla is:
Experimental probability = Number of times event occurred / Total number of trials
Experimental probability = 3/6
Experimental probability = 0.5
Therefore, the experimental probability that the next cupcake sold will be a vanilla cupcake is 0.5 or 50%.
To learn more about probability click here
brainly.com/question/30034780
#SPJ1
An airplane needs to head due north, but there is a wind blowing from the northwest at 60 km/hr. The
plane flies at an airspeed of 800 km/hr
Answers
The plane's genuine speed (ground speed) is around 771.2 km/hr, and its bearing is somewhat toward the east of north.
We must take into account the effect of the wind in order to determine the actual velocity (ground speed) and direction of the airplane.
Given:
The plane's airspeed is 800 km/hr, and the wind speed is 60 km/hr. The wind is blowing in the northwest. First, let's divide the wind into its northward and westward components. Since the breeze is blowing from the northwest, it has both toward the north and toward the west parts.
Trigonometry can be used to calculate the components of the wind. Since the northwest course is 45 degrees among north and west, we can track down the parts as follows:
Wind speed * sin(45°) = 60 km/hr * sin(45°) = 60 km/hr * 2 / 2 = 30 km/hr Wind speed * cos(45°) = 60 km/hr * cos(45°) = 60 km/hr * 2 / 2 = 30 km/hr Now, let's take into account the effects of the wind when calculating the actual velocity (ground speed) and direction of the airplane.
Since the plane requirements to head due north, it should neutralize the toward the west part of the breeze to keep up with its toward the north course.
Genuine speed (ground speed) = Velocity of the plane - Toward the west part of the breeze
= 800 km/hr - 30√2 km/hr
≈ 771.2 km/hr (adjusted to one decimal spot)
The heading of the plane will be somewhat toward the east of north, as it makes up for the toward the west wind part.
Thusly, the plane's genuine speed (ground speed) is around 771.2 km/hr, and its bearing is somewhat toward the east of north.
To know more about Velocity refer to
https://brainly.com/question/18084516
#SPJ11
Develop an essenential smoothing forecast (α=0.45) for penods 11 through 15 Assume that your forecast for penod 10 was 297 Calculate the forecasts for perieds 11 through 15 (enter your responses rocmdod to tivo decimal places)
Answers
The forecasts for periods 11 through 15 are: F11 = 297.4, F12 = 296.7, F13 = 297.1, F14 = 296.9, F15 = 297.0
Given: Smoothing constant α = 0.45, Forecast for period 10 = 297
We need to calculate the forecasts for periods 11 through 15 using the essential smoothing forecast method.
The essential smoothing forecast is given by:Ft+1 = αAt + (1 - α)
Ft
Where,
At is the actual value for period t, and Ft is the forecasted value for period t.
We have the forecast for period 10, so we can start by calculating the forecast for period 11:F11 = 0.45(297) + (1 - 0.45)F10 = 162.35 + 0.45F10
F11 = 162.35 + 0.45(297) = 297.4
For period 12:F12 = 0.45(At) + (1 - 0.45)F11F12 = 0.45(297.4) + 0.55(297) = 296.7
For period 13:F13 = 0.45(At) + (1 - 0.45)F12F13 = 0.45(296.7) + 0.55(297.4) = 297.1
For period 14:F14 = 0.45(At) + (1 - 0.45)F13F14 = 0.45(297.1) + 0.55(296.7) = 296.9
For period 15:F15 = 0.45(At) + (1 - 0.45)F14F15 = 0.45(296.9) + 0.55(297.1) = 297.0
Therefore, the forecasts for periods 11 through 15 are: F11 = 297.4, F12 = 296.7, F13 = 297.1, F14 = 296.9, F15 = 297.0 (All values rounded to two decimal places)
Know more about Smoothing constant:
https://brainly.com/question/32292658
#SPJ11
Math asap!! Will give brainliest

Answers
Step-by-step explanation:
line QS = RS
line KJ = half of line KC
What is the equation written in vertex form of a parabola
with a vertex of (9, -1) that passes through (7, 7)?
Answers
Answer:
y = 2(x - 9)² - 1
Step-by-step explanation:
The equation of a parabola in vertex form is
y = a(x - h)² + k
where (h, k) are the coordinates of the vertex and a is a multiplier
Here (h, k ) = (9, - 1 ) , thus
y = a(x - 9)² - 1
To find a substitute (7, 7 ) into the equation
7 = a(7 - 9)² - 1 ( add 1 to both sides )
8 = 4a ( divide both sides by 4 )
2 = a , then
y = 2(x - 9)² - 1
How do you solve what is 2/3 of 3/4?
Answers
Answer:
0.5
Step-by-step explanation:
\(9z + 6j = 98\)
Answers
Answer:
Step-by-step explanation:
What variable are you solving for?
A box contains 18 tennis balls of which 8 are new (unused). Suppose Serena picks two balls at random, plays with them, then returns them to the box. If Venus then picks three balls from the box at random, what is the probability these three are all new (unused)
Answers
The probability that Venus picks three new (unused) balls from the box is 0.1296.Given that a box contains 18 tennis balls of which 8 are new (unused).
We have to find the probability that these three are all new (unused).We know that the balls Serena played with were then returned to the box, so there are 8 new balls left and a total of 19 tennis balls in the box.
Therefore, the probability of picking a new (unused) ball is `8/19`.
Thus, the probability that Venus picks three new (unused) balls from the box is `P(Three new balls) = P(New ball) × P(New ball) × P(New ball) = (4/9) × (8/19) × (8/19) = 0.1296`.Hence, the probability that Venus picks three new (unused) balls from the box is 0.1296.
Summary:A box contains 18 tennis balls of which 8 are new (unused). The probability that Venus picks three new (unused) balls from the box is `P(Three new balls) = P(New ball) × P(New ball) × P(New ball) = (4/9) × (8/19) × (8/19) = 0.1296`.
Learn more about probability click here:
https://brainly.com/question/13604758
#SPJ11
Can someone help me

Answers
Answer:
40
Step-by-step explanation:
90 + 4x - 8 + 4x + 2 = 180
= 8x = 96
= x = 12
m < a = 4(12)-8 = 40
Write a simplified expression for the perimeter of the rectangle

Answers
Explanation: We know that perimeter is each side added, so take those two expressions and then them twice.
-10t^2-t + -10t^2-t = -20t^2-2t
and
3t^2+5t + 3t^2+5t= 6t^2+10t
then take those 2 resulting expressions and add them.
-20t^2-2t+6t^2+10t
combine like terms
-14t^2+8t
simplify
-2t(7t-4)
hopefully that’s right i may have made a mistake so just overlook it -just in case
explain the Alternate Exterior Angles Theorem
Answers
The Alternate Exterior Angles Theorem states that when a pair of parallel lines is intersected by a transversal, the pairs of alternate exterior angles formed on opposite sides of the transversal are congruent.
If line AB and line CD are parallel, and line EF intersects both lines at points G and H respectively, then the angles formed on opposite sides of line EF and on the exterior of the parallel lines are congruent.
The Alternate Exterior Angles Theorem states that when a pair of parallel lines is intersected by a transversal, the pairs of alternate exterior angles formed on opposite sides of the transversal are congruent.
In symbols, the theorem can be written as:
∠1 ≅ ∠4
where ∠1 and ∠4 are alternate exterior angles.
This theorem is useful in solving problems involving angles and parallel lines, and it is commonly used in geometry proofs.
Learn more about Alternate exterior angles theorem here
brainly.com/question/25564520
#SPJ4
M=2 and containing the point (7,6)
Answers
Answer:
\(the \: equation \: of \: the \: line \: is \to \\ \boxed{ \underline{y = 2x - 8 }}\)
Step-by-step explanation:
\(according \: to \: the \: provided \: info : \\ the \: equation \: of \: the \: line \: is \to \\ y - y_{1} = m(x - x_{1}) \\ y - 6 = 2(x -7) \\ y = 2x - 14 + 6 \\ \underline{y = 2x - 8 }\)
(y - 6) = 2(x-7)
y-6 = 2x-14
2x-y= 14-6
2x-y=8
please help with a. of this math question!!!

Answers
do you think it could be x+y=800
One group (A) contains 390 people. Three-fifths of the people in group A will be selected to win $100 fuel cards. There is another group (B) in a nearby town that will receive the same number of fuel cards, but there are 553 people in that group. What will be the ratio of nonwinners in group A to nonwinners in group B after the selections are made? Express your ratio as a fraction or with a colon.
Answers
The ratio of nonwinners in group A to nonwinners in group B after the selections are made is 156 : 319.
What is the ratio?Ratio expresses the relationship between two or more numbers. It shows the frequency of the number of times that one value is contained within other value(s).
Nonwinners in group A = (1 - 3/5) x 390 = 156
Winners in group B = (390 - 156) = 234
nonwinners in group B = 553 - 234 = 319
The ratio = 156 : 319
To learn more about ratios, please check: https://brainly.com/question/25927869
#SPJ1
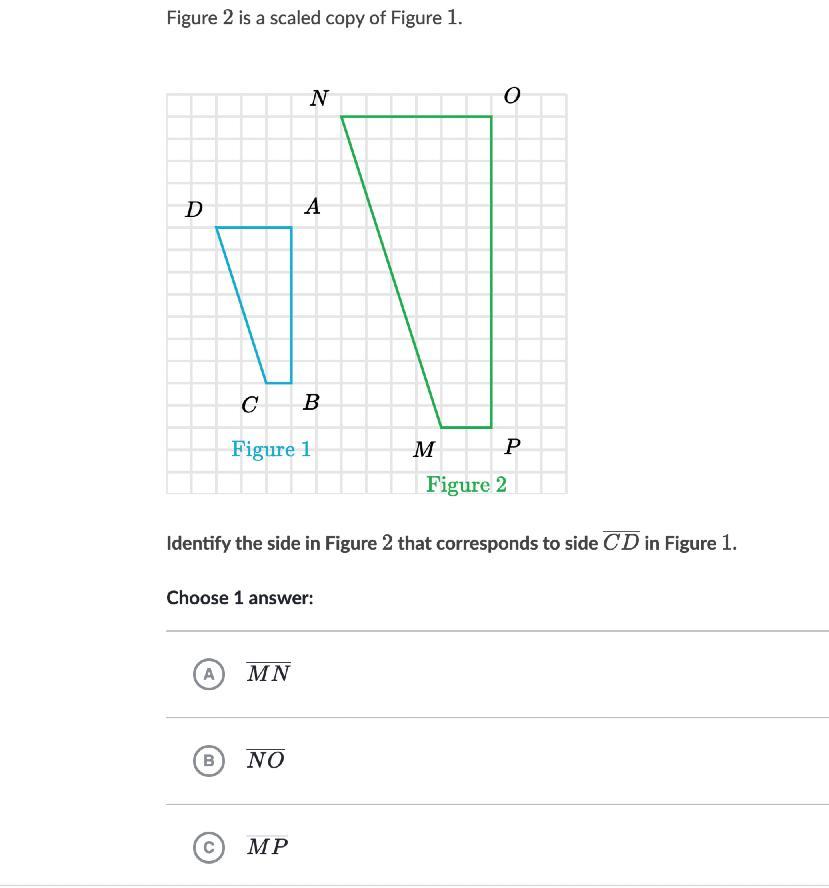
Figure 222 is a scaled copy of Figure 111.
PLEASE HELP
Identify the side in Figure 222 that corresponds to side \overline{CD}
CD
start overline, C, D, end overline in Figure 111.
Choose 1 answer:
Choose 1 answer:
Answers
Convert log_8 1=0 into an exponential equation
o 1^0=8
O 0^8=1
o '8^0=1
o '8^=8
Answers
Given:
The logarithmic equation is:
\(\log_81=0\)
To find:
The exponential equation for the given logarithmic equation.
Solution:
We have,
\(\log_81=0\)
It can be rewritten as:
\(8^{\log_81}=8^{0}\)
Using \(a^{\log_ax}=x\), we get
\(1=8^0\)
\(8^0=1\)
Therefore, the correct option is C.
Easy but not for me. Help needed

Answers
exponent 7 stays same
Answer:
72^7