Answers
\(\tt Step-by-step~explanation:\)
Since we have to write an expression, it will not have an equal sign.
\(\tt Steps:\)
LM is 3x + 5 and LN is 6x + 10. We can assume that M is the midpoint of LN because if you plug in several numbers for x (I'll do 0 and 1), we can see that LM is half the value of LN.
\(\tt 3(0)+5=5\\6(0)+10=10\\5~is~half~of~10,~so~that~means~MN~is~congruent~to~LM.\)
\(\tt 3(1)+5=8\\6(1)+10=16\\8~is~half~of~16,~so~that~means~MN~is~congruent~to~LM.\)
*
\(\large\boxed{\tt Our~final~answer:~MN=3x+5}\)
*Congruent = Same shape and size
Related Questions
Of the approximately 41.3 million of the foreign-born population currently living in the United States, how many are considered unauthorized immigrants
Answers
According to data from the Pew Research Center, there were approximately 10.5 million unauthorized immigrants living in the United States in 2017. This number represents around 25% of the total foreign-born population in the country. In conclusion, out of the 41.3 million foreign-born individuals in the U.S., about 10.5 million are considered unauthorized immigrants.
Unauthorized immigrants, also known as undocumented immigrants, are individuals who enter the United States without legal permission or overstay their visas. They are not eligible for most government benefits and are often subject to deportation if caught.
The Pew Research Center estimates that there were 41.3 million foreign-born individuals living in the United States in 2017, which includes both authorized and unauthorized immigrants. Of this population, around 10.5 million were unauthorized immigrants.
Unauthorized immigration is a complex and contentious issue in the United States, with many different opinions on how to address it. Understanding the size and characteristics of this population is an important part of any discussion or policy debate.
To know more about immigrants visit:
https://brainly.com/question/29998020
#SPJ11
PLSSSSS HELPPPP ITS MATH PLSSSS
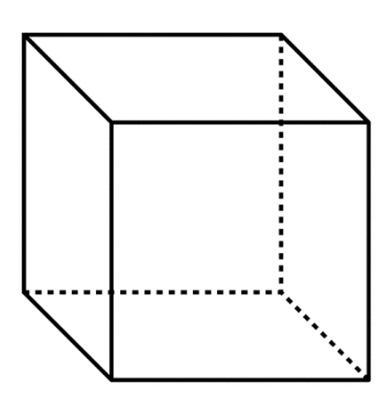
What 2-dimensional shapes do you see when you look at the Cube? Choose ALL that you see.
Squares
Rectangles
Triangles
Hexagons
Pentagons
Trapezoids
Answers
Answer: Squares
Step-by-step explanation:
The 2-dimensional shapes that one sees when one looks at the cube is the square. The cube consist of several squares.
It should be noted that the sides of a cube that is, its faces are squares. Also, the edges of the cube are straight lines while the corners which are the vertices are right angles.
four times The sum of 7 and w
Answers
Answer:
28
Step-by-step explanation:
\(7+7+7+7 = 14+7+7 = 21+7 = 28\)
O sino:
\(7*4 = 28\)
Construct a counterexample by model for the following invalid argument, and then explain exactly how your counterexample proves that the argument is invalid.
¼ of the hairs in Plato’s beard are gray. ¾ of the hairs in Aristotle’s beard are gray. So, Aristotle has a greater number of gray hairs in his beard than Plato does.
Answers
The given argument is invalid. It says that if one person has more gray hair in their beard than another person, then they have a higher percentage of gray hair in their beard.
The argument is invalid because it is possible for one person to have a higher percentage of gray hair in their beard but a lower number of gray hairs in total.One possible counterexample by model is:Suppose Plato has 200 hairs in his beard and 50 of them are gray. So, 1/4 of his hairs are gray. Now, let's suppose Aristotle has 400 hairs in his beard, and 300 of them are gray. So, 3/4 of his hairs are gray. Even though Plato has fewer gray hairs than Aristotle, his percentage of gray hairs is more significant (1/4) than Aristotle's (3/4).
Therefore, the given argument is invalid since Aristotle's beard contains more gray hairs in quantity, but Plato has a higher percentage of gray hair in his beard.
Learn more about argument here:
brainly.com/question/2645376
#SPJ11
The difference of two numbers is 16. The greater number is 4 times the smaller
number minus 5. Find the numbers.
Answers
After using the linear equation - The smaller number is 7, and the greater number will be 23.
what is the substitution method?
Mathematicians frequently use the substitution method to resolve an equation system. With this method, you solve the equation for the first variable first, and then plug the answer into the second equation.
what is a linear equation in two variables?
When an equation is written in the form axe + by + c=0 and the coefficients of x and y, i.e., a and b, respectively, are not equal to zero and the greater of the two numbers is four times the smaller number minus 5, that equation is said to be linear in two variables.
Let's assume that "x" is the smaller number, making "4x-5" the greater number. The requirement that the difference between the two numbers be 16 is also included.
thus,
4x - 5 - x = 16
3x -5 = 16
3x = 16 +5
3x =21
x = 21/3
x = 7
for the second number
4x-5
=4(7)-5
=28-5
=23
hence the smaller number is 7, and the greater number will be 23.
To learn more about linear equations visit:
https://brainly.com/question/2030026
#SPJ13
help ill mark brainliest

Answers
Answer:
y= 16, 64, 256, 1024
y/x= 16/2, 64/3, 256/4, 1024/5,
Step-by-step explanation:
This is just like any other equation, except instead of x being a number, it is an exponent. For example, when x equals 2, y equals 16 because y always equals four to the power of x. This applies to all of the parts in your table. when x equals 3, y equals 4^3 (4 times 4 times 4) which is 64, and when x equals 4, y equals 4^4 (4 times 4 times 4 times 4), which is 256.
For the y over x part that is just the value y, divided by the value x. For the first line on the table x equals 2, and we know y equals 16 (4^2 is 4 times 4, which is 16) so 16 divided by 2 is 8. That is the answer.
Hope this helps :)
Which of the following statement on the boundary value problem y" + xy = 0, y(0) = 0 and y(L) = 0 is NOT correct? (A) For A = 0, the only solution is the trivial solution y = 0. (B) For <0, the only solution is the trivial solution y = 0. (C) For X>0, the only solution is the trivial solution y = 0. (D) For A > 0, there exist nontrivial solutions when parameter A takes values ²² L2, n = 1, 2, 3, ...
Answers
Statement (C) "For X>0, the only solution is the trivial solution y = 0" is NOT correct.
Which statement regarding the boundary value problem y" + xy = 0, y(0) = 0 and y(L) = 0 is incorrect?The incorrect statement is (C) "For X>0, the only solution is the trivial solution y = 0." The given boundary value problem represents a second-order linear differential equation with boundary conditions.
The equation y" + xy = 0 is a special case of the Airy's equation. The boundary conditions y(0) = 0 and y(L) = 0 specify that the solution should satisfy these conditions at x = 0 and x = L.
Statement (C) claims that the only solution for x > 0 is the trivial solution y = 0. However, this is not correct. In fact, for A > 0, where A represents a parameter, there exist nontrivial solutions when the parameter A takes values λ², where λ = 1, 2, 3, and so on.
These nontrivial solutions can be expressed in terms of Airy functions, which are special functions that arise in various areas of physics and mathematics.
Therefore, statement (C) is the incorrect statement, as it incorrectly states that the only solution for x > 0 is the trivial solution y = 0, disregarding the existence of nontrivial solutions for certain values of the parameter A.
Learn more about boundary value problem
brainly.com/question/32558939
#SPJ11
Wildlife: Mallard Ducks and Canada Geese For mallard ducks and Canada geese, what percentage of nests are successful (at least one offspring survives)? Studies in Montana, Illinois, Wyoming, Utah, and California gave the following percentages of successful nests (Reference: The Wildlife Society Press, Washington, D.C.). x: Percentage success for mallard duck nests 56 85 52 13 39 y: Percentage success for Canada goose nests 24 53 60 69 18 (a) Use a calculator to verify that ??-245: ??2 = 14,755, 2y = 224; and (b) Use the results of part (a) to compute the sample mean, variance, and (c) Use the results of part (a) to compute the sample mean, variance, and ??? = 12,070. standard deviation for x, the percent of successful mallard nests. standard deviation for y, the percent of successful Canada goose nests.
Answers
(a) Using the given data, we can verify the calculations as follows: ∑x = 245, ∑x^2 = 14,755, ∑y = 224.
(b) To compute the sample mean, variance, and standard deviation for the percentage success of mallard duck nests (x), we use the formulas:
Sample Mean (x) = ∑x / n
Variance (s^2) = (∑x^2 - (n * x^2)) / (n - 1)
Standard Deviation (s) = √(s^2)
(c) Applying the formulas, we can compute the sample mean, variance, and standard deviation for x as follows:
Sample Mean (x) = 245 / 5 = 49
Variance (s^2) = (14,755 - (5 * 49^2)) / (5 - 1) = 4,285
Standard Deviation (s) = √(4,285) ≈ 65.5
Similarly, for the percentage success of Canada goose nests (y), the calculations can be done using the same formulas and the given values from part (a).
Learn more about standard deviation here: brainly.com/question/29808998
#SPJ11
identify the roots of the integrand to remove absolute values, then evaluate using the Fundamental Theorem of Calculus, Part 2. 195. ∫−24∣∣t2−2t−3∣∣dt
Answers
The integral ∫[-2, 4] |t^2 - 2t - 3| dt evaluates to -35/2. The roots of the integrand are t = 3 and t = -1, and the evaluation is done using the Fundamental Theorem of Calculus.
To evaluate the integral ∫[-2, 4] |t^2 - 2t - 3| dt using the Fundamental Theorem of Calculus, we need to identify the roots of the integrand to remove the absolute values.
Step 1: Find the roots of the integrand:
We have |t^2 - 2t - 3|. To find the roots, we set the expression inside the absolute value bars equal to zero and solve for t:
t^2 - 2t - 3 = 0
To factorize the quadratic equation, we look for two numbers that multiply to -3 and add up to -2. The factors are -3 and +1:
(t - 3)(t + 1) = 0
Setting each factor equal to zero gives us:
t - 3 = 0 --> t = 3
t + 1 = 0 --> t = -1
So, the roots of the integrand are t = 3 and t = -1.
Step 2: Evaluate the integral using the Fundamental Theorem of Calculus, Part 2:
We divide the interval [-2, 4] into three subintervals:
[-2, -1], [-1, 3], and [3, 4].
Within each subinterval, we have different expressions for the integrand:
For the subinterval [-2, -1]:
|t^2 - 2t - 3| = -(t^2 - 2t - 3) = -t^2 + 2t + 3
For the subinterval [-1, 3]:
|t^2 - 2t - 3| = t^2 - 2t - 3
For the subinterval [3, 4]:
|t^2 - 2t - 3| = -(t^2 - 2t - 3) = -t^2 + 2t + 3
Now, we can evaluate each part of the integral using the Fundamental Theorem of Calculus:
∫[-2, -1] -t^2 + 2t + 3 dt:
= [-t^3/3 + t^2 + 3t] from -2 to -1
= [(-(-1)^3/3 + (-1)^2 + 3(-1))] - [(-(-2)^3/3 + (-2)^2 + 3(-2))]
= [1/3 + 1 - 3] - [-8/3 + 4 - 6]
= [-5/3] - [-2/3]
= -5/3 + 2/3
= -3/3
= -1
∫[-1, 3] t^2 - 2t - 3 dt:
= [t^3/3 - t^2/2 - 3t] from -1 to 3
= [(3^3/3 - 3^2/2 - 3(3))] - [(-1^3/3 - (-1)^2/2 - 3(-1))]
= [27/3 - 9/2 - 9] - [-1/3 - 1/2 + 3]
= [9 - 9/2 - 9] - [-1/3 - 1/2 + 3]
= [9 - 18/2 - 18] - [-2/6 - 3/6 + 18/6]
= [9 - 9 - 18] - [13/6]
= -18 - 13/6
= -36/2 - 13/6
= -72/6 - 13/6
= -85/6
∫[3, 4] -t^2 + 2t + 3 dt:
= [-t^3/3 + t^2 + 3t] from 3 to 4
= [-(4^3/3) + 4^2 + 3(4)] - [-(3^3/3) + 3^2 + 3(3)]
= [-64/3 + 16 + 12] - [-27/3 + 9 + 9]
= [-64/3 + 28] - [-9 + 18]
= [-64/3 + 84/3] - [9]
= [20/3] - [9]
= 20/3 - 27/3
= -7/3
Finally, we sum up the results for each subinterval to get the overall integral:
∫[-2, 4] |t^2 - 2t - 3| dt = ∫[-2, -1] -t^2 + 2t + 3 dt + ∫[-1, 3] t^2 - 2t - 3 dt + ∫[3, 4] -t^2 + 2t + 3 dt
= -1 + (-85/6) + (-7/3)
= -1 - (85/6) - (7/3)
= -6/6 - (85/6) - (14/6)
= -(6 + 85 + 14)/6
= -105/6
= -35/2
Therefore, the value of the integral ∫[-2, 4] |t^2 - 2t - 3| dt is -35/2.
Learn more about Fundamental Theorem of Calculus here: brainly.com/question/30761130
#SPJ11
The radius of a circle is 6 inches. What is the circle's area?
Use 3.14 for'a.
square inches
Submit
Answers
Answer:
113.04 in^2
Step-by-step explanation:
6^2×3.14=113.04 in^2
Answer:
113.04
Step-by-step explanation:
3.14 x (6x6) = 113.04
when running a half marathon (13.1 miles), it took noah 8 minutes to run from mile marker 1 to mile marker 2, and 19 minutes to run from mile marker 2 to mile marker 4. how long did it take noah to run from mile marker 1 to mile marker 4?
Answers
Answer:
27
Step-by-step explanation:
Helppp this is a Algebra question

Answers
(*) multiply sign
(/) division sign
Derek drives 125 miles in 2 1/2 hours. At the same rate, how far will he be able to travel in 6 hours?
Answers
Answer:
300 miles
Step-by-step explanation:
125 ÷ 2.5 = 50 miles per hour
50 x 6 = 300 miles
A textbook store sold a combined total of 240 chemistry and history textbooks in a week. The number of chemistry textbooks sold
was two times the number of history textbooks sold. How many textbooks of each type were sold?
Answers
Answer:
160 chemistry books and 80 history books
Step-by-step explanation:
C=chemistry books sold, H=history books sold
C=2H
C+H=240, 3H=240, H=80, C=160
the expected value for a binomial probability distribution is group of answer choices e(x) = pn(1 - n) e(x) = p(1 - p) e(x) = np e(x) = np(1 - p)
Answers
The correct answer is e(x) = np. The expected value for a binomial probability distribution is given by the formula e(x) = np, where n represents the number of trials and p represents the probability of success in each trial.
The expected value is a measure of the average or mean outcome of a binomial experiment. It represents the number of successful outcomes one would expect on average over a large number of trials.
The formula e(x) = np arises from the fact that the expected value of a binomial distribution is the product of the number of trials (n) and the probability of success (p) in each trial. This is because in a binomial experiment, the probability of success remains constant for each trial.
Therefore, to calculate the expected value of a binomial probability distribution, we multiply the number of trials by the probability of success in each trial, resulting in e(x) = np.
Learn more about binomial here:
https://brainly.com/question/30339327
#SPJ11
Evaluate the following expression for x = 1 and y = -3.
3yºx+x-y
Answers
Answer:
8
Step-by-step explanation:
yº (in words, 'y to the power zero') is simply 1. We then have
3yºx+x-y = 3(1) + 2x - y = 3 + 2x - y.
Substituting 1 for x and -3 for y, we get the expression value:
3 + 2 - (-3) = 8
Kira's foot is 11 inches long. Use the ruler below the measure her hand. How much is long kristi's foot than her hand?

Answers
4 inches ⭐️
Suppose we want to choose 6 colors, without replacement, from 14 distinct colors.
Answers
We want to choose 6 colors without replacement from a set of 14 distinct colors. We need to determine the number of possible combinations.
To find the number of combinations, we can use the concept of combinations without replacement. The formula for combinations is given by:
C(n, r) = n! / (r!(n - r)!)
Where n represents the total number of items and r represents the number of items to be chosen.
In this case, we have 14 distinct colors and we want to choose 6 colors. Plugging the values into the formula, we get:
C(14, 6) = 14! / (6!(14 - 6)!)
Simplifying the expression:
C(14, 6) = 14! / (6!8!)
Using factorials:
C(14, 6) = (14 * 13 * 12 * 11 * 10 * 9) / (6 * 5 * 4 * 3 * 2 * 1)
Calculating the result:
C(14, 6) = 3003
Therefore, there are 3003 possible combinations of 6 colors that can be chosen from 14 distinct colors without replacement.
Learn more about replacement here : brainly.com/question/31948375
#SPJ11
(brainliest) please help!!

Answers
Answer:
(-1, 3)
Step-by-step explanation:
Ben bought a digital camera for $90 the tax rate is 6% which proportion can be used to find the amount of tax ben will pay
Answers
Answer:
x/90=6/100
Hope this helps :)
Please do all or as much as you can!!!





Answers
Answer:
see explanation
Step-by-step explanation:
1
the 2 legs of the triangle are congruent then the triangle is isosceles.
the segment from the vertex to the base is a perpendicular bisector, then
x = 6
using Pythagoras' identity in the lower right triangle to calculate the leg, which is the hypotenuse h
h² = 6² + 8² = 36 + 64 = 100 ( take square root of both sides )
h = \(\sqrt{100}\) = 10
then
perimeter = 10 + 10 + 6 + 6 = 32
---------------------------------------------------------
2
Δ DFE and Δ HFG are similar by the AA postulate , then corresponding angles are congruent, so
∠ E = ∠ G , that is
6x - 4 = 5x + 4 ( subtract 5x from both sides )
x - 4 = 4 ( add 4 to both sides )
x = 8
then
∠ E = 6x - 4 = 6(8) - 4 = 48 - 4 = 44°
------------------------------------------------------------------
3
line P bisects XZ , then WX = 5
Δ XYZ is isosceles with XY = ZY
since perimeter = 36 then
XY = (36 - XZ) ÷ 2 = (36 - 10) ÷ 2 = 26 ÷ 2 = 13
using Pythagoras' identity in right triangle WXY
WY² + WX² = XY²
WY² + 5² = 13²
WY² + 25 = 169 ( subtract 25 from both sides )
WY² = 144 ( take square root of both sides )
WY = \(\sqrt{144}\) = 12
-----------------------------------------------------------------------------
4
∠ ACB and ∠ BCD are a linear pair and sum to 180°
∠ ACB + 120° = 180° ( subtract 120° from both sides )
∠ ACB = 60°
since AC = BC then Δ ABC is isosceles with base angles congruent
∠ B = ∠ A
the exterior angle of a triangle is equal to the sum of the 2 opposite interior angles.
∠ BCD is an exterior angle of the triangle , so
∠ A + ∠ B = 120° ( since ∠ A = ∠ B ) , then
2 ∠ B = 120° ( divide both sides by 2 )
∠ B = 60°
-----------------------------------------------------------------------
5
the exterior angle of a triangle is equal to the sum of the 2 opposite interior angles.
∠ XYZ is an exterior angle of the triangle , then
15x - 18 = 5x + 2 + 8x + 4
15x - 18 = 13x + 6 ( subtract 13x from both sides )
2x - 18 = 6 ( add 18 to both sides )
2x = 24 ( divide both sides by 2 )
x = 12
when choosing between one-tailed and two-tailed tests, group of answer choices use a two-tailed test only if you have a convincing reason for not predicting a direction. use the one that is most likely to produce significant results. use a one-tailed test only if you have a convincing reason for predicting the direction. always use two-tailed tests.
Answers
The recommended approach when choosing between one-tailed and two-tailed tests is to use a two-tailed test only.
The choice between a one-tailed or two-tailed test should be based on the research hypothesis and the specific question being investigated.
If you have a convincing reason for not predicting a direction, and use the one that is most likely to produce significant results.
If the research hypothesis or question does not make a clear directional prediction, then a two-tailed test would be appropriate.
This is because a two-tailed test will consider the possibility of significant results in both directions of the distribution.
And is more conservative in its estimation of significance.
If the research hypothesis or question does make a clear directional prediction, then a one-tailed test would be appropriate.
This is because a one-tailed test will only consider the possibility of significant results in one direction of the distribution.
And is more powerful in detecting significant results in that specific direction.
Therefore, the answer is to use a two-tailed test only if you have a convincing reason for not predicting a direction, and use the one that is most likely to produce significant results.
Learn more about tailed test here
brainly.com/question/17204018
#SPJ4
A building casts a shadow 47 feet long. At the same time, a 38‐foot‐tall flagpole casts a shadow 9.4 feet long. What is the height of the building?
Answers
Answer: the answer would be 75.6 i think, sorry if that's wrong
Step-by-step explanation:
38-9.4=28.6
28.6+47=75.6
PLS HELP WILL MARK YOU BRAINLIEST! NO FAKE ANSWERS! An inheritance of 2 Million was given to a young professional by his parents. He invested the entire amount in real estate, mutual funds, government bonds, and crytocurrencies.

Answers
Answer:
a) 17.5%
b) $150,000
c) 27°
Step-by-step explanation:
Angles around a point add up to 360°.
Therefore, to find the percentage of the portion of the pie chart, divide the degree of the portion by 360° and multiply by 100%
Assuming that Real Estate is half of the circle, and Mutual Funds are a quarter of the circle.
a) Government Bonds = (63° ÷ 360°) x 100% = 17.5%
b) Crypto Currency = 90° - 63° = 27°
Therefore, (27° ÷ 360°) x 100% = 7.5%
7.5% of $2,000,000 = 0.075 x $2,000,000 = $150,000
c) Crypto Currency = 90° - 63° = 27°
#a
Find percentage (whole is 360°)
63/360×1000.175(100)17.5%#2
Angle of crypto=180-(90+63)=180-153=27°
Percentage:-
27/360×1000.075(100)7.5%Total
2M(0.075)0.15M150K#c
Found in second part
what would the answer be for 3-4(3+2y)+7
Answers
Explanation:
Step-by-step explanation:
Step 1:
\(3-4(3+2y)+7\)
Step 2:
\( = 3 - 12 - 8y + 7\)
Step 3:
\( = 10 - 12 - 8y\)
Step 4:
\( = -2 - 8y\)
hope it helped you:)
two people are in a boat that is capable of a maximum speed of 5 kilometers per hour in still water, and wish to cross a river 1 kilometer wide to a point directly across from their starting point. if the speed of the water in the river is 5 kilometers per hour, how much time is required for the crossing?
Answers
This is approximately 0.283 hours, or 17 minutes. Therefore, it will take the boat approximately 17 minutes to cross the river.
The key to solving this problem is to understand the concept of relative velocity. In this case, the boat's speed relative to the water is 5 km/hr, and the water's speed relative to the shore is also 5 km/hr. Therefore, the boat's speed relative to the shore is the vector sum of these two velocities, which is 0 km/hr. This means that the boat will not make any progress toward the other side of the river unless it angles its course slightly upstream.
To determine the angle required, we need to use trigonometry. Let θ be the angle the boat makes with the direction perpendicular to the river. Then sin θ = 5/5 = 1, so θ = 45 degrees. This means that the boat needs to head upstream at a 45-degree angle to make progress across the river.
Now we can use the Pythagorean theorem to find the distance the boat travels:
d = √(1² + 1²) = √(2) km
Since the boat's speed relative to the shore is 0 km/hr, the time required for the crossing is simply the distance divided by the boat's speed relative to the water:
t = d / 5 = √(2) / 5 hours
This is approximately 0.283 hours or 17 minutes. Therefore, it will take the boat approximately 17 minutes to cross the river.
Learn more about trigonometry here:
https://brainly.com/question/12068045
#SPJ11
g = c + x , solve for x
Answers
Answer:
Step-by-step explanation:
g = c + x
g - c = x
Can somebody help me with this problem i need great help and 10 pts with be giving

Answers
Answer:
The answer is -3<x≤2
simple 9th grade math

Answers
Answer:
-1078
Step-by-step explanation:
To find the nth term in an arithmetic sequence we use the following formula
aₙ=a₁+(n-1)*d
Where a₁ is the first time, and d is the common difference (in this case -20)
So we have
2+(55-1)*-20
2+(54)*-20
2-1080
-1078
please help me with this slope problem! :) (brainliest)

Answers
Answer:
Plot these points
(1,935)
(2,870)
(3,805)
(4,740)
(5,675)
Slope= -65
y intercept = 1000
and what it's saying is that we travel at a speed of 65 units an hour and we start 1000 miles away
Step-by-step explanation:
Just graph these points which you can get by plugging in the numbers
1000-65= 935
(1,935)
1000-65*2=870
(2,870)
1000-65*3= 805
(3,805)
1000-65*4=740
(4,740)
1000-65*5= 675
(5,675)
B:
y= mx+b where m is the slope and B is the y intercept
we can re write the equation as follows
-65x+1000
It's pretty clear that -65 is the slope and 1000 is the y intercept
